2. 重庆大学 输配电装备及系统安全与 新技术国家重点实验室, 重庆 400044
2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China
输电线路故障测距装置根据不同的故障特征测定故障点位置,对及时修复线路故障和保证电力系统可靠供电有重要意义。目前输电线路的故障测距主要采用行波法和故障分析法,其中,基于单端阻抗法的故障分析测距原理利用单侧系统信息、不受通信条件约束,具有简单、经济、易于实现等特性[1-3]。针对系统运行方式变化以及过渡电阻等因素对单端阻抗法故障测距精度的影响,国内外学者提出了不同的改进策略以提高测距的精确性。文献[4]提出的集成测量阻抗法与行波法的测距方法有效提高了故障测距的准确性;文献[5]利用故障后的稳态量及暂态量进行测距计算,提出了一种估算对侧信息的单端故障测距方法;文献[6]在故障电压瞬时值过零点时刻计算测量阻抗,提出一种新型单端阻抗故障测距方法。
柔性直流输电由于具有无换相失败、可向无源系统供电、独立调节有功与无功功率、谐波水平低等优点,在新能源并网、区域电网互联等领域具有明显的优势[7]。在基于柔性直流输电的交直流联网方式下,系统中的故障特征量受到换流器控制和电力电子元件非线性的影响[8-9],其传变特征与传统交流系统相比表现出很大不同。现有的单端故障测距原理及其研究均以传统交流系统的工频故障特征量为条件,因此在交直流互联系统中可能产生一定的测距误差。目前针对直流馈入下交流系统理论研究主要集中在常规直流交流侧故障分析、柔直系统交流侧不对称故障穿越控制和故障仿真等方面[10-13],针对常规直流或柔性直流馈入下交流电网输电线路故障测距的研究还鲜有文献报道。
针对柔直馈入下交流输电线路单端故障测距可能产生的影响,考虑了柔直换流器在电网故障期间的不同运行状态,通过对柔直换流器在保护未启动、限流和闭锁情况下交流侧短路电流的分析与推导,分析了柔直馈入引起单端故障测距精度误差的特征及原因,并通过仿真验证了分析的正确性。
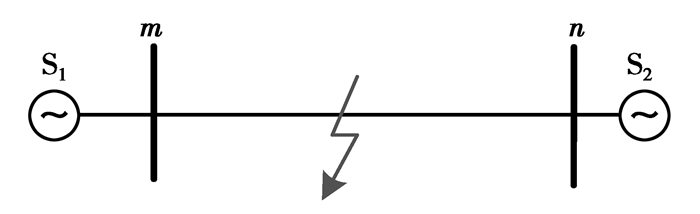
1 输电线路单端阻抗法测距单端阻抗法测距是基于线路一端测量得到的故障电压、电流和系统参数,通过测距算法计算得出故障点的距离位置[14]。图 1为双端交流系统中发生短路故障时的故障示意图,m侧和n侧分别代表两侧交流系统,S1和S2分别代表m侧和n侧系统等值电压源,ZS1和ZS2分别代表两侧系统阻抗,在m端处的测量阻抗可表示为
| $ {Z_m} = {\rm{ }}\frac{{{{\dot U}_m}}}{{{{\dot I}_m}}} = z{D_{m{\rm{f}}}} + \frac{{{{\dot I}_{\rm{f}}}}}{{{{\dot I}_{\rm{m}}}}}{R_{\rm{f}}} = z{D_{m{\rm{f}}}} + \Delta Z, $ | (1) |
|
图 1 交流线路故障示意图 Figure 1 Diagram of AC transmission line fault |
式中:Zm为m端测量阻抗值;
根据叠加原理,m端测量电流可以由负荷电流分量
| $ {{\dot I}_m} = {{\dot I}_{m{\rm{H}}}} + {{\dot I}_{m{\rm{g}}}} = {{\dot I}_{m{\rm{H}}}} + \dot K{{\dot I}_{\rm{f}}}, $ | (2) |
| $ \dot K = \frac{{{Z_{{\rm{S}}2}} + z{D_L}-z{D_{m{\rm{f}}}}}}{{{Z_{{\rm{S1}}}} + {Z_{{\rm{S}}2}} + z{D_L}}} = K{{\rm{e}}^{j\gamma }}, $ | (3) |
式中:
传统双端交流输电系统发生短路时,电流分布系数相角γ值较小,一般不超过10°,可认为故障点电流与线路m端故障分量
结合式(2) 和(3),可将式(1) 中m端测量阻抗表示为
| $ {Z_m} = z{D_{m{\rm{f}}}} + \left( {\frac{{{R_f}}}{K}} \right)\frac{{{{\dot I}_{m{\rm{g}}}}}}{{{{\dot I}_m}}} 。$ | (4) |
对式(4) 左右两侧取实部和虚部得到
| $ X{D_{m{\rm{F}}}} = {X_m}-\frac{{{R_{\rm{f}}}}}{K} \cdot b, $ | (5) |
| $ R{D_{m{\rm{F}}}} = {R_m}-\frac{{{R_{\rm{f}}}}}{K} \cdot a, $ | (6) |
式中:
| $ {\rm{tan}}{\varphi _L} = X/R, $ | (7) |
结合式(4)~式(7) 得到
| $ {D_{m{\rm{f}}}} = {\rm{ }}\frac{{{X_m}}}{X}{\rm{ }}- {\rm{ }}\frac{{{R_m}{\rm{tan}}{\varphi _L}- {X_m}}}{{X(a\;{\rm{tan}}{\varphi _L}- b)}} = \frac{{{X_m}}}{X} - \frac{{{R_m}{\rm{tan}}{\varphi _L} - {X_m}}}{{X\left( {{\mathop{\rm Im}\nolimits} \left[{\frac{{{{\dot I}_{m{\rm{g}}}}}}{{{{\dot I}_m}}}} \right]{\rm{tan}}{\varphi _L} - {\mathop{\rm Re}\nolimits} \left[{\frac{{{{\dot I}_{m{\rm{g}}}}}}{{{{\dot I}_m}}}} \right]} \right)}}, $ | (8) |
式中Dmf为单端故障测距结果,由于Dmf不含过渡电阻Rf,因此测距结果能够排除过渡电阻的影响。
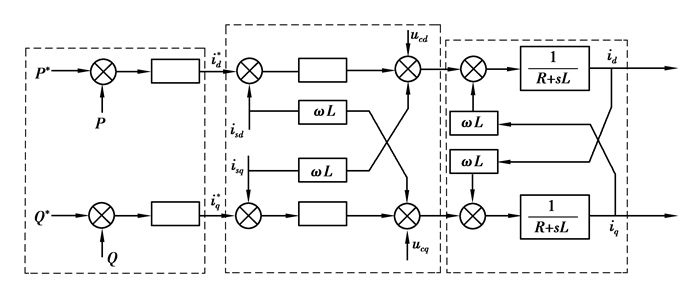
2 柔直交流侧故障特征分析柔性直流输电工程广泛采用两电平和模块化多电平换流器拓扑结构,但是不论采用何种结构,换流器控制方式都是类似的。柔直换流器一般采用基于内环电流控制器和外环功率控制器的矢量控制方法。外环可以采用有功功率、无功功率、直流电压、交流电压等控制策略的组合[16]。在同步d-q旋转坐标系下换流器矢量控制原理结构图如图 2所示。
|
图 2 换流器矢量控制结构图 Figure 2 Vector control structure of converter |
矢量控制策略是在d-q坐标系下对换流器进行控制,内环电流控制器通过调节换流器输出电压,对d、q轴电流分量进行控制,使其快速跟踪指令值;外环控制器根据有功功率、无功功率和直流电压等指令值,计算内环电流控制器的d、q电流分量的指令值,控制器采用电网d轴定向方式[17]。电流内环经解耦控制后简化结构如图 3所示。

|
图 3 电流内环简化结构图 Figure 3 Simplified block diagram of inner current loop |
忽略实际数字控制系统中的信号采样及滤波延时、换流器的开关延时等因素。此时,d轴电流环的闭环传递函数为
| $ G\left( s \right) = {\rm{ }}\frac{{{i_d}}}{{i_d^*}} = \frac{{{K_{\rm{p}}}s + {K_i}}}{{L{s^2} + (R + {K_{\rm{p}}})s + {K_i}}}, $ | (9) |
式中:
式(9) 经零极点相消后,电流控制闭环传递函数可简化为
| $ G\left( s \right) = {\rm{ }}\frac{{{K_{\rm{p}}}}}{{{K_{\rm{p}}} + Ls}}{\rm{ }} = \frac{1}{{1 + \frac{s}{{{\omega _{\rm{c}}}}}}}, $ | (10) |
式中,ωc=Kp/L。
此时,电流内环为一阶惯性环节。当开关频率足够高,电流内环具有较快的响应速度,可忽略暂态过程,d轴输出电流id等于指令值
| $ \left\{ \begin{array}{l} i_d^* = {\rm{ }}\frac{{{P^*}}}{{1.5{U_{\rm{c}}}}}, \\ i_q^* =-\frac{{{Q^*}}}{{1.5{U_{\rm{c}}}}}, \end{array} \right. $ | (11) |
式中:P*和Q*分别为换流器有功功率和无功功率指令值; Uc为换流器交流母线出口侧电压。
考虑到柔性直流输电系统中换流阀过载能力有限,系统发生故障时产生的过流可能导致换流阀IGBT元件的损坏,可以通过配置换流器限流保护或闭锁保护来保障柔性直流换流器的安全运行[18]。根据柔直交流侧故障严重程度和换流器保护配置情况,交流侧发生故障时,柔直换流器可能运行于以下3种模式:换流器保护未启动、换流器限流保护、换流器闭锁。
2.1 换流器保护未启动当柔直交流侧系统发生远端或高阻接地故障时,且柔直换流器输出短路电流未达到换流器电流限幅控制限值imax或闭锁限值,换流器输出三相短路电流为
| $ \left\{ \begin{array}{l} {i_{{\rm{c}}a1}}\left( t \right) = {I_m}{\rm{cos}}\left( {{\omega _1}t + {\theta _1} + \varphi } \right), \\ {i_{{\rm{c}}b1}}\left( t \right) = {I_m}{\rm{cos}}\left( {{\omega _1}t + {\theta _1}-\frac{{2\pi }}{3} + \varphi } \right), \\ {i_{{\rm{c}}c1}}\left( t \right) = {I_m}{\rm{cos}}\left( {{\omega _1}t + {\theta _1} + \frac{{2\pi }}{3} + \varphi } \right), \end{array} \right. $ | (12) |
式中,θ1为a相电流初相角。
| $ {I_m} = \frac{2}{{3{U_{\rm{c}}}}}\sqrt {{{({P^*})}^2} + {{({Q^*})}^2}}, $ | (13) |
| $ \varphi =-{\rm{arctan}}({Q^*}/{P^*})。$ | (14) |
当换流器限流或闭锁保护未启动,短路电流幅值和相位由换流器有功功率指令、无功功率指令和换流器交流侧电压跌落系数决定。
2.2 换流器限流保护当柔直换流器配置限流保护且柔直交流侧系统电压幅值跌落较深,导致换流器输出短路电流幅值达到限流设定幅值imax (该电流幅值一般为交流侧额定输出电流的1~2倍,文中取imax=1.2 pu)。此时,换流器通过限制内环电流有功分量和无功分量的参考值将交流输出电流保持在安全幅值范围内[19-20]。经限流控制后内环电流控制器d,q电流分量
| $ i_{d1}^* = {\rm{ }}\frac{{{i_{{\rm{max}}}}}}{i}i_d^* = \alpha i_d^*, $ | (15) |
| $ {i_{{\rm{max}}}} = \sqrt {{{(i_{d1}^*)}^2} + {{(i_{q1}^*)}^2}}, $ | (16) |
式中:α为电流限制系数;i为换流器输出短路电流幅值大小。
此时,换流器侧输出三相短路电流可表示为
| $ \left\{ \begin{array}{l} {i_{ca1}}\left( t \right) = {i_{{\rm{max}}}}{\rm{cos}}({\omega _1}t + {\theta _1} + \varphi ), \\ {i_{cb1}}\left( t \right) = {i_{{\rm{max}}}}{\rm{cos}}\left( {{\omega _1}t + {\theta _1}-\frac{{2\pi }}{3} + \varphi } \right), \\ {i_{cc1}}\left( t \right) = {i_{{\rm{max}}}}{\rm{cos}}\left( {{\omega _1}t + {\theta _1} + {\rm{ }}\frac{{2\pi }}{3} + \varphi } \right), \end{array} \right. $ | (17) |
式中:imax为换流器限流设定幅值,φ=-arctan(Q*/P*)。换流器侧输出电流幅值维持在限幅指令值imax,短路电流初相角受换流器无功控制指令和最大无功输出能力影响。
2.3 换流器闭锁当交流线路发生永久性或近端严重短路故障,需要通过交流断路器切除故障,而断路器的响应速度一般需要60~100 ms的响应时间,并不能及时保护IGBT元件,因此可通过闭锁IGBT来迅速隔离短路电流的影响[21]。此时,换流器IGBT器件关断,换流器在交流侧故障前后的等效电路如图 4所示,由于直流侧不能通过反向二极管向故障点注入电流,换流器闭锁后不再向交流系统输出短路电流。

|
图 4 换流器等效电路图 Figure 4 Equivalent circuit diagram of converter |
柔直交流侧系统发生短路故障后,交流侧短路电流特征呈现不同的变化规律,如表 1所示。
| 表 1 3种情况下换流器特征对比 Table 1 Characteristic comparison under three conditions |
当电网发生不对称故障时,负序电流分量会严重影响控制器的性能并危及换流装置的安全,因此柔直换流器级控制保护层一般采用负序电流抑制控制策略[22]。此时的短路电流与对称故障时类似。
3 柔直交流侧单端故障测距性能影响分析换流器在交流侧不同严重程度故障下具有不同的故障特征,当柔直换流器闭锁时,换流器交流侧无短路电流,此时,故障测距方法已不适用。下面分析换流器在保护未启动和限流保护启动条件下的单端故障测距性能。
3.1 换流器保护未启动结合测量阻抗表达式,式(8) 的测量阻抗可以表示为
| $ {D_{m{\rm{F}}}} = \frac{{{\rm{Im}}\left[{\frac{{{{\dot U}_m}}}{{{I_m}\angle \varphi }}} \right]{\rm{ }}}}{X} - \frac{{{\rm{Re}}\left[{\frac{{{{\dot U}_m}}}{{{I_m}\angle \varphi }}} \right]{\rm{tan}}{\varphi _L} - {\rm{Im}}\left[{\frac{{{{\dot U}_m}}}{{{I_m}\angle \varphi }}} \right]}}{{X\left( {{\rm{Im}}\left[{\frac{{{{\dot I}_{m{\rm{g}}}}}}{{{I_m}\angle \varphi }}} \right]{\rm{tan}}{\varphi _L} - {\rm{Re}}\left[{\frac{{{{\dot I}_{m{\rm{g}}}}}}{{{I_m}\angle \varphi }}} \right]} \right)}}, $ | (18) |
式中,测距结果DmF受交流侧短路电流幅值Im、相角φ和电压跌落大小
在非深度跌落条件下换流器限流保护未启动,随着故障期间无功控制指令值Q*变化,柔直交流侧短路电流幅值和相位随之改变,进而影响故障测距结果。
3.2 换流器限流保护状态当换流器交流侧输出短路电流达到控制器限流幅值后,随着故障点电压跌落深度的增大,换流器输出短路电流
| $ {D_{m{\rm{F}}}} = \frac{{{\rm{Im}}\left[{\frac{{{{\dot U}_m}}}{{{i_{\max }}\;\angle \varphi }}} \right]{\rm{ }}}}{X} - \frac{{{\rm{Re}}\left[{\frac{{{{\dot U}_m}}}{{{i_{\max }}\;\angle \varphi }}} \right]{\rm{tan}}{\varphi _L} - {\rm{Im}}\left[{\frac{{{{\dot U}_m}}}{{{i_{\mathit{max}}}\;\angle \varphi }}} \right]}}{{X\left( {{\rm{Im}}\left[{\frac{{{{\dot I}_{m{\rm{g}}}}}}{{{i_{\max }}\;\angle \varphi }}} \right]{\rm{tan}}{\varphi _L} - {\rm{Re}}\left[{\frac{{{{\dot I}_{m{\rm{g}}}}}}{{{i_{\max }}\;\angle \varphi }}} \right]} \right)}}, $ | (19) |
式中,测距结果DmF受电压跌落大小
在深度电压跌落条件下,换流器输出短路电流幅值维持在imax,而电流相角φ仍随无功指令变化而变化,即改变故障期间无功控制指令会引起故障测距结果的改变。
4 仿真验证仿真系统如图 5所示,柔性直流换流器额定容量为1 200 MVA,直流系统电压±320 kV,换流器阀侧交流母线电压220 kV,换流变压器变比220 kV/242 kV,交流系统频率50 Hz,交流输电线路长度200 km,线路单位长度正序电阻0.015 37 Ω/km,零序电阻0.046 12 Ω/km,正序电感0.885 8 mH/km,零序电感2.567 4 mH/km,正序电容13.065 nF/km,零序电容4.355 nF/km。整流侧换流器采用定直流电压和无功控制,逆变侧换流器采用定有功功率和无功功率控制方式。

|
图 5 柔性直流馈入下交流侧故障等效电路图 Figure 5 Equivalent circuit of AC side fault under Flexible HVDC infeed |
稳态运行时柔直换流器传输有功功率600 MW,无功功率指令为零。t=4 s时,分别在距换流器交流侧20、40、60、100 km处发生三相永久性短路,过渡电阻均为100 Ω。此时,柔直输出短路电流未达到设定幅值,换流器保护不启动。由式(8) 可以计算得到故障位置如表 2所示,得到的单端故障测距误差均在2%,基本反映了真实位置。
| 表 2 换流器侧故障测距结果 Table 2 Fault location results in converter side |
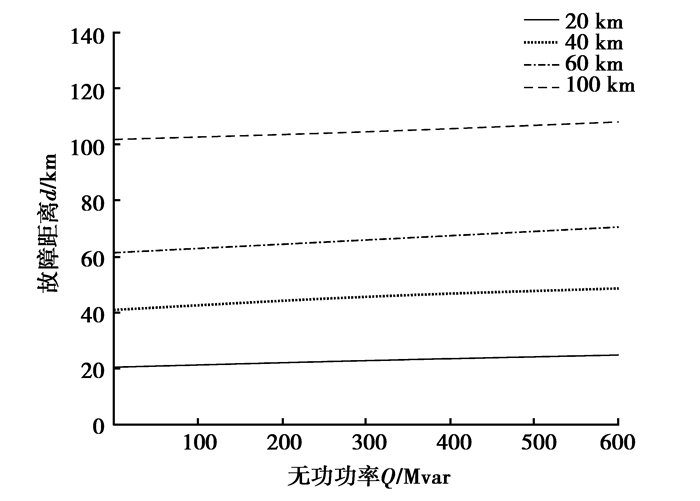
在不同故障距离,通过改变换流器故障期间无功控制量,故障测距结果的变化如图 6所示。表 3给出了换流器在故障期间不发无功、发出300 Mvar和600 Mvar无功功率控制指令下的测距结果。
|
图 6 不同无功功率指令下故障测距结果变化 Figure 6 Variation of fault location results under different reactive power command |
| 表 3 不同无功指令下换流器侧故障测距结果 Table 3 Fault location results in converter side under different reactive power command |
从图 6和表 3分析可知,换流器无功控制指令为零时故障测距误差均维持在2%左右,随着换流器故障期间无功控制指令值的增大,单端测距误差逐渐有所增大。
4.2 换流器限流保护状态稳态运行时柔直换流器传输有功功率600 MW,在t=4 s时距换流器交流侧不同距离发生三相短路故障,设置过渡电阻1 Ω,此时,换流器输出电流达到短路限流幅值imax,换流器交流侧故障测距结果如表 4所示,在测量结果均远大于实际故障距离,测距误差均在30%以上。
| 表 4 换流器侧故障测距结果 Table 4 Fault location results in converter side |
在不同故障距离,通过改变换流器无功控制量,故障测距结果的变化如图 7所示。表 5给出了换流器在故障期间不发无功、发出300 Mvar和600 Mvar无功功率控制指令下的测距结果。

|
图 7 不同无功功率指令下故障测距结果 Figure 7 Variation of fault location results under different reactive power command |
| 表 5 不同无功指令下换流器侧故障测距结果 Table 5 Fault location results in converter side under different reactive power command |
从图 7和表 5分析可知,在换流器达到限流条件时,测距结果已不能正确反映实际故障距离,柔直交流侧测距误差依然随着无功控制量的增大而增大。由以上不同故障测距结果算例分析可得,在柔直换流器限流或闭锁保护未启动时,柔直交流侧故障测距结果尚能反映实际故障距离,但测量误差随无功控制量增大而增大;在柔直限流条件启动时,柔直交流侧测距结果已经不能反映实际故障距离,测距公式几乎不适用。由于柔直换流站交流侧故障特征及其对故障测距结果主要受故障期间换流站控制方式的影响,受直流侧线路类型和长度等因素的影响较小,因此,文中的分析结论对于直流侧采用直流电缆或架空线路(以及它们的组合)的柔直馈入系统都具有一定适用性。
5 结论针对柔性直流馈入下交流输电线路单端故障测距的性能,分析并揭示了柔直换流器在不同暂态运行状态下的故障特征量变化规律及其对单端故障测距的影响,所得结论如下:
1) 柔性直流换流器输出故障特性与控制器限流或闭锁保护配置情况有关,受换流器交流侧电压跌落系数和换流器无功功率指令的影响。
2) 柔直换流器保护未启动时,柔直交流侧故障测距误差较小,但测量误差随故障期间换流器无功控制量增大而增大。
3) 在柔直换流器限流保护作用下,单端故障测距结果误差较大,不能反映实际故障距离;而在柔直换流器闭锁启动时,单端故障测距已不适用。
| [1] | Abe M, Otsuzuki N, Emura T, et al. Development of a new fault location system for multi-terminal single transmission lines[J]. IEEE Transactions on Power Delivery, 1995, 10(1): 159–169. DOI:10.1109/61.368402 |
| [2] | Kezunovic M. Smart fault location for smart grids[J]. IEEE Transactions on Smart Grid, 2011, 2(1): 11–22. DOI:10.1109/TSG.2011.2118774 |
| [3] |
李强, 王银乐.
高压输电线路的故障测距方法[J]. 电力系统保护与控制, 2009, 37(23): 192–197.
LI Qiang, WANG Yinle. Fault location methods for high voltage power transmission lines[J]. Power System Protection and Control, 2009, 37(23): 192–197. DOI:10.3969/j.issn.1674-3415.2009.23.050 (in Chinese) |
| [4] |
郑秀玉, 丁坚勇, 黄娜.
输电线路单端故障定位的阻抗-行波组合算法[J]. 电力系统保护与控制, 2010, 38(6): 18–21.
ZHENG Xiuyu, DING Jianyong, HUANG Na. Impedance-traveling wave assembled algorithm of one-terminal fault location for transmission lines[J]. Power System Protection and Control, 2010, 38(6): 18–21. DOI:10.7667/j.issn.1674-3415.2010.06.004 (in Chinese) |
| [5] |
冉伊, 周步祥, 杨植雅, 等.
一种估算对侧信息的配电网单端故障测距方法[J]. 电力系统保护与控制, 2014, 42(18): 25–31.
RAN Yi, ZHOU Buxiang, YANG Zhiya, et al. A method of single ended fault location for distribution network based on estimated contralateral information[J]. Power System Protection and Control, 2014, 42(18): 25–31. DOI:10.7667/j.issn.1674-3415.2014.18.005 (in Chinese) |
| [6] |
王宾, 董新洲, 薄志谦.
特高压长线路单端阻抗法单相接地故障测距[J]. 电力系统自动化, 2008, 32(14): 25–29.
WANG Bin, DONG Xinzhou, BO Zhiqian. An Impedance Fault Location Algorithm for UHV Long Transmission Lines with Single-line-to-ground Faults[J]. Automation of Electric Power Systems, 2008, 32(14): 25–29. DOI:10.3321/j.issn:1000-1026.2008.14.006 (in Chinese) |
| [7] | Debnath S, Qin J, Bahrani B, et al. Operation, control, and applications of the modular multilevel converter:a review[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 37–53. DOI:10.1109/TPEL.2014.2309937 |
| [8] | Bianchi F D, Egea-alvarez A, Junyent-ferré A, et al. Optimal control of voltage source converters under power system faults[J]. Control Engineering Practice, 2012, 20(5): 539–546. DOI:10.1016/j.conengprac.2012.01.009 |
| [9] | Shi X, Wang Z, Liu B, et al. Characteristic investigation and control of a modular multilevel converter-based HVDC system under single-line-to-ground fault conditions[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 408–421. DOI:10.1109/TPEL.2014.2323360 |
| [10] |
马世强, 余利霞, 郑连清.
MMC-HVDC交流侧不对称故障特性分析与保护策略[J]. 华北电力大学学报, 2015, 42(6): 35–42.
MA Shiqiang, YU Lixia, ZHENG Lianqing. Characteristics analysis of MMC-HVDC AC asymmetric fault and protection strategy[J]. Journal of North China Electric Power University, 2015, 42(6): 35–42. (in Chinese) |
| [11] | Olowookere O, Skarvelis-kazakos S, Habtay Y, et al. AC fault ride through of modular multilevel converter VSC-HVDC transmission systems[C]//Proceedings of the universities power engineering conference.[S.l.], IEEE, 2015:1-6. |
| [12] | Zhou Y, Jiang D, Guo J, et al. Analysis and control of modular multilevel converters under unbalanced conditions[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 1986–1995. DOI:10.1109/TPWRD.2013.2268981 |
| [13] |
孔明, 汤广福, 贺之渊, 等.
不对称交流电网下MMC-HVDC输电系统的控制策略[J]. 中国电机工程学报, 2013, 33(28): 41–49.
KONG Ming, TANG Guangfu, HE Zhiyuan, et al. A control strategy for modular multilevel converter based HVDC of unbalanced AC systems[J]. Proceedings of the CSEE, 2013, 33(28): 41–49. (in Chinese) |
| [14] |
王宾, 陆元园.
利用多时刻信息的T接线路单相接地故障单端测距方法[J]. 中国电机工程学报, 2016, 36(10): 2611–2618.
WANG Bin, LU Yuanyuan. Single terminal fault location to single-line-to-ground fault in T transmission line based on sequenced time session data[J]. Proceedings of the CSEE, 2016, 36(10): 2611–2618. (in Chinese) |
| [15] |
葛耀中. 新型继电保护和故障测距的原理与技术[M]. 西安: 西安交通大学出版社, 2007.
GE Yaozhong. Principle and technology of new type of relay protection and fault location[M]. Xi'an: Xi'an jiaotong University Press, 2007. (in Chinese) |
| [16] | Jovcic D, Lamont L, Abbott K. Control system design for VSC transmission[J]. Electric Power Systems Research, 2007, 77(7): 721–729. DOI:10.1016/j.epsr.2006.06.011 |
| [17] | Du C Q, Agneholm E, Olsson G. Use of VSC-HVDC for industrial systems having onsite generation with frequency control[J]. IEEE Transactions on Power Delivery, 2008, 23(4): 2233–2240. DOI:10.1109/TPWRD.2008.2002650 |
| [18] | Leon A E, Mauricio J M, Solsona J A, et al. Adaptive control strategy for VSC-Based systems under unbalanced network conditions[J]. IEEE Transactions on Samrt Grid, 2010, 1(3): 311–319. DOI:10.1109/TSG.2010.2076840 |
| [19] | Du C Q, Bollen M H J, Agneholm E, et al. A new control strategy of a VSC-HVDC system for high-quality supply of industrial plants[J]. IEEE Transactions on Power Delivery, 2007, 22(4): 2386–2394. DOI:10.1109/TPWRD.2007.899622 |
| [20] |
孔祥平, 张哲, 尹项根, 等.
含逆变型分布式电源的电网故障电流特性与故障分析方法研究[J]. 中国电机工程学报, 2013, 33(34): 65–74.
KONG Xiangping, ZHANG Zhe, YIN Xianggen, et al. Study on fault current characteristics and fault analysis method of power grid with inverter interfaced distributed generation[J]. Proceedings of the CSEE, 2013, 33(34): 65–74. (in Chinese) |
| [21] |
罗永捷, 李耀华, 李子欣, 等.
全桥型MMC-HVDC直流短路故障穿越控制保护策略[J]. 中国电机工程学报, 2016, 36(7): 1933–1943.
LUO Yongjie, LI Yaohua, LI Zixin, et al. DC short-circuit fault ride-through control strategy of full-bridge MMC-HVDC systems[J]. Proceedings of the CSEE, 2016, 36(7): 1933–1943. (in Chinese) |
| [22] |
黄磊, 罗伟, 杨冠军.
舟山多端柔性直流系统交流故障穿越能力分析[J]. 电气开关, 2016, 54(3): 22–26.
HUANG Lei, LUO Wei, YANG Guanjun. AC faults ride-through capability analysis of zhoushan MMC-MTDC system[J]. Electrical Switch, 2016, 54(3): 22–26. (in Chinese) |
 2017, Vol. 40
2017, Vol. 40

