焦炉冷鼓系统虽然是整个集气管压力控制系统中的一部分,其控制的初冷器前吸力却对集气管压力的稳定起着至关重要的作用[1-3]。由于冷鼓系统具有时变、非线性,并存在较强干扰,传统的PID控制器在这种条件下,并不能达到要求的性能指标。因此,研究先进的控制算法实现初冷器前吸力控制,具有重要意义。文献[4-5]提出了将模糊理论与PID相结合,把鼓风机作为执行器的控制策略,在一定程度上提高了系统的稳定性。文献[6-7]提出了冷鼓系统的预测控制,提高了系统对复杂工况的适应性。由于焦炉冷鼓系统的复杂性,上述控制虽然能起到一定的调节作用,但处理各种复杂工况和一些未知的干扰仍然不能很好的解决。
随着统计学习理论的完善,SVR为模型辨识注入了新的生命。对比神经网络,SVR在过学习、易陷入最小值,过分依赖经验值等问题上都有较大改善。特别是在非线性系统的辨识上,SVR具有较强的泛化能力,极大的提高了训练能力[8-10]。在将焦化生产分成3种不同工况的前提下,将SVR与预测控制相结合,充分发挥了预测控制能有效克服过程不确定性、非线性和关联性等优点,且SVR可离线辨识冷鼓系统的模型,并利用ASPO算法优化SVR的参数,达到提高模型精度的目的。仿真结果表明,该控制策略具有较强的抗干扰性和稳定性。
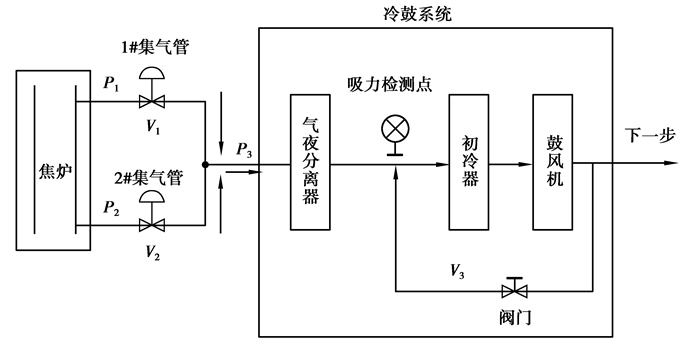
1 焦炉冷鼓系统过程描述与建模 1.1 焦炉冷鼓系统过程描述焦炉冷鼓系统主要由初冷器、鼓风机等装置组成,主要功能是调节初冷器前吸力。图 1给出了焦炉荒煤气传输系统结构示意图,图中标注的部分即是冷鼓系统。
|
图 1 焦炉冷荒煤气传输系统结构示意图 Figure 1 The stuchture of coalgas transmission system |
在焦炉冷鼓系统生产过程中,根据工艺要求,初冷器前吸力要求稳定在-1.0 KPa至-1.4 KPa之间,通过大循环管的阀门可以调节初冷器入口处的吸力P3。根据产生煤气量的大小,将系统分为3种不同的工况:工况1为检修保温工况;工况2为正常生产工况;工况3为推焦加煤工况,不同的工况设定不同的吸力取值。笔者通过控制大循环阀门来调节初冷器前吸力,即控制对象的输入为大循环阀门开度u(k),输出为初冷器前吸力y(k)。
1.2 支持向量回归机进行模型预测考虑到焦炉冷鼓系统具有较强的非线性,传统的模型辨识方法往往不能得到满意的辨识结果,提出基于支持向量回归机的建模方法。
对于一个单输入单输出非线性系统,假设其模型为
| $ \begin{array}{l} y\left( {k + 1} \right) = f\left[{y\left( k \right), y\left( {k-1} \right), \ldots y\left( {k-n} \right), u\left( k \right), u\left( {k-1} \right), \ldots u\left( {k - m} \right)} \right], \\ y \in {R^n}, u \in {R^m}, m \le n, \end{array} $ | (1) |
式中:u和y分别代表对象的输入和输出;m和n分别代表输入、输出多项式的阶次。
引入回归矢量
| $ \mathit{\boldsymbol{\varphi }}\left( k \right) = \left[{y\left( k \right), y\left( {k-1} \right), \ldots y\left( {k-n} \right), u\left( k \right), u\left( {k-1} \right), \ldots u\left( {k - m} \right)} \right], $ | (2) |
则式(1) 可改写为
| $ {y_m}\left( {k + 1} \right) = {f_{{\rm{SVM}}}}\left( {\mathit{\boldsymbol{\varphi }}\left( k \right), \theta } \right), $ | (3) |
式中:θ为系统待辨识的参数。
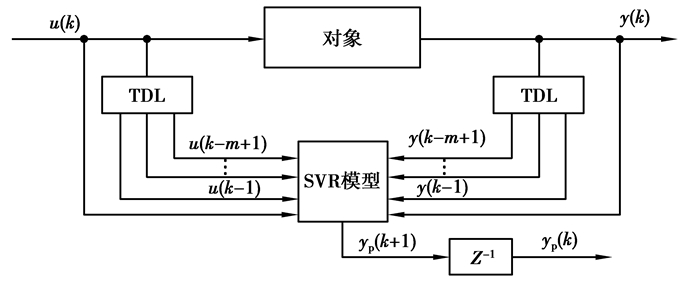
因此,非线性系统辨识的目的即:确定式(3) 中fSVM(·)的具体形式和参数矢量θ的具体值。对于并联结构的SVR辨识模型,由于学习的开始并不能保证ym逼近y,偏差在递推过程中会产生积累效应,故采取了串-并模型的辨识结构,如图 2所示。
|
图 2 串-并模型的SVR辨识结构图 Figure 2 SVR identification structure of serial-parallel model |
通过核函数将输入空间经过非线性变换φ映射到高维线性可分空间,得SVR辨识的参数和结果为
| $ \theta = \sum\limits_{i = 1}^N {(a_i^*-{a_i})\varphi ({x_i})}, $ | (4) |
| $ f(x) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}(x) + b = \sum\limits_{i = 1}^N {(a_i^*-{a_i})K\left( {u\left( i \right), u\left( k \right)} \right) + b} {\rm{, }} $ | (5) |
式中:a*为Langrange乘子;N为训练样本的个数。
非线性核函数一般采用RBF核函数
| $ K\left( {u\left( i \right), u\left( k \right)} \right) = {\rm{exp}}\left\{ {\frac{{-{{\left| {u\left( k \right)-u\left( i \right)} \right|}^2}}}{{2{\delta ^2}}}} \right\}, $ | (6) |
则模型估计输出为
| $ {y_m}\left( {k + 1} \right) = \sum\limits_{i = 1}^N {\beta K\left( {u\left( i \right), u\left( k \right)} \right) + b}。$ | (7) |
采用自适应权值粒子群优化算法对SVR的不敏感系数ε,惩罚参数C及径向基核函数的宽度系数γ进行优化。
APSO算法介绍如下:
假设在一个S维的目标搜索空间中,有m个粒子组成一个群体,每个粒子的位置都是一个潜在解。记第i个粒子的位置为Xis,第i个粒子迄今为止搜索到的最优位置为Pis,整个粒子群迄今为止搜索到的最优位置为Pgs.
设f(x)为最小化的目标函数,则粒子i的当前最好位置由下式给出
| $ {p_i}\left( {t + 1} \right) = \left\{ \begin{array}{l} {p_i}\left( t \right) \to f[{x_i}\left( {t + 1} \right)\left] { \ge f} \right[{p_i}\left( t \right)], \\ {X_i}\left( {t + 1} \right) \to f[{x_i}\left( {t + 1} \right)\left] { \le f} \right[{p_i}\left( t \right)]。\end{array} \right. $ | (8) |
对粒子的速度和位置作以下操作
| $ \begin{array}{l} {v_{is}}\left( {t + 1} \right) = {\rm{ }}w \cdot {v_{is}}\left( t \right) + {c_1}{r_{1s}}\left( {{p_{is}}\left( t \right)-{x_{is}}\left( t \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}{c_2}{r_{2s}}\left( {{p_{gs}}\left( t \right)-{x_{is}}\left( t \right)} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}{x_{is}}\left( {t + 1} \right) = {x_{is}}\left( t \right) + {v_{is}}\left( {t + 1} \right), \end{array} $ | (9) |
式中:i=[1, m],s=[1, S];c1为局部学习因子,c2为全局学习因子,c2一般比c1大些;r1和r2为相互独立的伪随机数,服从[0, 1]上的均匀分布;w为非负数,称为动力常量,通过调整w的大小跳出局部最小值。
为了平衡PSO的全局搜索能力和局部改良能力,采用非线性的动态权重系数公式,表达式如下
| $ w = \left\{ \begin{array}{l} {w_{{\rm{min}}}} + {\rm{ }}\frac{{({w_{{\rm{max}}}}-{w_{{\rm{min}}}}) * (f-{f_{{\rm{min}}}})}}{{{f_{{\rm{avg}}}}-{f_{{\rm{min}}}}}}, f \le {f_{{\rm{avg}}}};\\ {w_{{\rm{max}}}}f > {f_{{\rm{avg}}}}, \end{array} \right. $ | (10) |
wmax和wmin分别为w的最大值和最小值,f表示粒子当前的目标函数值,favg和fmin分别表示当前所有粒子的平均目标值和最小目标值。
APSO算法步骤:
将APSO算法运用到SVR模型参数辨识中,算法步骤如下
Step1:数据集处理。确定SVR的训练集和测试集。
Step2:初始化种群和速度。
Step3:计算粒子适应度值。适应度值定义为
| $ f = {\rm{ }}\frac{1}{m}\sum\limits_{i = 1}^m {({y_r}-{y_m})} 。$ | (11) |
根据此式找到个体极值和群体极值。当多组优化向量(C, ε, γ)对应同一适应度值时,选取C较小的粒子,C过高会导致过学习状态。
Step4:根据式(9) 更新粒子的速度和位置,产生新种群,并对粒子的速度和位置进行越界检查。
Step5:根据式(8) 更新个体极值Pis和群体极值Pgs。
Step6:检查结束条件,若满足,则结束寻优,确定最优粒子及SVR的最优参数。否则返回Step3。
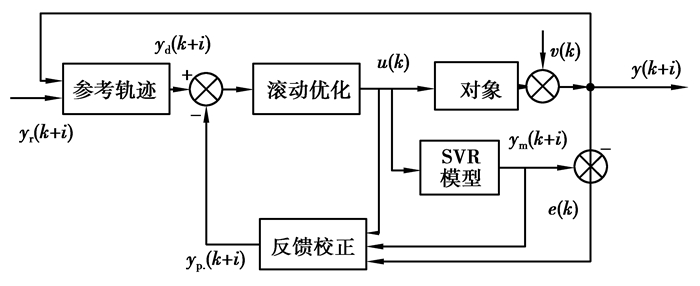
2 基于SVR的焦炉冷鼓系统预测控制基于SVR模型的焦炉冷鼓系统预测控制系统框图如图 3所示
|
图 3 基于SVR的预测控制系统框图 Figure 3 The diagram of predictive control based on SVR |
图中,yr为期望输出,ym为预测模型的输出,yp为经反馈校正后的预测输出,u为控制量。
SVR模型为具有被控系统特性的动态模型,基于此模型对系统行为进行优化。通过滚动优化,按照给定的有限时域目标函数优化过程性能,找出最优控制序列你,并将该序列的第一元素施加给被控对象。
由图可知系统输出误差
| $ e\left( k \right) = {y_m}\left( k \right)-y\left( k \right)。$ | (12) |
优化目标函数
| $ \begin{array}{l} {\rm{min}}J\left( k \right) = \sum\limits_{j = 1}^P {\left[{{\alpha _j}{{[{y_p}\left( {k + j} \right)-{y_r}\left( {k + j} \right)]}^2} + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\beta _j}\sum\limits_{j = 1}^N {{{[{r_j}\Delta u\left( {k + j-1} \right)]}^2}} } \right], \end{array} $ | (13) |
式中:P为优化时域,N为控制时域,rj为控制加权系数,一般取为常数。在目标函数中加入控制量约束项
由于实际存在模型失配、环境干扰等未知因素,式(7) 给出的预测值可能偏离实际值,利用式(12) 所得误差e(k)建立反馈校正
| ${y_{\rm{p}}}\left( {k + 1} \right) = {y_{\rm{m}}}\left( {k + 1} \right) + he\left( k \right), $ | (14) |
h为误差修正系数,根据实际应用的效果进行调整。
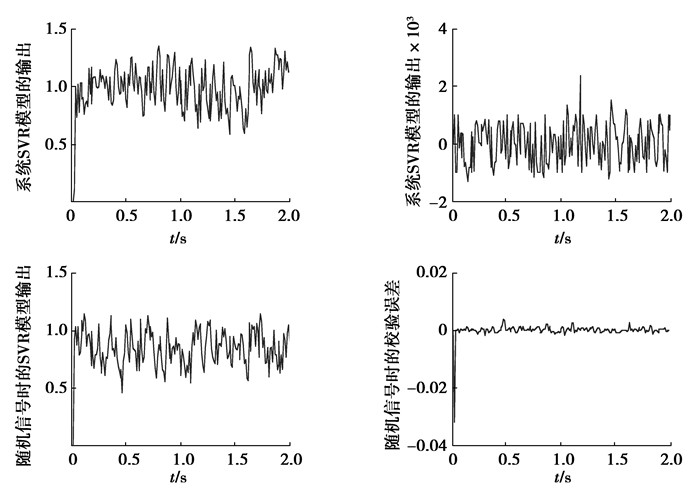
3 实验仿真结果与分析取输入输出数据训练SVR模型,合理选用辨识输入信号是保证获得理想辨识结果的关键之一。由于系统辨识中所用到的数据通常都含有噪声,白噪声作为简单的随机过程,可以模拟现场所采集的数据,将白噪声过程离散化得到白噪声序列作为输入加到利用SVR所辨识的系统中,图 4为基于SVR模型的输出及校验结果。仿真结果显示校验误差达到了10-2数量级,表明用SVR建立的该系统推广性较好。
|
图 4 基于SVR的系统建模及模型校验 Figure 4 System modeling and model checking based on SVR |
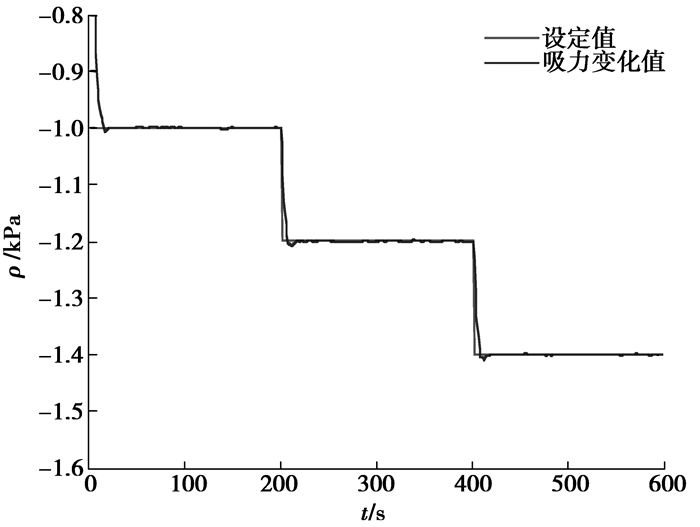
在获得预测模型之后,利用预测控制器预测未来输出。预测控制器的预测参数为:最小输出长度N1=2,预测长度P=8,控制长度N=2;模拟焦炉冷鼓系统的3个工况:0~200 s为工况1,设定值为-1.0 kPa;200~400 s为工况2,设定值为-1.2 kPa;400~600 s为工况3,设定值为-1.4 kPa。预测控制结果如图 5所示
|
图 5 预测控制结果 Figure 5 The result of predictive control |
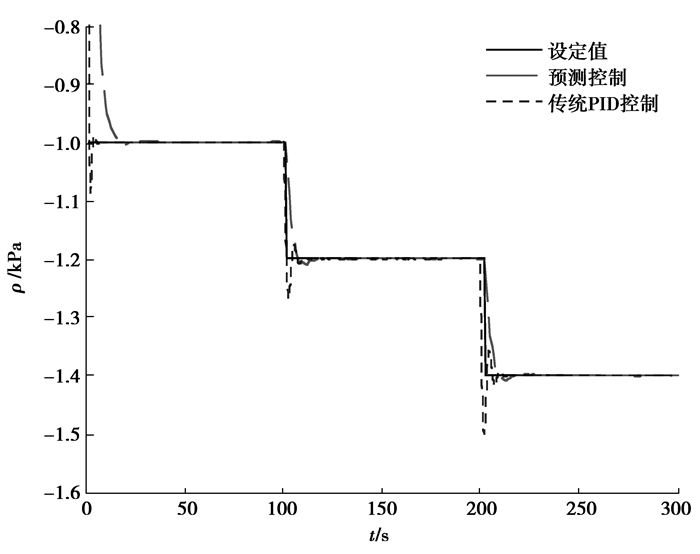
为了验证预测控制的性能,将其与传统的PID控制相对比。由图 6可见,较传统的PID控制,预测控制有更小的超调量,能更加平稳快速的跟踪设定值。
|
图 6 预测控制、PID控制对比图 Figure 6 Predictive control compared with PID control |
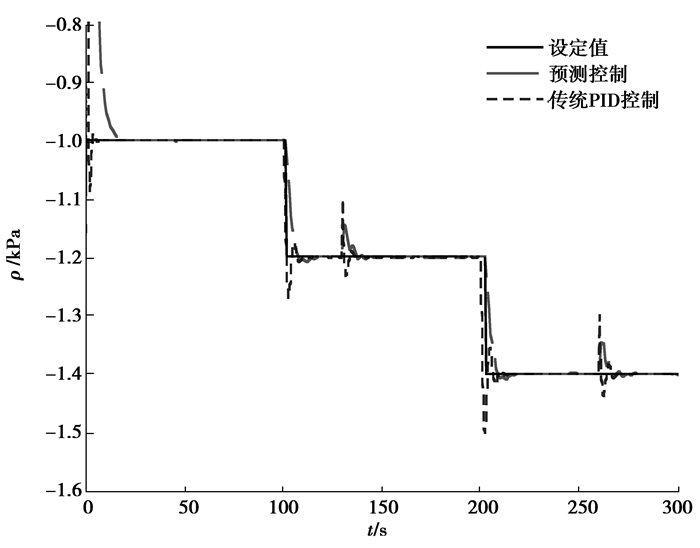
为了进一步验证预测控制的性能,模拟现场的工况环境。分别在t=130 s和t=260 s时加上d=0.028的干扰,仿真结果如图 7所示
|
图 7 干扰条件下预测控制、PID控制对比图 Figure 7 Prdictive contril compared with PID control under distwbance |
仿真结果表明,预测控制具有更好的抗干扰性,提高了系统的鲁棒性。
4 结论设计的基于SVR的预测控制方法应用于焦炉冷鼓系统,针对焦炉不同工况条件和冷鼓系统被控对象复杂的情况,用SVR辨识建模,用APSO算法优化SVR参数,以提高冷鼓系统的输出跟踪精度。仿真结果表明:系统经过SVR离线辨识后进行预测控制,通过实时调节大循环阀门开度,可实现快速稳定初冷器前吸力的目的;在出现工况改变的情况下,预测控制器能及时地作出调节,保证初冷器前吸力稳定在要求的范围内。该智能控方案满足初冷器前吸力控制的实际输出值与输入值之间的静态指标要求,且具有良好的动态性能。
| [1] |
高忠仁.
焦炉集气管压力与鼓风机综合控制系统[J]. 冶金自动化, 2009, 33(06): 7–12.
GAO Zhongren. The integrated control system of coke oven gas collector pressure and air blower[J]. Metallurgical Automation, 2009, 33(06): 7–12. (in Chinese) |
| [2] |
杨耀峰. 基于DCS的焦化冷鼓控制系统设计[D]. 太原: 太原科技大学, 2013. YANG Yaofeng. Design of the control system of the coke oven blowing cooler system based on DCS[D]. Taiyuan:Taiyuan University of Science and Technology, 2013.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10109-1013183523.htm |
| [3] |
周国雄, 赖旭芝, 曹卫华, 等.
焦炉集气管压力智能解耦控制系统的应用[J]. 中南大学学报(自然科学版), 2006, 37(03): 558–561.
ZHOU Guoxiong, LAI Xuzhi, CAO Weihua, et al. Application of intelligent decoupling control system for coke oven collector pressure[J]. Journal of Central South University(Natural Science Edition), 2006, 37(03): 558–561. DOI:10.3969/j.issn.1672-7207.2006.03.027 (in Chinese) |
| [4] |
肖志刚.
基于模糊理论的焦炉集气管压力控制系统的设计与实现[J]. 科学技术与工程, 2007.
XIAO Zhigang. Design and implementation of the control system of coke oven gas collector pressure based on fuzzy theory[J]. Science Technology and Engineering, 2007. DOI:10.3969/j.issn.1671-1815.2007.01.036 (in Chinese) |
| [5] |
高宪文, 赵亚平.
焦炉模糊免疫自适应PID控制的应用研究[J]. 控制与策, 2005, 20(12): 1346–1349.
GAO Xianwen, ZHAO Yaping. Application of fuzzy immune adaptive PID control for coke oven[J]. Control andDecision Making, 2005, 20(12): 1346–1349. (in Chinese) |
| [6] | Li H. Model reference control based oncompensatory fuzzy neural network for gas collectors of coke oven[C]//Intelligent Control and Automation Science.[S.L.]:IEEE, 2013:654-659. |
| [7] |
张世峰, 金科, 冯强.
焦炉鼓冷系统建模与Gpc控制器设计[J]. 燃料与化工, 2014, 3(1): 57–60.
ZHANG Shifeng, JIN Ke, FENG Qiang. Coke oven blowing cooler system modeling and controller design of gpc[J]. Fuel and Chemical Engineering, 2014, 3(1): 57–60. (in Chinese) |
| [8] | Shi W, Wang J, Shi Y, et al. Clustering LS-SVM models for the prediction of unburned carbon content in fly ash[C]//Control and Decision Conference.[S.L.]:IEEE, 2015:1919-1924. |
| [9] | Lei B, Wang W, Li Z. On-line predictive control based on LS-SVM[C]//Intelligent Control and Automation, 2008.[S.L.]:IEEE, 2008:7870-7873. |
| [10] | Ren Y, Bai G. Determination of optimal SVM parameters by using GA/PSO[J]. Journal of Computers, 2010, 5(8): 1160–1168. |
| [11] | Nisha M G, Pillai G N. Nonlinear model predictive control with relevance vector regression and particle swarm opti-mization[J]. Journal of Control Theory & Applications, 2013, 11(4): 563–569. |
| [12] |
吴东升, 王大志, 杨青, 等.
基于ACPSO优化SVR的棒材连轧轧制力预测研究[J]. 仪器仪表学报, 2012, 33(11): 2579–2585.
WU Dongsheng, WANG Dazhi, YANG Qing, et al. SVR bar continuous rolling force prediction based on ACPSO optimization[J]. Chinese Journal of Scientific Instrument, 2012, 33(11): 2579–2585. DOI:10.3969/j.issn.0254-3087.2012.11.026 (in Chinese) |
| [13] |
邵信光, 杨慧中, 陈刚.
基于粒子群优化算法的支持向量机参数选择及其应用[J]. 控制理论与应用, 2006, 23(5): 740–743.
SHAO Xinguang, YANG Huizhong, CHEN Gang. Parameter selection of support vector machine based on particle swarm optimization algorithm and its application[J]. Control Theory and Application, 2006, 23(5): 740–743. (in Chinese) |
| [14] | Cai C, Li J, Xia Q. LS-SVM based nonlinear adaptive direct generalized predictive control[C]//International Conference on Automatic Control and Artificial Intelligence.[S.L.]:IEEE, 2012:1324-1326. |
| [15] | Wang X, Du Z, Shen Y X. Hybrid SVR-PSO for identification of nonlinear system[J]. International Journal of Applied Mathematics & Statistics, 2013, 49(19): 229–237. |
 2017, Vol. 40
2017, Vol. 40



