2. 重庆大学 计算机学院, 重庆 400044
2. College of Computer Science, Chongqing University, Chongqing 400044, P.R.China
交通拥堵已成为制约社会经济发展的重要因素之一, 备受学界关注[1]。为了探索交通拥堵内在运行机制, 一系列交通流模型被相继提出[2-8]。其中Bando等[9]于1995年提出的优化速度(OB, optimal velocity)交通流模型最为经典, 该模型可以刻画拥堵严重时车辆走走停停等实际交通现象。1999年, Konishi等[10]将OV模型离散化, 得到耦合映射(CM, coupled map)跟驰模型, 该模型能够描述单车道上无倒车现象的车流演化机制, 但其只适应在开放边界条件下验证。随后, 学者们设计延时反馈控制方法并引入到CM模型中, 验证对拥堵的抑制性能, 仿真结果显示拥堵影响范围明显减小。Zhao等[11]利用前后车相对速度信息设计了更为简洁的反馈控制器, 其拥堵抑制效果较文献[10]提出的CM模型更优。韩祥临等[12]将前后多车诱导信息引入拥堵控制器, 以期实时准确地把握路况信息, 提前控制车速, 使车流运行稳定, 从而有效抑制拥堵。此后, 国内外学者取得了一系列与拥堵抑制方法相关的研究成果[13-15]。
上述拥堵抑制方法均能很好地控制车流运动状态, 车流能够保持稳定状态运行, 进而减小了拥堵的影响范围, 但未考虑驾驶员驾车时对车速波动的要求。在实际驾车过程中, 驾驶员在考虑自身舒适性时, 总期望车速波动不大, 即稳态期望速度效应。因此, 研究在文献[12]的拥堵抑制方法的基础上, 考虑稳态期望速度效应对交通拥堵的影响, 提出一个新的拥堵抑制方法, 结合CM模型, 形成新的拥堵控制跟驰模型。利用现代控制理论, 得到交通系统稳定运行的临界条件。同时, 在开放的边界条件下, 对新模型进行数值仿真, 验证其对拥堵的抑制性能。
1 拥堵控制跟驰模型CM拥堵抑制跟驰模型[10]的车流运动方程为
| $ \begin{array}{l} {v_i}\left( {n + 1} \right) = {\alpha _i}\left[ {V_i^{{\rm{OP}}}\left( {{y_i}\left( n \right)} \right) - {v_i}\left( n \right)} \right]T + {v_i}\left( n \right) + {u_i}\left( n \right),\\ {y_i}\left( {n + 1} \right) = {v_{i + 1}}T - {v_i}\left( n \right)T + {y_i}\left( n \right), \end{array} $ | (1) |
式中:vi(n)和yi(n)分别为第i辆车在t= nT的速度和车头距; T为采样时间; αi和ViOP(·)分别为第i辆车驾驶员对外界交通状况的敏感程度和控制车速达到的最优速度; ui(n)为离散反馈控制信号, 具体为
| $ \begin{array}{l} {u_i}\left( n \right) = k_i^c{w_i}\left( n \right) + k_i^d\left[ {{v_i}\left( n \right) - {v_i}\left( {n - 1} \right)} \right],\\ {w_i}\left( {n + 1} \right) = k_i^a{w_i}\left( n \right) + k_i^b\left[ {{v_i}\left( n \right) - {v_i}\left( {n - 1} \right)} \right], \end{array} $ | (2) |
式中:kia, kib, kic, kid∈R均为控制参数; ui(n)的形式复杂, 其4个控制参数设计复杂, 计算量大, 进而使得控制策略的制定较困难。
针对CM拥堵抑制模型缺点, Zhao等[11]设计一个包含前后车速度差信息的拥堵抑制跟驰模型, 其运动学方程为
| $ \begin{array}{l} {v_i}\left( {n + 1} \right) = {\alpha _i}\left[ {V_i^{{\rm{OP}}}\left( {{y_i}\left( n \right)} \right) - {v_i}\left( n \right)} \right]T + {v_i}\left( n \right) + k\Delta {u_i}\left( n \right),\\ {y_i}\left( {n + 1} \right) = {v_{i + 1}}T - {v_i}\left( n \right)T + {y_i}\left( n \right), \end{array} $ | (3) |
式中:k是反馈控制增益; Δvi(n)=vi+1(n)-vi(n)为第i+1辆车与第i辆车的速度差; kΔvi(n)为拥堵抑制项, 该项形式更简单, 其抑制拥堵能力较CM模型更强。
在实际交通中, 驾驶员可以借助智能交通系统(ITS, intelligent transportation system)获取当前车周边交通路况信息。于是, 韩祥临等[12]将周边车流信息引入到CM模型, 提出一个基于ITS信息的拥堵抑制模型(ITS-CM), 具体为
| $ \begin{array}{l} {v_i}\left( {n + 1} \right) = {\alpha _i}\left[ {V_i^{{\rm{OP}}}\left( {{y_i}\left( n \right)} \right) - {v_i}\left( n \right)} \right]T + {v_i}\left( n \right) + \sum\limits_{l = 1}^s {{k_l}\left[ {{v_{i + l}}\left( n \right) - {v_{i + l - 1}}\left( n \right)} \right]} ,\\ {y_i}\left( {n + 1} \right) = {v_{i + 1}}T - {v_i}\left( n \right)T + {y_i}\left( n \right), \end{array} $ | (4) |
式中, s为当前车的前导车数量, s≥2, i=1, 2, …, N。仿真结果表明, 诱导信息能够降低拥堵影响的范围。
上述模型均能很好地抑制拥堵, 然而, 这些模型不适合研究稳态期望速度效应对拥堵演化机制的影响。实际上, 从驾驶舒适性和车辆燃料使用效率角度考虑, 驾驶员一般期望车辆以平稳状态行驶, 避免急加速和急减速。同时, 在ITS环境下, 驾驶员可以获得前后多辆车的运动状态信息[12]。因此, 文中考虑前后车速度与稳态速度差值对拥堵形成机制的影响, 设计一个考虑多车稳态期望速度综合效应(MVSSDSE, multi-vehicles’ steady-state desired speed effect)的拥堵抑制方法, 代入CM模型, 形成一个新的拥堵控制模型, 简称MVSSDSE-CM模型, 其运动学方程
| $ \begin{array}{*{20}{c}} {{v_i}\left( {n + 1} \right) = {\alpha _i}\left[ {V_i^{{\rm{OP}}}\left( {{y_i}\left( n \right)} \right) - {v_i}\left( n \right)} \right]T + {v_i}\left( n \right) +\\ \sum\limits_{l = 1}^s {{k_l}\left[ {{v_{i + l}}\left( n \right) - {v_0}} \right]} - mH\left( {\eta - {y_i}\left( n \right)} \right)\left( {{v_{i - 1}}\left( n \right) - {v_0}} \right),}\\ {{y_i}\left( {n + 1} \right) = {v_i}T - {v_i}\left( n \right)T + {y_i}\left( n \right),} \end{array} $ | (5) |
式(5)中拥堵控制信号项为
| $ {u_i}\left( n \right) = \sum\limits_{l = 1}^s {{k_l}\left[ {{v_{i + l}}\left( n \right) - {v_0}} \right]} - mH\left( {\eta - {y_i}\left( n \right)} \right)\left( {{v_{i - 1}}\left( n \right) - {v_0}} \right), $ | (6) |
式中:vi-1(n)为第i车紧邻后车的速度; v0为车流的稳态车速; η为车流保持稳定有序运行的安全间距; yi(n)第i车的车头间距, m是交通控制系统的反馈增益。H(·)为Heaviside函数, 具体为:
| $ H\left( {\eta - {y_i}\left( n \right)} \right) = \left\{ \begin{array}{l} 0\;\;\;\;\;\eta - {y_i}\left( n \right) > 0,\\ 1\;\;\;\;\;\eta - {y_i}\left( n \right) < 0。\end{array} \right. $ | (7) |
当η-yi(n)<0, 系统的拥堵抑制方法可以简化为
| $ {u_i}\left( n \right) = \sum\limits_{l = 1}^s {{k_l}\left[ {{v_{i + l}}\left( n \right) - {v_0}} \right]} ; $ | (8) |
当η-yi(n)≥0, 系统的拥堵抑制方法可以简化为
| $ {u_i}\left( n \right) = \sum\limits_{l = 1}^s {{k_l}\left[ {{v_{i + l}}\left( n \right) - {v_0}} \right]} - m\left( {{v_{i - 1}}\left( n \right) - {v_0}} \right)。$ | (9) |
文中只考虑前后车的稳态速度差效应对车流运动特性的影响, 则MVSSDSE-CM简化为
| $ \begin{array}{l} {v_i}\left( {n + 1} \right) = {\alpha _i}\left[ {V^{{\rm{OP}}}\left( {{y_i}\left( n \right)} \right) - {v_i}\left( n \right)} \right]T + {v_i}\left( n \right) + k\left( {{v_{i + 1}}\left( n \right) - {v_i}\left( n \right)} \right) + \\ \sum\limits_{l = 1}^s {{k_l}\left[ {{v_{i + l}}\left( n \right) - {v_0}} \right]} - m\left( {{v_{i - 1}}\left( n \right) - {v_0}} \right),\\ {y_i}\left( {n + 1} \right) = {v_{i - 1}}\left( n \right)T - {v_i}\left( n \right)T + {y_i}\left( n \right), \end{array} $ | (10) |
当车流处于不稳定状态时,
采用文献[10]中车辆运行的稳定状态, 具体为
| $ {\left[ {{v_i}^ * ,{y_i}^ * } \right]^{\rm{T}}} = {\left[ {{v_0},\frac{{{v_0}}}{{{r_i}}} - \frac{{{\zeta _i}}}{2} + {\eta _i}} \right]^{\rm{T}}}。$ | (11) |
运用线性控制理论, 将式(10)在稳态值附近进行线性化, 其描述如下
| $ \begin{array}{*{20}{c}} {\delta {v_i}\left( {n + 1} \right) = {\alpha _i}\left[ {{r_i}\delta {y_i}\left( n \right) - \delta {v_i}\left( n \right)} \right]T + \delta {v_i}\left( n \right) + k\left( {\delta {v_{i + 1}}\left( n \right) - \delta {v_i}\left( n \right)} \right) \\ + \sum\limits_{l = 1}^s {{k_l}\delta {v_{i + 1}}\left( n \right) - m\delta {v_{i - 1}}\left( n \right)} ,}\\ {\delta {y_i}\left( {n + 1} \right) = \delta {v_{i + 1}}T - \delta {v_i}\left( n \right)T + \delta {y_i}\left( n \right),} \end{array} $ | (12) |
式中, δyi(n)=yi(n)-yi*, δvi(n)=vi(n)-vi*, δvi(n)=vi(n)-vi*。将式(12)写成状态空间表达式:
| $ \left( {\begin{array}{*{20}{c}} {\delta {v_i}\left( {n + 1} \right)}\\ {\delta {y_i}\left( {n + 1} \right)} \end{array}} \right) =\\ \left( {\begin{array}{*{20}{c}} {1 - {\alpha _i}T - k}&{{\alpha _i}{r_i}T}\\ { - T}&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\delta {v_i}\left( n \right)}\\ {\delta {y_i}\left( n \right)} \end{array}} \right) +\\ \left( {\begin{array}{*{20}{c}} { - m}&{k + {k_1}}&{{k_2}}& \cdots &{{k_s}}\\ 0&T&0&{\bf{0}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\delta {v_{i - 1}}\left( n \right)}\\ {\delta {v_{i + 1}}\left( n \right)}\\ {\delta {v_{i + 2}}\left( n \right)}\\ \vdots \\ {\delta {v_{i + s}}\left( n \right)} \end{array}} \right), $ | (13) |
| $ \mathit{\boldsymbol{\delta }}{\mathit{\boldsymbol{v}}_i}\left( n \right) = \left( {\begin{array}{*{20}{c}} 1&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\delta {v_i}\left( n \right)}\\ {\delta {y_i}\left( n \right)} \end{array}} \right)。$ |
车辆系统的传递函数Gi(z)为
| $ \begin{array}{*{20}{c}} {{G_i}\left( z \right) = \left( {\begin{array}{*{20}{c}} 1&0 \end{array}} \right){{\left( {\begin{array}{*{20}{c}} {z - 1 + {\alpha _i}T + k}&{ - {\alpha _i}{r_i}T}\\ T&{z - 1} \end{array}} \right)}^{ - 1}}\left( {\begin{array}{*{20}{c}} { - m}&{k + {k_1}}&{{k_2}}& \cdots &{{k_s}}\\ 0&T&0&{\bf{0}}&0 \end{array}} \right) = }\\ {\left( {\begin{array}{*{20}{c}} 1&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {z - 1}&{{\alpha _i}{r_i}T}\\ { - T}&{z + k + {r_i}T - 1} \end{array}} \right)\left( {\begin{array}{*{20}{c}} { - m}&{k + {k_1}}&{{k_2}}& \cdots &{{k_s}}\\ 0&T&0&{\bf{0}}&0 \end{array}} \right) = }\\ {\left[ { - m\left( {z - 1} \right),{k_1}\left( {z - 1} \right) + {\alpha _i}{r_i}{T^2},{k_2}\left( {z - 1} \right), \cdots ,{k_s}\left( {z - 1} \right)} \right]/{P_i}\left( z \right),} \end{array} $ | (14) |
式中:Pi(z)=z2+aiz+bi, ai=αiT+k-2, bi=1-αiT-k+αiriT2。
另外这里的kl参数是减函数, 即kl+1/kl<1, 因为考虑到实际车流运行过程中, 驾驶员对与其空间距离很远的车辆的运动状态敏感程度不高。这里kl取值为[16]
| $ {k_l} = \frac{2}{{{3^l}}}R\left( {l = 1,2, \cdots ,s - 1} \right), $ | (15) |
式中:s为整个车队中在当前车前面运行的车辆数量; R表示反馈增益因子。下面给出交通系统运行稳定的引理:
引理1 根据控制系统理论, R同时满足条件①和②式, 式(12)处于稳定运行状态:
① Pi(z)是稳定的;
②
根据引理1, 给出了控制系统临界稳定的定理。
定理1 当MVSSDSE-CM模型中反馈增益m满足以下5种条件时, 车流处于稳定状态。
条件Ⅰ 当0<αiriT2<2和αiT>10/3时, m取值范围为
| $ \max \left\{ {1 - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2},{R_{11}}} \right\} < m < \frac{{4 - 2{\alpha _i}T - 2{k_1} + 2k + {\alpha _i}{r_i}{T^2}}}{2}, $ | (16) |
式中
| $ \begin{array}{l} {R_{11}} = \frac{{4 - 4{\alpha _i}T + \alpha _i^2{T^2} + {k^2} - \alpha _i^2{r_i}{T^3} + 2{\alpha _i}{r_i}{T^2} - 2k}}{{{\alpha _i}T - 10/3}} + \\ \frac{{\left[ {\left( {4{\alpha _i}{r_i}{T^2} + 12k{\alpha _i}T - 2{k_1} - 6{\alpha _i}{r_i}{T^2}} \right)R/9 - \left( {\frac{2}{9} + \frac{1}{{{3^{s - 1}}}} + \sum\limits_{l = 2}^s {\frac{4}{{{3^{l + 1}}}}} } \right){R^2}} \right]1/2}}{{{\alpha _i}T - 10/3}}。\end{array} $ | (17) |
条件Ⅱ 当0<αiriT2<2和αiT<10/3时, m取值范围为
| $ 1 - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2} < m < \min \left\{ {\frac{{4 - 2{\alpha _i}T + 2{k_1} - 2k + {\alpha _i}{r_i}{T^2}}}{2},{R_{12}}} \right\}。$ | (18) |
条件Ⅲ 当2<αiriT2<4和αiT>2/3时, m取值范围为
| $ \begin{array}{l} \max \left\{ { - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2},{R_{21}}} \right\} < m < \\ \min \left\{ {1 - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2},\frac{{4 - 2{\alpha _i}T + 2{k_1} - 2k + {\alpha _i}{r_i}{T^2}}}{2}} \right\}, \end{array} $ | (19) |
式中
| $ \begin{array}{l} {R_{12}} = \frac{{4 - 4{\alpha _i}T + \alpha _i^2{T^2} + {k^2} - \alpha _i^2{r_i}{T^3} + 2{\alpha _i}{r_i}{T^2} - 2k}}{{{\alpha _i}T - 10/3}} - \\ \frac{{\left[ {\left( {4{\alpha _i}{r_i}{T^2} + 12k{\alpha _i}T - 2{k_1} - 6{\alpha _i}{r_i}{T^2}} \right)R/9 - \left( {\frac{2}{9} + \frac{1}{{{3^{s - 1}}}} + \sum\limits_{l = 2}^s {\frac{4}{{{3^{l + 1}}}}} } \right){R^2}} \right]1/2}}{{{\alpha _i}T - 10/3}}。\end{array} $ | (20) |
条件Ⅳ 当0<αiriT2<2和αiT<2/3时, m取值范围为
| $ \begin{array}{l} - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2} < m < \\ \min \left\{ {1 - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2},\frac{{4 - 2{\alpha _i}T + 2{k_1} - 2k + {\alpha _i}{r_i}{T^2}}}{2},{R_{21}}} \right\}, \end{array} $ | (21) |
式中
| $ \begin{array}{l} {R_{21}} = \frac{{4 - 4{\alpha _i}T + \alpha _i^2{T^2} + {k^2} - \alpha _i^2{r_i}{T^3} + 2{\alpha _i}{r_i}{T^2} - 2k}}{{{\alpha _i}T - 10/3}} + \\ \frac{{\left[ {\left( {2{\alpha _i}{r_i}{T^2} + 8k{\alpha _i}T - 2{k_1} - {\alpha _i}{r_i}{T^2}} \right)R/9 + \left( {\frac{2}{9} + \frac{1}{{{3^{s - 1}}}} + \sum\limits_{l = 2}^s {\frac{4}{{{3^{l + 1}}}}} } \right){R^2}} \right]1/2}}{{{\alpha _i}T - 10/3}}。\end{array} $ |
条件Ⅴ 当0<αiriT2<2和αiT>4/3时, m取值范围为
| $ \max \left\{ { - {\alpha _i}T + {k_1} - \lambda + {\alpha _i}{r_i}{T^2},{R_{31}}} \right\} < m < \frac{{4 - 2{\alpha _i}T + 2{k_1} - 2\lambda + {\alpha _i}{r_i}{T^2}}}{2}, $ | (22) |
式中
| $ \begin{array}{l} {R_{31}} = \frac{{4 - 4{\alpha _i}T + \alpha _i^2{T^2} + {k^2} - \alpha _i^2{r_i}{T^3} + 2{\alpha _i}{r_i}{T^2}}}{{{\alpha _i}T - 10/3}} + \\ \frac{{\left[ {2\left( {{\alpha _i}{r_i}{T^2} + 2k{\alpha _i}T - 2{k_1} - {\alpha _i}{r_i}{T^2}} \right)R/9 + \left( {\frac{2}{9} + \frac{1}{{{3^{s - 1}}}} + \sum\limits_{l = 2}^s {\frac{4}{{{3^{l + 1}}}}} } \right){R^2}} \right]1/2}}{{{\alpha _i}T - 10/3}}。\end{array} $ |
定理1证明过程详见附录A。
依据上述条件, 通过设置反馈增益m来实现对式(10)中拥堵的抑制。该控制方案较文献[10]提出的控制方案更简洁, 只需设置反馈增益m一个参数即可。且m值确定是在一定的范围内, 这使得制定抑制拥堵控制策略变的更加灵活。
3 数值仿真为了验证第2节中理论推导是否正确。在开放的边界条件下, 对MVSSDSE-CM进行数值仿真[10], 设置其中参数初始值为
| $ \eta = 25.0{\rm{m}},\zeta = 23.3{\rm{m}},v_j^{\max } = 33.6{\rm{m}}/{\rm{s,}}{\alpha _j} = 2.0{{\rm{s}}^{ - 1}}, $ |
| $ {v_0} = 20{\rm{m}}/{\rm{s,}}{T_1} = 0.1{\rm{s,}}\Delta {x^{\min }} = 7.02{\rm{m}},{r_j} = v_i^{\max }/\zeta \approx 1.44{{\rm{s}}^{ - 1}}。$ |
假设所有车辆的参数相同, 初始位置和速度设置为[10]
| $ {x_i}\left( 0 \right) = \sum\limits_{j = i + 1}^N {y_j^ * } ,{y_j}\left( 0 \right) = y_j^ * ,{v_i}\left( 0 \right) = v_j^ * ,i = 1,2, \cdots ,N。$ | (23) |
为了验证MVSSDSE-CM对拥堵的抑制性能, 本文首先须将m的取值范围求出。将上述初始设置参数代入定理1中, 通过计算得到初始参数满足条件Ⅰ、条件Ⅵ和条件Ⅴ, 并求出m的取值范围, 即0<m<0.214 5。反馈增益的设计程序可以参见文献[10]。下面通过模拟仿真的方式选择最佳反馈增益m。
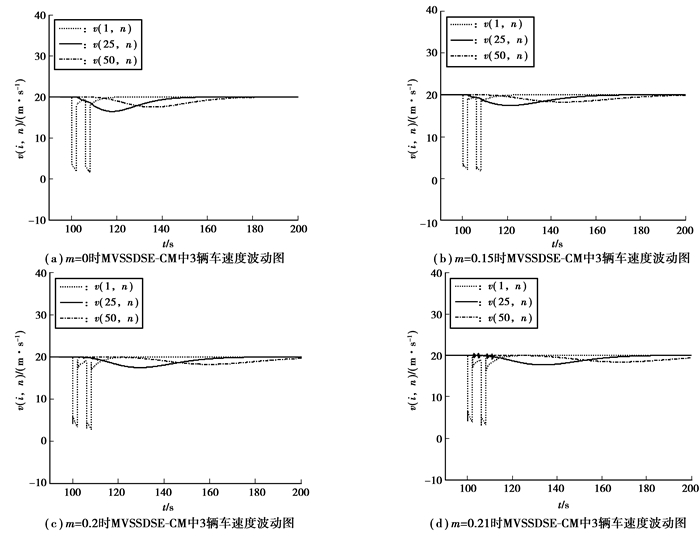
在车流运行模拟过程中, 将车队中头车在100 s和106 s处分别停止3 s来观察车流运行状态。图 1分别显示了不同m值(即m=0, 0.15, 0.20和0.21)下MVSSDSE-CM的第1辆车、第25辆车和第50辆车的速度波动情况(图中t=nT)。当m=0时, MVSSDSE-CM简化成OV模型。由图 1(a)可见, 3辆车的车速波动幅度很大, 第25辆车和第50辆车随着时间的演化, 其车速最终逐渐趋于稳定。图 1(b)与图 1(c)较图 1(a), 车速波动幅度更小, 车流平稳性能更好, 而图 1(c)中的车流的稳定性能最优; 图 1(d)中, 头车停止后, 第25辆车车速在20 m/s上下小范围剧烈波动, 即车流不稳定, 与理论推导结果不一致。因此, 文中选择m=0.2为MVSSDSE-CM最优反馈增益。
|
图 1 不同m值下MVSSDSE-CM中第1辆车、第25辆车和第50辆车的速度变化曲线 Figure 1 The first, 25-th and 50-th vehicles' temporal velocity behaviors of MVSSDSE-CM under the different m |
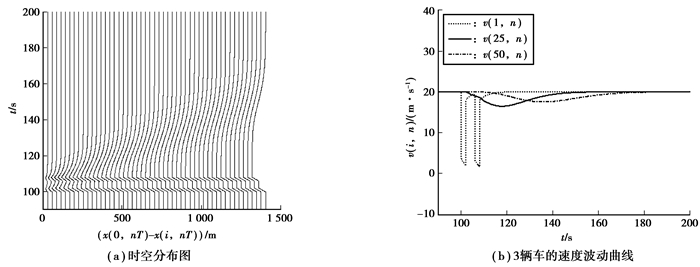
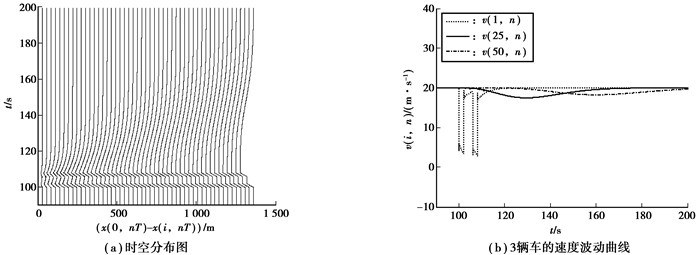
接下来更加细致地验证MVSSDSE-CM对拥堵的抑制性能, 同样使头车在100 s和106 s处分别停止3 s[10]来观察交通系统运行状态。图 2, 图 3分别给出了ITS-CM和MVSSDSE-CM的车辆时空分布图以及对应的第1辆车、第25辆车和第50辆车速度波动情况。
|
图 2 ITS-CM中头车突然停止2次, 整个车流运行状态的数值仿真图 Figure 2 The leading vehicle stops two times suddenly in ITS-CM, the Numerical simulations of the traffic flow's running state |
|
图 3 MVSSDSE-CM中头车突然停止2次, 整个车流运行状态的数值仿真图 Figure 3 The leading vehicle stops two times suddenly in MVSSDSE-CM, the Numerical simulations of the traffic flow's running state |
从图 2(a)和3(a)对比可以看出:2幅图中车头间距波动均较小, 无晶振现象, 但图 3(a)中交通拥堵抑制效果更好, 车头间距扰动向上游区域传播, 能更快地恢复到稳定状态。对比图 2(b)和3(b)可以发现:ITS-CM和MVSSDSE-CM中3辆车的车速均在20 m/s两侧波动, 但图 3(b)中3辆车的速度波动明显比图 2(b)中的要小, 整个车流系统的稳定性能得到进一步提升。仿真结果表明, 文中提出的MVSSDSE-CM较ITS-CM更能降低了拥堵的影响范围, 使得车流恢复稳定状态能力更强。
4 结论在ITS-CM的基础上, 引入多车稳态期望速度效应, 提出了一种新的拥堵控制跟驰模型即MVSSDSE-CM。运用线性控制理论, 得到交通系统保持稳定的临界条件。最后, 通过仿真验证了多车稳态期望速度效应能够进一步提升交通系统的稳定性能, 对拥堵的抑制性能更优。此后, 论文将采集实际交通数据对该模型进行参数辨识, 进一步改进模型, 以期提高模型对实际交通拥堵现象的模拟能力和抑制能力。
附录A
首先, 根据Jury稳定性判据, 如果多项式Pi(z)满足下列条件
| $ \left\{ \begin{array}{l} 1 + {a_i} + {b_i} > 0,\\ 1 - {b_i} > 0,\\ 1 - {a_i} + {b_i} > 0, \end{array} \right. $ | (A1) |
那么多项式Pi(z)是稳定的。求解不等式(A1), 得到:
| $ \begin{array}{l} {a_i}{r_i}{T^2} - {a_i}T < k < \frac{{4 - 2{\alpha _i}T + {a_i}{r_i}{T^2}}}{2},\\ 0 < {a_i}{r_i}{T^2} < 2。\end{array} $ | (A2) |
其次, 考虑无穷范数不等式‖Gi(z)‖∞≤1, 即
| $ {\left\| {{G_i}\left( z \right)} \right\|_\infty } = \mathop {\max }\limits_{\left| z \right| = 1} \left| {\frac{{\left[ { - m\left( {z - 1} \right),{k_1}\left( {z - 1} \right) + {a_i}{r_i}{T^2},{k_2}\left( {z - 1} \right), \cdots ,{k_s}\left( {z - 1} \right)} \right]}}{{{P_i}\left( z \right)}}} \right| \le 1。$ | (A3) |
令z=cosθ+i sin θ, 不等式(A3)变为
| $ \begin{array}{l} 2{m^2} - 2{m^2}\cos \theta - 2{k_1}{\alpha _i}{r_i}{T^2} + 2{k_1}{\alpha _i}{r_i}{T^2}\cos \theta + \left( {_i^\alpha {r_i}{T^2}} \right)2 + 2k_1^2 - 2k_1^2\cos \theta + \\ 2\sum\limits_{l = 2}^s {k_l^2} - 2\sum\limits_{l = 2}^s {k_l^2\cos \theta } \le 1 + 2{a_i}\cos \theta + 4{b_i}{\left( {\cos \theta } \right)^2} - 2{b_i} + 2{a_i}{b_i}\cos \theta + a_i^2 + b_i^2。\end{array} $ | (A4) |
将(A4)化简后, 可得
| $ \begin{array}{l} 2\left( {1 - \cos \theta } \right)\left[ { - \sum\limits_{l = 2}^s {k_l^2 - {m^2}} + {k_1}{\alpha _i}{r_i}{T^2} + 2\left( { - 1 + {\alpha _i}T + k - {\alpha _i}{r_i}{T^2}} \right)\cos \theta + 2 + {k^2} - } \right.\\ \left. {2{\alpha _i}T + \left( {_i^\alpha T} \right)2 - \alpha _i^2{r_i}{T^3} - k\left( {2 - 2{\alpha _i}T + {\alpha _i}{r_i}{T^2}} \right)} \right] \ge 0。\end{array} $ | (A5) |
因为1-cosθ≥0, 对于任意的θ∈[0, 2π], 所以式(A5)可写为
| $ \begin{array}{l} - \sum\limits_{l = 2}^s {k_l^2 - {m^2}} + {k_1}{\alpha _i}{r_i}{T^2} + 2\left( { - 1 + {\alpha _i}T + k - {\alpha _i}{r_i}{T^2}} \right)\cos \theta + 2 + {k^2} - \\ 2{\alpha _i}T + \left( {_i^\alpha T} \right)2 - \alpha _i^2{r_i}{T^3} - k\left( {2 - 2{\alpha _i}T + {\alpha _i}{r_i}{T^2}} \right) \ge 0。\end{array} $ | (A6) |
又因为|cosθ|≤1, 所以(A6)可以分为3种情况讨论。
情况1:当-1+αiT+k-αiriT2>0时, 有
| $ \begin{array}{l} - \sum\limits_{l = 2}^s {k_l^2 - {m^2}} + {k_1}{\alpha _i}{r_i}{T^2} - 2\left( { - 1 + {\alpha _i}T + k - {\alpha _i}{r_i}{T^2}} \right) + 2 + {k^2} - \\ 2{\alpha _i}T + \left( {_i^\alpha T} \right)2 - \alpha _i^2{r_i}{T^3} - k\left( {2 - 2{\alpha _i}T + {\alpha _i}{r_i}{T^2}} \right) \ge 0。\end{array} $ | (A7) |
情况2:当-1+αiT+k-αiriT2<0时, 有
| $ \begin{array}{l} - \sum\limits_{l = 2}^s {k_l^2 - {m^2}} + {k_1}{\alpha _i}{r_i}{T^2} + 2\left( { - 1 + {\alpha _i}T + k - {\alpha _i}{r_i}{T^2}} \right) + 2 + {k^2} - \\ 2{\alpha _i}T + \left( {_i^\alpha T} \right)2 - \alpha _i^2{r_i}{T^3} - k\left( {2 - 2{\alpha _i}T + {\alpha _i}{r_i}{T^2}} \right) \ge 0。\end{array} $ | (A8) |
情况3:当-1+αiT+k-αiriT2=0时, 有
| $ \begin{array}{l} - \sum\limits_{l = 2}^s {k_l^2 - {m^2}} + {k_1}{\alpha _i}{r_i}{T^2} + 2 + {k^2} - 2{\alpha _i}T + \left( {_i^\alpha T} \right)2 - \alpha _i^2{r_i}{T^3} - \\ k\left( {2 - 2{\alpha _i}T + {\alpha _i}{r_i}{T^2}} \right) \ge 0。\end{array} $ | (A9) |
对于情况1, 综合考虑(A1)和(A2), 可求解得
| $ \begin{array}{l} 1 + {\alpha _i}{r_i}{T^2} - {\alpha _i}T < k < \frac{{4 - 2{\alpha _i}T + {\alpha _i}{r_i}{T^2}}}{2},\\ 0 < {\alpha _i}{r_i}{T^2} < 2。\end{array} $ | (A10) |
将
| $ \max \left\{ {1 - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2},{R_{11}}} \right\} < m < \frac{{4 - 2{\alpha _i}T - 2{k_1} + 2k + {\alpha _i}{r_i}{T^2}}}{2}。$ | (A11) |
这里
| $ \begin{array}{l} {R_{11}} = \frac{{4 - 4{\alpha _i}T + \alpha _i^2{T^2} + {k^2} - \alpha _i^2{r_i}{T^3} + 2{\alpha _i}{r_i}{T^2} - 2k}}{{{\alpha _i}T - 10/3}} + \\ \frac{{\left[ {\left( {4{\alpha _i}{r_i}{T^2} + 12k{\alpha _i}T - 2{k_1} - 6{\alpha _i}{r_i}{T^2}} \right)R/9 - \left( {\frac{2}{9} + \frac{1}{{{3^{s - 1}}}} + \sum\limits_{l = 2}^s {\frac{4}{{{3^{l + 1}}}}} } \right){R^2}} \right]1/2}}{{{\alpha _i}T - 10/3}}。\end{array} $ |
对于另外一个解,
| $ 1 - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2} < m < \min \left\{ {\frac{{4 - 2{\alpha _i}T + 2{k_1} - 2k + {\alpha _i}{r_i}{T^2}}}{2},{R_{12}}} \right\}, $ | (A12) |
这里
| $ \begin{array}{l} {R_{12}} = \frac{{4 - 4{\alpha _i}T + \alpha _i^2{T^2} + {k^2} - \alpha _i^2{r_i}{T^3} + 2{\alpha _i}{r_i}{T^2} - 2k}}{{{\alpha _i}T - 10/3}} - \\ \frac{{\left[ {\left( {4{\alpha _i}{r_i}{T^2} + 12k{\alpha _i}T - 2{k_1} - 6{\alpha _i}{r_i}{T^2}} \right)R/9 - \left( {\frac{2}{9} + \frac{1}{{{3^{s - 1}}}} + \sum\limits_{l = 2}^s {\frac{4}{{{3^{l + 1}}}}} } \right){R^2}} \right]1/2}}{{{\alpha _i}T - 10/3}}。\end{array} $ |
对于情况2, 综合考虑(A1)和(A2), 可求解得
| $ \begin{array}{l} {\alpha _i}{r_i}{T^2} - {\alpha _i}T < k < \min \left\{ {\frac{{4 - 2{\alpha _i}T + {\alpha _i}{r_i}{T^2}}}{2},{\alpha _i}{r_i}{T^2} - {\alpha _i}T + 1} \right\},\\ 0 < {\alpha _i}{r_i}{T^2} < 2。\end{array} $ | (A13) |
将
| $ \begin{array}{l} - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2} < m < \\ \min \left\{ {1 - {\alpha _i}T + {k_1} - k + {\alpha _i}{r_i}{T^2},\frac{{4 - 2{\alpha _i}T + 2{k_1} - 2k + {\alpha _i}{r_i}{T^2}}}{2},{R_{21}}} \right\}。\end{array} $ | (A14) |
这里
| $ \begin{array}{l} {R_{21}} = \frac{{4 - 4{\alpha _i}T + \alpha _i^2{T^2} + {k^2} - \alpha _i^2{r_i}{T^3} + 2{\alpha _i}{r_i}{T^2} - 2k}}{{{\alpha _i}T - 10/3}} - \\ \frac{{\left[ {\left( {2{\alpha _i}{r_i}{T^2} + 8k{\alpha _i}T - 2{k_1} - {\alpha _i}{r_i}{T^2}} \right)R/9 + \left( {\frac{2}{9} + \frac{1}{{{3^{s - 1}}}} + \sum\limits_{l = 2}^s {\frac{4}{{{3^{l + 1}}}}} } \right){R^2}} \right]1/2}}{{{\alpha _i}T - 10/3}}。\end{array} $ |
对于情况3, 综合考虑(A1)和(A2), 可求解得
| $ \max \left\{ { - {\alpha _i}T + {k_1} - \lambda + {\alpha _i}{r_i}{T^2},{R_{31}}} \right\} < m < \frac{{4 - 2{\alpha _i}T + 2{k_1} - 2\lambda + {\alpha _i}{r_i}{T^2}}}{2}, $ | (A15) |
这里
| $ \begin{array}{l} {R_{31}} = \frac{{4 - 4{\alpha _i}T + \alpha _i^2{T^2} + {k^2} - \alpha _i^2{r_i}{T^3} + 2{\alpha _i}{r_i}{T^2}}}{{{\alpha _i}T - 10/3}} + \\ \frac{{\left[ {2\left( {{\alpha _i}{r_i}{T^2} + 2k{\alpha _i}T - 2{k_1} - {\alpha _i}{r_i}{T^2}} \right)R/9 + \left( {\frac{2}{9} + \frac{1}{{{3^{s - 1}}}} + \sum\limits_{l = 2}^s {\frac{4}{{{3^{l + 1}}}}} } \right){R^2}} \right]1/2}}{{{\alpha _i}T - 10/3}}。\end{array} $ |
| [1] | Sun N, Fang Y, Chen H, et al. Amplitude-saturated nonlinear output feedback antiswing control for underactuated cranes with double-pendulum cargo dynamics[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 2135–2146. DOI:10.1109/TIE.2016.2623258 |
| [2] | Whitham G B. Exact solutions for a discrete system arising in traffic flow[J]. Philosophical Transactions of the Royal Society of London, 1990, 428: 4. |
| [3] |
周桐, 郑林江, 刘卫宁.
考虑预估驾驶行为的跟驰模型及其稳定性分析[J]. 重庆大学学报, 2016, 39(6): 141–147.
ZHOU Tong, ZHENG Linjiang, LIU Weining. A new car-following model with consideration of anticipation driving behavior and its stability analysis[J]. Journal of Chongqing University, 2016, 39(6): 141–147. DOI:10.11835/j.issn.1000-582X.2016.06.018 (in Chinese) |
| [4] | Zhou T, Sun D H, Li H, et al. A new coupled map car-following model considering drivers' steady desired speed[J]. Chinese Physics B, 2014, 5: 41–45. |
| [5] |
周桐, 李雨宣, 杨智勇, 等.
考虑车辆机械惯性的跟驰模型及其数值模拟分析[J]. 郑州大学学报(工学版), 2015, 36(4): 114–118.
ZHOU Tong, LI Yuxuan, YANG Zhiyong, et al. A new car following model with consideration of the vehicle's mechanical inertia effect and its analysis of numerical simulation[J]. Journal of Zhengzhou University(Engineering Science), 2015, 36(4): 114–118. (in Chinese) |
| [6] |
李修云, 周桐, 杨智勇.
基于最紧邻前车加速度信息的跟驰模型[J]. 重庆大学学报, 2015, 38(6): 153–158.
LI Xiuyun, ZHOU Tong, YANG Zhiyong. Car-following model based on the information of the nearest-neighbor leading car's acceleration[J]. Journal of Chongqing University, 2015, 38(6): 153–158. DOI:10.11835/j.issn.1000-582X.2015.06.021 (in Chinese) |
| [7] | Li Z, Li W, Xu S, et al. Traffic behavior of mixed traffic flow with two kinds of different self-stabilizing control vehicles[J]. Physica A, 2015, 436: 729–738. DOI:10.1016/j.physa.2015.05.090 |
| [8] | Xu X H, Pang J, Monterola C. Asymmetric optimal-velocity car following model[J]. Physica A, 2015, 436: 565–571. DOI:10.1016/j.physa.2015.04.023 |
| [9] | Bando M, Hasebe K, Nakayama A, et al. Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51(2): 1035–1042. DOI:10.1103/PhysRevE.51.1035 |
| [10] | Konishi K, Kokame H, Hirata K. Coupled map car-following model and its delayed-feedback control[J]. Physical Review E, 1999, 60: 4000–4007. DOI:10.1103/PhysRevE.60.4000 |
| [11] | Zhao X M, Gao Z Y. A control method for congested traffic induced by bottlenecks in the coupled map car-following model[J]. Physica A, 2006, 366: 513–522. DOI:10.1016/j.physa.2005.11.004 |
| [12] |
韩祥临, 姜长元, 葛红霞, 等.
基于智能交通系统的耦合映射跟驰模型和交通拥堵控制[J]. 物理学报, 2007, 56(8): 4383–4392.
HAN Xianglin, JIANG Changyuan, GE Hongxia, et al. A modified coupled map car-following model based on application of intelligent transportation system and control of traffic congestion[J]. Acta Physica Sinica, 2007, 56(8): 4383–4392. DOI:10.7498/aps.56.4383 (in Chinese) |
| [13] | Shen F Y, Ge H X, Zhang H, et al. A control method for congested traffic in the coupled map car-following model[J]. Chinese Physics B, 2009, 18(10): 4208–4215. DOI:10.1088/1674-1056/18/10/021 |
| [14] | Ge H X, Meng X P, Ma J, et al. An improved car-following model considering influence of other factors on traffic jam[J]. Physics Letters A, 2012, 377: 9–12. |
| [15] | Cheng R J, Han X L, Lo S M, et al. A control method applied to mixed traffic flow for the coupled-map car-following model[J]. Chinese Physics B, 2014, 23(3): 193–200. |
| [16] | Ge H X, Dai S Q, Dong L Y, et al. Stabilization effect of traffic flow in an extended car-following model based on an intelligent transportation system application[J]. Physical Review E, 2004, 70(2): 066134. |
 2018, Vol. 41
2018, Vol. 41

