为解决能源问题和环境问题,电动汽车已经受到了越来越多的关注。此外,从汽车动力学控制的角度,采用轮毂电机驱动的电动汽车与传统的内燃机汽车相比,还具以下优势[1]:轮毂电机驱动电动汽车每个车轮都可以安装轮毂电机且能独立驱动,车轮的驱动/制动力矩响应快速准确,同时电机的输出力矩也便于测量[2]。这些优点为电动汽车的横摆力矩控制带来了新的机遇。传统的直接横摆力矩控制(DYC, direct yaw moment control)通常采用差别制动的方式实现,这会导致车速明显降低,在某些时候不符合驾驶员的操纵意图,而分布式电动车可以采用制动驱动综合的DYC系统,能使车速在不明显下降的情况下提高汽车的操稳性。
目前,大部分直接横摆力矩控制均采用分层控制结构[3]。上层控制器用于决策出广义横摆力矩。文献[4]基于滑模控制理论设计了四轮驱动电动汽车的横摆力矩控制器,但滑模控制不可避免的抖振会影响车辆的舒适度。文献[5]设计了模糊PI控制器计算差动转矩,并进行了硬件在环仿真,验证了算法的有效性,但模糊规则的制定需要大量的专家经验。下层控制器用于分配广义横摆力矩。目前,基于优化理论的分配方法最为常见。文献[6]为最小化实际力和广义力误差,最小化控制量和最小化轮胎利用率,提出了一种新的目标函数,并设计了3个目标的权重调整规则,仿真结果表明该控制分配算法能保证电动汽车在不同工况下的操稳性。
由于实际应用中各个执行器必然存在约束,上述控制算法缺乏对约束的处理,有时会造成控制效果变差,而模型预测控制(MPC, model predictive control)因能解决在约束情况下的实时优化控制而受到广泛关注。文献[7]设计了针对主动转向的线性时变模型预测控制器,仿真验证了该低阶控制器能取得相对满意的控制效果且便于实际应用。文献[8]设计了基于非线性模型预测控制理论的主动前轮转向和四轮差动制动的集成控制器,仿真结果表明控制器能使汽车跟踪理想路径,但由于必须求解非线性规划问题,会使控制器运算负担过大,且控制器参数不易调整。
对于快速采样且对稳定性要求高的汽车控制系统,传统的模型预测控制要保证良好的稳定性必须选取更长的预测时域,这会增加控制器的计算负担。针对后轮轮毂电机驱动电动汽车设计其横摆力矩分层控制器。其中,上层为附加横摆力矩决策层,设计了基于拉盖尔函数的模型预测控制器,该控制器可以处理较大预测时域的控制问题,并且提高系统的动态响应性能。下层控制器通过求解二次规划问题将附加横摆力矩分配到两个后轮,使后轮轮胎利用率最低,从而提高车辆的稳定裕度。最后,对所设计的控制器进行了仿真,仿真结果表明:该控制器能根据驾驶员的期望跟踪理想横摆角速度,减小了汽车的动态响应时间和超调量,保证了汽车在低附着路面下的稳定性。
1 DYC控制结构文中采用的控制器结构如图 1所示。
|
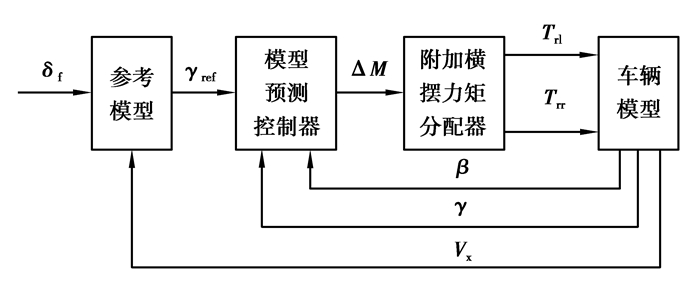
图 1 控制器结构 Figure 1 Controller structure |
控制器主要由4个部分组成,参考模型依据前轮转角δf及汽车的纵向车速Vx计算出理想的横摆角速度γref;模型预测控制器根据实际的横摆角速度γ、质心侧偏角β和理想横摆角速度计算得到附加横摆力矩ΔM;附加横摆力矩分配器将则将广义的横摆力矩分配为左后轮驱/制动力矩Trl和右后轮驱/制动力矩Trr,从而控制车辆的横摆运动。
2 参考模型正常情况下,驾驶员能够正确操作处于线性区域的车辆,而当汽车处于非线性区时,驾驶员往往不能对汽车做出正确的操作。为改善驾驶员对车辆非线性区的不适应,降低操作难度,因此采用线性二自由度汽车模型作为直接横摆力矩控制的参考模型。根据参考模型,理想横摆角速度是驾驶员转向输入的稳态增益,由文献[9]有:
| $ {\gamma _{{\rm{ref}}}} = {V_{\rm{x}}}{\delta _{\rm{f}}}/\left[{L\left( {1 + K{V_{\rm{x}}}^2} \right)} \right], $ | (1) |
式中:Vx为车辆的纵向车速;δf为前轮转角;K为稳定性因数,
由于侧向加速度不能超过路面附着能力,故理想横摆角速度还必须满足
| $ \left| {{\gamma _{{\rm{ref}}}}} \right| \le \left| {\mu g/{V_{\rm{x}}}} \right|, $ | (2) |
式中:μ为路面附着系数;g为重力加速度。
因此,由式(1)和式(2)得到理想横摆角速度
| $ {\gamma _{{\rm{ref}}}} = \min \left\{ {\left| {{V_{\rm{x}}}{\delta _{\rm{f}}}/\left[{L\left( {1 + K{V_{\rm{x}}}^2} \right)} \right]} \right|, \left| {\mu g/{V_{\rm{x}}}} \right|} \right\}{\rm{sign}}\left( {{\delta _{\rm{f}}}} \right)。$ | (3) |
预测模型采用带附加横摆力矩的状态空间模型:
| $ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = {\mathit{\boldsymbol{A}}_0}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{B}}_0}u + {\mathit{\boldsymbol{E}}_0}{\delta _{\rm{f}}}, \\ \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{C}}_0}\mathit{\boldsymbol{x}}, \end{array} $ | (4) |
式中:x=[β γ]T为车辆状态,其中横摆角速度可以通过传感器获得,质心侧偏角通过设计状态观测器也可获得;y为横摆角速度输出;u=ΔM,为附加横摆力矩;
模型预测控制常用于离散控制,此外,式(4)中前轮转角δf可视为固定干扰略去,因此将式(4)离散化并改写成增量型形式:
| $ \begin{array}{l} \Delta {\mathit{\boldsymbol{x}}_{\rm{G}}}\left( {k + 1} \right) = {\mathit{\boldsymbol{A}}_{\rm{G}}}\Delta {\mathit{\boldsymbol{x}}_{\rm{G}}}\left( k \right) + {\mathit{\boldsymbol{B}}_{\rm{G}}}\Delta u\left( k \right), \\ \mathit{\boldsymbol{y}}\left( {k + 1} \right) = {\mathit{\boldsymbol{C}}_{\rm{G}}}\Delta {\mathit{\boldsymbol{x}}_{\rm{G}}}\left( {k + 1} \right) + \mathit{\boldsymbol{y}}\left( k \right), \end{array} $ | (5) |
式中:ΔxG(k)=[Δβ(k) Δγ(k)]T;Δβ(k)、Δγ(k)分别为质心侧偏角和横摆角速度增量;y(k)为离散化后的输出量;Δu为控制增量;AG、BG、CG分别为A0、B0、C0离散化后的矩阵。
选取[ΔxG(k) y(k)]T为新状态变量,改写式(5)得到:
| $ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \mathit{\boldsymbol{B}}\Delta u\left( k \right), \\ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right), \end{array} $ | (6) |
式中:
由于传统的模型预测控制采用一系列的脉冲算子来表达模型预测控制增量Δu,而汽车控制系统采样迅速,要得到更好地控制轨迹和稳定性往往需要更长的优化时域和更多的参数,这样会增大控制器的计算负担且系统数值解较差,故本文采用拉盖尔函数网络重新表示原系统的控制序列[10]。拉盖尔函数的z传递函数为
| $ {\mathit{\Gamma }_p}\left( z \right) = \frac{{\sqrt {{{\left( {1 - a} \right)}^2}} }}{{z - a}}{\left[{\frac{{1-az}}{{z-a}}} \right]^{p - 1}}, $ | (7) |
式中:Γp(z)为离散的拉盖尔函数;p=1, 2, …, N为拉盖尔函数阶数;a为拉盖尔函数的极点,其取值范围为0≤a<1;z为z变换中的变量。
离散的拉盖尔函数在时域内可用z反变换求得
| $ {l_p}\left( k \right) = {z^{ - 1}}\left\{ {{\mathit{\Gamma }_p}\left( z \right)} \right\}, $ | (8) |
式中:lp(k)为k时刻离散拉盖尔函数的时域表示。
根据式(7),一组离散的拉盖尔函数满足差分方程
| $ \mathit{\boldsymbol{L}}\left( {k + 1} \right) = {\mathit{\boldsymbol{A}}_{\rm{q}}}\mathit{\boldsymbol{L}}\left( k \right), $ | (9) |
式中:L(k)=[l1(k) l2(k) … lN(k)]T;L(k+1)=[l1(k+1) l2(k+1) … lN(k+1)]T;
当k=0时,可计算得到拉盖尔函数的值
| $ \mathit{\boldsymbol{L}}{\left( 0 \right)^{\rm{T}}} = \sqrt {{{\left( {1 - a} \right)}^2}} \left[{\begin{array}{*{20}{c}} 1&{-a}&{{a^2}}&{-{a^3}}& \cdots &{{{\left( {-1} \right)}^{N - 1}}{a^{N - 1}}} \end{array}} \right]。$ |
根据文献[11],假设当前时刻为k0,则在k个时刻后的控制增量可以用拉盖尔函数网络表示为
| $ \Delta u\left( {{k_0} + k} \right) \approx \sum\limits_{j = 1}^N {{c_j}\left( {{k_0}} \right){l_j}\left( k \right)}, $ | (10) |
即:
| $ \Delta u\left( {{k_0} + k} \right) \approx \mathit{\boldsymbol{L}}{\left( k \right)^{\rm{T}}}\mathit{\boldsymbol{\eta }}, $ | (11) |
式中:Δu(k0+k)=u(k0+k)-u(k0+k-1),为控制增量;N为拉盖尔函数项数;η=[c1 x2 … cN]T,cj为常数,j=1, 2, …, N。
通过这种变换,就可以将传统的控制时域Nc用参数a和N表示。同时,在更长预测时域的情况下,通过选取合适的a和N可以优化系统的动态响应,克服了传统模型预测控制必须使用庞大的数据矩阵的缺点,从而降低计算量。经过试验,文中选择a=0.9,N=2。
由式(6)和式(11),在第m个时刻,系统的状态和输出为
| $ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {{k_0} + m\left| {{k_0}} \right.} \right) = {\mathit{\boldsymbol{A}}^m}\mathit{\boldsymbol{x}}\left( {{k_0}} \right) + \mathit{\boldsymbol{\varphi }}{\left( m \right)^{\rm{T}}}\mathit{\boldsymbol{\eta }}, \\ \mathit{\boldsymbol{y}}\left( {{k_0} + m\left| {{k_0}} \right.} \right) = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^m}\mathit{\boldsymbol{x}}\left( {{k_0}} \right) + \mathit{\boldsymbol{C\varphi }}{\left( m \right)^{\rm{T}}}\mathit{\boldsymbol{\eta }}, \end{array} $ | (12) |
式中:x(k0)为k0时刻的状态量;x(k0+m|k0)为k0+m时刻的状态量;y(k0+m|k0)为k0+m时刻的输出;
传统MPC的目标函数为
| $ J = \sum\limits_{m = 1}^{{N_{\rm{p}}}} {\left\| {y\left( {{k_0} + m\left| {{k_0}} \right.} \right) - r\left( {{k_0} + m} \right)} \right\|_\mathit{\boldsymbol{Q}}^2} + \sum\limits_{m = 0}^{{N_{\rm{p}}} - 1} {\left\| {\Delta u\left( {{k_0} + m} \right)} \right\|_\mathit{\boldsymbol{R}}^2}, $ | (13) |
式中:Np为预测时域;r(k0+m)为k0+m时刻的期望输出;Δu(k0+m)为k0+m时刻的输入增量;Q,R均为权重矩阵,文中Q取为单位矩阵,R取为零矩阵。
当预测时域Np足够大时,拉盖尔函数具有正交的性质:
| $ \begin{array}{l} \sum\limits_{m = 0}^{{N_{\rm{p}}} - 1} {{l_s}\left( m \right){l_t}\left( m \right)} = 0, s \ne t;\\ \sum\limits_{m = 0}^{{N_{\rm{p}}} - 1} {{l_s}\left( m \right){l_t}\left( m \right)} = 1, s = t。\end{array} $ | (14) |
由式(11)和式(14)可将目标函数改写为
| $ J = \sum\limits_{m = 1}^{{N_{\rm{p}}}} {\left\| {y\left( {{k_0} + m\left| {{k_0}} \right.} \right) - r\left( {{k_0} + m} \right)} \right\|_\mathit{\boldsymbol{Q}}^2} + {\mathit{\boldsymbol{\eta }}^{\rm{T}}}{\mathit{\boldsymbol{R}}_{\rm{L}}}\mathit{\boldsymbol{\eta }}, $ | (15) |
式中:RL=R,取为零矩阵。
将式(12)带入式(15),并求解方程∂J/∂η=0可得:
| $ \eta = - {\left( {\sum\limits_{m = 1}^{{N_{\rm{p}}}} {\mathit{\boldsymbol{\varphi }}\left( m \right)\mathit{\boldsymbol{Q\varphi }}{{\left( m \right)}^{\rm{T}}}} + {\mathit{\boldsymbol{R}}_{\rm{L}}}} \right)^{ - 1}}\left( {\sum\limits_{m = 1}^{{N_{\rm{p}}}} {\mathit{\boldsymbol{\varphi }}\left( m \right)\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^m}\mathit{\boldsymbol{x}}\left( {{k_0}} \right) - r\left( {{k_0} + m} \right)} \right)} } \right), $ | (16) |
定义
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \left( {\sum\limits_{m = 1}^{{N_{\rm{p}}}} {\mathit{\boldsymbol{\varphi }}\left( m \right)\mathit{\boldsymbol{Q\varphi }}{{\left( m \right)}^{\rm{T}}}} + {\mathit{\boldsymbol{R}}_{\rm{L}}}} \right), $ | (17) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = \left( {\sum\limits_{m = 1}^{{N_{\rm{p}}}} {\mathit{\boldsymbol{\varphi }}\left( m \right)\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^m}\mathit{\boldsymbol{x}}\left( {{k_0}} \right) - r\left( {{k_0} + m} \right)} \right)} } \right), $ | (18) |
因此
| $ \mathit{\boldsymbol{\eta }} = - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}, $ |
由于仅第一个控制量作用于系统,故
| $ \Delta u\left( {{k_0}} \right) = \mathit{\boldsymbol{L}}{\left( 0 \right)^{\rm{T}}}\mathit{\boldsymbol{\eta }}。$ | (19) |
实际应用中,附加横摆力矩的大小和增量均存在约束,其约束条件为
| $ \Delta {u_{\min }} \le \Delta u\left( {{k_0}} \right) \le \Delta {u_{\max }}, $ | (20) |
| $ {u_{\min }} \le u\left( {{k_0}} \right) \le {u_{\max }}。$ | (21) |
为减轻运算负担,仅对控制序列的第一个量引入约束。将式(20)和式(21)用拉盖尔函数的形式表示为
| $ \Delta {u_{\min }} \le \mathit{\boldsymbol{L}}{\left( 0 \right)^{\rm{T}}}\mathit{\boldsymbol{\eta }} \le \Delta {u_{\max }}, $ | (22) |
| $ {u_{\min }} \le \mathit{\boldsymbol{L}}{\left( 0 \right)^{\rm{T}}}\mathit{\boldsymbol{\eta }} + u\left( {{k_0} - 1} \right) \le {u_{\max }}。$ | (23) |
当求解得到的控制量超出约束时,需要重新求解由目标函数式(15)和约束条件式(22)和式(23)构成的二次规划问题得到新的控制量。
4 附加横摆力矩分配器设计由上层控制器计算得到广义控制量需要分配为左后轮和右后轮轮毂电机的驱动或制动力矩。根据车辆动力学,左后轮力矩Trl和右后轮力矩Trr需满足
| $ \Delta M = \frac{d}{2}\left( { - {F_{{\rm{xrl}}}} + {F_{{\rm{xrr}}}}} \right), $ | (24) |
| $ {F_{{\rm{xrl}}}} = \frac{{{T_{{\rm{rl}}}}}}{r}, $ | (25) |
| $ {F_{{\rm{xrr}}}} = \frac{{{T_{{\rm{rr}}}}}}{r}, $ | (26) |
式中:Fxi(i=rl, rr)为轮胎纵向力;d为后轮轮距;r为轮胎的有效滚动半径。
根据文献[12],引入轮胎负荷率指标
| $ {\xi _i} = \sqrt {F_{{\rm{x}}i}^2 + F_{{\rm{y}}i}^2} /\left( {{\mu _{\max }}{F_{{\rm{z}}i}}} \right), $ | (27) |
式中:ξi为轮胎利用率;Fyi为轮胎侧向力;Fzi为轮胎垂直载荷;μmax为最大路面附着系数。
式(27)中轮胎利用率越小,说明能利用的轮胎力越大,车辆也越稳定。由于横摆力矩控制无法对侧向力Fyi进行直接控制,因此,侧向力Fyi将不作为优化问题的求解量,而是通过状态观测器直接获取。考虑轮胎附着约束与执行器约束,同时联立式(24)~式(27),可将附加横摆力矩分配问题转化为下列二次规划问题:
| $ \begin{array}{*{20}{c}} {\min f = F_{{\rm{xrl}}}^2/{{\left( {{\mu _{\max }}{F_{{\rm{zrl}}}}} \right)}^2} + F_{{\rm{xrr}}}^2/{{\left( {{\mu _{\max }}{F_{{\rm{zrr}}}}} \right)}^2}, }\\ {s.t.\;\;\;\;\Delta M = d\left( { - {F_{{\rm{xrl}}}} + {F_{{\rm{xrr}}}}} \right)/2, }\\ {{F_{{\rm{x}}i}} = {T_i}/r, }\\ {F_{{\rm{x}}i}^2 + F_{{\rm{y}}i}^2 \le {{\left( {{\mu _{\max }}{F_{{\rm{z}}i}}} \right)}^2}, }\\ {{T_{\min }} \le {T_i} \le {T_{\max }}, } \end{array} $ | (28) |
式中:Tmin为最大制动力矩;Tmax为最大驱动力矩。
通过求解二次规划问题则可得到左后轮和右后轮需要的力矩。
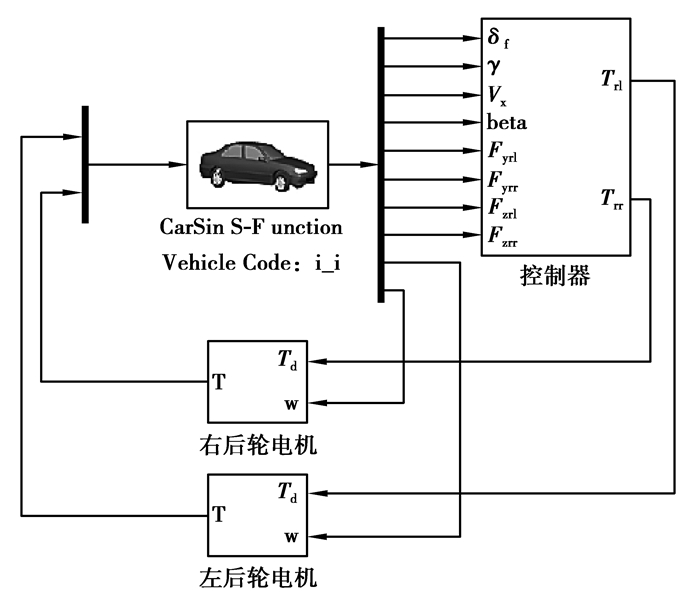
5 仿真分析为验证上述控制算法,利用Carsim与Matlab/Simulink搭建了仿真平台,如图 2所示。选择前轮转角阶跃输入和驾驶员闭环的紧急双移线2种工况作为试验工况。
|
图 2 联合仿真框图 Figure 2 Joint simulation block diagram |
采用Carsim的A级车稍加修改作为试验车辆,其主要参数见表 1。
| 表 1 车辆参数 Table 1 Vehicle parameters |
选择更大的预测时域能保证控制的稳定性,综合考虑控制的稳定性和快速性且经过反复试验后,选择Np=100。对于高附着系数和低附着系数2种路面工况,汽车轮胎的力学特性会发生变化,故2种仿真工况的约束条件有所不同,其数值参见表 2。
| 表 2 2种工况的约束条件 Table 2 Constraints of two conditions |
车辆以72 km/h的速度行驶1 s后,前轮转角阶跃输入3°路面附着系数为0.75,采样时间为0.01 s。其仿真结果如图 3所示。

|
图 3 前轮转角阶跃输入仿真结果 Figure 3 Simulation results of front wheel step steer input |
图 3(a)表示前轮转角输入。从图 3(b)可以看出,未施加控制车辆的横摆角速度大于理想横摆角速度,而在施加控制之后,车辆的横摆角速度超调量明显减小,且在1.5 s左右即达到稳态值,反应时间明显减小,说明该控制器提高了汽车瞬态反应性能。图 3(c)显示了车辆的质心侧偏角响应,由于质心侧偏角未作为控制目标,所以控制器无法跟踪由线性二自由度模型得出的理想质心侧偏角[13],但施加了控制的车辆质心侧偏角仍明显小于未施加控制的车辆。图 3(d)表示上层控制器输出的附加横摆力矩。图 3(e)表示左右轮的输出转矩,该图表明,通过二次规划法设计的附加横摆力矩分配器能够充分利用载荷较大轮胎的附着力。图 3(f)表示后轮轮胎总利用率,可以看出轮胎总利用率在施加控制之后由1.5降到1.4,说明控制分配器能提高汽车的稳定裕度。
5.2 双移线仿真为验证在低附着路面上汽车的稳定性,选取车辆以72 km/h的速度,在路面附着系数为0.3的道路上进行紧急双移线试验。
其仿真结果如图 4所示。
|
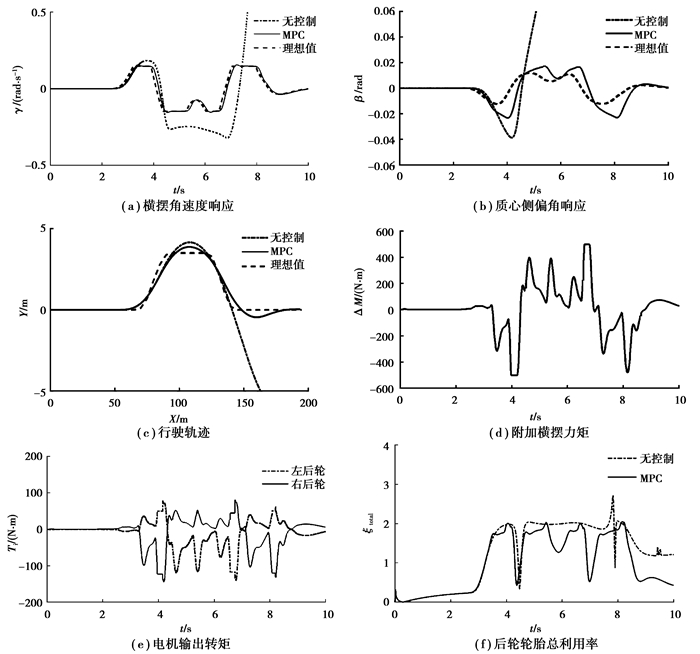
图 4 双移线仿真结果 Figure 4 Simulation results of double lane change |
从图 4(a)和图 4(b)的横摆角速度响应和质心侧偏角响应可以看出,在低附着路面下,未施加控制的汽车,从4.5 s开始汽车的横摆角速度和质心侧偏角迅速增大,汽车发生失稳,而在施加控制之后,汽车能够跟踪理想的横摆角速度值,且质心侧偏角与理想值的误差在允许范围内,保持了行驶的稳定性。图 4(c)显示了汽车的行驶轨迹,无控制的汽车在纵向位移150 m后侧向位移增大,汽车无法按照驾驶员的要求跟踪理想路径,说明此时汽车已发生严重侧滑,而施加控制之后汽车仍能稳定地跟踪理想的路径。图 4(d)是上层控制器输出的横摆力矩值,可以看到在4 s左右,控制器将附加横摆力矩限制在了-500 N·m,在6.8 s左右,控制器将附加横摆力矩限制在了500 N·m,从而避免了过大的附加横摆力矩输入到下层控制分配层,由此说明了上层控制器对约束的有效处理。图 4(e)是电机输出的力矩值,可以看出两者的变化趋势一致,左后轮和右后轮产生的横摆力矩方向一致。图 4(f)表示后轮轮胎总利用率,可以看出在4.5 s后无控制车辆的轮胎附着力达到了极限,而施加了控制的车辆仍有少部分余量,从而保持了车辆行驶的稳定性。
6 结论设计了基于拉盖尔函数模型预测理论和优化控制分配理论的直接横摆力矩分层控制器。相比于滑模控制、模糊控制等其他控制方法,该控制器能处理分布式电动汽车转向行驶中的各种约束。通过选取更长的预测时域,该控制器相比于传统的模型预测控制能在不增加计算量的前提下进一步保证汽车的稳定性。
| [1] | Hori Y. Future vehicle driven by electricity and control-research on four wheel motored UOT Electric March Ⅱ[J]. IEEE Transactions on Industrial Electronics, 2004, 51(5): 954–962. DOI:10.1109/TIE.2004.834944 |
| [2] | Ando N, Fujmoto H. Yaw-rate control for electric vehicle with active front/rear steering and driving/braking force distribution of rear wheels[C]//The 11th IEEE International Workshop on Advanced Motion Control, Nagaoka, Japan. 2010: 726-731. |
| [3] |
余卓平, 冯源, 熊璐.
分布式驱动电动汽车动力学控制发展现状综述[J]. 机械工程学报, 2013, 49(8): 105–114.
YU Zhuoping, FENG Yuan, XIONG Lu. Review on vehicle dynamics control of distributed drive electric vehicle[J]. Journal of Mechanical Engineering, 2013, 49(8): 105–114. (in Chinese) |
| [4] |
林程, 彭春雷, 曹万科.
独立驱动电动汽车稳定性的滑模变结构控制[J]. 汽车工程, 2015, 37(2): 132–138.
LIN Cheng, PENG Chunlei, CAO Wangke. Sliding mode variable structure control for the stability of independent drive electric vehicle[J]. Automotive Engineering, 2015, 37(2): 132–138. (in Chinese) |
| [5] |
许建, 张政, 李翔, 等.
独立驱动电动汽车横摆力矩的模糊控制算法[J]. 西安交通大学学报, 2014, 48(7): 83–89.
XU Jian, ZHANG Zheng, LI Xiang, et al. A fuzzy control system for the direct yaw moment of 4WD electric vehicles[J]. Journal of Xi'an Jiaotong University, 2014, 48(7): 83–89. DOI:10.7652/xjtuxb201407015 (in Chinese) |
| [6] | Li B, Goodarzi A, Khajepour A, et al. An optimal torque distribution control strategy for four-independent wheel drive electric vehicles[J]. Vehicle System Dynamics, 2015, 53(8): 1172–1189. DOI:10.1080/00423114.2015.1028414 |
| [7] | Falcone P, Borrelli F, Asgari J, et al. Predictive active steering control for autonomous vehicle systems[J]. IEEE Transactions on Control System Technology, 2007, 15(3): 566–580. DOI:10.1109/TCST.2007.894653 |
| [8] |
杨建森, 郭孔辉, 丁海涛.
基于模型预测控制的汽车底盘集成控制[J]. 吉林大学学报(工学版), 2011(S2): 1–5.
YANG Jiansen, GUO Konghui, DING Haitao. Vehicle integrated chassis control based on model predictive control[J]. Journal of Jilin University (Engineering and Technology Edition), 2011(S2): 1–5. (in Chinese) |
| [9] |
韩家伟, 李以农, 陈瑶.
横摆力矩滑模控制的轮边驱动电动汽车稳定性分析[J]. 机械科学与技术, 2016, 35(9): 1414–1420.
HAN Jiawei, LI Yinong, CHEN Yao. Stability analysis of wheel-drive electric vehicle based on sliding mode control of yaw moment[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(9): 1414–1420. (in Chinese) |
| [10] | Wang L. Model predictive control system design and implementation using matlab[M]. New York: Springer, 2009. |
| [11] | Wang L. Discrete model predictive controller design using laguerre functions[J]. Journal of Process Control, 2004, 14(2): 131–142. DOI:10.1016/S0959-1524(03)00028-3 |
| [12] | Song P, Tomizuka M, Zong C F. A novel integrated chassis controller for full drive-by-wire vehicles[J]. Vehicle System Dynamics, 2015, 53(2): 215–236. DOI:10.1080/00423114.2014.991331 |
| [13] | Rajamani R. Vehicle dynamics and control[M]. New York: Springer, 2006. |
 2018, Vol. 41
2018, Vol. 41



