b. 重庆大学 软件学院, 重庆 400044;
c. 重庆大学 期刊社, 重庆 400044
b. School of Software Engineering, Chongqing University, Chongqing 400044, P. R. China;
c. Journals Department, Chongqing University, Chongqing 400044, P. R. China
随着互联网信息技术日新月异的蓬勃发展,社交APP逐渐成为新兴的交友方式,例如Twitter、Facebook、新浪网等。根据网络数据统计显示,使用在线社交网络(OSNs, online social networks)[1]的活跃用户迅速增长。数据表明,从2008年到2014年每月至少访问OSNs一次的用户量从41%增长到65%[2]。显而易见,人们通过在线社交网络分享个人兴趣爱好、日常活动信息等,已成为人们与好友交流的普遍方式。然而,在用户的信息不断地被分享、转载的过程中,这些信息可能携带大量的用户隐私内容,并且信息不易受资源所有者的控制。因此,OSNs的敏感信息防御和信息流控制已经成为人们关心的热点问题[3]。
为了较好地防止用户隐私信息泄漏,研究者们思考利用隐私保护策略和访问控制技术来防御隐私信息泄漏。但是,鉴于社交网络结点之间的复杂性和多样性,在线社交网络敏感信息防御面临着严峻的挑战。OSNs中重要工作之一便是寻找有效的好友间亲密关系度量方法,找到亲密关系和可访问资源之间的关联关系,从资源敏感度层面体现结点与邻居结点的亲密程度。亲密度数值越大,体现着用户结点间存在比较亲密的关系,邻居结点间可访问的资源更丰富;反之,说明用户与好友的关系比较疏远,可访问的敏感资源非常有限。随着在线社交网络的不断发展,越来越多的人喜欢在社交网络上发布信息以及分享转载他人的信息,如果用户隐私信息被邻居结点用户转发,用户结点间属性信息和授权访问资源信息面临泄露的风险。鉴于此情况,为建立良好的社交网络信息交流方式,提出有效的信息流传递范围控制机制是迫在眉睫的研究工作。
1 研究现状为降低社交网络隐私信息被泄露的风险和保护信息安全,研究者们提出了多种隐私保护技术。70年代初,Dalenius T[4]首次对数据隐私保护作出了详细解释,指出用户需要获得访问权限才能访问查询数据库,数据库的资源不能被无权用户访问,这种方式使得访问数据库资源得到有效限制。近年来,研究者提出了一系列针对关系型数据的隐私保护技术。其中,P. S等[5]在1998年提出了K-匿名(k-anonymity),保证数据集中任意记录与其他k-1条记录无法识别,从而达到数据记录实体不被识别的目的。但随着研究的不断深入,k-anonymity隐私保护技术在同质性攻击和背景知识攻击方面面临巨大的风险。Machanavajjhala A和Li N等相继发表了l-diversity[6]和t-closeness[7],这两种隐私保护技术都从概率角度出发,要求敏感信息的散落特点与均分分布类似,使结点隐私属性得到很好的保护。事实上,社交数据除了结点属性信息以外,还包括网络结点之间复杂的链接关系,传统社交网络隐私保护技术更多的考虑数据记录为二维表,数据记录之间的关联关系并没得到合理的考虑,社交网络用户结点间关联关系的保护机制缺乏。学者们相继提出符合社交数据隐私属性的结点K-匿名(k-anonymity)[8-9]、子图K匿名(k-automorphism)[10-12]、数据扰乱(data disruption)[13]、推演控制(deduction control)[14]等隐私保护方法。实践表明,上述隐私保护策略可以为隐私信息的数据发布提供有效保护,但在隐私信息流传递过程中,还不能为隐私信息提供适当的保护机制。
此外,访问控制策略也可适当保护用户隐私信息。策略约定在合法时间内,只有获得合法授权的用户才能访问系统资源,防止非法用户越权访问资源。2009年,Anwar等[15]阐述了Facebook的用户访问权限控制机制,并且通过形式化规范语言描述了Facebook的隐私保护策略,这是第一个基于真实社交网络抽象出来的访问控制机制。通过使用社交网络提供的服务,使用者可以便捷管理好友关系,组织好友开展网络社交活动,扩大朋友范围以及好友之间分享信息[16-17]。在此基础之上,文献[18]提出分析社交网络关系图,且关系图结点之间存在亲密度(intimacy),亲密度的量化通过可数字化的权重进行衡量,网络数据包的传递将根据结点之间亲密度选择分发。但是,该模型对亲密度的计算方式较为简单,用0或1刻画结点间亲密度缺少灵活性。在已有亲密度计算方式基础上,文献[19]假设对好友间分享不同敏感度信息发起隐私攻击,提出了一种基于社交网络好友亲密度等级的隐私保护模型(L-intimacy),该模型可一定程度上防止好友间发起的隐私攻击。然而,该模型只是将亲密度简单划分为4个等级,每个等级用数字刻画,并没给出具体算法如何衡量邻居结点间亲密度关系值。文献[20]提出一种基于好友亲密度的访问控制模型,该模型通过结合朴素贝叶斯算法,以此来求解请求访问资源者各种行为的权重,可推算出一个未知类别的用户结点被划分到明确类别结点的机率,并对明确类别中的用户结点按照大小关系排序,最后得到邻居结点间亲密度值大小关系。然而,在真实的社交网络情景下,用户邻居结点间互相访问资源的次数和访问行为并不涉及敏感隐私问题,存在隐私敏感问题的关注点是邻居结点间访问资源的敏感度。另外,利用Bell-LaPadulaon控制模型[21-23]的信息流传递划分多级安全域的思想,层级约束将会限制信息流从高安全等级向低安全等级传输信息。因此,从邻居结点间亲密关系角度思考寻找一种信息流传递范围控制方法,该方法与以往工作的不同之处在于以下几点:1)主要是根据结点允许邻居结点可访问资源的敏感度来衡量结点间的亲密关系,计算邻居结点亲密度的方法贴近利用敏感信息的敏感度来推算;2)将利用社交网络中邻居结点间的共同朋友数量来调整亲密度值,通过共同朋友数量来实现亲密度值跨越层级关系的目标;3)借鉴强制访问控制信息流的思想,对隐私信息流的传递结点进行安全等级划分,将信息流的传递限制在不同敏感等级范围内,实现敏感信息流的可控性传播。
2 亲密度计算模型 2.1 在线社交网络模型一般情形下,OSNs和线下社交网络是根据用户之间交友方式的不同进行分类。为对隐私风险概念进行合理解释,同离线社交网络中的敏感信息风险定义有所区分。社交网络用户结点可定义为:用户结点之间的访问行为、资源授权访问等行为均为在线社交网络情景下发生的行为,降低后续亲密度模型计算结果的不精准性。
对于任意一个在线社交网络,都可以借鉴图结构G=(V, A)的表述方式来抽象。其中,结点V表示社交网络中用户结点拥有的属性信息和用户结点已有的信息资源构成的二元组集合,用户集合表示为U={u1, u2, u3, …, un}。邻居结点之间信息资源的传递可以通过转载信息、浏览信息等方式完成,信息资源形式化描述为R={r1, r2, r3, …, rn}。详细说明,V={v1, v2, v3, …, vn}是由用户结点和所属资源形成的对应关系,集合中任意元素的形式化描述为vi={ui, Ri},ui为用户结点集合U的第i个用户结点,Ri表示用户ui持有各个敏感等级的资源集合。因此,网络中任意用户结点u拥有的资源可以表示为ru, j, 其中j∈{1, 2, 3, …, m}为网络中资源个数,资源表现形式可以是用户结点属性信息、用户结点间的链接关系信息以及邻居结点间授权访问资源等。
社交网络中用户结点之间信息流的传递需通过授权访问资源,实现好友间分享信息的目标。因此,用户的操作ai∈A集合定义为ai={ai, 1, ai, 2ai, 3…, ai, n},其中aj, x∈ai表示为aj, x=<ui, ruj, k, bn>,bn表示用户结点允许的资源访问行为(资源转发、信息查看)。元素aj, x代表用户结点uj允许邻居用户结点ui能够请求访问资源,并且可访问资源的敏感层次划分为k,同时允许进行bn类型的操作行为。笔者将k作为整数处理,根据整数排序结果划分资源敏感度的等级高低,即亲密度计算模型将资源敏感度等级划分为k层。比如,用户结点Alice将视频信息上传到社交网络上,同时授权邻居结点用户Bob拥有转载视频的权利,上述描述通过表达式可表示为<Alice, rBob, video, bn>。为描述亲密度模型提供铺垫,将bn大致划分为评论资源、转载资源以及浏览资源。
2.2 好友亲密度计算模型在通常离线社交网络情景下,人们彼此了解的基础上产生关联链接,亲密程度依据联系程度和联系内容发生变化,变化的过程伴随着隐私信息流的传递。以此推理,在线社交网络中,用户结点之间传递的信息流敏感度等级越高,则暗示着用户结点间可能存在较深的亲密关系。从社交网络管理者和维护者角度出发,笔者将用户结点编织的社交网络抽象为一张社交关系图,用户结点间的链接关系可理解为用户授予邻居结点可访问资源的权限。鉴于用户结点自身资源具有不同等级的敏感度,通过计算邻居结点间可访问资源的敏感度等级来衡量邻居结点的亲密程度。因此,亲密度可定义为:在线社交网络中,用户结点授予邻居结点在一段时间内可访问资源敏感度的刻画。
相邻结点好友的亲密度模型为
| $ I=(V, I_{\rm value}),$ | (1) |
其中:V是由用户结点和不同敏感度资源组成的二元关系集合;Ivalue代表的含义为邻居结点间亲密度的数值大小。Ivalue根据邻居结点间授权可访问资源的敏感度,通过资源敏感度和亲密度的等价转化关系,得到邻居结点间的亲密度计算方式,形式化描述为
| $ {I_{{\rm{value}}}} = \left\{ {{u_{{\rm{sub}}}}, {u_{{\rm{obj}}}}, \delta |{u_{{\rm{sub}}}}, {u_{{\rm{obj}}}} \in U, 0 \le \delta \le 1} \right\}, $ | (2) |
value描述为用户结点usub允许邻居结点uobj请求访问不同敏感等级的资源累积和。利用用户结点允许邻居结点请求查询或者转发资源的敏感程度来刻画邻居结点间的亲密关系,即邻居结点间可访问资源敏感度的概念与邻居结点间的亲密度值δ可等价转换,其中δ值越大,表明邻居结点间的亲密度高,结点授予邻居结点可访问资源的敏感度高或资源越多。
在线社交网络中,用户结点持有不同敏感程度的信息资源,为准确衡量用户结点间亲密关系,对用户结点资源进行敏感程度等级划分。假设用户所拥有资源的敏感级别有k个层次划分,最低敏感级别中每个资源的亲密度为cr1,每个敏感级别中资源的个数为β,邻居结点间亲密度形式化描述为
| $ \delta = {\beta _1}c{r_1} + {\beta _2}{\beta _1}c{r_1} + {\beta _3}{\beta _2}{\beta _1}c{r_1} \cdots, + {\beta _i}{\beta _{i-1}}{\beta _{i-2}}{\beta _{i-3, \cdots, }}{\beta _1}c{r_1}, 1 \le i \le k, $ | (3) |
假设上述计算公式恒等于1,求解等式得到最低敏感层其中一个资源的敏感度值,进而推算出每个资源敏感等级中资源的亲密度值,使得每个资源敏感等级层中的单个资源的亲密度值不会有越过层级关系的现象发生,这种处理方式使划分资源不同敏感等级层更有意义。
通常情景下的在线社交网络,仅从邻居结点间相互授权访问资源敏感度来刻画邻居结点间的亲密关系存在片面性。事实上,在线社交网络中邻居结点间共同朋友数量会对结点间的亲密关系产生巨大影响。文献[24]证实,当邻居节点间共同朋友数量达到某个数量时,可推算出用户与邻居结点之间存在敏感关系。因此,研究将邻居结点间相同好友数量作为亲密度计算模型的一个影响因子,以此来改进亲密关系值的计算方式,同时表示亲密度值的幅度变化,并且能够顺利越过层级限制的目的。文献[24]提出了邻居结点间相同朋友数量形式化表达式为
| $ {S_{{\rm{CN}}}}\left( {{u_i}, {u_j}} \right) = \left| {\mathit{\Gamma }\left( {{u_i}} \right) \cap \mathit{\Gamma }\left( {{u_j}} \right)} \right|, $ | (4) |
其中,用户ui的邻居结点集合为Γ(ui),邻居结点用户uj的邻居结点集合为Γ(uj),相同好友数量即为2个用户结点集合的交集。假设用户好友之间存在着授予可访问资源的链接,并且两者之间的共同朋友数量大于等于σ时,邻居结点间的亲密关系可以越过敏感信息的层级划分。因此,定义cr1为最低资源敏感等级划分层中单个资源的亲密度值,crk为最高资源敏感等级划分层中单个资源的亲密度值,F表示一个共同好友如何从最低敏感层影响变到最高敏感层
| $ \sigma \times F \times c{r_1} = c{r_k}, $ | (5) |
解等式得到F,便可用于对邻居结点间亲密度计算模型进行改进。
假设邻居结点间相同好友数量为σ时,将用户结点信息资源按照资源敏感等级划分为k层,计算跨越一层亲密度层级所需的共同好友数量
| $ {L_{{\rm{num}}}} = \sigma \div k, $ | (6) |
经过不断实验,可以寻找到一个比较合理的阈值,邻居结点间共同好友数量表现为哪些敏感层次的亲密度值计算受此阀值影响。假设用户结点ui和邻居结点uj的相同朋友数值是SCN,相同朋友数量能够增幅的敏感层数量为
| $ {L_n} = {S_{{\rm{CN}}}} \div {L_{{\rm{num}}}}, $ | (7) |
根据上述等式得出共同邻居数量影响的层级数,并对层级数范围内的亲密度值进行增幅计算。综上所述,邻居结点间的亲密度计算公式如下
| $ \begin{array}{l} C{R_{{\rm{value}}}} = {L_n} \times F \times {4_{{\rm{CN}}}} \times \\ \left( {{\beta _1}c{r_1} + {\beta _2}{\beta _1}c{r_1} + {\beta _3}{\beta _2}{\beta _1}c{r_1}, \cdots, + {\beta _n}{\beta _{n-1}}{\beta _{n-2}}{\beta _{n-3}}, \cdots, {\beta _1}c{r_1}} \right) + \\ {\beta _{n + 1}}{\beta _n}{\beta _{n - 1}}{\beta _{n - 2}}, \cdots, {\beta _1}c{r_1}, \cdots, + {\beta _k}{\beta _{k - 1}}{\beta _{k - 2}}{\beta _{k - 3}}, \cdots, \\ {\beta _1}c{r_1}, 1 \le n \le k, {L_n} = 1, \end{array} $ | (8) |
上述表达式Ln中, n表示共同好友数量增幅的亲密度层数,并依据该值对影响层的亲密度值进行增幅计算。当Ln为1说明共同邻居数量可以对第一层到第n层的资源进行增幅,但是,需要对增幅影响层的亲密度计算值进行约束,避免亲密度值大于第n+1层中的资源亲密度值,此计算方式充分体现了邻居结点间共同好友数量的增幅影响。超出共同好友数量增幅层级的亲密度计算方式维持不变,并将每层亲密度值相继叠加求和,推算出邻居结点间的亲密度值集合,算法2展示了亲密度值计算模型的详细步骤。
算法2 根据邻居结点授权可访问资源敏感度的亲密度算法
输入:邻居结点间的链接关系、用户结点授予邻居结点可访问资源的二元组集合
输出:用户结点和邻居结点间根据资源敏感度的亲密度值集合Ⅰ
1. for all ui∈Udo
2. for all uj∈Udo
3. if (ui, uj) exist edg
4. count (ui, uj)common friends=SCN(ui, uj)
5. Ln=SCN*k/σ
6. for cri ∈(ui, uj)
6. if Lcri<= Ln
7. I value += cri*F* SCN
8. if (I value > crn+1)
9. Ivalue= crn+1
10. else
11. Ivalue+= cri
12. end
13. return Ivalue
14. end
15. end
16. return I
经过对基于邻居结点亲密度计算模型的不断修正,邻居结点间的亲密关系可以得到比较合理的衡量。但是从社交网络管理者角度出发,邻居结点间的隐私信息流传递范围需得到有效控制,如何制定有效的信息流传递机制是值得深思的问题。
3 信息流访问控制为了防止社交网络中用户隐私信息被好友随意查看或者转载的现象发生,绝大多数社交网络服务商提供了基于角色的访问控制模型来控制用户间访问资源权限的问题。随着社交网络用户量不断增大,用户为好友分配访问权限的任务加重。然而,提出采用亲密度的方式限制好友的访问操作行为,依然无法控制敏感隐私信息流在不可信的用户结点间传递。
3.1 用户多级安全等级划分访问控制策略中的客体和主体可以是社交网络中任意用户结点。从请求访问者而言,用户结点和邻居结点之间存在主体和客体的相互转换关系。将借鉴安全等级划分思想对社交网络用户结点进行等级划分,以达到约束高安全等级信息流传递至低安全等级用户主体的目的。
借鉴MLS(MLS, mlsconstrain & mlsvalidatetrans)安全策略,认为社交网络中任意结点和邻居结点间存在一个根据亲密模型划分的敏感等级,该敏感等级可限制高安全等级的信息流不会传递到低安全等级用户。对于社交网络任意一个网络结点,设(sub1, obj1, r, a, L1inti)和(sub2, obj2, r, a, L2inti),若L1inti<L2inti,那么level(sub1, obj1)≤level(sub2, obj2)。采用MLS访问策略的社交网络,可在一定程度上有效防止邻居结点间信息流从高安全等级传递至低安全等级。
根据传统强制访问控制策略的特征,策略中明确规定了客体归属于哪个安全等级,此处安全等级指的是信息资源具有的隐私保护属性等级。根据在线社交网络的特点,将社交网络中的用户结点划分为多级客体敏感等级,用户与邻居结点间的亲密度存在客体敏感度等级区间ran(u),假设敏感等级为levelk,levelk(u)含义为社交网络中多级用户结点客体u授权邻居结点可访问资源的敏感等级,并且levelk(u)∈ran(u)。将借鉴安全等级划分思想来对隐私信息流传递范围进行有效控制。
3.2 敏感信息流的控制针对用户不能控制好友对自己隐私信息进行合理保护的问题,依据强制访问控制策略尝试制定社交用户结点间的安全等级划分规则,提出基于邻居结点间亲密度的多安全等级划分信息流控制机制
| $ \begin{array}{l} S\left( c \right) = \{ \left\langle \right.s, {o_{{\rm{resource}}}}, {i_{{\rm{resource}}}}, a, {i_{{\rm{ran}}}}\left( {s, o} \right)|s, o \in U,a \in\\ \left\{ {r, w} \right\}, {i_{{\rm{resource}}}}, {i_{{\rm{ran}}}}\left( {s, o} \right) \in \left[{0, 1} \right], {i_{{\rm{ran}}}}\left( {s, o} \right) \in {i_{{\rm{resource}}}}\left. \right\rangle \}, \end{array} $ | (9) |
其中s, oresource为主体用户结点s允许请问访问客体o的资源总数是oresource。根据s可访问资源数量得出2者之间的亲密度iran(s, o),取值范围为[0, 1]。社交网络维护者可根据信息流敏感等级计算出iresource,确定传递信息流所在资源敏感度等级,设置信息流传递可达范围。变量a为信息流传递过程中允许执行的操作(信息浏览、信息转载)。
4 实验结果及分析 4.1 实验环境设置基于邻接结点亲密度的信息流控制方法采用C++实现,在64位Windows 7平台上运行,处理器为Core i3-4150 3.5 GHz,内存大小为4 GB。在线社交网络用户数据通过利用Visul Studio 2015开发软件仿真模拟获取,实验随机模拟500个用户结点信息以及结点间的链接关系信息,生成过程中以不同概率的形式随机分配链接关系,使整个随机网络尽量符合真实在线社交网络场景。实验将随机生成资源的敏感级别设置为4个等级:非常敏感、敏感、一般、疏远。使在线社交网络中的每个用户以30%、25%、20%、15%的概率得到不同敏感级别的资源。
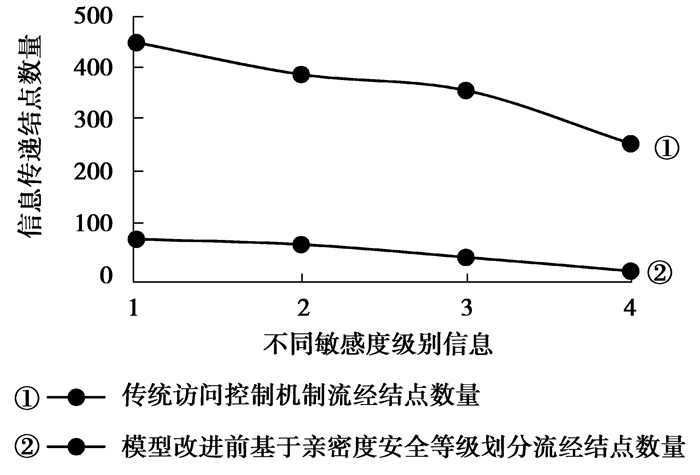
4.2 实验结果分析在没有引入邻居结点间共同好友数量影响因子的前提下,笔者率先提出基于邻居结点间根据授权访问资源敏感度计算亲密度的信息流控制模型,信息流经用户结点数量如图 1所示。图 1展示了在相同用户数量的条件下,对社交网络采取不同信息流传递隐私保护策略,不同敏感度级别的信息流传递经过的用户数量。从图 1观察得出,在传统访问控制策略下,用户结点发布的信息可以授权邻居结点操作访问权限,但是该隐私信息一旦被邻居结点转发,则该条隐私信息流的传递不受访问控制权限制约,信息可能在整个社交网络中传递。随着邻居结点间可访问资源的敏感等级不断提高,可访问资源的用户数量不断减少,但敏感资源的用户访问量却无法得到控制,传递中的隐私信息流受到极大的威胁。然而,在基于邻居结点亲密度的访问控制策略下,信息流传递需先判定是否有浏览或者转载权限,进而确定邻居结点间亲密度是否在信息流传递范围内,满足2个前提条件在社交网络中传递。从图 1观察可得结论:在基于邻居结点间亲密度访问控制策略下,用户隐私信息流传递的用户结点数量呈现明显下降趋势,为高低敏感等级的隐私信息提供良好的安全保障。
|
图 1 传统访问控制机制与亲密度信息流控制机制信息传递用户数量 Figure 1 Traditional access control mechanism and intimacy information flow control mechanism information transfer user numbers |
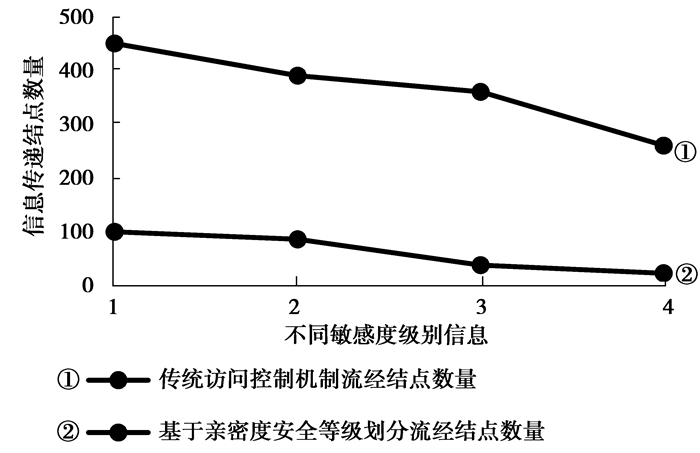
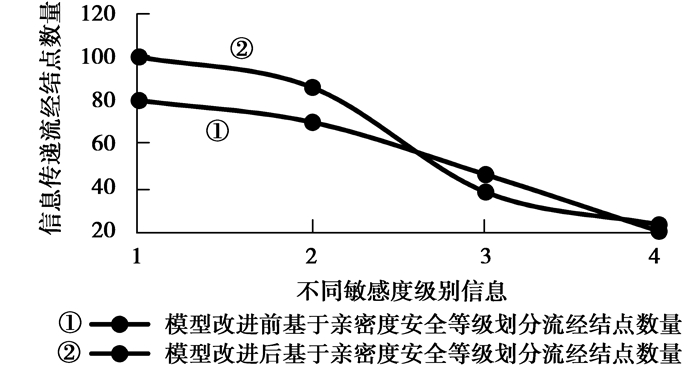
事实上,在线社交网络中存在非常多的因素会对亲密度值计算大小产生影响。在已有研究基础上,利用共同邻居数量作为计算亲密度值影响因子,最终基于邻居结点间亲密度的信息流控制算法实现结果如图 2所示。图 1和图 2观察表明,利用传统访问控制策略来限制隐私信息流在社交网络中传递的做法不太理想。从图 3可以看出,利用共同邻居数量对相应资源敏感等级层内的亲密度计算方式进行增幅操作,该操作虽扩大了低敏感度信息流传播用户结点数量,但却较好地控制较高等级信息流传递的用户结点数量。
|
图 2 传统访问控制机制与改进后亲密度信息流控制机制信息传递用户数量 Figure 2 Traditional access control mechanism and improved intimacy information flow control mechanism information transfer user numbers |
|
图 3 模型改进前后基于亲密度的信息流控制机制信息传递用户数量 Figure 3 Information flow control mechanism based on intimacy model improvement before and after |
针对在线社交网络中用户隐私信息流传递不可控制的问题,从在线社交网络管理者角度出发,构建了邻居结点的亲密度计算模型,该模型通过计算用户授予好友可访问资源的敏感度来衡量邻居结点的亲密关系。在此基础之上,借用MLS多安全等级划分的思想,利用亲密度模型计算值对社交网络中的用户结点进行多安全等级区域划分,提出了一种基于邻居结点亲密度的信息流控制机制。该机制用多级安全等级的思想对用户传递的隐私信息进行匹配,查看传递信息的亲密度是否在该安全等级允许的范围之内。该方法适用于在线社交网络的服务提供商,用户隐私信息的扩展程度将得到一定范围内的限制。
| [1] | Schneider F, Feldmann A, Krishnamurthy B, et al. Understanding online social network usage from a network perspe-ctive[C]//Proceeding of the ACM Sigcomm Conference on Internet Measurement. Chicago, VSA: IEEE, 2009: 35-48. |
| [2] | Heidemann J, Klier M, Probst F, et al. Online social networks:A survey of a global phenomenon[J]. Computer Networks, 2012, 56(18): 3866–3878. DOI:10.1016/j.comnet.2012.08.009 |
| [3] | Mo M Z, King I, Leung K S, et al. Empirical comparisons of attack and protection algorithms for online social netw-orks[J]. Procedia Computer Science, 2011, 5: 705–712. DOI:10.1016/j.procs.2011.07.092 |
| [4] | Dalenius T. Towards a methodology for statistical disclosure control[J]. Statistik Tidskrift, 1977, 15(2): 429–444. |
| [5] | Samarati P, Sweeney L. Protecting privacy when disclosing information:k-anonymity and its enforcement through generalization and suppression[J]. Technical report, SRI International, 1998, 32: 48–52. |
| [6] | Machanavajjhala A, Gehrke J, Kifer D, et al. L-diversity: privacy beyond k-anonymity[C]//International Conference on Data Engineering. Atlanta, USA: IEEE, 2006: 3. http://bioinformatics.oxfordjournals.org/external-ref?access_num=10.1145/1217299.1217302&link_type=DOI |
| [7] | Li N H, Li T CH. Suresh venkatasubramanian, t-closeness: privacy beyond k-anonymity and l-diversity[C]//International Conference on Data Engineering. Istanbul, Turkey: IEEE, 2007: 106-115. |
| [8] | Campan A, Traian M. A clustering approach for data and structural anonymity in social networks[J]. In Privacy, Security, and Trust in KDD Workshop in KDD, 2008: 33–54. |
| [9] | Hay M, Miklau G, Jensen D, et al. Resisting structural re-identification in anonymized social networks[J]. Vldb Journal, 2010, 19(6): 797–823. DOI:10.1007/s00778-010-0210-x |
| [10] | Zou L, Chen L, Zsu M T. K-automorphism:a general framework for privacy preserving network publication[J]. Proceedings of the Vldb Endowment, 2009, 2(1): 946–957. DOI:10.14778/1687627 |
| [11] | Cheng J, Fu W C, Liu J. K-isomorphism: privacy preserving network publication against structural attacks[C]//ACM SIGMOD International Conference on Management of Data, SIGMOD 2010. Indianapolis, Indiana: DBLP, 2010: 459-470. http://dl.acm.org/citation.cfm?id=1807218 |
| [12] | Zhou B, Pei J. Preserving privacy in social networks against neighborhood attacks[C]//International Conference on Data Engineering. Washington, DC, USA: IEEE, 2008: 506-515. http://dl.acm.org/citation.cfm?id=1547269 |
| [13] | Liu L, Wang J, Liu J, et al. Privacy preserving in social networks against sen-sitive edge disclosure[C]//Technical Report Technical Report CMIDA-HiPSCCS 006-08, Department of Computer Science. KY: IEEE, 2010: 32-35. |
| [14] | Liu X, Yang X. Protecting sensitive relationships against inference attacks in social networks[C]//International Conference on Database Systems for Advanced Applications. Busan, South Korea: Springer-Verlag, 2012: 335-350. http://link.springer.com/chapter/10.1007%252F978-3-642-29038-1_25 |
| [15] | Fong P W L, Anwar M, Zhao Z. A privacy preservation model for facebook-style social network systems[C]//Proceedings of the Computer Security-ESOTICS 2009. Berlin Heidelberg: Springer Verlag, 2009: 303-320. |
| [16] | Fogues R, Such J M, Espinosa A, et al. Open challenges in relationship-based privacy mechanisms for social network services[J]. International Journal of Human-Computer Interaction, 2015, 31(5): 350–370. DOI:10.1080/10447318.2014.1001300 |
| [17] |
严太华, 程映山, 李传昭, 等.
商业银行信用风险量化和管理模型的应用分析[J]. 重庆大学学报:自然科学版, 2004, 27(7): 109–113.
YAN Taihua, CHEN Yingshan, LI Chuanzhao, et al. The application analysis of credit risk quantification and management model of commercial banks[J]. Journal of Chongqing University(Natural Science Edition), 2004, 27(7): 109–113. (in Chinese) |
| [18] |
王恩, 杨永健, 赵卫丹, 等.
容迟网络中基于节点间亲密度的分组路由方法[J]. 通信学报, 2014, 35(12): 70–77.
WANG En, YANG Yongjian, ZHAO Weidan, et al. Packet-based routing algorithm in DTN based on the intimacy between nodes[J]. Journal on Communications, 2014, 35(12): 70–77. (in Chinese) |
| [19] |
陈伟鹤, 李文静, 朱江, 等.
基于社交网络好友攻击的位置隐私保护模型[J]. 计算机工程与科学, 2015, 37(4): 692–698.
CHEN Weihe, LI Wenjing, ZHU Jiang, et al. A model for protecting location privacy against attacks from friends in SNS[J]. Computer Engineering and Science, 2015, 37(4): 692–698. (in Chinese) |
| [20] | Zhai E. ISac:intimacy based access control for social network sites[J]. FIZ Karlsruhe Gmbh, 2012: 517–524. |
| [21] | Bayes R T. An essay toward solving a problem in the doctrine of chances[J]. Resonance, 2003, 8(4): 80–88. DOI:10.1007/BF02883540 |
| [22] | Bell D E, Lapadula L J. Secure computer systems:mathematical foundations[J]. Proceedings of the Computer Secilrity Formdations Workshop, 1973: 4–29. |
| [23] | Lapadula L J, Bell D E. Secure computer systems:a mathematical model[J]. Mitre Corp, 1973, 4: 229–263. |
| [24] | Liu X, Yang X. Protecting sensitive relationships against inference attacks in social networks[C]//International Conference on Database Systems for Advanced Applications. Busan, South Korea: Springer-Verlag, 2012: 335-350. http://link.springer.com/chapter/10.1007%252F978-3-642-29038-1_25 |
 2018, Vol. 41
2018, Vol. 41


 ,
,