轴承作为电机的重要部件之一,其运行工况直接影响整台电机的性能。在电机的故障种类中,轴承故障占所有电机故障的40%以上[1]。为了最大限度的挖掘轴承的工作潜力,减少或杜绝由轴承故障引起的事故,所以研究轴承故障诊断方法具有重要意义。电机轴承故障诊断关键技术包括信号预处理、故障特征提取和故障特征分类3部分。常用故障信号特征提取方法有局部均值分解[2-3](LMD, local mean decomposition)、经验模态分解[4-5] (EMD, empirical mode decomposition)等,但这两种特征提取方法都存在端点效应使结果失真的问题。常用特征分类方法有人工神经网络[6](ANN, artificial neural network)、决策树[7](DT, decision tree)等。但基于ANN的轴承故障诊断,不但需要大量的训练、测试样本,且学习速度慢、网络训练失败可能性较大;而DT易出现过拟合、忽略数据集中属性之间的相关性等问题。
小波包分析[8]能更加细分信号的高频部分,且能自适应选择相应频段;支持向量机[9](SVM)能解决小样本情况下的机器学习,避免过学习,且具有高泛化能力和避免局部极小点的优点。由于SVM性能取决于它的参数选择,蚁群算法[10](ACA, ant colony algorithm)、遗传算法[11](GA, genetic algorithm)等在优化参数时存在计算开销大与收敛速度较慢等问题,而粒子群优化[12](PSO)算法收敛速度快、精度高、可调参数少且简单易实现。
基于上述问题,提出了一种SVM与PSO相结合的特征分类方法。在特征提取阶段,充分考虑了故障严重程度对故障诊断的影响,将振动信号的时域无量纲特征参数和小波包能量值相结合,归一化后作为SVM的输入特征向量;然后构建SVM多分类器,并用PSO算法优化SVM的惩罚参数和RBF参数,提高故障诊断率。实验证明,在轴承的小样本故障诊断方法中,该方法相对于BP神经网络、决策树等算法有更高的分类准确率。
1 振动信号特征提取就轴承振动信号而言,从时域形式分析,只能检测出轴承是否有故障;从频域形式分析,既可识别出故障类型与故障位置,又可判断出故障严重程度。但这两种分析在一定程度上都会导致一些有用信息被忽略,不能很好地分析轴承故障的识别过程。与以往研究只提取时域(或频域)特征不同,研究考虑振动信号在时域与频域各自表达形式的优势,提取信号的时域与小波包能量组合成SVM的输入特征向量,使表征振动信号的特征向量具有较好的可靠性和敏感性。
1.1 时域特征提取能够用于表征故障特征的参数有限,在选取时应遵循高敏感性、高可靠性、可实现型的原则。由于轴承振动信号为非周期随机信号,无法表达成具体的数学模型,但在大量重复试验时会出现某种统计规律,得到其重要特征。鉴于有量纲的时域统计特征参数对负载大小和转速较为敏感,且依赖历史数据,选用能灵敏感知轴承缺陷的5个无量纲参数作为时域特征元素,分别为峭度因子、裕度因子、峰值因子、脉冲因子、波形因子。它们不受信号绝对水平影响且无需考虑相对标准值。各特征参数表示如下
峭度因子
| $ {K_{\rm{r}}} = \sum\limits_{i = 1}^n {x_i^4} /nx_{{\rm{rms}}}^4\;\;\;\;; $ | (1) |
裕度因子
| $ L = {x_{{\rm{peak}}}}/{x_{\rm{d}}}\;\;\;\;\;\;; $ | (2) |
峰值因子
| $ C = {x_{{\rm{peak}}}}/{x_{{\rm{rms}}}}\;\;\;\;\;; $ | (3) |
脉冲因子
| $ S = {x_{{\rm{rms}}}}/\left| {{x_{\rm{m}}}} \right|\;\;\;\;\;\;; $ | (4) |
波形因子
| $ Q = {x_{{\rm{peak}}}}/\left| {{x_{\rm{m}}}} \right|\;\;\;\;\;\;\;; $ | (5) |
其中:
由于多分辨分析尺度函数按照二进制变化,所以其频率分辨率在高频段较差。小波包分解能将频带多层次划分,从而进一步分解多分辨率及没有细分的高频部分,使频率分辨率得以提高,且能根据被分析信号的特征自适应选择与信号频谱匹配的频段。基于上述优势,利用小波包分析来提取振动信号能量值。
小波包分解与重构算法如下
由{dtj+1, n}求{dtj, 2n}与{dtj, 2n+1},可得小波分解算法如式(6)所示
| $ \left\{ \begin{array}{l} d_t^{j, 2n} = \sum\limits_k {{h_{k-2l}}d_k^{j + 1, n}}, \\ d_t^{j, 2n + 1} = \sum\limits_k {{g_{k-2l}}d_k^{j + 1, n}}, \end{array} \right. $ | (6) |
由{dtj, 2n}与{dtj, 2n+1}求{dtj+1, n},可得小波包重构算法如式(7)所示
| $ d_t^{j + 1, n} = \sum\limits_k {\left( {{h_{l-2k}}d_k^{j, 2n} + {g_{l-2k}}d_k^{j, 2n + 2}} \right)}, $ | (7) |
其中, gk=(-1)kh1-k,属正交关系。
研究采用db4小波包对振动信号采样序列做3层正交小波包分解,得到8个频带。设分解后各频带能量为
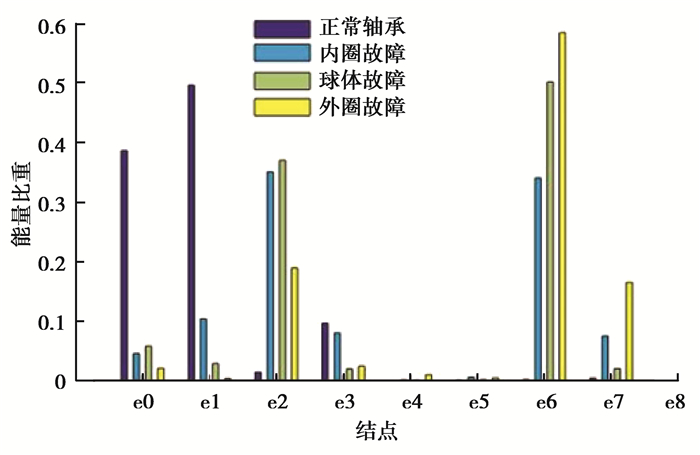
如图 1所示,轴承正常运转时的振动信号能量主要分布在结点0和结点1低频段,而故障发生时,能量集中在结点2和结点6。而不同的故障,能量在这2个频段的的占比是不一样的。
|
图 1 相同严重程度不同故障的能量分布图 Figure 1 Energy distribution for the same severity of different faults |
综合提取的时域特征和小波包能量值,用于轴承故障诊断的特征向量设为T′。为了方便后续数据处理以及使收敛速度加快,对提取的特征进行了归一化处理。则
T′=(Kr, L, C, S, Q, E0, E1, E2, E3, E4, E5, E6, E7)。
2 基于SVM的故障诊断 2.1 SVM理论分析SVM是建立在统计学VC(VC, vapnik-chervonenkis dimension)维理论基础上的一种监督机器学习方法。它通过寻求结构化风险最小来构造最优超平面,提高学习机泛化能力,实现经验风险和置信度的最小化,从而实现在小样本情况下获得良好的分类效果,比传统神经网络方法具有更好的分类能力和计算效率。
因用于轴承故障诊断的训练样本集线性不可分,所以SVM实现分类过程如下:
设有训练样本集A={(xi, yi), i=1, 2…n},其中, xi∈Rd,yi∈{1, -1}为xi所属类别;超平面方程为wx+b,w为权值向量,b为阈值。则能区分样本并使分类间隔最大的优化问题能在约束条件yi(wTw+b)≥1-ζi,ζi≥0下,最小化式(8)
| $ 最小化:\frac{1}{2}\left( {{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}}} \right) + C\sum\limits_{i = 1}^n {{\zeta _i}}, $ | (8) |
其中:C为惩罚系数,由用户指定;ζi为松弛变量。引入拉格朗日乘子法和KKT条件,通过在最优超平面中引用适当的内积核函数K(xi, xj),将线性不可分问题转化为某个高维空间的线性可分问题,避免陷入维数灾难。则最大化问题变为
| $ Q\left( \lambda \right) = \sum\limits_{i = 1}^n {{\lambda _i}}-\frac{1}{2}\sum\limits_{i, j = 1}^l {{\lambda _i}{\lambda _j}{y_i}{y_j}K\left( {{x_i}, {x_j}} \right)。} $ | (9) |
分类函数为
| $ f\left( x \right) = {\rm{sng}}\left( {\sum\limits_{i = 1}^n {{\lambda _i}{y_i}K\left( {{x_i}, x} \right) + b} } \right), $ | (10) |
其中, λ为拉格朗日乘子。研究使用径向基[13](RBF)核函数
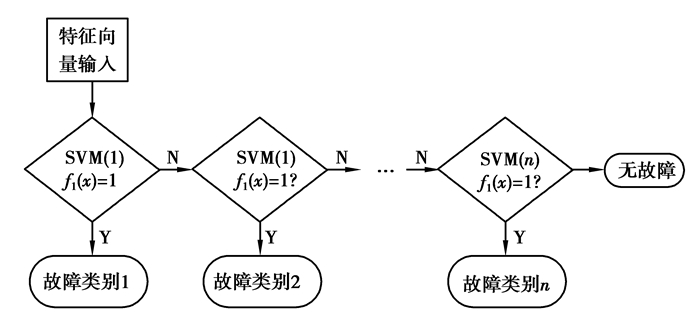
SVM主要是针对二分类提出的,而故障诊断属于多分类问题,所以采用“一对一”的方法来构造多分类器[14]。设有k个类别共l个样本,实现过程是在k个类别中,任意选取2个不同类别的样本构成一个SVM二分类器,则可构造k(k-1)/2个二分类器。当构造类别a分类器时,将属于类别a的训练样本归为一类并标记为正(yia=1),将除去a类别所余下的训练样本作为一类并标记为负(yia=-1)。测试时,将测试样本输入分类器,如果fa(x)=1,则样本为a类别,测试结束。以此类推,则可得到多分类器的分类流程,如图 2所示。
|
图 2 SVM多分类流程图 Figure 2 Flow chart of SVM multi-classification |
故障诊断使用Libsvm3.1[15]工具箱完成,能简单快速有效的实现多类故障的识别。
3 粒子群优化的SVM故障诊断 3.1 粒子群优化算法粒子群优化(PSO)算法源于对鸟类觅食行为的研究,常被用于解决最优解问题,其实现过程为:初始化一群随机粒子,通过迭代找到最优解。在每一次迭代中,粒子通过跟踪2个“极值”来更新自己,一个为粒子本身找到的最优解,称为个体极值;另一个为整个种群找到的最优解,称为全局极值。
设N维目标搜索空间中有m个粒子组成一个群落。将第i个粒子在N维搜索空间中的位置用向量xi=(xi1, xi2, xi3…xiN)表示;“飞翔”速度用向量vi=(vi1, vi2, vi3…viN)表示,i=1, 2…m。粒子速度和位置更新公式如下
| $ \mathit{\boldsymbol{v}}_{{\rm{in}}}^{k + 1} = \mathit{\boldsymbol{\omega v}}_{{\rm{in}}}^k + {c_1}{r_1}\left( {p_{{\rm{in}}}^k-\mathit{\boldsymbol{x}}_{{\rm{in}}}^k} \right) + {c_2}{r_2}\left( {p_{{\rm{gn}}}^k-x_{{\rm{in}}}^k} \right), $ | (11) |
| $ \mathit{\boldsymbol{x}}_{{\rm{in}}}^{k + 1} = \mathit{\boldsymbol{x}}_{{\rm{in}}}^k + \mathit{\boldsymbol{v}}_{{\rm{in}}}^{k + 1}, $ | (12) |
其中:i=1, 2…m;n=1, 2…N;k为迭代次数;c1、c2为学习因子,为非负常数;r1、r2为[0, 1]间的随机数,ω为惯性权值;vin∈[-vmax, vmax],vmax是常数,由使用者设定;pin为第i个粒子搜索到的最优位置;pgn为整个粒子群搜索到的最优位置。迭代终止条件一般选为最大迭代次数或粒子群迄今为止搜索到的最优化位置满足适应阈值。
3.2 PSO算法优化SVM参数由于SVM模型参数直接影响着故障诊断精度,所以对SVM进行参数优化显得尤为重要。而SVM可调参数只有惩罚参数C与核函数参数σ。鉴于PSO算法的寻优效果,研究采用PSO算法来实现SVM模型的参数优化,避免了传统人工试凑确定参数的盲目性。
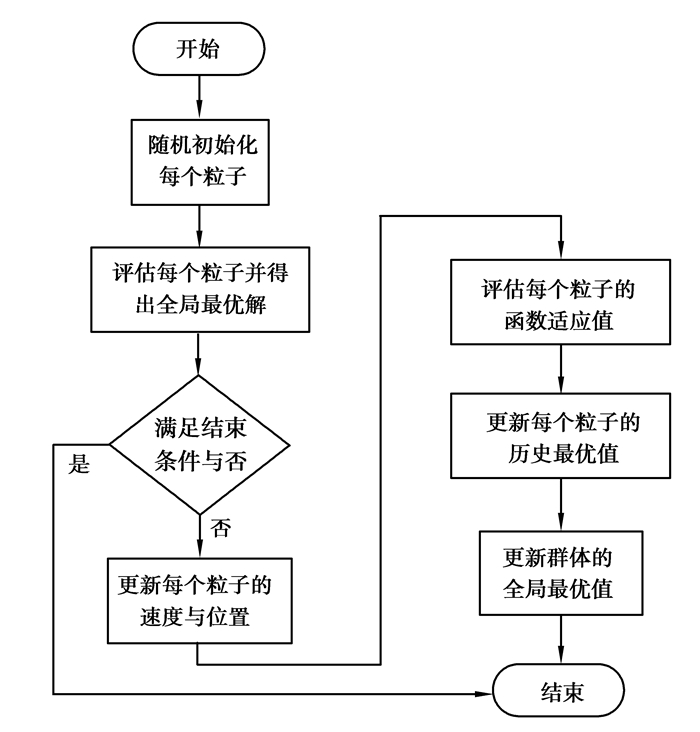
PSO优化SVM参数流程如图 3所示。
|
图 3 PSO优化SVM参数流程图 Figure 3 Flow chart of PSO optimization SVM parameters |
研究用于电机轴承故障诊断的数据集来源于美国凯斯西储大学(case western reserve university)轴承数据中心。数据采集轴承型号为6205-2RS JEM SKF,电机空载且转速为1 797 r/min,使用加速度传感器以12 kHz的频率采集驱动端振动信号。类型包括内圈、外圈及滚珠分别出现故障直径为0.177 8、0.355 6、0.533 4 mm的数据和正常工况下的数据,既样本类别为10,每种工况下的数据采集120组。
研究对传统的基于支持向量机的电机轴承故障诊断方法和采用改进型支持向量机电机轴承故障诊断方法进行对比分析。
4.1 传统SVM的轴承故障诊断方法传统的轴承故障诊断方法仅考虑了电机轴承的外圈、内圈、滚珠3类故障,而没有考虑每类故障的受损程度对故障诊断的影响,因此,传统的诊断方法中,仅采用时域特征或者频域特征,就能够取得理想的诊断结果。
如表 1所示,实验中仅采用了时域特征,不考虑轴承的受损程度,采用故障直径为0.177 8 mm故障数据,故障类型包括内圈、外圈、滚珠故障。因此,总共包括4类样本数据,每一类各包括90组训练样本和30组测试样本。
| 表 1 基于时域特征的SVM故障诊断——不考虑故障严重程度 Table 1 SVM fault diagnosis based on time-domain features——Regardless of the severity of the fault |
实验结果表明,在不考虑轴承受损程度的情况下,仅采用时域特征作为SVM的输入,通过粒子群算法的优化,可以达到100%(120/120)的故障诊断准确率。
然而,在实际的应用中,故障的受损程度是未知的,因此诊断方法中,对每一类轴承故障又进一步的划分为轻微故障、中等故障、严重故障。如表 2所示,分类类型仍然包括正常、内圈故障、外圈故障、滚珠故障。每一种分类的训练样本数量仍然各为90组,测试样本30组,不同的是在每一类故障做了受损程度的划分,而每一类受损程度的样本各包括训练样本30组,测试样本10组。
| 表 2 基于时域特征的SVM故障诊断——考虑故障严重程度 Table 2 SVM fault diagnosis based on time-domain features——Consider the severity of the fault |
实验结果表明,在考虑了故障受损程度的影响后,仅采用时域特征的故障分类准确率仅为81.67%(98/120)。
在同样的实验条件下,考虑故障受损程度,诊断率下降超过18%。因此,在诊断方法中,同时采用了时域与小波包能量特征,使SVM的特征参数有较高的敏感性,提高分类准确率。
4.2 PSO优化SVM参数的故障诊断方法支持向量机的惩罚参数C与RBF核函数参数σ,对分类效果有比较大的影响。因此,寻找合适的参数对支持向量机的分类准确率至关重要。
如表 3所示,将内圈、外圈和滚珠的故障分别划分为3种损伤程度,因此总共包括10个类别,每个类别各包括90组训练样本和30组测试样本。
| 表 3 结合时域与小波包能量特征的PSO-SVM故障诊断 Table 3 PSO-SVM fault diagnosis combining time-domain and wavelet packet energy features |
在粒子群寻优实验中,参数设置:种群数量15,学习因子c1=c2=2,迭代次数100。
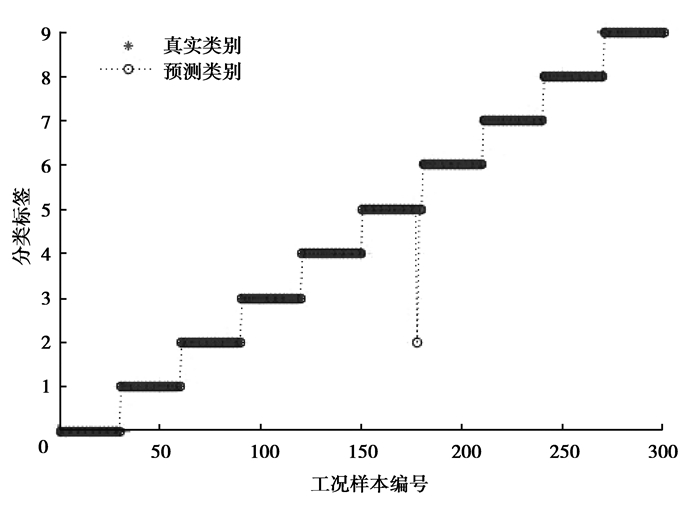
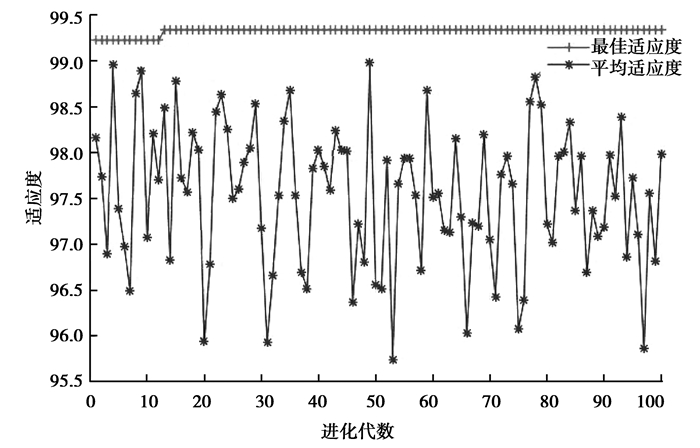
如图 4所示,测试300个样本,分类准确率达到99.67%(299/300), 优于没有优化时的80.33%(241/300)分类准确率。如图 5所示,粒子群参数寻优的平均适应度约为97.5%,最佳适应度达到99.4%,通过寻优获取的惩罚参数C为78.06,RBF核函数参数σ为3.31。
|
图 4 测试结果 Figure 4 Test results |
|
图 5 粒子群适应度曲线 Figure 5 Particle swarm fitness curve |
研究使用了同样的样本,在相同的搜索区域寻优,对比分析了网格搜索算法,遗传算法和粒子群算法在支持向量机惩罚参数C与RBF核函数参数σ中的寻优能力。
由表 4可知,3种算法在优化支持向量机的参数上,其优化效果是比较接近的,但是在用时上(包括特征提取、训练时间与测试时间),粒子群算法优于遗传算法和网格搜索算法。
| 表 4 算法寻优性能对比 Table 4 Comparison of algorithm optimization performance |
研究分别采用了决策树(DT),BP神经网络,深度信念网络(DBN),常规SVM等常用算法,使用相同的数据样本进行训练与测试,随机选择训练与测试样本,并与PSO-SVM算法进行比较,测试准确率取10次平均值。对比结果如表 5所示。决策树用时较少,但故障诊断准确率有待提高;BP神经网络利用特征样本训练,在迭代30次之后的识别率为93.33%,低于PSO-SVM方法。DBN输入为归一化之后的原始数据集,由于网络包括3层隐含层,因此用时较多,但识别率较低,由此可见,深度网络在小样本的情况下并不适用;使用Matlab的默认SVM参数,虽然用时较少,但识别率较低;而在使用粒子群算法优化之后,识别率有了显著提高。
| 表 5 不同分类器的分类指标 Table 5 Classification index of different classifiers |
在轴承故障诊断中,常见的诊断方法都没有考虑不同严重程度的轴承故障对诊断的影响,因此,选取的特征向量尽管维数较低且分类准确率较高,但在实际应用中,分类效果并不理想。
研究从故障诊断的实际应用出发,验证了不同严重程度的轴承故障对分类准确率的影响。在此基础上,分析了振动信号的时域特征与小波包能量特征,使提取的特征在实际诊断中具有较好的可靠性和敏感性。
不仅特征的选取对支持向量机的分类效果有比较大的影响,合适的惩罚参数与RBF核函数参数,也能提高它的分类效果。研究采用粒子群算法对SVM的参数进行寻优,并与网格搜索算法和遗传算法进行了对比。实验结果表明,网格搜索算法、遗传算法及粒子群算法,在基于SVM的轴承故障识别中,对提高识别率都有较好的效果,但在寻优时间上,粒子群算法优于网格搜索算法和遗传算法。
综上所述,提出的轴承故障诊断方法不仅诊断准确率高,而且实用性强。
| [1] | Zhou W, Habetler T G, Harley R G. Bearing fault detection via stator current noise cancellation and statistical control[J]. IEEE Transactions on Industrial Electronics, 2008, 55(12): 4260–4269. DOI:10.1109/TIE.2008.2005018 |
| [2] |
丁瑞成, 黄友锐, 陈珍萍, 等.
LMD和SVM相结合的电机轴承故障诊断研究[J]. 组合机床与自动化加工技术, 2016(8): 81–84.
DING Ruicheng, HUANG Yourui, CHEN Zhenping, et al. Fault diagnosis of motor bearings based on LMD and SVM[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(8): 81–84. (in Chinese) |
| [3] | Bu Y, Wu J, Ma J, et al. The rolling bearing fault diagnosis based on LMD and LS-SVM[C]//Chinese Control and Decision Conference. Changsha, China: IEEE, 2014: 3797-3801. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-KZJC201405001717.htm |
| [4] | Saidi L, Ben Ali J, Fnaiech F, et al. Bi-spectrum based-EMD applied to the non-stationary vibration signals for bearing faults diagnosis[C]//Soft Computing and Pattern Recognition. Tunisia: IEEE, 2014: 25-30. http://europepmc.org/abstract/med/24975564 |
| [5] | Zhang X, Liang Y, Zhou J, et al. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM[J]. Measurement, 2015, 69(6): 164–179. |
| [6] | Li C, Zong X, Gudake M. A survey of online fault diagnosis for pv module based on BP neural network[C]//International Conference on Smart City and Systems Engineering. Dalian, China: IEEE Computer Society, 2016: 483-486. http://doi.ieeecomputersociety.org/10.1109/ICSCSE.2016.0132 |
| [7] | Muralidharan V, Sugumaran V. Feature extraction using wavelets and classification through decision tree algorithm for fault diagnosis of mono-block centrifugal pump[J]. Measurement, 2013, 46(1): 353–359. DOI:10.1016/j.measurement.2012.07.007 |
| [8] | Rajeswari C, Sathiyabhama B, Devendiran S, et al. Bearing fault diagnosis using wavelet packet transform, Hybrid PSO and support vector machine[J]. Procedia Engineering, 2014, 97(12): 1772–1783. |
| [9] | Vapnik V N. The nature of statistical learning theory[J]. Neural Networks IEEE Transactions on, 1995, 10(5): 988–999. |
| [10] | Zhang X L, Chen W, Wang B J, et al. Intelligent fault diagnosis of rotating machinery using support vector machine with ant colony algorithm for synchronous feature selection and parameter optimization[J]. Neurocomputing, 2015, 167: 260–279. DOI:10.1016/j.neucom.2015.04.069 |
| [11] | Chen F, Tang B, Chen R, et al. A novel fault diagnosis model for gearbox based on wavelet support vector machine with immune genetic algorithm[J]. Measurement, 2013, 46(1): 220–232. DOI:10.1016/j.measurement.2012.06.009 |
| [12] | Kennedy J, Eberhart R. Particle swarm optimization[C]//IEEE International Conference on Neural Networks, 1995. Tunisia: IEEE, 1995: 1942-1948. |
| [13] |
周绍磊, 廖剑, 史贤俊.
RBF-SVM的核参数选择方法及其在故障诊断中的应用[J]. 电子测量与仪器学报, 2014, 28(3): 240–246.
ZHOU Shaolei, LIAO Jian, SHI Xianjun. Selection of nuclear parameters for RBF-SVM and its application in fault diagnosis[J]. Journal of Electronic Measurement and Instrumentation, 2014, 28(3): 240–246. (in Chinese) |
| [14] |
许允之, 方磊, 张建文, 等.
基于最小二乘支持向量机的电机故障鉴别[J]. 电力系统保护与控制, 2012, 40(14): 63–68.
XU Yunzhi, FANG Lei, ZHANG Jianwen, et al. Motor fault identification based on least squares support vector machine[J]. Power System Protection and Control, 2012, 40(14): 63–68. DOI:10.7667/j.issn.1674-3415.2012.14.011 (in Chinese) |
| [15] | Chang C C, Lin C J. Libsvm:A library for support vector machines[J]. Acm Transactions on Intelligent Systems & Technology, 2007, 2(3): 389–396. |
 2018, Vol. 41
2018, Vol. 41

