2. 重庆大学 汽车工程学院, 重庆 400044
2. School of Automotive Engineering, Chongqing University, Chongqing, 400044, P. R. China
复杂结构刚体的惯性参数识别是对其进行动力学分析和控制的前提和关键[1-2]。目前刚体惯性参数辨识方法主要有时域法和频域法[3],时域法分为落体测试法和扭摆测试法[4-6]。落体测试法不能辨识复杂刚体结构的惯性参数[7],扭摆测试法在测试过程中需要改变刚体姿态至少6次,对于大型复杂结构刚体,操作过程复杂,识别精度与效率低。Tang等[6]提出一种改进的三线摆试验装置,无须调整刚体位姿即可实现质心与旋转轴线重合,缩短了三线摆法的测试周期,但一次装夹只能识别一个惯性参数。王秋晓等[8]将质心台和扭摆台合并为一质量特性参数综合试验台,可实现一次装夹下识别刚体的10个惯性参数,但试验操作过程烦琐,试验台结构复杂,造价较高。
频域法[9-15]能够解决时域法不可避免的问题,因此得到了国内外相关研究人员的广泛关注。Malekjafarian等[11]利用正则振型的正交性识别刚体的10个惯性参数,但其惯性参数识别误差达到了40%。Xu等[12]用弹性绳将发动机悬吊起来,对发动机本身进行激振测试,但由于发动机外形结构很复杂,导致分布在发动机表面的激励点和响应点坐标测量误差增大,同时激励方向、传感器测量轴与基准轴存在一定夹角,使得发动机惯性参数识别精度不高。Huang等[14]利用直接系统识别法将系统刚度矩阵和阻尼矩阵从方程中分离出来,减少了未知量,但该方法的可靠性与识别精度不得而知。
针对上述问题,笔者在频响函数质量线法识别刚体惯性参数的基础上,提出了一种惯性参数识别装置。将待测刚体固定于该装置的托盘上,对托盘进行频率响应测试,利用频响函数质量线法,实现刚体惯性参数的精确与高效识别。
1 刚体惯性参数识别方法待测刚体固定于托盘上,在微小振动下刚体与托盘没有相对位移,忽略弹簧刚度和阻尼的影响,则振动模型可简化为如图 1所示的六自由度模型。

|
图 1 刚体与托盘六自由度振动模型 Figure 1 Six DOF vibration model of rigid body and pallet |
在Ej点激励下刚体和托盘的运动方程可表示为
| $ \left\{ \begin{array}{l} {F_x} = m{{\ddot x}_{{\rm{o}}{{\rm{e}}_j}}} + mz\ddot \beta - my\ddot \gamma ,\\ {F_y} = m{{\ddot y}_{{\rm{o}}{{\rm{e}}_j}}} - mz\ddot \alpha + mx\ddot \gamma ,\\ {F_z} = m{{\ddot z}_{{\rm{o}}{{\rm{e}}_j}}} + my\ddot \alpha - mx\ddot \beta ,\\ {M_x} = - mz{{\ddot y}_{{\rm{o}}{{\rm{e}}_j}}} + my{{\ddot z}_{{\rm{o}}{{\rm{e}}_j}}} + {I_{xx}}\ddot \alpha - {I_{xy}}\beta - {I_{xz}}\ddot \gamma ,\\ {M_y} = mz{{\ddot x}_{{\rm{o}}{{\rm{e}}_j}}} - mx{{\ddot z}_{{\rm{o}}{{\rm{e}}_j}}} - {I_{xy}}\ddot \alpha + {I_{yy}}\ddot \beta - {I_{yz}}\ddot \gamma ,\\ {M_z} = - my{{\ddot x}_{{\rm{o}}{{\rm{e}}_j}}} + mx{{\ddot y}_{{\rm{o}}{{\rm{e}}_j}}} - {I_{xz}}\ddot \alpha - {I_{yz}}\ddot \beta + {I_{zz}}\ddot \gamma 。\end{array} \right. $ | (1) |
式中:m为待测刚体与托盘总质量;xc,yc,zc为其质心坐标;Ixx,Iyy,Izz为其转动惯量;Ixy,Ixz,Iyz为其惯性积;
将式(1)写成矩阵形式
| $ \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{a}}_{{\rm{o}}{{\rm{e}}_j}}} = {\mathit{\boldsymbol{F}}_j}, $ | (2) |
式中:M为质量矩阵,是对称矩阵;aoej为原点处加速度响应矩阵;Fj为原点处激励力向量。
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} m&0&0&0&{mz}&{ - my}\\ 0&m&0&{ - mz}&0&{mx}\\ 0&0&m&{my}&{ - mx}&0\\ 0&{ - mz}&{my}&{{I_{xx}}}&{ - {I_{xy}}}&{ - {I_{zx}}}\\ {mz}&0&{ - mx}&{ - {I_{xy}}}&{{I_{yy}}}&{ - {I_{yz}}}\\ { - my}&{mx}&0&{ - {I_{xz}}}&{ - {I_{yz}}}&{{I_{zz}}} \end{array}} \right], $ | (3) |
| $ {\mathit{\boldsymbol{a}}_{{\rm{o}}{{\rm{e}}_j}}} = {\left\{ {\begin{array}{*{20}{c}} {{{\ddot x}_{{\rm{o}}{{\rm{e}}_j}}}}&{{{\ddot y}_{{\rm{o}}{{\rm{e}}_j}}}}&{{{\ddot z}_{{\rm{o}}{{\rm{e}}_j}}}}&{\ddot \alpha }&{\ddot \beta }&{\ddot \gamma } \end{array}} \right\}^{\rm{T}}}。$ | (4) |
| $ {\mathit{\boldsymbol{F}}_j} = {\left\{ {\begin{array}{*{20}{c}} {{F_x}}&{{F_y}}&{{F_z}}&{{M_x}}&{{M_y}}&{{M_z}} \end{array}} \right\}^{\rm{T}}}。$ | (5) |
假设在Ej点激励,Pi点加速度响应与原点加速度响应的关系为
| $ \left\{ {\begin{array}{*{20}{c}} {{{\ddot x}_{{{\rm{p}}_i}{{\rm{e}}_j}}}}\\ {{{\ddot y}_{{{\rm{p}}_i}{{\rm{e}}_j}}}}\\ {{{\ddot z}_{{{\rm{p}}_i}{{\rm{e}}_j}}}}\\ \vdots \\ {{{\ddot x}_{{{\rm{p}}_n}{{\rm{e}}_j}}}}\\ {{{\ddot y}_{{{\rm{p}}_n}{{\rm{e}}_j}}}}\\ {{{\ddot z}_{{{\rm{p}}_n}{{\rm{e}}_j}}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&{{z_{{{\rm{p}}_1}}}}&{ - {y_{{{\rm{p}}_1}}}}\\ 0&1&0&{ - {z_{{{\rm{p}}_1}}}}&0&{{x_{{{\rm{p}}_1}}}}\\ 0&0&1&{{y_{{{\rm{p}}_1}}}}&{ - {x_{{{\rm{p}}_1}}}}&0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ 1&0&0&0&{{z_{{{\rm{p}}_n}}}}&{ - {y_{{{\rm{p}}_n}}}}\\ 0&1&0&{ - {z_{{{\rm{p}}_n}}}}&0&{{x_{{{\rm{p}}_n}}}}\\ 0&0&1&{{y_{{{\rm{p}}_n}}}}&{ - {x_{{{\rm{p}}_n}}}}&0 \end{array}} \right] \cdot \left\{ {\begin{array}{*{20}{c}} {{{\ddot x}_{{\rm{o}}{{\rm{e}}_j}}}}\\ {{{\ddot y}_{{\rm{o}}{{\rm{e}}_j}}}}\\ {{{\ddot z}_{{\rm{o}}{{\rm{e}}_j}}}}\\ {{{\ddot \alpha }_j}}\\ {{{\ddot \beta }_j}}\\ {{{\ddot \gamma }_j}} \end{array}} \right\}, $ | (6) |
式中:
将式(6)写成
| $ {\mathit{\boldsymbol{a}}_{{\rm{p}}{{\rm{e}}_j}}} = {\mathit{\boldsymbol{T}}_{\rm{p}}}{\mathit{\boldsymbol{a}}_{{\rm{o}}{{\rm{e}}_j}}}, $ | (7) |
式中:apej为测点加速度响应矩阵;Tp为响应点坐标变换矩阵。
当rank(Tp)≥6时,式(7)可写成
| $ {\mathit{\boldsymbol{a}}_{{\rm{o}}{{\rm{e}}_j}}} = {\left( {{\mathit{\boldsymbol{T}}_{\rm{p}}}^{\rm{T}}{\mathit{\boldsymbol{T}}_{\rm{p}}}} \right)^{ - 1}}{\mathit{\boldsymbol{T}}_{\rm{p}}}^{\rm{T}}{\mathit{\boldsymbol{a}}_{{\rm{p}}{{\rm{e}}_j}}}。$ | (8) |
假设对Ej点的激励力大小为fj,激励力方向与坐标轴夹角分别为
| $ {\mathit{\boldsymbol{F}}_j} = \mathit{\boldsymbol{T}}_j^{\rm{T}}\mathit{\boldsymbol{\theta }}_j^{\rm{T}}{f_j}, $ | (9) |
式中:矩阵Tj为激励点坐标变换矩阵;θj为激励力方向余弦矩阵,即
| $ {\mathit{\boldsymbol{T}}_j} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&{{z_j}}&{ - {y_j}}\\ 0&1&0&{ - {z_j}}&0&{{x_j}}\\ 0&0&1&{{y_j}}&{ - {x_j}}&0 \end{array}} \right], $ | (10) |
| $ {\mathit{\boldsymbol{\theta }}_j} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _{{x_j}}}}&{\cos {\theta _{{y_j}}}}&{\cos {\theta _{{z_j}}}} \end{array}} \right]。$ | (11) |
则当有m个激励点时,式(9)可写成矩阵形式有
| $ \mathit{\boldsymbol{F}} = {\mathit{\boldsymbol{T}}_{\rm{e}}}\mathit{\boldsymbol{f}}, $ | (12) |
式中:
| $ \mathit{\boldsymbol{F}} = \left[ {{\mathit{\boldsymbol{F}}_1},{\mathit{\boldsymbol{F}}_2}, \cdots ,{\mathit{\boldsymbol{F}}_m}} \right], $ |
| $ {\mathit{\boldsymbol{T}}_{\rm{e}}} = \left[ {\mathit{\boldsymbol{T}}_1^{\rm{T}}\mathit{\boldsymbol{\theta }}_1^{\rm{T}},\mathit{\boldsymbol{T}}_2^{\rm{T}}\mathit{\boldsymbol{\theta }}_2^{\rm{T}}, \cdots ,\mathit{\boldsymbol{T}}_m^{\rm{T}}\mathit{\boldsymbol{\theta }}_m^{\rm{T}}} \right], $ |
| $ \mathit{\boldsymbol{f}} = {\rm{diag}}\left( {{f_1},{f_2}, \cdots ,{f_m}} \right)。$ |
则m个激励点、n个响应点下系统的振动运动方程为
| $ \mathit{\boldsymbol{M}}{\left( {\mathit{\boldsymbol{T}}_{\rm{p}}^{\rm{T}}{\mathit{\boldsymbol{T}}_{\rm{p}}}} \right)^{ - 1}}\mathit{\boldsymbol{T}}_{\rm{p}}^{\rm{T}}{\mathit{\boldsymbol{a}}_{{\rm{pe}}}} = \mathit{\boldsymbol{T}}_{\rm{e}}^{\rm{T}}\mathit{\boldsymbol{f}}。$ | (13) |
式(13)两边同时乘以f-1可得
| $ \mathit{\boldsymbol{M}}{\left( {\mathit{\boldsymbol{T}}_{\rm{p}}^{\rm{T}}{\mathit{\boldsymbol{T}}_{\rm{p}}}} \right)^{ - 1}}\mathit{\boldsymbol{T}}_{\rm{p}}^{\rm{T}}\mathit{\boldsymbol{H}} = \mathit{\boldsymbol{T}}_{\rm{e}}^{\rm{T}}, $ | (14) |
式中H为m个激励点、n个响应点的频响函数矩阵,取每条频响函数曲线的实部可得。
令
| $ \mathit{\boldsymbol{M\xi }} = \mathit{\boldsymbol{T}}_{\rm{e}}^{\rm{T}}, $ | (15) |
式中只有质量矩阵M未知。由最小二乘法可得
| $ \mathit{\boldsymbol{M}} = \mathit{\boldsymbol{T}}_{\rm{e}}^{\rm{T}}{\mathit{\boldsymbol{\xi }}^{\rm{T}}}{\left( {\mathit{\boldsymbol{\xi }}{\mathit{\boldsymbol{\xi }}^{\rm{T}}}} \right)^{ - 1}}。$ | (16) |
当求得质量矩阵M后,则可根据式(3)求得待测刚体与托盘的惯性参数之和
| $ \mathit{\boldsymbol{I}} = \left\{ {\begin{array}{*{20}{c}} m&x&y&z&{{I_{xx}}}&{{I_{yy}}}&{{I_{zz}}}&{{I_{xy}}}&{{I_{xz}}}&{{I_{yz}}} \end{array}} \right\}。$ |
由于托盘惯性参数Ia已知,
| $ {\mathit{\boldsymbol{I}}_{\rm{a}}} = \left\{ {\begin{array}{*{20}{c}} {{m_{\rm{a}}}}&{{x_{\rm{a}}}}&{{y_{\rm{a}}}}&{{z_{\rm{a}}}}&{{{\left( {{I_{xx}}} \right)}_{\rm{a}}}}&{{{\left( {{I_{yy}}} \right)}_{\rm{a}}}}&{{{\left( {{I_{zz}}} \right)}_{\rm{a}}}}&{{{\left( {{I_{xy}}} \right)}_{\rm{a}}}}&{{{\left( {{I_{xz}}} \right)}_{\rm{a}}}}&{{{\left( {{I_{yz}}} \right)}_{\rm{a}}}} \end{array}} \right\}。$ |
用式(17)可计算得到待测刚体所有惯性参数Ib。
| $ \left\{ \begin{array}{l} {m_{\rm{b}}} = m - {m_{\rm{a}}},\\ {x_{\rm{b}}} = \frac{1}{{{m_{\rm{b}}}}}\left( {mx - {m_{\rm{a}}}{x_{\rm{a}}}} \right),\\ {y_{\rm{b}}} = \frac{1}{{{m_{\rm{b}}}}}\left( {my - {m_{\rm{a}}}{y_{\rm{a}}}} \right),\\ {z_{\rm{b}}} = \frac{1}{{{m_{\rm{b}}}}}\left( {mz - {m_{\rm{a}}}{z_{\rm{a}}}} \right),\\ {\left( {{I_{{\rm{cd}}}}} \right)_{\rm{b}}} = {I_{{\rm{cd}}}} - {\left( {{I_{{\rm{cd}}}}} \right)_{\rm{a}}}。\end{array} \right. $ | (17) |
式中:c, d分别代表x, y, z。
2 惯性参数识别试验装置仿真分析 2.1 惯性参数识别试验装置惯性参数识别装置由托盘和支架构成,托盘通过6根弹簧与支架连接,用于承载和固定待测刚体。在Adams动力学软件中建立仿真模型,如图 2所示。由于激励点和响应点作用于托盘上的精加工平面,因此激励点坐标、响应点坐标以及激励角度的误差可以控制在很小的范围内,从而提高刚体惯性参数识别精度,同时降低了测试难度,减少了测试时间。

|
图 2 多体动力学模型 Figure 2 Multi-body dynamic model |
模型主要结构参数如表 1所示。仿真采用9点激励,4点响应,激励点和响应点分布在托盘边缘。激励采用正弦扫频信号,设置好各仿真参数后进行仿真,然后将仿真数据导入识别程序进行惯性参数识别。待测刚体惯性参数识别仿真结果为:10个惯性参数中最大误差只有0.028%,仿真识别值及其误差如表 2所示。
| 表 1 模型参数 Table 1 Model parameters |
| 表 2 惯性参数试验识别结果 Table 2 Inertia parameter identification result |
本文惯性参数识别方法忽略了悬置弹簧的刚度和阻尼的影响,为了验证识别方法的正确性,需分析弹簧刚度与弹簧阻尼的变化对惯性参数识别精度的影响规律。图 3与图 4分别为单根弹簧刚度和单根弹簧阻尼与惯性参数识别误差的关系,由图可知,所有惯性参数识别误差随弹簧刚度与阻尼的增大而增大,为了减小二者对惯性参数识别误差的影响,在满足支撑条件下,待测刚体支撑系统刚度和阻尼都应尽可能小。

|
图 3 弹簧刚度对识别精度的影响 Figure 3 Influence of stiffness on identification precision |

|
图 4 弹簧阻尼对识别精度的影响 Figure 4 Influence of damping on identification precision |
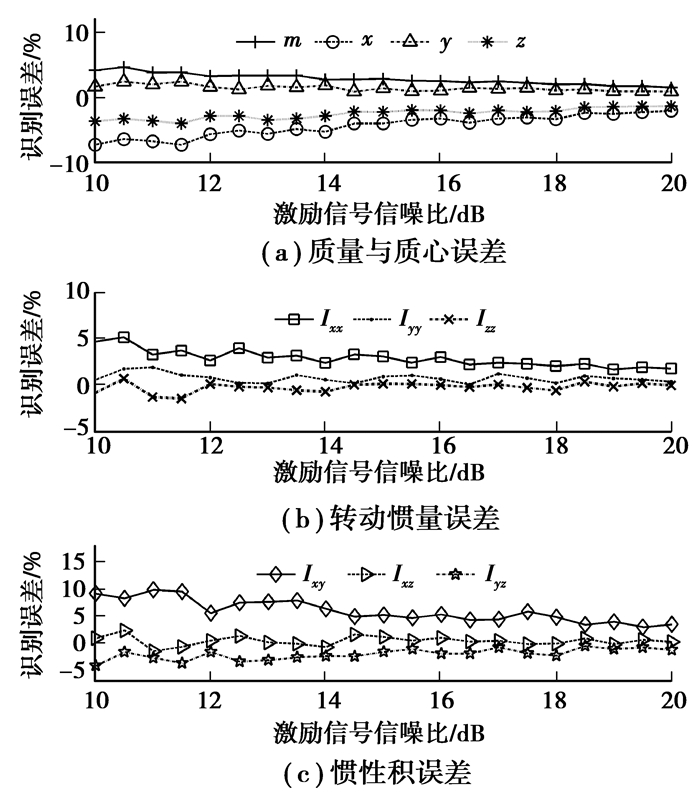
频率响应函数测量过程中,无论是激励端还是响应端都会存在噪声,噪声的存在会影响惯性参数识别精度。在激励信号中分别加入一定信噪比的白噪声,惯性参数识别误差与激励噪声的关系如图 5所示。随着激励信噪比的增加,惯性参数识别误差减小。在实际试验时,通过多次激振试验发现,激励噪声信噪比在19 dB左右,由仿真识别结果可知,信噪比为19 dB的噪声引起的惯性参数识别误差在5%以内。
|
图 5 噪声对识别精度的影响 Figure 5 Influence of noise on identification precision |
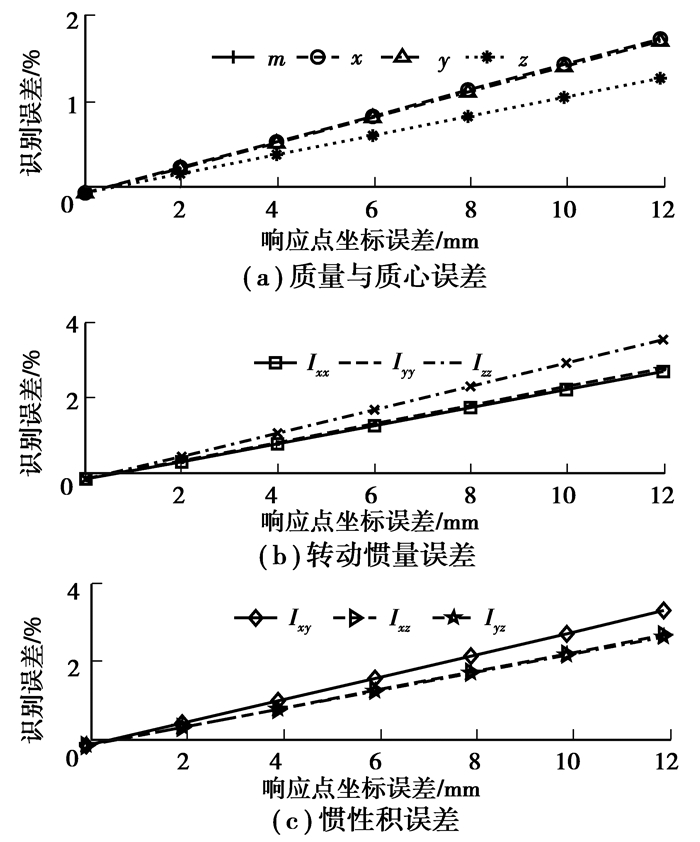
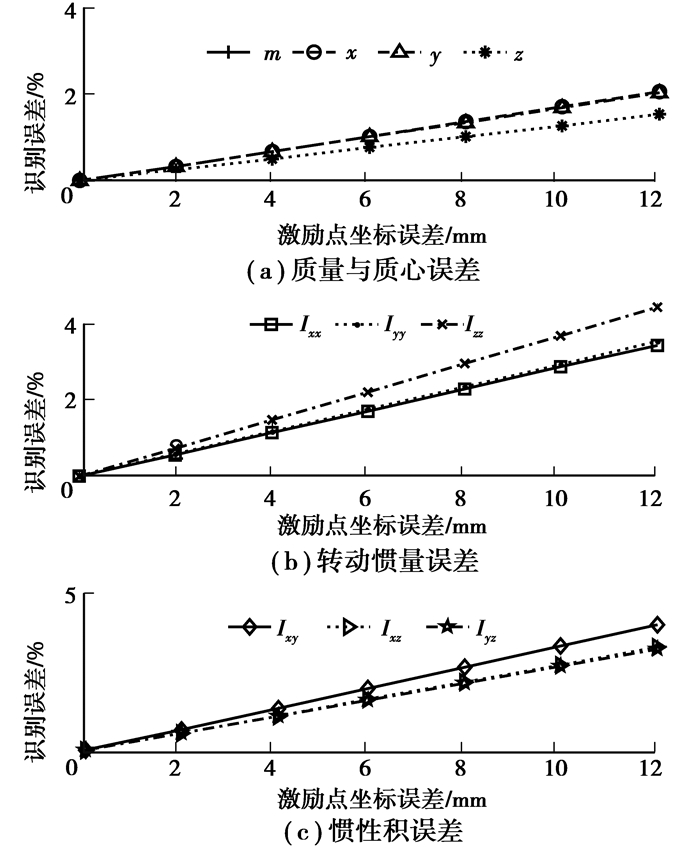
激励点坐标构成式(14)中Te矩阵,响应点坐标构成式(14)中Tp矩阵,由于实验中力锤作用点坐标、加速度传感器贴合点坐标总会存在一定的测量误差,计算时,分别给每个激励点和响应点坐标加入0,2,…,12 mm的误差,其结果分别如图 6和图 7所示。由图可知,随着激励点、响应点坐标误差增大,质量识别误差没有变化,其余惯性参数识别误差增大,当坐标误差不超过12 mm时,所有惯性参数识别误差在5%以内。
|
图 6 响应点坐标误差对识别精度的影响 Figure 6 Influence of response point coordinate error on identification precision |
|
图 7 激励点坐标误差对识别精度的影响 Figure 7 Influence of excitation point coordinate error on identification precision |
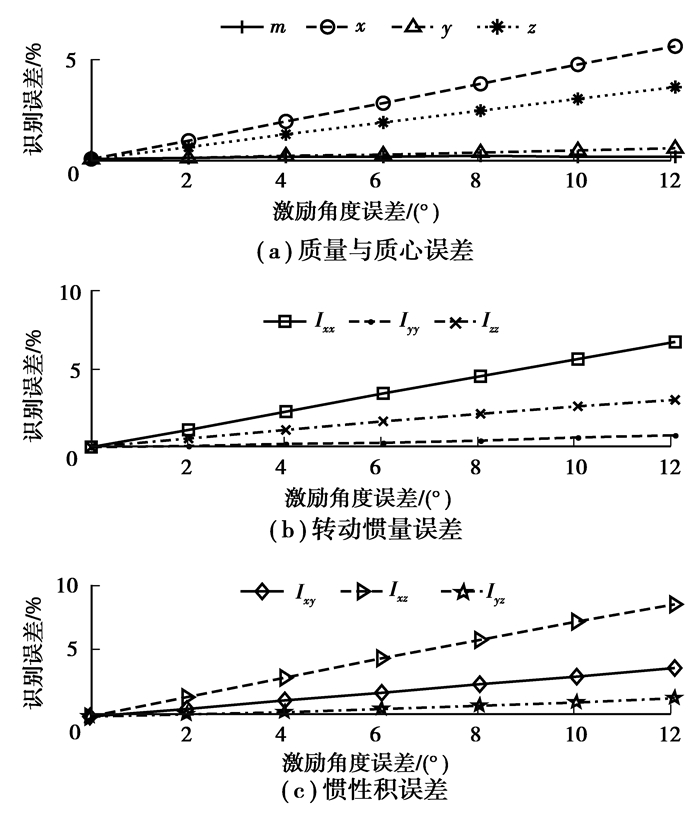
激励角度与传感器安装角度分别影响Te矩阵和Tp矩阵,由于测试中采用力锤敲击的方式,传感器亦为手动贴合,二者必然会存在误差。分别给每个激励角度与传感器安装角度加入0°,2°,…,12°的误差,其结果分别如图 8、图 9所示。
|
图 8 激励角度误差对识别精度的影响 Figure 8 Influence of Excitation angle error on identification precision |
|
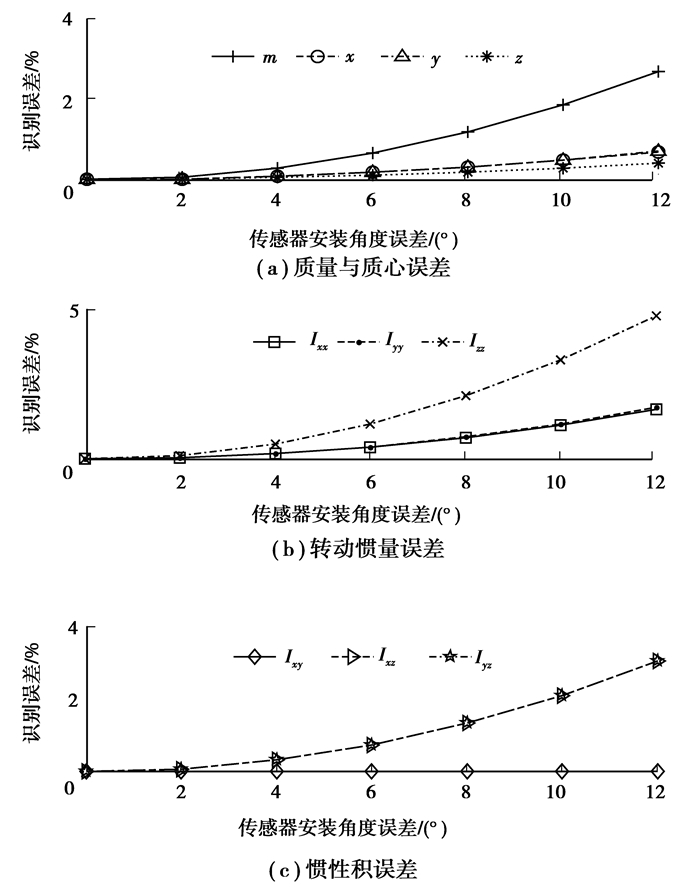
图 9 传感器安装角度误差对识别精度的影响 Figure 9 Influence of sensor installation angle error on identification precision |
由图 8、图 9可知,所有惯性参数误差都随激励角度误差和传感器安装角度误差的增大而增大。由图 9可知,传感器安装角度误差不超过12°时,所有惯性参数识别误差在5%以内。由图 8(c)可知,当激励角度误差为8°时,惯性积Ixz的误差达到了6%,表明激励角度误差的影响较大。
3 惯性参数试验识别 3.1 试验按照2.1所述搭建试验台,其中每根拉伸弹簧在其弹性主轴方向的刚度为1 000±5 N/m,阻尼很小,可忽略不计。
式(16)采用最小二乘法,需满足条件rank(H)≥6,则激励点数应大于等于6。由于矩阵条件数的影响,响应点数应大于等于3[12]。激励方向的选取原则为所有激励方向的延长线不能交于一点,不能通过质心。本次试验一共测试了12个激励点和6个响应点,并选取其中相干性最好的9个激励点和4个响应点进行惯性参数识别。
待测刚体为一个表面平整光滑的长方体钢块,长为210 mm,宽为100 mm,高为160 mm,中部有直径为80 mm的通孔。将其固定于托盘上,力锤敲击托盘上的激励点,三向加速度传感器拾取托盘表面振动加速度信号,输入到多通道分析仪,得到加速度频响函数。试验及其设备如图 10所示。

|
图 10 惯性参数识别试验 Figure 10 Experiment of inertia parameter identification |
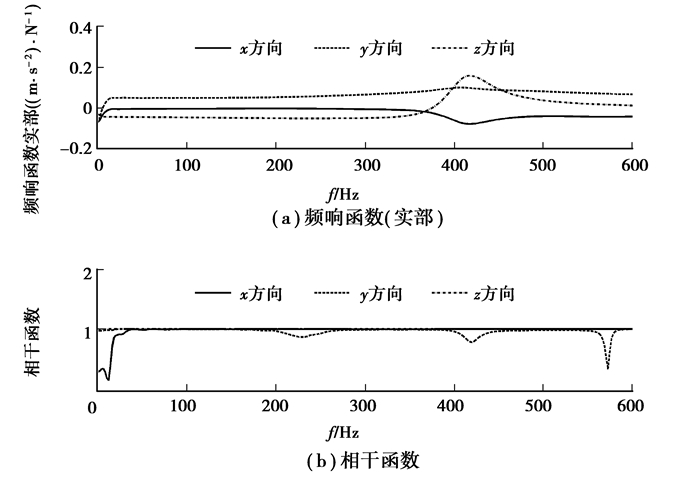
试验测得所有激励点响应点的加速度频响函数,由于数据太多,只选取1个激励点1个响应点的数据作为说明,加速度频响函数如图 11(a)所示,相干函数如图 11(b)所示。选取80~120 Hz作为计算频带,与第一阶弹性体模态(418 Hz)相隔较远且计算频带内的频响函数质量线足够平滑。由图 11(b)可知在所选计算频带相干函数接近于1,说明数据可靠。
|
图 11 频响函数与相干函数 Figure 11 Frequency response function and coherence function |
为了减小噪声等因素的影响,在计算频带内选取10组不同频率下的数据进行平均,再用平均后的数据导入笔者编译的惯性参数识别程序进行计算。惯性参数试验识别结果如表 2所示。由表可知,质量识别误差最小,质心误差转动惯量次之,惯性积误差最大,但所有惯性参数误差都在5%以内。由此可见,试验识别误差大于仿真识别误差,这是因为仿真识别为理想状态,仅存在计算时的舍入误差,而试验识别时2.2.2至2.2.4所述影响因素不可避免地同时存在,增大了识别误差。
4 结论基于频率响应函数质量线的惯性参数识别方法,设计了一种复杂结构刚体惯性参数识别装置,通过仿真与试验分析,得到以下结论:
1) 在满足支撑条件下,系统刚度和阻尼应尽可能小;激励噪声、激励点坐标误差、响应点坐标误差、激励
角度误差与传感器安装角度误差对惯性参数识别精度均有不同程度的影响,其中激励角度误差的影响最为严重。
2) 试验结果表明样件的最大惯性参数识别误差为4.7%,满足工程应用要求,验证了基于质量线法惯性参数识别试验装置的准确性。
3) 笔者基于质量线法的惯性参数识别装置适用于识别一切具有刚体特性物体的惯性参数,不受对象外形及结构限制,识别过程简单,识别精度高,为刚体动力学分析,优化设计等提供理论参考。
| [1] |
Sharifi G, Zabihian E. An effective approach to identify the mass properties of a satellite attitude dynamics simulator[J]. Australian Journal of Mechanical Engineering, 2018(8): 1-10. |
| [2] |
尚会超, 张力, 陈江, 等. 摩托车法规行驶循环的发动机台架模拟[J]. 重庆大学学报, 2013, 36(3): 6-12. SHANG Huichao, ZHANG Li, CHEN Jiang, et al. Simulation of regulatory driving cycle for motorcycle on the engine test bench[J]. Journal of Chongqing University, 2013, 36(3): 6-12. (in Chinese) |
| [3] |
Ashory M R, Malekjafarian A, Harandi P. On the accuracy of estimation of rigid body inertia properties from modal testing results[J]. Structural Engineer and Mechanics, 2010, 35(1): 53-65. DOI:10.12989/sem.2010.35.1.053 |
| [4] |
Hou Z, Lu Y, Lao Y, et al. A new trifilar pendulum approach to identify all inertia parameters of a rigid body or assembly[J]. Mechanism and Machine Theory, 2009, 44(6): 1270-1280. DOI:10.1016/j.mechmachtheory.2008.07.004 |
| [5] |
Ringegni P L, Actis M D, Patanella A J. An experimental technique for determining mass inertial properties of irregular shape bodies and mechanical assemblies[J]. Measurement, 2001, 29(1): 63-75. DOI:10.1016/S0263-2241(00)00028-2 |
| [6] |
Tang L, Shangguan W B. An improved pendulum method for the determination of the center of gravity and inertia tensor for irregular-shaped bodies[J]. Measurement, 2011, 44(10): 1849-1859. DOI:10.1016/j.measurement.2011.09.004 |
| [7] |
王海林, 司嵘嵘, 李相银. 落体法测量刚体转动惯量实验中引起测量值偏离的因素分析[J]. 物理实验, 2012, 32(5): 25-27. WANG Hailin, SI Rongrong, LI Xiangyin. Error analysis in measurement of rigid body rotational inertia by falling body method[J]. Physics Experimentation, 2012, 32(5): 25-27. (in Chinese) |
| [8] |
王秋晓, 王迎. 飞行器质量特性参数测量[J]. 重庆大学学报, 2011, 34(12): 23-28. WANG Qiuxiao, WANG Ying. A new measurement method for mass property parameters[J]. Journal of Chongqing University, 2011, 34(12): 23-28. (in Chinese) DOI:10.11835/j.issn.1000-582X.2011.12.004 |
| [9] |
郭峰, 吕振华, 侯之超. 动力总成刚体惯性参数的识别方法研究[J]. 汽车技术, 2004(8): 15-19. GUO Feng, LYU Zhenhua, HOU Zhichao. Study on identification method of inertia parameters of powertrain rigid body[J]. Automobile Technology, 2004(8): 15-19. (in Chinese) DOI:10.3969/j.issn.1000-3703.2004.08.005 |
| [10] |
金新灿, 孙守光, 陈光雄. 基于试验频响函数刚体特性参数的计算及其应用[J]. 机械工程学报, 2005, 41(3): 206-210. JIN Xincan, SUN Shouguang, CHEN Guangxiong. Calculation and applications of rigid body properties based on experimental frequency response function data[J]. Chinese Journal of Mechanical Engineering, 2005, 41(3): 206-210. (in Chinese) DOI:10.3321/j.issn:0577-6686.2005.03.039 |
| [11] |
Malekjafarian A, Ashory M R, Khatibi M M, et al. Rigid body stiffness matrix for identification of inertia properties from output-only data[J]. European Journal of Mechanics A-Solids, 2016, 59: 85-94. DOI:10.1016/j.euromechsol.2016.03.009 |
| [12] |
Xu C, Ding K, Yang Z. Identification of engine inertia parameters on the basis of frequency response functions[J]. Vehicle Design, 2012, 60(1/2): 121-137. DOI:10.1504/IJVD.2012.049161 |
| [13] |
Mucchi E, Fiorati S, Di Gregorio R, et al. Determining the rigid-body inertia properties of cumbersome systems:Comparison of techniques in time and frequency domain[J]. Experimental Techniques, 2011, 35(3): 36-43. DOI:10.1111/ext.2011.35.issue-3 |
| [14] |
Huang S J, Lallement G. Direct estimation of rigid body properties from harmonic forced responses[C]//Proceedings of the International Modal Analysis Conference-IMAC. Orlando, FL, USA: SEM, Bethel, CT, United States, 1997: 175-180.
|
| [15] |
Lee H, Lee Y B, Park Y S. Response and excitation points selection for accurate rigid-body inertia properties identification[J]. Mechanical Systems and Signal Processing, 1999, 13(4): 571-592. DOI:10.1006/mssp.1998.0190 |
 2018, Vol. 41
2018, Vol. 41


