2. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044;
3. 国网电力科学研究院武汉南瑞有限公司, 武汉 430074
2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, School of Electrical Engineering, Chongqing University, Chongqing 400044, P. R. China;
3. Wuhan Nari Limited Company, State Grid Electric Power Research Institute, Wuhan 430074, P. R. China
随着电网规模越来越大,断路器的开断能力与系统短路电流间的矛盾日益突出。现有330 kV及以上电压等级的断路器主要为SF6断路器,其开断短路电流时间较长,造成变压器、其他开关承受较长时间的短路冲击,严重影响设备安全[1]。因此, 需要一种快速断路器,能够在短路故障发生后迅速切断短路电流,缩短因系统短路引起的电压暂降时间,进而提高系统暂态稳定性[2]。目前,开断速度快、可靠性高的多断口真空断路器成为研究了热点[3-6]。基于永磁机构的快速真空断路器在配电网单相接地事故预防、电网短路限流、串联补偿等方面的得到了应用研究,取得了良好的社会效益和经济效益[7-8]。高电压等级、多断口的真空断路器已成为真空断路器未来的发展趋势[9]。
高电压等级的真空断路器通常采用多个断路器串并联的结构,采用快速斥力机构和相控开断技术实现快速开断。多断口真空断路器的整体开断特性受到每个断路器的影响,其主要因素为静态绝缘特性和动态均压特性[10]。真空灭弧室内的电场分布决定着断路器的开断能力,外部电场分布影响着断路器的整机绝缘特性。在断路器的设计和研发中,绝缘设计是其最基本问题,有限元分析是电场数值计算的一种高效的方法[11-13]。国内外许多学者采用数值计算方法对断路器的电场进行了计算和结构优化,文献[14-15]对40.5 kV和72.5 kV真空灭弧室电位和电场进行了计算和优化。沈阳工业大学对550 kV和1 100 kV的双断口SF6断路器电场进行了分析[16],武汉大学和大连理工大学分别对三断口和双断口模块化真空断路器的绝缘特性进行了仿真分析和试验[17-18],郑州大学对真空间隙与CO2气体间隙串联的混合不同结构下的电场进行了计算[19]。当额定电压不超过100~180 kV时,主要解决真空灭弧室内部电场分布问题;当电压等级大于180 kV时,真空断路器的研制需要对内、外电场进行计算,目前,尚未有对气体绝缘的363 kV真空断路器的研究和绝缘性能分析。
笔者提出了一种电压等级为363 kV,额定电流为5 000 A,额定开断电流为63 kA,分闸时间小于5 ms的快速真空断路器。该断路器采用多个40.5 kV断路器级联的方式,能够快速切断故障电流,降低短路电流对于线路中其他设备的热冲击和大电流冲击。断路器采用密闭式气体绝缘式结构,以SF6为外绝缘介质,真空灭弧室作为灭弧手段。为了校核断路器的绝缘特性,以363 kV快速真空断路器的设计模型为基础,充分考虑内部关键部件和复杂结构特点,建立快速断路器的多重介质三维电场数学模型,采用有限元方法对断路器的绝缘性能进行了计算与分析,为快速断路器的样机生产提供参考。
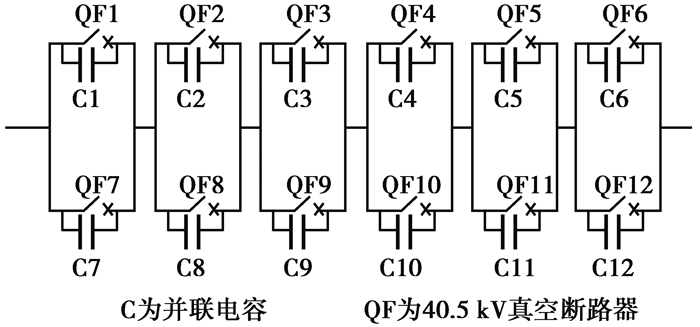
1 气体绝缘363 kV真空断路器结构363 kV电压等级的快速断路器整体样机如图 1所示,每相由2组6个串联的40.5 kV的真空断路器并联组成,主要包括真空灭弧室、操动机构、上下接线端、导电杆以及绝缘支撑等部件。每个断口并联了均压电容,实现均压作用。采用快速涡流斥力机构以及相控短路电流快速识别算法,断路器可实现在第一个半波(10 ms)内对短路电流的可靠快速开断。真空灭弧室、导电杆和操动机构等均放置于直径为0.8 m、高度为2 m的金属罐中,内部充满高气压的SF6气体作为绝缘介质。断路器整体设计结构如图 2所示,三维结构图和整体效果图如图 3所示。
|
图 1 363 kV真空断路器单相拓扑图 Figure 1 Single phase topology of 363 kV VCB |

|
图 2 363 kV真空断路器单相三维结构 Figure 2 Single phase 3D structure of 363kV VCB |

|
图 3 气体绝缘363 kV真空断路器整体效果图 Figure 3 Effect drawing of gas insulated 363kV VCB |
断路器整机为对称结构,每个断路器由商业的40.5 kV真空灭弧室和独立的操动机构构成,并采用分相控制,每个断口也是独立动作。同时整机采用了6个断口,对330 kV电网的应用留出了较大的电压裕度。因此,只需要对其中一组中间连接串联的两台单元以及两端的端部连接单元进行计算(考虑导电杆的高低布置不同)。外部罐体的尺寸为2 m高,内部真空灭弧室的屏蔽罩等部件的尺寸为1 mm,尺寸对比超过2 000倍,为了减少计算量和提高计算精度,需要对模型进行合理简化。断路器的电场分析考虑断口、绝缘部件的电场大小。因此,省略了波纹管、波纹管屏蔽罩,仅保留主屏蔽罩,灭弧室上下端盖以及陶瓷外壳简化为圆柱[4]。操动机构内部结构放置于接地的金属箱体内,内部的机械、电路结构并不影响外部电场,因此,省去了操动机构箱的内部结构,仅保留金属外壳结构。仿真模型中仅考虑了外壳、绝缘气体、真空灭弧室、导电杆、绝缘支撑、上下接线端和法兰,内部结构如图 4所示。仿真模型的基本参数如表 1所示。

|
图 4 仿真模型的几何结构 Figure 4 Geometry of simulation model |
| 表 1 仿真模型的基本参数 Table 1 Basic parameters for simulation model |
罐体内三维静电场计算区域满足拉普拉斯方程:
| $ {{\nabla }^{2}}\varphi =0。$ | (1) |
断路器含有多重绝缘介质材料,在不同绝缘介质的分界面上,电位满足如下边界条件:
| $ {{\varphi }_{1}}={{\varphi }_{2}}, $ | (2) |
| $ {{\varepsilon }_{1}}\frac{\partial {{\varphi }_{1}}}{\partial n}={{\varepsilon }_{2}}\frac{\partial {{\varphi }_{2}}}{\partial n}, $ | (3) |
式中:φ1、φ2为节点电位分界面两边不同物质的电位;ε1、ε2分别为分界面两边不同物质的相对介电常数;n为交界面的外法线矢量。对于灭弧室内部的屏蔽罩等悬浮电位物体,采用电压自由度进行耦合。
2.3 边界条件在灭弧室全部都闭合的情况下,触头、接线端子、导电杆等金属材料在工频交流电场作用下认为是良导体,计算时作为等势体处理。在仿真中导电杆、接线端等设置为高电位和终端,直接加载电压边界条件,外壳罐体接地,设置零电位灭弧室屏蔽罩为悬浮电位。高压断路器的绝缘水平需要满足工频耐受电压、操作冲击耐受电压和雷电冲击耐受电压试验的要求,根据《高压开关设备和控制设备标准的共用技术要求》[20],高压363 kV SF6断路器需达到的绝缘水平如表 2所示。仿真过程中在一端的导电部件加载型式实验电压值,而另一侧加载反向相电压峰值,并假定均压电容的均压效果理想,开断后每个断口的电压相等。
| 表 2 363 kV高压断路器绝缘水平 Table 2 Insulation level of 363 kV circuit breaker |
模型中主要考虑了动静触头、真空、屏蔽罩、瓷套、环氧绝缘支撑、操动机构控制箱外壳等部件。其中,真空断路器模块的动静触头为铜铬合金,屏蔽罩、灭弧室端盖、转接法兰、上下接线为钢,环氧支撑结构的材料为环氧树脂,灭弧室外壳为陶瓷。各部分材料的相对介电常数值如表 3所示。
| 表 3 材料相对介电常数 Table 3 Dielectric properties of the materials involved |
断路器的整机结构复杂,为保证计算精度和计算内存的大小,需要合理配置网格的尺寸。将模型分解为多个子域,根据子域内几何大小调整网格的尺寸,采用区域分解法进行全场域的四面体网格剖分。对灭弧室屏蔽罩等部件采取极细化剖分,对于大尺寸的结构进行粗化剖分,在保证网格质量的前提下尽可能提高计算效率。网格剖分如图 5所示,两个断路器剖分产生的顶点数为932 433个,四面体单元为5 532 588个。

|
图 5 计算场域的网格剖分 Figure 5 Meshes of the calculation domain |
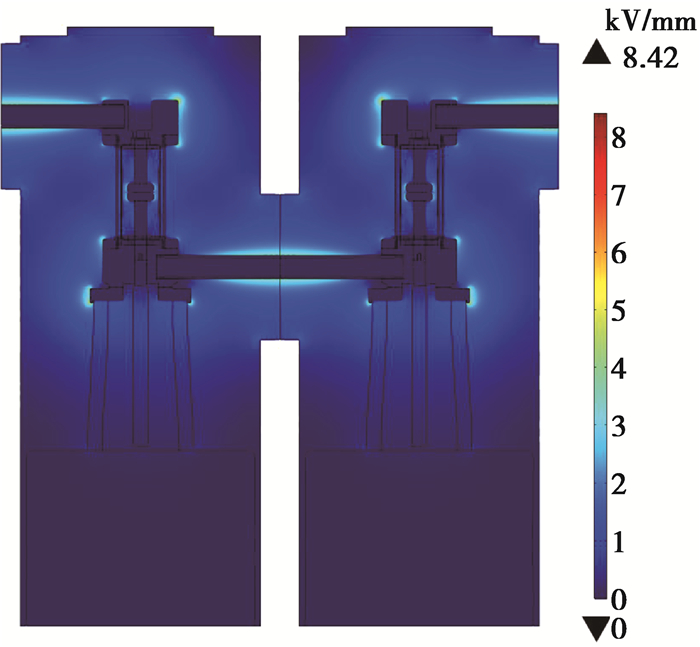
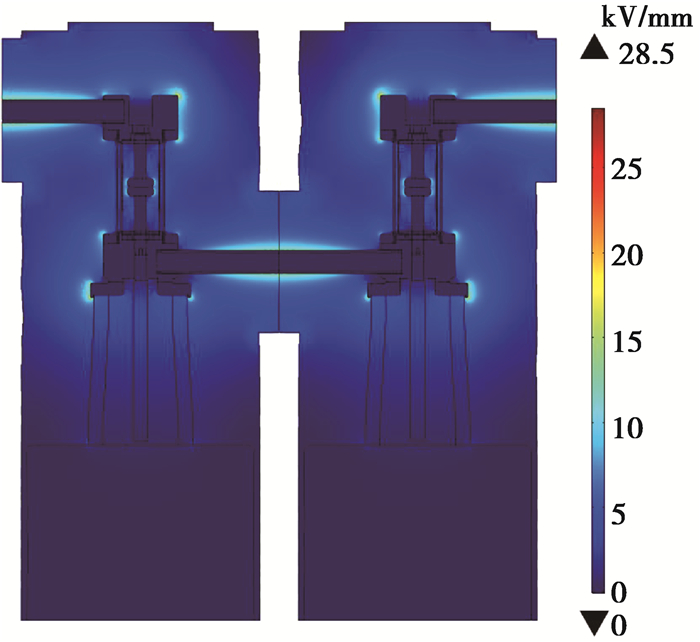
在断路器所有断口均闭合的情况下,施加额定电压的有效值和雷电冲击电压的峰值,分别对中间连接单元和端部连接单元进行仿真计算,计算得到的电场截面云图分布见图 6和图 7。
|
图 6 额定工况下断路器电场分布 Figure 6 Electric field distribution of VCB under rated voltage at closed state |
|
图 7 雷电冲击工况下断路器电场分布 Figure 7 Electric field distribution of VCB under lightning impulse voltage at closed state |
由图 6和图 7可知,断路器电场集中接线端子和法兰边缘。对于中间连接单元,在工频额定电压下,上接线端圆角表面和转接法兰下表面圆角处的电场最大值分别为8.42 kV/mm和7.3 kV/mm;雷电冲击电压下的电场最大值分别为28.5 kV/mm和22.9 kV/mm。对于端部连接单元,雷电冲击电压下的电场最大值分别为25.7 kV/mm和19.9 kV/mm。
雷电冲击电压下在0.6 MPa气压下SF6中导体表面电场控制值为33 kV/mm[21],因此,导体和接线端子的表面电场处于控制范围内,尺寸设计合理。圆角处的电场分布如图 8所示,圆周边缘出现了电场集中,这与圆角的大小和金属罐体与接线端子的距离有关。罐体的尺寸是基于操纵机构大小和电场分布确定的,同时,罐体顶部加高可以增大接线端子与零电位的距离,但是这样会极大增加断路器的体积和成本。接线端子的圆角边缘周围的电场迅速减小,因此,接线端子的圆角是可优化的部位。

|
图 8 上接线端圆角处电场分布 Figure 8 Electric field distribution of upper terminal circular bead |
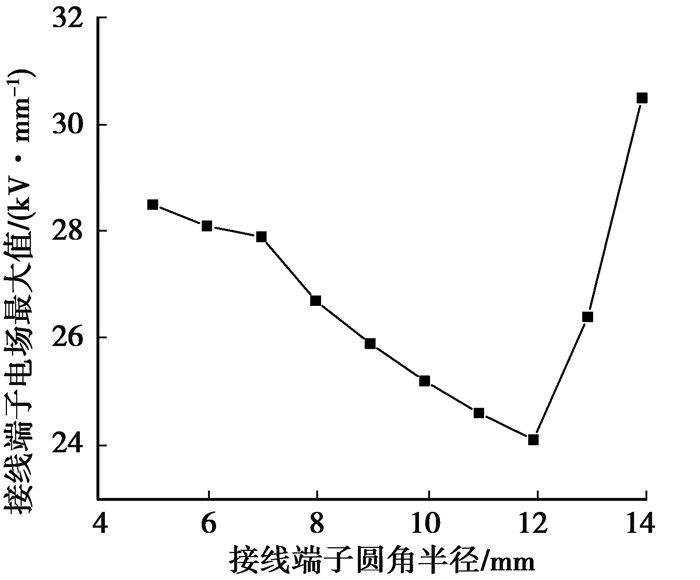
现有接线端子设计留出了较大的裕量,其圆角半径为5 mm,因此,将其圆角半径作为变量,进行参数化扫描仿真。圆角半径从5 mm开始,扫描步长为1 mm,一直扫描到14 mm,计算每个圆角半径下的电场值,得到电场值变化见图 9所示。当圆角半径大于14 mm时,接线端子与导电杆过于接近,出现尖锐结构,电场急剧增大,同时机械裕量也不足。因此,接线端子的圆角半径取值为12 mm左右最为合适,此时的电场强度为24.1 kV/mm。
|
图 9 接线端子电场最大值与圆角半径的关系 Figure 9 Relation between the maximum electric field and the radius of connecting terminals |
导电杆在断路器整机中起着载流和连接作用,其表面电场设计尤为重要。额定工况和雷电冲击电压下导杆表面电场分布见图 10和图 11,最大值位于两个罐体的连接处,分别为3.78 kV/mm和13.4 kV/mm。由于连接处的外壳半径为0.25 m,离导杆的距离较近。

|
图 10 额定电压下导电杆电场分布 Figure 10 Electric field distribution of conductor under rated voltage |

|
图 11 雷电冲击工况下下断路器导电杆电场分布 Figure 11 Electric field distribution of conductor under lightning impulse voltage |
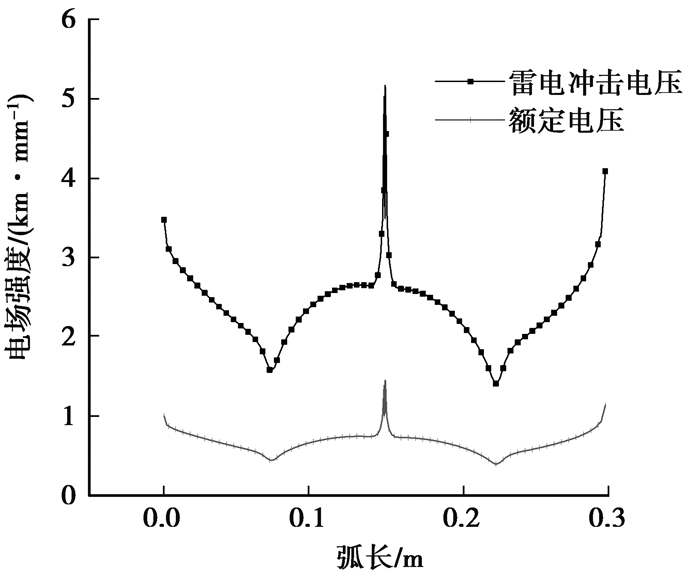
灭弧室陶瓷外壳沿面电场取值方法和电场分布如图 12和图 13所示,结合整体电场分布云图可知,雷电冲击电压下最大电场值位于屏蔽罩与陶瓷外壳交接处,达到了5.1 kV/mm,远低于控制值16.5 kV/mm[21]。灭弧室内部电场集中于触头倒角处和屏蔽罩终端,最大值分别为9.1 kV/mm和10.8 kV/mm。

|
图 12 灭弧室表面电场取值线 Figure 12 Sampling line on the VCB surface |
|
图 13 灭弧室沿线电场分布 Figure 13 Electric field distribution of insulating envelope |
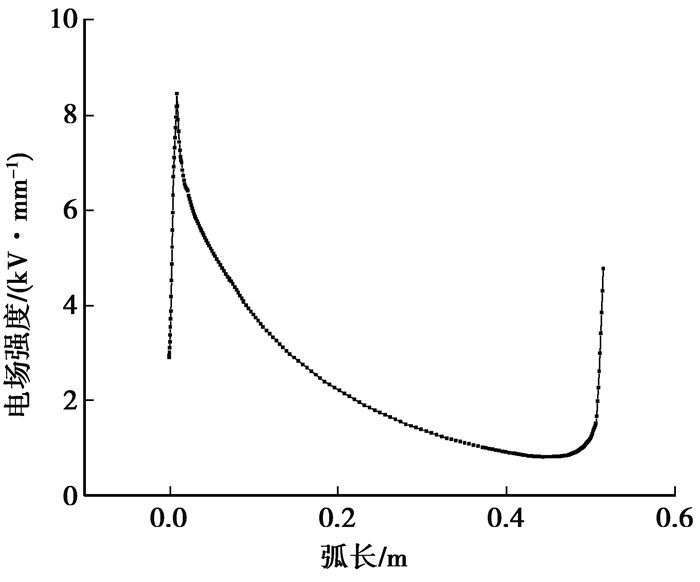
断路器中的绝缘件表面电场在雷电冲击电压下不能超过控制值。沿环氧绝缘支撑台表面取一条线,分析其表面电场,见图 14,计算得到的沿线表面电场如图 15所示。最大值的位置靠近转接法兰的圆角处,在支撑绝缘台下表面50 mm处电场出现最大值,最大值为8.45 kV/mm,远小于控制值14 kV/mm[21]。

|
图 14 环氧绝缘支撑台采样线 Figure 14 Sampling line on the epoxy insulator surface |
|
图 15 v Figure 15 Electric field distribution of epoxy insulator surface |
根据标准规定,断路器在全开距即分闸位置的情况下,断口属于隔离开断断口,需满足断口下的雷电冲击电压绝缘水平。断路器采用的是40.5 kV商业真空灭弧室,能够承受的雷电冲击电压为230 kV。在均压电容的作用下,灭弧室断口内部电场能够符合要求。因此,重点分析开断后灭弧室外壳的绝缘性能。
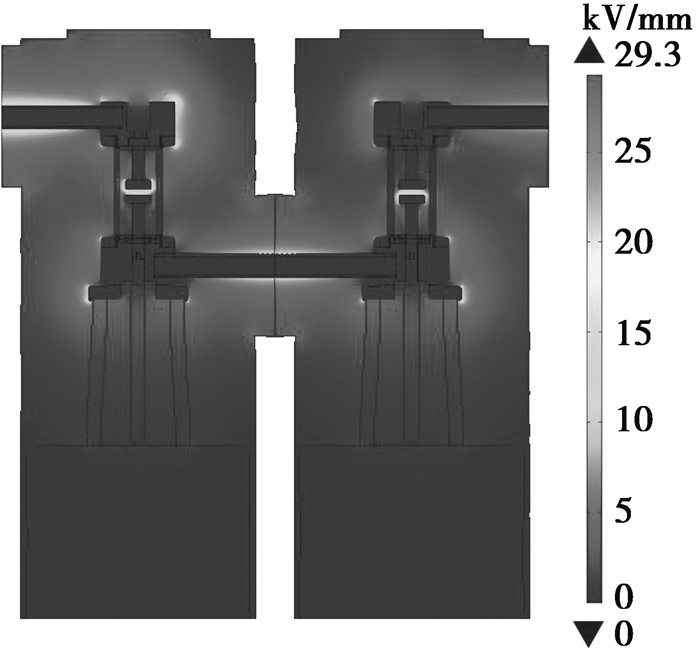
在全开距情况下,每个灭弧室都处于完全分闸位置,每个灭弧室断口承受的电压接近,但是各自电位差距很大,第一个灭弧室的触头电位最高。在第一个灭弧室的静触头加载电位为1 050 kV,在动触头、下接线端子和导杆加载电位为840 kV。第二个灭弧室静触头加载电位为630 kV,电场计算结果如图 16所示。
|
图 16 v Figure 16 Electric field distributions of 363 kV VCB at open state |
由图 16可知,电场最大值仍位于上接线端子圆角边缘处,达到了29.3 kV/mm。其次,触头边缘电场较大,达到了26.9 kV/mm,由于触头处于真空环境中,此时的真空灭弧室的耐受为35 kV/mm[14],处于控制范围内。
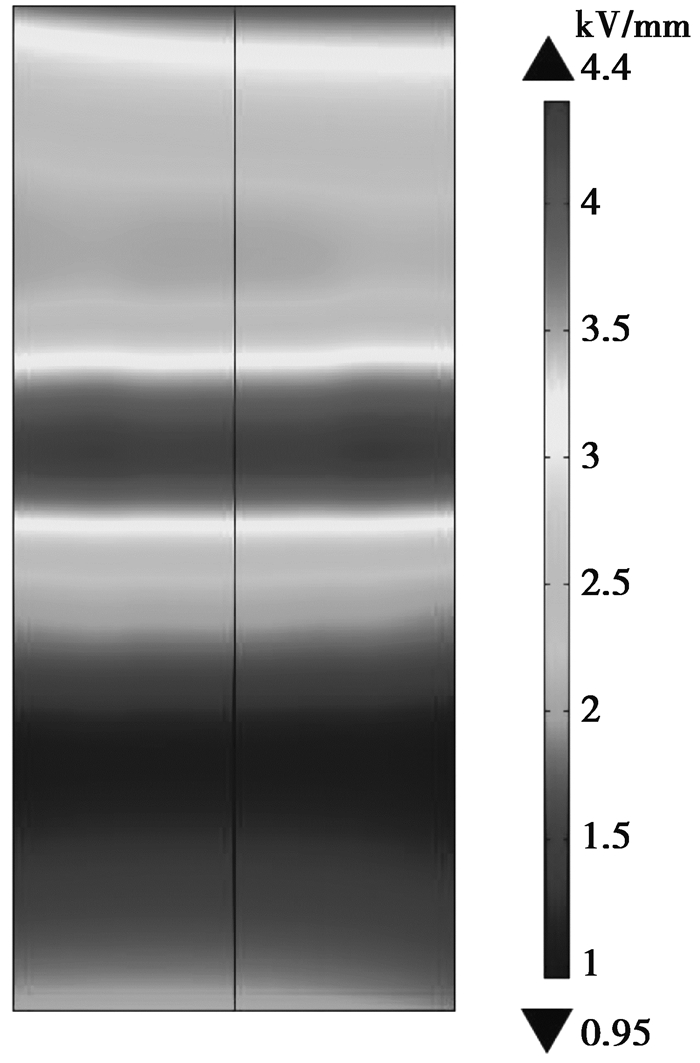
灭弧室陶瓷外壳表面电场见图 17所示,中间位置即触头所处的对应位置电场比较集中,达到了4.4 kV/mm,远低于SF6气体中绝缘件表面电场的控制值16.5 kV/mm。
|
图 17 开断状态下灭弧室陶瓷外壳电场分布 Figure 17 Electric field distributions of VCB's envelope at open state |
针对真空断路器应用于高压电网限制短路电流中的问题,提出了一种具有串并联结构的气体绝缘363 kV真空断路器结构。根据断路器绝缘型式实验标准规定的电压要求,采用有限元法计算了整机闭合和开断下的三维电场分布,计算结果表明:闭合和开断情况下,电场均集中于接线端子和转接法兰圆角边缘处,雷电冲击电压下的电场值达到了29.3 kV/mm和28.5 kV/mm。对接线端子的圆角半径进行了优化,其最优半径为12 mm,此时的电场值为24.1 kV/mm。真空灭弧室内部电场处于真空击穿场强控制范围内。灭弧室陶瓷外壳和环氧支撑绝缘台的表面电场最大值分别为5.1 kV/mm和8.45 kV/mm,在绝缘允许范围内。气体绝缘363 kV真空断路器的电场也均在绝缘允许范围内,计算结果可为气体绝缘高电压等级真空断路器的生产提供参考。
| [1] |
Zhang B, Li R, Ding J, et al. A relationship between minimum arcing interrupting capability and opening velocity of vacuum interrupters in short-circuit current interruption[J]. IEEE Transactions on Power Delivery, PP(99): 1-1. |
| [2] |
周念成, 刘家伟, 赵渊, 等. 消弧线圈接地系统暂态能量选线新方法[J]. 重庆大学学报, 2009, 32(12): 1425-1430. ZHOU Niancheng, LIU Jiawei, ZHAO Yuan, et al. Novel method for fault line selection in arc suppression coils system using transient energy[J]. Journal of Chongqing University, 2009, 32(12): 1425-1430. (in Chinese) DOI:10.11835/j.issn.1000-582X.2009.12.011 |
| [3] |
Ide N, Tanaka O, Yanabu S, et al. Interruption characteristics of double-break vacuum circuit breakers[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2008, 15(4): 1065-1072. |
| [4] |
Huang D, Wu G, Ruan J, et al. Study on static and dynamic voltage distribution characteristics and voltage sharing design of a 126-kV modular triple-break vacuum circuit breaker[J]. IEEE Transactions on Plasma Science, 2015, 43(8): 2694-2702. DOI:10.1109/TPS.2015.2449075 |
| [5] |
Cheng X, Chen Z, Ge G, et al. Dynamic dielectric recovery synergy of hybrid circuit breaker with CO2 gas and vacuum interrupters in series[J]. IEEE Transactions on Plasma Science, 2017, PP(99): 1-8. |
| [6] |
Yao X, Wang J, Geng Y, et al. Development and type test of a single-break 126-kV/40-kA-2500-A vacuum circuit breaker[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 182-190. DOI:10.1109/TPWRD.2015.2456033 |
| [7] |
艾绍贵, 马奎, 吴旭涛, 等. 快速真空断路器在电力系统中的应用[J]. 电工电气, 2016(5): 1-5. AI Shaogui, MA Kui, WU Xutao, et al. Application of fast vacuum circuit breaker in electric system[J]. Electrotechnics Electric, 2016(5): 1-5. (in Chinese) DOI:10.3969/j.issn.1007-3175.2016.05.001 |
| [8] |
艾绍贵, 马奎, 贺好艳, 等. 一体化集成变阻抗节能变压器的研究[J]. 高电压技术, 2016, 42(4): 1028-1034. AI Shaogui, MA Kui, HE Haoyan, et al. Research on integrated variable impedance energy-saving transformer[J]. High Voltage Engineering, 2016, 42(4): 1028-1034. (in Chinese) |
| [9] |
吴高波, 阮江军, 黄道春, 等. 多断口真空断路器均压电容研究综述[J]. 高压电器, 2011, 47(3): 77-81. WU Gaobo, RUAN Jiangjun, HUANG Daochun, et al. Review of grading capacitors of multi-break vacuum circuit breakers[J]. High Voltage Apparatus, 2011, 47(3): 77-81. (in Chinese) |
| [10] |
Huang D, Shu S, Ruan J. Transient recovery voltage distribution ratio and voltage sharing measure of double-and triple-break vacuum circuit breakers[J]. IEEE Transactions on Components Packaging & Manufacturing Technology, 2016, 6(4): 545-552. |
| [11] |
李俐莹, 刘晓明. 能量分离喷口高压SF6断路器灭弧室电场分析[J]. 电工技术学报, 2015, 30(13): 56-62. LI Liying, LIU Xiaoming. Analysis on the electrical field of high voltage SF6 arc quenching chamber with energy separation nozzle[J]. Transactions of China Electrotechnical Society, 2015, 30(13): 56-62. (in Chinese) DOI:10.3969/j.issn.1000-6753.2015.13.008 |
| [12] |
唐治德, 刘海龙, 陈秀发, 等. 容积导电能量传递多场耦合数值模拟[J]. 重庆大学学报, 2013, 36(1): 69-74. TANG Zhide, LIU Hailong, CHEN Xiufa, et al. Multi-field coupled numerical simulation of volume conduction energy transfer[J]. Journal of Chongqing University, 2013, 36(1): 69-74. (in Chinese) |
| [13] |
汪朝晖, 廖振方, 陈德淑. 有限元法分析尖板电极结构的空间静电场分布[J]. 重庆大学学报, 2010, 33(5): 41-47. WANG Zhaohui, LIAO Zhenfang, CHEN Deshu. Analysis of spatial electric field with point-plate electrodes configuration using finite element method[J]. Journal of Chongqing University, 2010, 33(5): 41-47. (in Chinese) |
| [14] |
杨敬华, 范承勇. 40.5kV真空断路器绝缘结构电场分析及优化设计[J]. 电网技术, 2011, 35(12): 146-152. YANG Jinghuan, FAN Chengyong. Electric field analysis and optimization design of insulation structure of 40.5 kV vacuum circuit-breaker[J]. Power System Technology, 2011, 35(12): 146-152. (in Chinese) |
| [15] |
邱志斌, 黄道春, 阮江军. 72.5kV真空灭弧室电位和电场分布研究[J]. 高压电器, 2012, 48(11): 36-42. QIU Zhibin, HUANG Daochun, RUAN Jiangjun. Potential and electric field distributions of 72.5 kV vacuum interrupter[J]. High Voltage Apparatus, 2012, 48(11): 36-42. (in Chinese) |
| [16] |
Fu S, Cao Y, Wang B, et al. Three dimensional electric field in a novel rotary-gas nozzle structure of SF6 circuit breaker[C]/[KG-0. 5mm]/Power and Energy Engineering Conference. IEEE, 2010: 1-4.
|
| [17] |
黄道春, 阮江军, 吴高波, 等. 具有串并联结构的模块化多断口真空断路器静动态电压分布特性[J]. 电网技术, 2011, 35(7): 181-186. HUANG Daochun, RUAN Jiangjun, WU Gaobo, et al. Study on static and dynamic voltage distribution characteristics of modularized multi-break vacuum circuit breaker with series and parallel configuration[J]. Power System Technology, 2011, 35(7): 181-186. (in Chinese) |
| [18] |
Liao M F, Ge G W, Duan X Y, et al. Influence of the AMF arc control on voltage distribution of double-break VCBs[J]. IEEE Transactions on Plasma Science, 2016, 44(10): 2455-2461. DOI:10.1109/TPS.2016.2603532 |
| [19] |
程显, 焦连曜, 葛国伟, 等. 真空间隙与CO2气体间隙串联的混合断路器电场仿真计算[J]. 真空科学与技术学报, 2016, 36(12): 1356-136. CHENG Xian, JIAO Lianyao, GE Guowei, et al. Simulation of electric field distributions in vacuum/CO2 gaps of hybrid circuit breaker[J]. Chinese Journal of Vacuum Science and Technology, 2016, 36(12): 1356-1362. (in Chinese) |
| [20] |
国家能源局. 高压开关设备和控制设备标准的共用技术要求: DL/T 593-2016[S]. 北京: 中国电力出版社, 2016. National Energy Administration. Common specifications for high-voltage switchgear and controlgear standard: DL/T 593-2016[S]. Beijing: China Electrical Power Press, 2016. (in Chinese) |
| [21] |
黎斌. SF6高压电器设计[M]. 4版. 北京: 机械工业出版社, 2015. LI Bin. SF6 high voltage electrical design[M]. 4th edition. Beijing: China Machine Press, 2015. |
 2018, Vol. 41
2018, Vol. 41

