2. 江西铜业集团银山矿业有限责任公司, 江西 德兴 334200
2. Yinshan Mining Co., Ltd, Jiangxi Copper Group, Dexing 334200, Jiangxi, P. R. China
在地下开采过程中,矿体的开挖打破了原岩应力场的平衡状态,导致开挖区域周围岩体的应力重新分布[1-3]。通过合理安排、调整回采顺序,可以显著改变开挖后围岩的应力分布状态,在很大程度上提高采场的稳定性[4-5]。为满足产量要求,需要多个矿块同时回采,由于多中段同时生产技术要求高,管理复杂,安全问题突出,因此,随着矿山产能的不断提高,同一中段多矿块同时回采成为必然趋势。传统的相邻矿块间回采顺序一般采用平行推进的方式,即多个矿块同步回采,矿山生产过程中发现,该回采方式由于中央采场产生严重的局部拉应力集中现象,顶板冒落等安全事故时有发生,存在较大的安全生产隐患。因此,通过合理安排矿块间的回采顺序,改善开挖后围岩的应力分布状态,对提高采场的稳定性和回采工作面的安全性具有一定的工程价值[6-7]。
国内外许多专家对回采顺序优化进行了多方面研究,传统的相似模型试验[8]、半工业试验以及现场工业试验[9]都会消耗大量的人力、物力和财力,且很难实现多种回采方案的比较。随着矿山岩石力学理论以及数值模拟技术的快速发展,数值模拟已成为分析地下开采时采场稳定性行之有效的方法[10-11]。目前,国内外已研发出多款较为成熟的有限元计算软件用于岩土工程分析,如FLAC3D、ANSYS、ADINA、RFPA2D、MIDAS/GTS等。杨玉学等[12]运用FLAC3D对矾山磷矿的阶段回采顺序进行了数值模拟,选取了合理的回采方案;王李管等[13]构建了采场回采顺序优化的混合整数规划模型,求解得到采场回采顺序的最优布置方案;叶义城等[14]通过构建相似模型对嗣后充填采矿法回采上横山矿的回采顺序进行探究。现阶段对回采顺序的优化研究主要是矿山整体开采推进顺序(即上行式、下行式等),对相邻矿块间的回采顺序优化研究较少,且并未对不同的回采顺序给出合理的解释。鉴于以上分析,笔者以新桥矿为例,结合数值模拟方法,将压力拱理论引入到模拟结果的对比分析中,提出最佳的矿块间回采顺序。
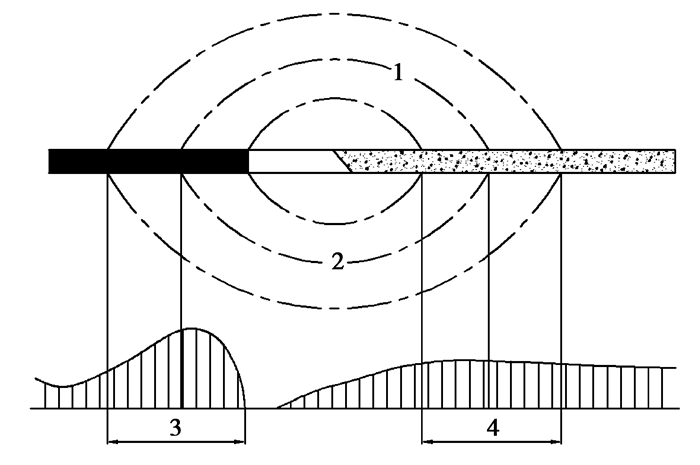
1 压力拱理论岩体开挖后,洞壁岩体失去了原有岩体的支撑,破坏了原有的受力平衡和载荷传递路径;在重力场和初始应力场的作用下,围岩发生新的变形,应力、应变和能量进行自发调整,并最终达到一个新的平衡状态;此时由于围岩中各处变形的不均匀性,硐室周边一定岩体厚度范围内的围岩将产生类似于拱结构切向压紧的作用,这就是压力拱理论[15-16](见图 1)。压力拱效应是岩体为抵抗岩体开挖后产生的不均匀变形而进行自我调节的一种现象,是因围岩内应力发生集中、传递路线发生偏转而形成的一种拱形应力分布区。重分布应力场中,开挖面周围主应力方向发生偏转,其最大主应力流线形成一个环状体。压力拱的形成改变了介质中原有载荷的传递状态,它能够把作用于拱后或拱上的压力传递到拱脚及周围稳定介质中,并充分发挥了岩土材料良好的受压性能。它的主要特点是,地下工程开挖后,主应力方向发生偏转,但无破裂发生;受力特征为截面无弯矩和拉应力,其受力主要是压应力,并且相对于原岩应力来说,切向应力增大,径向应力减小。压力拱内的围岩承担着其自身和上覆岩土的载荷,是确保其洞室围岩不会塌落的一个具有拱的力学特性的结构[17-18]。压力拱是工程开挖引起应力转移的一种常见形式。
|
图 1 回采工作面压力拱 Figure 1 Pressure arch hypothesis around the working face 1—顶板内压力拱轴线;2—底板内压力拱轴线; 3—前拱脚;4—后拱脚 |
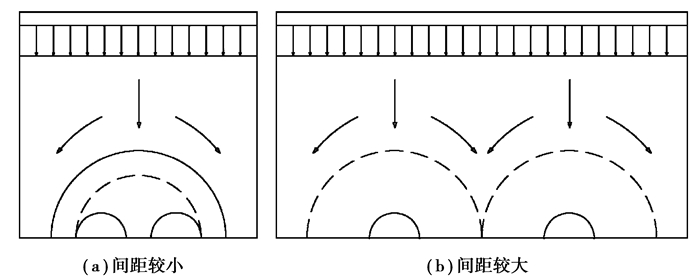
Anwar[19]研究了双隧道埋深和间距与压力拱的关系,研究认为双隧道间距较小时,形成一个压力拱;间距较大时,形成2个独立的压力拱(见图 2)。
|
图 2 双隧道围岩压力拱 Figure 2 Pressure arches in surrounding rock near the double tunnels |
新桥矿矿体产状为层状,平均倾角25°,平均厚度25 m。现矿体已开采至-300 m水平,主体采矿方法为机械化上向水平分层充填法[20]。按照两步骤回采工艺,垂直走向交替布置矿房、矿柱,先采矿柱(10 m),胶结充填后回采矿房(14 m),进行非胶结充填。
为满足矿山产能要求,矿山研究需进行临近多矿块同时开采,并自行试验了相邻3个矿块同时平行回采,试验过程中发现中央采场出现比较严重的局部拉应力集中现象,容易导致较严重的片帮、冒顶等安全事故。由于作业人员和设备频繁暴露于空场下进行作业,所以必须改善采场的安全作业条件。因为前期工程已施工完毕,更改采场结构参数对矿山生产影响较大,为保证矿山生产的安全进行,研究对矿块间回采顺序进行优化。
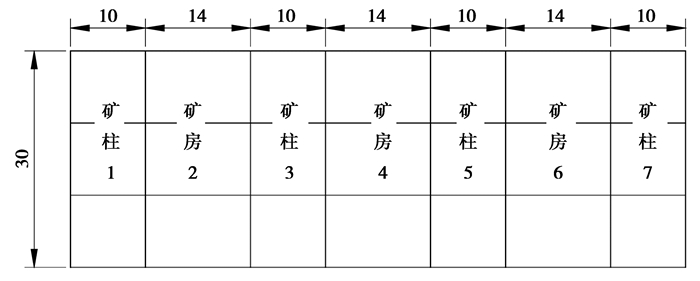
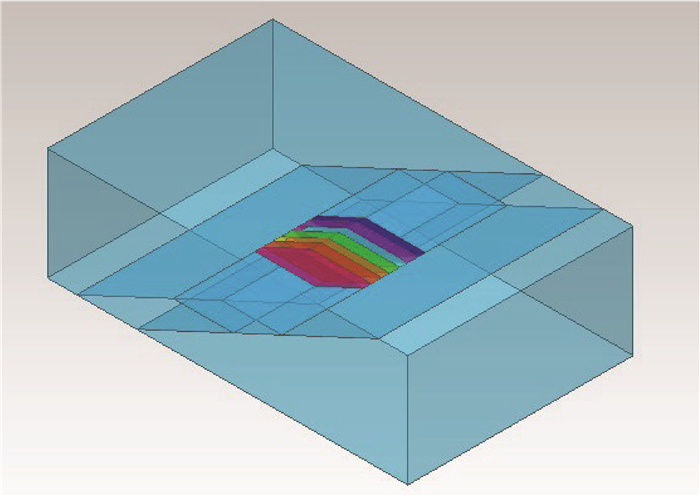
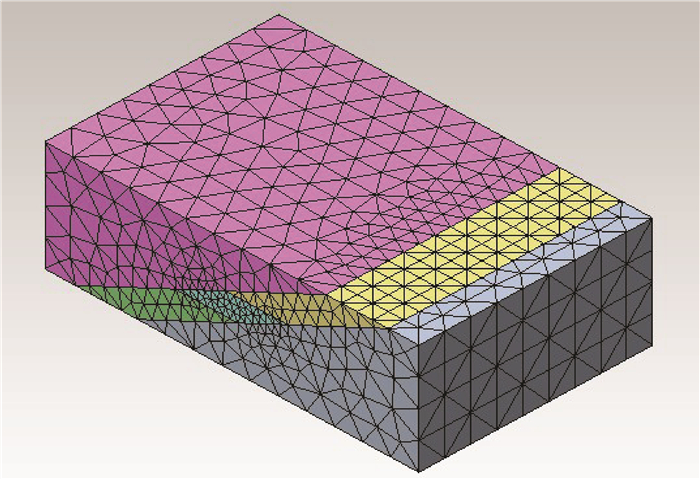
2.2 模型建立考虑矿体赋存的实际情况及数值模拟对计算机软硬件的要求,选取具有代表性的-300 m中段的3个矿房和4个矿柱,矿房宽度为14 m,矿柱宽度为10 m(图 3),矿体倾角为25°。根据圣维南原理,围岩足够大才能消除局部效应的影响,取模型尺寸为矿体尺寸的3~5倍,且在走向方向上全部简化为矿体。建立的数值计算模型尺寸为x×y×z=480 m×150 m×300 m,划分网格共有15 602个节点和103 803个四面体单元。在此情况下,网格疏密划分合理,研究重点网格适当加密,各项结果数据随网格划分影响不显著,故而保证了模拟结果的精确性。模型边界条件采用位移约束方式:模型四周和底部边界进行位移约束,且由于该矿群埋深270 m左右,模型没有建到地表,顶部施加4 500 kPa的压力荷载。三维实体模型如图 4所示,网格划分模型如图 5所示。
|
图 3 矿房矿柱布置 Figure 3 Layout of rooms and pillars |
|
图 4 三维实体模型 Figure 4 Three-dimensional solid model |
|
图 5 网格划分模型 Figure 5 Mesh model |
数值计算分析的准确性很大程度上取决于矿岩体基本力学参数是否准确。本次模拟采用的矿岩力学参数通过室内岩石力学试验获取,主要包括单轴抗压强度试验、抗拉强度试验、单轴压缩变形试验,所得数据经Hoek-Brown准则折减后的矿岩力学参数,如表 1所示。
| 表 1 矿岩力学参数 Table 1 Mechanical parameters of ore rock |
上向水平充填采矿法的一般步骤:两步骤回采,先回采矿柱,胶结充填后回采矿房,最后进行非胶结充填,开挖顺序为由下至上。根据矿山现有条件,提出3种矿块间的回采方案。
方案一:矿房矿柱均同时平行开采,该方案的优点在于矿房矿柱布置简单,回采作业时可平行推进,凿岩、爆破、出矿作业集中,易于管理,效率较高;主要缺点为矿房矿柱回采过程中尤其是爆破作业相互影响较大,尤其是中间的采场,不利于采场的稳定,易造成采场的冒落、片帮。新桥矿自行试验了该方案,中央采场出现比较严重的局部拉应力集中现象,容易导致较严重的片帮、冒顶等安全事故。
方案二:矿房矿柱均按“品”字形结构布置,该方案的优点在于每个上部采场位于下部两个采场的间隔的上部,采场之间的回采作业相互影响较低,回采完成之后应力重新分布分散,不会产生应力集中现象,有利于采场的稳定;主要缺点为采场分散,不易于作业管理,效率相对较低。
方案三:矿房矿柱均按倒“品”字形结构布置,该方案的优缺点与方案二的相同,不同之处在于开挖之后的应力重新分布范围及状态,故而采场的稳定状态将会产生一定的差异。
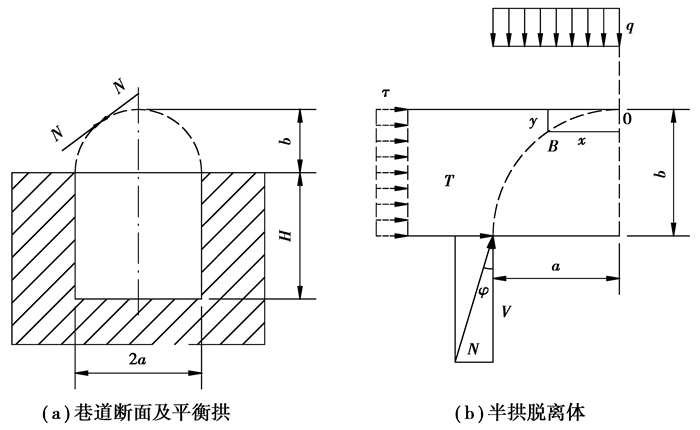
根据压力拱理论,由于压力拱效应,顶部可能冒落的岩石拱高为b,而拱周围岩体相互挤压[21-22]。取半拱脱离体如图 6所示,对拱列出弯矩平衡式,可以得到处于安全平衡状态时的拱高:
| $ b = \frac{a}{{\tan \mathit{\Phi '}}} = \frac{a}{f}。$ | (1) |
|
图 6 巷道压力平衡拱及其计算图 Figure 6 Roadway pressure balance arch and its calculation |
则顶部压力密度为:
| $ q = \gamma b = \frac{{\gamma a}}{{\tan \mathit{\Phi '}}} = \frac{{\gamma a}}{f}。$ | (2) |
总顶压为:
| $ {Q_{\rm{d}}} = 2\gamma ab = 2aq = \frac{{2\gamma {a^2}}}{f}。$ | (3) |
由式(3)可知,拱高、顶压都与巷道跨度和岩石坚固性系数有关,巷道跨度越大顶压就越大,稳定性就越差。
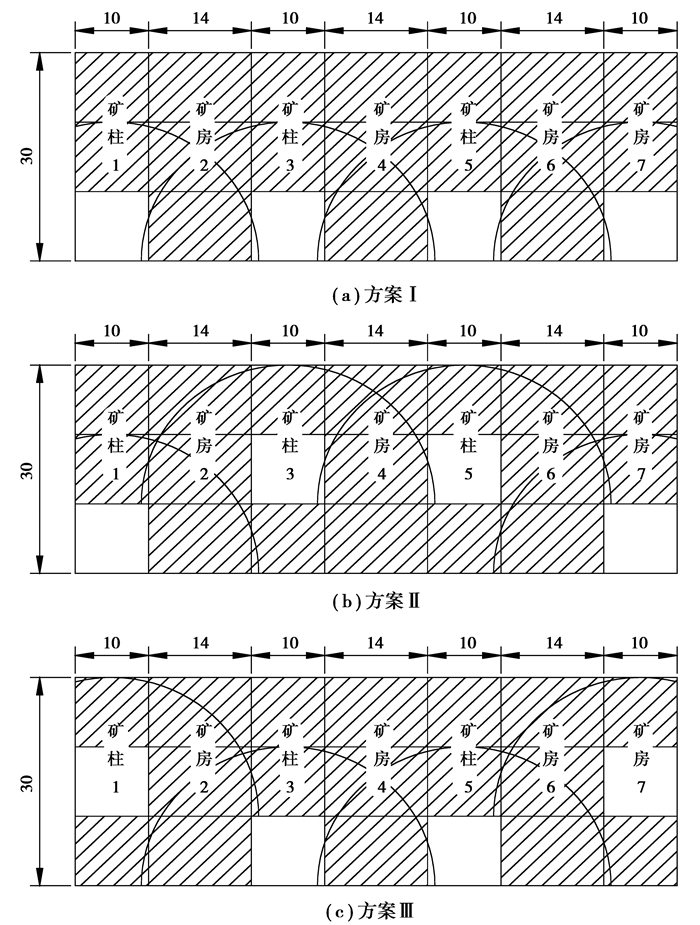
以上为单个巷道开挖之后压力拱效应分析。考虑岩体构造的影响,地下巷道开挖之后的影响区域为巷道直径的3~5倍范围,认为在这个范围以外认为岩体让处于原岩应力状态。在巷道跨度与岩石坚固性系数一定的情况下,由3种开采方案开采形成的压力拱效应之间的相互影响如图 7所示(由于开挖过程比较复杂,故而只对开挖初期进行分析)。
|
图 7 各方案回采形成的压力拱示意图 Figure 7 Diagram of the pressure arches formed by each program |
由拱效应影响图可以看出,方案Ⅰ每相邻两个采场开挖之后形成的拱效应区域相互影响范围很广,间隔的矿房整个都在影响范围内,且影响到同时开挖的采场,对上一分层的采场的开挖也会产生较大影响。故而易产生冒落、片帮等情况,不利于采场的稳定;方案Ⅱ开挖之后,只有上一分层两个采场之间的拱效应相互影响较大,会产生较大的顶压,与下一分层两个采场的拱效应相互影响很小,故而能够保障同时开挖的各个采场的稳定;方案Ⅲ开挖之后,同时开挖的采场之间的相互影响与方案Ⅱ相同,但是方案Ⅲ的一分层开挖将会对产生较大顶压的二分层的后续开挖产生较大影响,不利于后续的开挖。
具体回采步骤如表 2所示。利用MIDAS/GTS力学分析软件进行3种开采方案的模拟,进一步分析各个开采方案的应力及位移变化状态,进而综合对比。
| 表 2 各方案回采顺序 Table 2 Stoping sequence of each option |
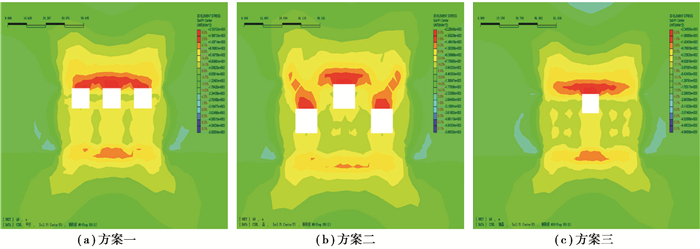
运用Midas模拟的计算结果信息量比较大,不能全部列出,只能给出关键部位、关键步骤的关键数据。各方案模拟结果见图 8~10,统计各个方案中出现的最大拉应力、最大压应力和最大位移情况汇总于表 3。
|
图 8 最大拉应力分布图 Figure 8 Distribution diagram of the maximum tensile stress |

|
图 9 最大压应力分布图 Figure 9 Distribution diagram of the maximum compressive stress |
|
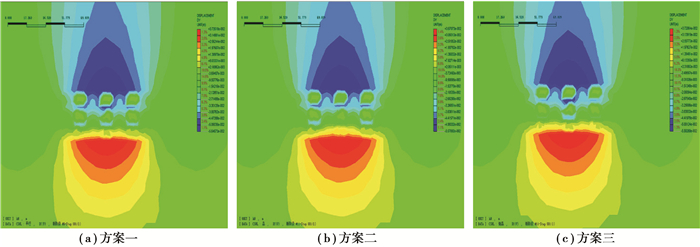
图 10 最大位移分布图 Figure 10 Distribution diagram of the maximum displacement |
| 表 3 各方案数值模拟结果 Table 3 Numerical simulation results of each option |
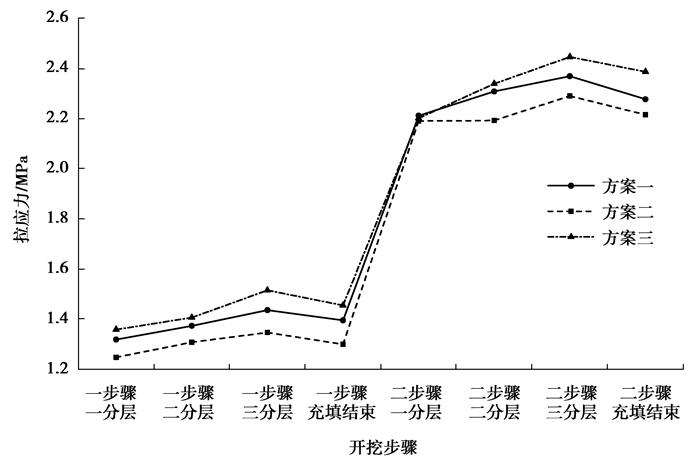
将上述3种方案拉应力、压应力和位移情况随回采步骤的变化绘制成曲线(图 11~13)。图 11~13及数值模拟结果表明:
|
图 11 最大拉应力变化曲线 Figure 11 The maximum tensile stress curve |
|
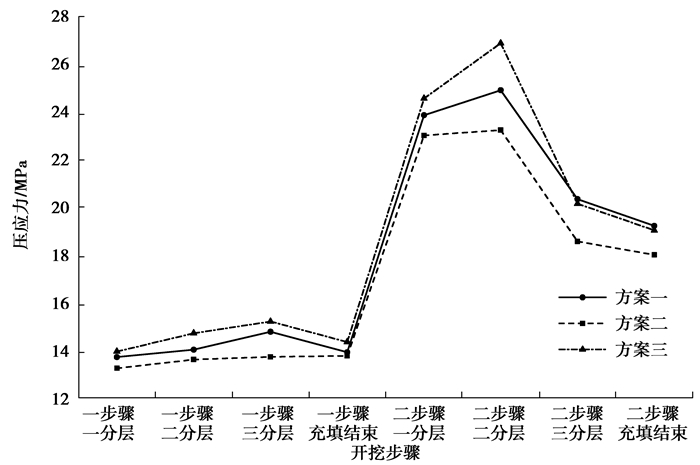
图 12 最大压应力变化曲线 Figure 12 The maximum compressive stress curve |
|
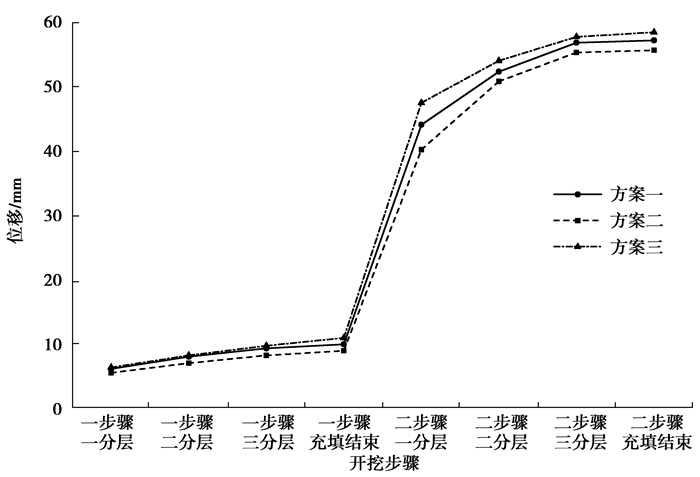
图 13 最大位移变化曲线 Figure 13 The maximum displacement curve |
1) 随着开采的不断推进,采场顶板和底板出现沉降和鼓起,采场顶板和底板位置出现拉应力,矿柱和四周矿体位置出现压应力。方案Ⅰ和方案Ⅱ的最大拉应力出现在中间采场的顶板处,方案Ⅲ的最大拉应力出现在两侧采场的顶板处。采矿过程中,在地下形成采空区,破坏了原岩体的应力平衡,使得采空区上部岩体由三维应力状态变为二维应力状态,顶板处横向应力由压应力变为拉应力,在上覆岩体作用下,顶板弯曲下沉;上覆岩体的载荷转移到采空区两侧的矿房、矿柱和矿体处,出现压应力。
2) 由应力分布图可以看出,方案二各分层的拉应力、压应力均小于方案一和方案三,且拉应力分布范围明显减小。
根据压力拱理论,矿体开挖之后,围岩中的应力重新分布,在每个采空区上方都会形成一个压力拱,将上覆岩体的载荷转移到所采区域之外,使得采空区内应力降低,改善了岩体的应力分布状态。且随着采空区的增加,压力拱的外边界向岩体深部移动,当相邻采空区的距离较小或者采空区增加时,其上部相邻的多个压力拱会构成一个更大的压力拱,将上覆岩体载荷转化为拱的切向应力,并将其传递至两侧矿柱。与方案一相比,方案二的中间矿柱(矿房)超前于两侧矿柱(矿房),采空区周围形成的压力拱也会更大,有利于与相邻的压力拱构成一个更大的压力拱,其将来自原岩的载荷传递到相邻矿柱(矿房)上部,进而转移到所采区域之外,使得回采工作处于应力降低区,避免了顶板冒落现象的出现,控制了上覆岩体的位移距离,保证了回采作业的安全。方案三中由于两侧矿体先进行回采,两个采空区相距较远,只能在各自采空区上部形成压力拱。采空区上部的压力拱会将部分原岩中的载荷转移到中间未采的矿柱(矿房),增大了中间的矿柱(矿房)的回采难度。
3) 各方案的最大拉应力均出现在三分层回采结束时,最大拉应力值分别为2.358,2.288,2.345 MPa;各方案的最大压应力均出现在二分层回采结束时,最大压应力值分别为24.91,23.24,26.88 MPa;各方案的最大位移均出现在充填结束时,最大位移值分别为56.48,55.71,55.83 mm。
充填体充填采空区时,一般都有一段固结和压密的过程,并不能马上起到支撑顶板作用,主要用于改善两侧矿柱的受力状态。随着采空区和空顶时间的增长,采空区顶板所受的拉应力不断增加,故最大拉应力值出现在三分层回采结束时。二分层回采结束时,矿柱所承受的覆岩体载荷最大,故最大压应力出现在二分层回采结束时。由于充填体与覆盖岩层或岩石之间有一定的空顶距离,顶板仍然处于沉降状态,故最大位移出现在充填结束时。
4) 与一步骤回采相比,二步骤回采的拉应力、压应力和位移均明显增加,增幅分别为0.7~1 MPa、5~10 MPa、35~47 mm。
二步骤回采的矿房宽度大于一步骤回采的矿柱宽度,且二步骤回采过程中,采场两侧矿柱为充填体,由于充填体的强度低,刚度小,与原有岩石相比,对阻止围岩变形的作用有限。同时一步骤充填结束时,存在一定的空顶距离,充填体未与顶板相接,起到的支撑作用有限。
5) 在充填结束时各方案的拉应力、压应力均出现不同程度的减小。
充填体充填空区改变了围岩中的应力分布状态,部分应力转移到充填体上,减缓了采空区顶底板受拉伸作用,使得矿柱处于三向受力状态,故拉应力、压应力均出现不同程度的减小。
4 结论1) 将压力拱理论与数值模拟手段相结合,通过压力拱理论对数值模拟结果的理论分析,以得到合理的开采顺序,进而以最优的开采顺序开采,从而使回采工作更安全高效,稳定性提高,降低开采风险。
2) 根据矿山现有条件,提出3种矿块间的回采顺序方案,即平行推进、“品”字形推进、倒“品”字形推进。
3) Midas数值模拟结果表明,不同回采顺序对回采过程中应力分布、位移变化有着不同程度的影响;“品”字形回采的最大拉应力、最大压应力、最大位移均远小于其他2种方案,有利于保证采场作业的安全。
4) 在方案二中,先进行中间矿房或矿柱一分层的回采,会在采空区上方形成一个压力拱;再进行中间矿房或矿柱二分层时会在采空区上部形成一个更大的压力拱,与回采两侧矿房或矿柱形成的压力拱构成一个较大的压力拱,承担其自身和其上覆的岩土载荷。
5) 新桥矿的生产实践表明:较矿山之前的矿块回采顺序而言,在采用“品”字形矿块回采顺序之后,采场并未出现安全事故,并取得了良好的经济、社会效益。
| [1] |
杨旭旭, 靖洪文, 陈坤福, 等. 深部原岩应力对巷道围岩破裂范围的影响规律研究[J]. 采矿与安全工程学报, 2013, 30(4): 495-550. YANG Xuxu, JING Hongwen, CHEN Kunfu, et al. Study on influence law of in-situ stress in deep underground rocks on the size of failure zone in roadway[J]. Journal of Mining & Safety Engineering, 2013, 30(4): 495-550. (in Chinese) |
| [2] |
张雯, 曹平. 某铜矿二次应力场的监测与分析[J]. 南华大学学报(自然科学版), 2009, 23(1): 42-44. ZHANG Wen, CAO Ping. Monitoring and analysis of the secondary stress of copper mine[J]. Journal of University of South China (Science and Technology), 2009, 23(1): 42-44. (in Chinese) |
| [3] |
Wang S R, Li N, Li C L, et al. Mechanics Evolution Characteristics Analysis of Pressure-arch in Fully-mechanized Mining Field[J]. Journal of Engineering Science & Technology Review, 2014, 7(4): 40-45. |
| [4] |
徐文彬, 宋卫东, 万海文. 大阶段嗣后充填回采顺序及出矿控制技术研究[J]. 金属矿山, 2011(6): 13-15. XU Wenbin, SONG Weidong, WAN Haiwen. Study on mining sequence and ore-drawing control technique of high-stage backfill mining[J]. Metal Mine, 2011(6): 13-15. (in Chinese) |
| [5] |
Wang Y, Jing H, Zhang Q, et al. Prediction of collapse scope of deep-buried tunnels using pressure arch theory[J]. Mathematical Problems in Engineering, 2016, 2016: 1-10[2018-1-30]. http://dx.doi.org/10.1155/2016/2628174.
|
| [6] |
Sansone E C, Silva L A A D. Numerical modeling of the pressure arch in underground mines[J]. International Journal of Rock Mechanics & Mining Sciences, 1998, 35(4): 436. |
| [7] |
Wang P, Li H Q, Li Y, et al. Stability analysis of backfilling in subsiding area and optimization of the stopingsequence[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2013, 5(6): 478-485. DOI:10.1016/j.jrmge.2013.07.008 |
| [8] |
Liu Y Z, Wang Q H, Ye Y C, et al. Optimization of Stopestructure parameters in E'xi Iron Mine based on rock stress analysis[J]. Applied Mechanics & Materials, 2011, 66/67/68: 1434-1439. |
| [9] |
Wang W, Zhang H, Bian J. Research on the opportunity of construction method conversion in upper-soft and lower-hard stratum based on pressure arch theory[C]//International Congress and Exhibition "Sustainable Civil Infrastructures: Innovative Infrastructure Geotechnology". [S. l. ]: Springer, 2017: 8-16.
|
| [10] |
秦健春, 王新民. 充填法两步回采采场结构参数优化[J]. 矿冶工程, 2012, 32(4): 1-4. QIN Jianchun, WANG Xinmin. Stopestructure parameters optimization forbackfill by two-step stoping[J]. Mining and Metallurgical Engineering, 2012, 32(4): 1-4. (in Chinese) DOI:10.3969/j.issn.0253-6099.2012.04.001 |
| [11] |
Shabanimashcool M, Li C C. Numerical modelling of longwall mining and stability analysis of the gates in a coal mine[J]. International Journal ofRock Mechanics & Mining Sciences, 2012, 51(4): 24-34. |
| [12] |
杨玉学, 程宏, 杨天宝. 基于Flac3D数值模拟的阶段回采顺序研究[J]. 金属矿山, 2013, 446(8): 24-26. YANG Yuxue, CHENG Hong, YANG Tianbao. Study of stage stopingsequence based on Flac3D numerical simulation software[J]. Metal Mine, 2013, 446(8): 24-26. (in Chinese) DOI:10.3969/j.issn.1001-1250.2013.08.007 |
| [13] |
王李管, 任助理, 潘传鹏, 等. 基于混合整数规划法的采场回采顺序优化分析[J]. 中国有色金属学报, 2016, 26(1): 173-179. WANG Liguan, REN Zhuli, PAN Chuanpeng, et al. Optimization analysis of stope mining sequence based onmixed integer programming[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(1): 173-179. (in Chinese) |
| [14] |
叶义成, 施耀斌, 王其虎, 等. 缓倾斜多层矿床充填法开采围岩变形及回采顺序试验研究[J]. 采矿与安全工程学报, 2015, 32(3): 407-413. YE Yicheng, SHI Yaobin, WANG Qihu, et al. Experimental study of deformation of wall rock andstoping sequence in mining gently inclined andmultilayer deposits by backfill mining[J]. Journal of Mining & Safety Engineering, 2015, 32(3): 407-413. (in Chinese) |
| [15] |
Wu X, Tu Z. Research of the shape of pressure arch in layered rock mass based on the Protodyakonov's theory[C]//2017 7th International Conference on Manufacturing Science and Engineering (ICMSE 2017). [S. l. ]: ICMSE, 2017[2018-1-30]https://www.researchgate.net/publication/316901765_Research_of_the_Shape_of_Pressure_Arch_in_Layered_Rock_Mass_Based_on_the_Protodyakonov's_Theory. DOI: 10.2991/icmse-17.2017.45.
|
| [16] |
Shi R X, Ai C, Zhao W C, et al. The damage mechanics model of the wellbore surrounding rock based on fractal theory[J]. Applied Mechanics & Materials, 2013, 423/424/425/426: 1623-1626. |
| [17] |
王云飞, 李长洪. 不同开挖方式地下硐室压力拱的演变机理研究[J]. 矿业研究与开发, 2009, 29(3): 12-20. WANG Yunfei, LI Changhong. Research on evolution mechanics of pressure arch of underground cavern excavated in different ways[J]. Mining Research and Development, 2009, 29(3): 12-20. (in Chinese) |
| [18] |
马小虎, 李德武, 马为功. 纸坊隧道压力拱拱体的确定[J]. 甘肃科技, 2011, 27(6): 136-138. MA Xiaohu, LI Dewu, MA Weigong. Determination of pressure arch in Zhifang tunnels[J]. Gansu Science and Technology, 2011, 27(6): 136-138. (in Chinese) DOI:10.3969/j.issn.1000-0952.2011.06.049 |
| [19] |
Anwar K. A study on stress rock arch development around dual caverns[D]. Nanyang: Technological University, Singapore, 2003.
|
| [20] |
潘常甲. 新桥矿深部岩体力学性质分析及稳定性综合分级研究[D]. 长沙: 中南大学, 2009. PAN Changjia. Study on mechanical properties and stability classification of deep rock mass in XinqiaoMine[D]. Changsha: Central South University, 2009. (in Chinese) |
| [21] |
Song Y X. Calculation of surrounding rock pressure based on pressure arch theory[C]//5th International Conference on Advanced Materials and Computer Science (ICAMCS 2016)2016. [S. l. ]: Atlantis Press, 2016: 276-283.
|
| [22] |
PoulsenBA. Coal pillar load calculation by pressure arch theory and near field extraction ratio[J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47(7): 1158-1165. |
 2018, Vol. 41
2018, Vol. 41


