2. 重庆大学 能源与动力工程学院, 重庆 400044;
3. 武汉天和技术股份有限公司, 武汉 430077
2. College of Energy and Power Engineering, Chongqing University, Chongqing 400044, P. R. China;
3. Wuhan Tianhe Technology Co., Ltd., Wuhan 430077, P. R. China
中国是以煤炭为主要能源的国家,2017年燃煤火力发电量占全年总发电量的67%[1]。发电过程中煤炭燃烧产生的二氧化硫排放问题尤为引人关注,在一定的气象条件下产生复杂的化学反应,是形成雾霾和酸雨的重要前驱体。石灰石-石膏湿法烟气脱硫工艺应用最广[2],然而,循环浆液将持续富集来自烟气及脱硫剂中的重金属元素和氯离子,从而产生高浓度的脱硫废水,废水直接排放对环境产生负面影响。如采用常规工艺进行废水零排放处理,则高浓度氯离子的腐蚀性对设备材质要求很高,造价昂贵。使用喷嘴将脱硫废水雾化为液滴群并喷入空气预热器至电除尘器间的烟道内,利用高温烟气与常温废水的传热作用实现脱硫废水的零排放,有投资少、工艺流程短、去除重金属离子[3]、建设工期短、维护成本低等特点,被推荐为实现脱硫废水零排放的可行性技术。针对脱硫废水液滴群在烟气中蒸发与流动特性的优化是实现脱硫废水烟道蒸发零排放的关键。
目前,国内外对于脱硫废水烟道蒸发工艺的研究主要集中在以数值模拟的方式研究脱硫废水蒸发特性、流动特性两方面,同时,伴以一定的工程或实验数据作为参照。张子敬等[4]研究认为喷雾液滴群蒸发特性受到液滴加热升温(传热过程)和喷雾液滴群在烟气中的扩散(传质过程)两方面的共同作用。Strotos G等[5]建立了单个液滴在高温燃气中蒸发、运动过程的数学模型,获得了不同燃气温度和速度下液滴的蒸发规律。冉景煜等[6]对不同物性液滴在低温烟气环境中的运动,以及受热和蒸发过程中的传热传质特性进行了理论分析。李明波等[7]通过计算流体动力学软件Fluent,对空气预热器出口至电除尘器入口段烟道内的烟气流动情况进行了模拟。Laín等[8]的以拉格朗日湍流颗粒分散体模型的建立为基础,提出携带稀薄粒子的气流在一定条件下,假设粒子为球体,只考虑曳力和重力作用。Young等[9]应用离散多组分(DMC)燃料液滴模型对多组分燃料喷雾的蒸发进行了数值模拟。Pinto等[10]研究了双流体喷嘴的喷雾干燥,成功地预测了干燥时间和最终含水量随着初始液滴直径变化的趋势。晋银佳等[11]等提出深度过滤脱硫废水预处理工艺,将脱硫废水在雾化蒸发前进行固液深度分离预处理以解决硫废水中悬浮颗粒物堵塞问题。国内外学者已对液滴蒸发的机理进行了深入研究,重点考察烟气温度、速度、液滴直径、液滴速度对蒸发的影响,但是,不同雾化嘴角对脱硫废水蒸发的影响尚未有明确的解释,文中结合国内某燃煤电厂330 MW机组空气预热器至电除尘器间的烟道中喷雾蒸发实现脱硫废水零排放工程实践,数值模拟不同烟气负荷和不同喷雾锥角对脱硫废水喷雾蒸发流动特性的影响。
1 方法与模型脱硫废水在烟道中喷雾蒸发属于典型的气液两相流流动,在数值模拟中以空气为连续相,以喷雾液滴为离散相,主要考虑连续相和离散相之间的相间运动和相互作用。首先,建立烟道的物理模型,根据连续相和离散相方程,以确定的边界条件进行相应数值模拟计算。
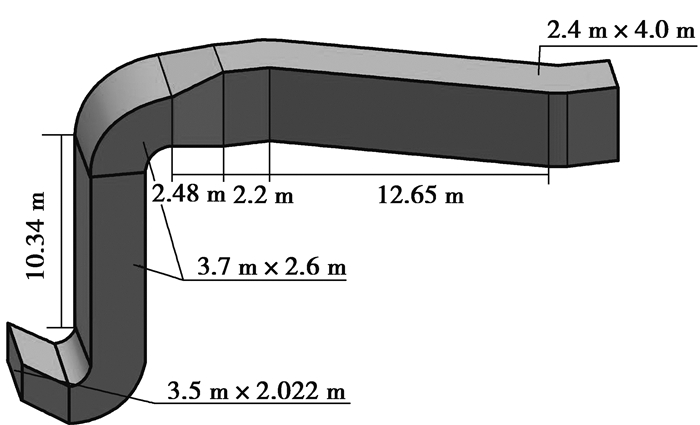
1.1 物理模型图 1所示为空气预热器与电除尘器之间烟道和尺寸的物理模型。烟道分为入口段、下弯头、竖直段烟道、上弯头、异型弯头和水平烟道6个部分。采用ANSA软件对烟道几何模型进行网格划分,该烟道模型结构简单,流场结构均匀,在计算速度上采用有明显优势的全六面体网格,生成总网格数为200万。经检验,该模型网格EquiSize Skew值在0~0.4之间的网格数占98.09%,网格划分质量较高。
|
图 1 烟道结构的物理模型 Figure 1 The physical model of flue structure |
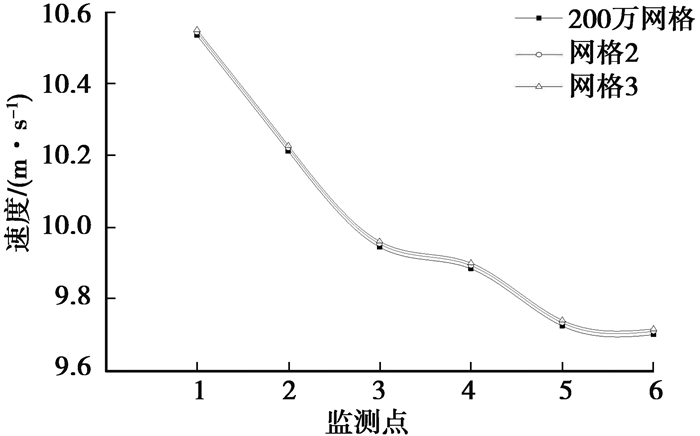
采用网格数分别为200万和300万和400万的网格进行无关化验证,对竖直段烟道内的6个点进行速度监测,3种网格计算结果相差不大,为了节省计算资源,选择网格数量约为200万的网格进行模拟,如图 2所示。
|
图 2 不同网格数量的监测点速度 Figure 2 Monitoring point speeds with different grid numbers |
在气液两相流动中,尽管控制方程独立,两相却是相互耦合的。液滴作为质量源、动量源和能量源被引入到气相方程中,并通过这些源项影响气相流场,气相流场又反过来通过其速度场、温度场、压力场等来影响液滴的本身状态。下列方程为气相控制方程,其表达式分别如下。
连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}} \right) = {S_m}。$ | (1) |
动量方程:
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}{\mathit{\boldsymbol{\tau }}_{ji}} + {S_{{\rm{mon}}}}。$ | (2) |
能量方程:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho E{u_j}} \right) = \rho {g_j}{u_j} - \frac{{\partial p{u_j}}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}{\mathit{\boldsymbol{\tau }}_{ji}}{u_i} + \\ \;\;\;\;\;\;\;\frac{\partial }{{\partial {x_j}}}\left( {\lambda \frac{{\partial T}}{{\partial {x_j}}}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\sum\limits_{s = 1}^n {{h_s}\rho D\frac{{\partial {Y_s}}}{{\partial {x_j}}}} } \right) + {S_{{\rm{en}}}}。\end{array} $ | (3) |
气相组分方程:
| $ \frac{\partial }{{\partial t}}\left( {\rho {Y_s}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}{Y_s}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {D\rho \frac{{\partial {Y_s}}}{{\partial {x_j}}}} \right) + {{\dot \omega }_S} + {S_{{Y_s}}}。$ | (4) |
式中:ρ、u、T、λ分别表示气相的密度、速度、温度和热传导系数;p和τji为压力和剪应力张量;
对于源项,其表达式如下。
1) 质量守恒方程中的源项
质量源项的来源是单位体积重所有液滴蒸发使气相质量的增加率:
| $ {S_{\rm{m}}} = - \sum\limits_k {{n_k}{{\dot m}_k}} , $ | (5) |
其中,
2) 动量守恒方程中作用的源项
液滴对气相动量的贡献有2方面的因素,一是液滴对气相的反作用力Sdi,二是液滴蒸发质量带给气相的动量Sdm,即Smon=Sdi+Sdm。
单位体积中所有液滴反作用力使气体动量在i方向的增加率为
| $ {S_{{\rm{d}}i}} = - \sum\limits_k {{\rho _k}{A_k}{f_k}\left( {{u_i} - {u_{ki}}} \right)} , $ | (6) |
单位体积中所有液滴蒸发带给气相的动量为
| $ {S_{{\rm{dm}}}} = - {S_{\rm{m}}}{u_i}, $ | (7) |
式中,ui和uki为气相和k液滴在i方向的速度分量。
3) 能量守恒方程中的源项
液滴作用与气相的贡献有4个:液滴向气相对流传热Seh,液滴的反作用力对气相做功Sed,液滴蒸发物质带给气相的焓Sem和作用于气相的液滴相变热Seq,则能量源项为Sen=Seh+Sed+Sem+Seq。
单位体积中所有液滴对气相的对流传热为
| $ {S_{{\rm{eh}}}} = - \sum\limits_k {{\rho _k}{B_k}\left( {T - {T_k}} \right)} , $ | (8) |
单位体积中所有液滴的反作用力对气相做功为
| $ {S_{{\rm{ed}}}} = - \sum\limits_k {{\rho _k}{A_k}\left( {{u} - {u_{ki}}} \right){u_{ki}}} , $ | (9) |
单位体积中所有液滴蒸发物质带给气相的焓为
| $ {S_{{\rm{em}}}} = - \sum\limits_k {{n_k}{{\dot m}_k}\left( {e + \frac{{u_i^2}}{2}} \right)} , $ | (10) |
式中,e是单位质量气相的内能。
单位体积中所有液滴相变分配给气相的相变热为
| $ {S_{{\rm{eq}}}} = - \sum\limits_k {{n_k}{{\dot m}_k}\left( {1 - {\beta _k}} \right)Q} , $ | (11) |
式中:Q是单位质量相变热;ρk为Q分配给k液滴的分数。
4) 组分质量守恒中的源项
液滴蒸发向气相传质,使气相组分s的质量分数增加。设单位体积内所有液滴蒸发转变为气相组分s的质量分数为αs,则单位体积内所有液滴蒸发贡献给组分的质量分数为
| $ {S_{Ys}} = - \sum\limits_k {{\alpha _s}{n_k}{{\dot m}_k}} 。$ | (12) |
在离散相求解过程中,拉格朗日颗粒随机轨道模型应用较为广泛,该模型计算简单,能较好地追踪并记录颗粒的运动轨迹及状态,同时,考虑了气相湍流脉动与离散相颗粒的耦合作用。
颗粒运动方程为
| $ {m_p}\frac{{{\rm{d}}{\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{p}}}}}{{{\rm{d}}t}} = \sum {{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{p}}}} + {m_p}g。$ | (13) |
仅考虑曳力:
| $ {F_D} = \frac{{18\mu }}{{{\rho _p}d_p^2}}\frac{{{C_D}\mathit{Re}}}{{24}}, $ | (14) |
| $ \mathit{Re} = \frac{{\rho {d_p}\left| {{\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{p}}} - \mathit{\boldsymbol{u}}} \right|}}{\mu }, $ | (15) |
其中:CD为阻力系数;μ为烟气动力粘度;ρp为颗粒密度;dp为颗粒直径,Re为相对雷诺数。
由于喷雾液滴温度(约300 K)低于烟气温度(约400 K),液滴群喷入烟气后将吸收烟气热量蒸发为水蒸气。当液滴温度低于其沸点时,液滴的相变主要表现为蒸发过程,液滴蒸发模型[12]表达式为
| $ {\mathit{m}_{\rm{p}}}\left( {t + \Delta t} \right) = {m_p}\left( t \right) - {N_i}{A_{\rm{p}}}{M_{w,i}}{\Delta _t}, $ | (16) |
式中,mp(t+Δt)表示液滴相变后的质量,mp(t)表示相变前质量;Ni表示液滴的单位面积蒸发率;Ap为液滴的表面积;Mw.i为蒸发组分的分子量;Δt为时间步长。
当液滴温度高于其沸点时,液滴的相变主要表现为沸腾过程,液滴沸腾模型为
| $ \frac{{{\rm{d}}\left( {{d_{\rm{p}}}} \right)}}{{{\rm{d}}t}} = \frac{{4{k_\infty }}}{{{\rho _{\rm{p}}}{c_{{\rm{p,}}\infty }}{d_{\rm{p}}}}}\left( {1 + 0.23\sqrt {\mathit{R}{\mathit{e}_d}} } \right)\ln \left[ {1 + \frac{{{c_{{\rm{p}},\infty }}\left( {{T_\infty } - {T_{\rm{p}}}} \right)}}{{{h_{fg}}}}} \right], $ | (17) |
式中:cp, ∞表示气体定压比热容;ρp表示液滴密度;k∞表示气相导热率;hfg为气化潜热。
1.3 边界条件选取330 MW机组在3种不同烟气负荷下,空气预热器出口截面的烟气作为气相研究对象,其包含H2O,CO2,O2,SO2及N25种组分,采用组分输运模型进行混合物组分模拟。选取常温下的电厂脱硫废水液滴群为液相研究对象,连续相和离散相两相流场各参数如表 1所示。
| 表 1 气液两相流场参数 Table 1 Parameters of gas-liquid two-phase flow field |
将喷嘴放置于下弯头上方竖直段烟道3 m处,在单个烟道中放置3个喷嘴,其位置为烟道长边的四分点位置和短边的中心位置。
2 结果与分析 2.1 烟气负荷对液滴群蒸发及运动过程的影响脱硫废水在锅炉尾部烟道中的雾化及流动、蒸发过程可分为初始阶段和稳态阶段。初始阶段,常温液滴群作为吸热蒸发的分布热汇,充分吸收烟气流的余热,所吸收的热量大部分用于液滴群温度的升高,同时,在烟气速度的影响下,该阶段的液滴群速度不断增大;在很短时间内,雾化液滴群即达到稳态阶段,此时,液滴群被烟气加热到稳定值,吸收的所有热量都用于液滴群蒸发,液滴群速度与来流烟气速度一致。
液滴群的蒸发效果主要由以下参数共同决定:气相温度、传输特性、液相温度、运动速度以及气液两相的传热、传递效率,分别选取330 MW机组50%、75%、100%烟气负荷工况下,3种不同烟温(120.3、125.1、128.9 ℃)及烟速(9.19、11.56、14.64 m/s)的气相条件对脱硫废水蒸发及流动特性的影响作定量分析,并结合传热传质理论加以解释。
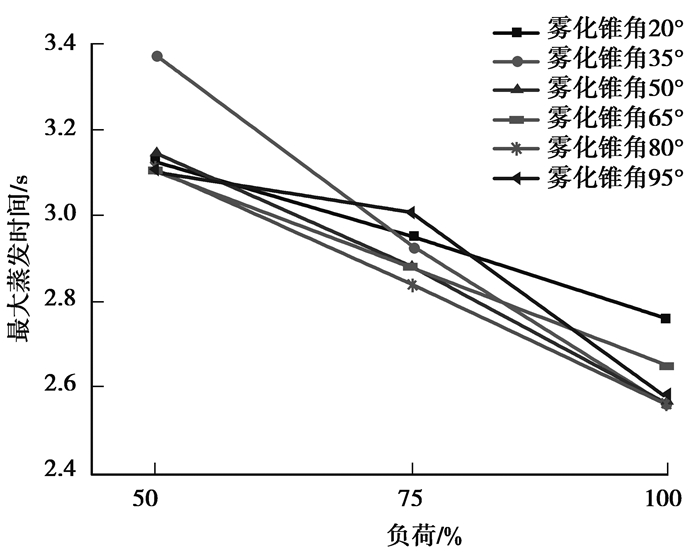
图 3显示了50%、75%、100% 3种不同烟气负荷下,以不同的雾化锥角进行喷雾,运动液滴最大蒸发时间T的模拟结果,T值随烟气负荷的增加呈现近乎相同的线性下降趋势。随着负荷的增加烟气量增加,烟道烟气温度降低减少,蒸发时间减少,其中,50%、75%及100%烟气负荷工况运动液滴最大蒸发时间T分别在3.07~3.36 s、2.85~3.04 s和2.57~2.80 s范围内。
|
图 3 液滴群在不同烟气负荷下的蒸发特性 Figure 3 Evaporation characteristics of liquid droplets under different flue gas loads |
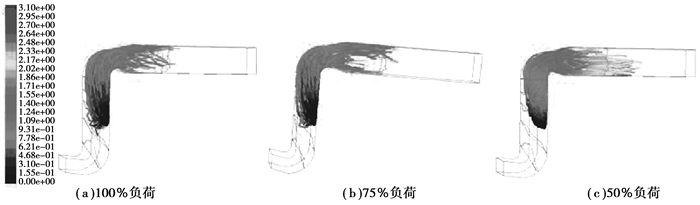
选取喷嘴雾化锥角65°配置下的各烟气负荷颗粒运动轨迹,如图 4所示。
|
图 4 颗粒在不同负荷下的运动轨迹图 Figure 4 Particle trajectories at different boiler load |
液滴群颗粒皆能蒸发完全,100%烟气负荷对应的最大蒸发时间最短,50%烟气负荷对应的最大蒸发时间最长,由此可见,对于相同粒径的液滴,气体环境温度越高、烟气速度越快,液滴群的汽化速率越高、蒸发效果越好。其中,由于100%负荷下烟气速度相较于75%和50%负荷时更快,则脱硫废水颗粒衰减后的速度仍然较快,若烟道长度不足,仍有蒸发不完全的可能性,从图中可看出,烟气速度的变化对液滴最大完全蒸发时间的影响较小,故在单烟道结构中,烟气温度对蒸发效果起主导作用。若烟气温度升高,则气液两相的温差增大,气体环境向液滴群的传热增强,从而使液滴表面蒸发及传质扩散速率不断增大,因此,液滴温度持续升高,其到达临界蒸发温度所需时间变短,液滴自喷入烟道至完全蒸发的停留时间随烟气温度升高而逐渐减少。
2.2 雾化锥角对液滴群蒸发及运动过程的影响为定量分析雾化锥角对雾化液滴群流动特性的影响,定义被烟道壁面捕捉的液滴数量占液滴颗粒总数比为A0。A0值可反映出脱硫废水喷雾蒸发结晶后,在烟道内壁积灰的可能性大小。
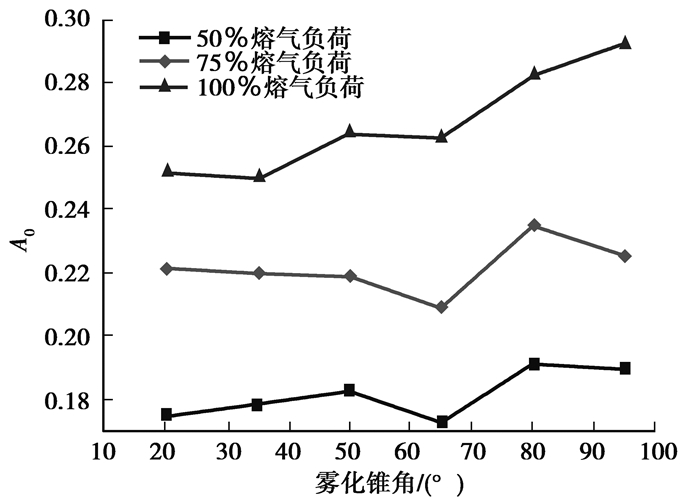
图 5显示了在20°、35°、50°、65°、80°、95° 6种不同雾化锥角下在单烟道壁面被捕捉的液滴数量分数的模拟结果,A0值随雾化锥角的变化呈现近乎相同的先平稳下降、后明显上升趋势。图 5表明:在雾化锥角由20°至50°增加的过程中,A0值变化相对平稳,由于雾化角过小,液滴蒸发速度较慢,易撞击顶部水平烟道;当雾化锥角增加至65°,烟道捕捉的液滴数达到最小值,说明65°雾化锥角在烟道内壁积灰可能性最小;雾化锥角由65°至95°继续增大的过程中,A0值呈明显增加趋势,此时,由于雾化角过大液滴易撞击竖直烟道,但雾化锥角大于90°后,增加速率有所放缓,且有下降趋势,随着雾化角的增大,液滴蒸发速度变快,液滴碰壁的可能性变小。当喷嘴雾化锥角过小时,相同工况下液滴蒸发较慢。当液滴进入水平烟道时,由于液滴的直径相对较大,随流能力也就越弱,液滴越撞击水平烟道形成积灰。当喷嘴雾化锥角过大时,液滴容易直接撞击竖直烟道形成积灰。因此,存在1个最佳的雾化锥角使液滴的碰壁数量最小,经过验证当雾化锥角为65°时撞击烟道的液滴数量最小。
|
图 5 液滴群在不同雾化锥角下的流动特性 Figure 5 Flow characteristics of droplets group under different cone angles of atomization |
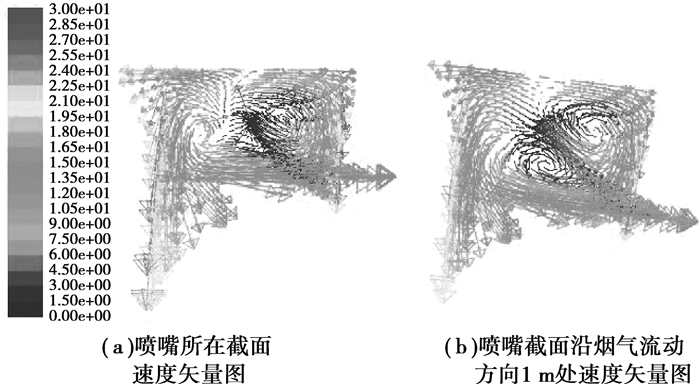
单烟道结构75%烟气负荷工况下,最佳雾化锥角65°时,对于脱硫废水蒸发及流动特性的定量及烟道截面速度矢量图,如图 6所示。由图 6可知,在喷雾蒸发的初始阶段,传质扩散及蒸发速率较快,喷雾对烟气的剪切卷吸形成了一个较大的不规则的涡。由于烟道内侧的烟气体积流量较大,喷嘴截面沿烟气流动方向1 m处烟气以较快的速度冲入对墙,造成其上部有较大压强差而形成回流,故越靠近烟道内侧,涡的形态越大,有利于促进喷嘴区的局部液滴群不断向其他区域扩散。随着蒸发及传质扩散的进一步均匀化,喷雾蒸发进入稳态阶段,烟道通流截面涡增大,截面涡的形态逐渐规则化,速度矢量场趋于稳定。
|
图 6 喷雾液滴沿烟气流动方向的流动特性 Figure 6 Flow characteristics of spray droplets in the direction of flue gas flow |
1) 50%、75%、100% 3种烟气负荷工况下,在单烟道壁面被捕捉的液滴数量分数随雾化锥角的增加皆呈现先平稳下降、后明显上升趋势。
2) 在20°、35°、50°、65°、80°、95° 6种不同雾化锥角下运动液滴最大蒸发时间值随烟气负荷的增加呈现近乎相同的线性下降趋势。在最佳喷嘴雾化锥角65°配置下,对于相同粒径的液滴,气体环境温度越高、烟气速度越快,液滴群的汽化速率越高、蒸发效果越好。其中,烟气速度的变化对液滴最大完全蒸发时间的影响较小,烟气温度对蒸发效果起主导作用。脱硫废水喷雾后形成的液滴群可在烟道中完全蒸发。
3) 最佳雾化锥角配置下的速度矢量图显示,越靠近烟道内侧,涡的尺寸越大,有利于促进喷嘴区的局部液滴群不断向其他区域扩散;喷雾蒸发初始阶段的传质扩散及蒸发速率较快,速度矢量图呈现出一个较大的不规则的涡形态;喷雾蒸发稳态阶段烟道通流截面涡增大、形态逐渐规则化,速度矢量场趋于稳定。
| [1] |
中华人民共和国国家统计局. 中华人民共和国2016年国民经济和社会发展统计公报[J]. 中国统计, 2017(3): 4-8. National Bureau Statistics of China. Statistical communique of the People's Republic of China on the 2016 national economic and social development[J]. China Statistics, 2017(3): 4-8. (in Chinese) |
| [2] |
吴怡卫. 石灰石-石膏湿法烟气脱硫废水处理的研究[J]. 中国电力, 2006, 39(4): 75-78. WU Yiwei. Study on the wastewater treatment in limestone-gypsum wet FGD process[J]. Electric Power, 2006, 39(4): 75-78. (in Chinese) |
| [3] |
Liang Z, Zhang L, Yang Z, et al. Evaporation and crystallization of a droplet of desulfurization wastewater from a coal-fired power plant[J]. Applied Thermal Engineering, 2017, 119: 52-62. DOI:10.1016/j.applthermaleng.2017.02.113 |
| [4] |
张子敬, 汪建文, 高艺, 等. 燃煤电厂脱硫废水烟气蒸发特性流场模拟[J]. 煤炭学报, 2015, 40(3): 678-683. ZHANG Zijing, WANG Jianwen, GAO Yi, et al. Flow field simulation of smoke and gas evaporation characteristics of desulfurization wastewater in coal-fired power plant[J]. Journal of China Coal Society, 2015, 40(3): 678-683. (in Chinese) |
| [5] |
Strotos G, Malgarinos I, Nikolopoulos N, et al. Predicting the evaporation rate of stationary droplets with the VOF methodology for a wide range of ambient temperature conditions[J]. International Journal of Thermal Sciences, 2016, 109: 253-262. DOI:10.1016/j.ijthermalsci.2016.06.022 |
| [6] |
冉景煜, 张志荣. 不同物性液滴在低温烟气中的蒸发特性数值研究[J]. 中国电机工程学报, 2010, 30(26): 62-68. RAN Jingyu, ZHANG Zhirong. Evaporation characteristics of different substance droplet in low temperature flue gas[J]. Proceedings of the CSEE, 2010, 30(26): 62-68. (in Chinese) |
| [7] |
李明波, 范玺, 孙克勤. 利用烟道气处理火电厂WFGD废水的技术应用[J]. 电力科技与环保, 2010, 26(2): 53-55. LI Mingbo, FAN Xi, SUN Keqin. Technique application on WFGD wastewater treatment using flue gas in power piants[J]. Electric power technology and environmental protection, 2010, 26(2): 53-55. (in Chinese) DOI:10.3969/j.issn.1674-8069.2010.02.017 |
| [8] |
Laín S, Grillo C A. Evaluation of lagrangian particle dispersion models in turbulent flows[J]. Chemical Engineering Communications, 2007, 195(3): 189-208. |
| [9] |
Ra Y, Reitz R D. A vaporization model for discrete multi-component fuel sprays[J]. International Journal of Multiphase Flow, 2009, 35(2): 101-117. DOI:10.1016/j.ijmultiphaseflow.2008.10.006 |
| [10] |
Pinto M, Kemp I, Bermingham S, et al. Development of an axisymmetric population balance model for spray drying and validation against experimental data and CFD simulations[J]. Chemical Engineering Research & Design, 2014, 92(4): 619-634. |
| [11] |
晋银佳, 王帅, 姬海宏, 等. 深度过滤-烟道蒸发处理脱硫废水的数值模拟[J]. 中国电力, 2016, 49(12): 174-179. JIN Yinjia, WANG Shuai, JI Haihong, et al. Numerical simulation of desulfurization wastewater treatment with in-depth filtration-flue evaporation process[J]. Electric Power, 2016, 49(12): 174-179. (in Chinese) DOI:10.11930/j.issn.1004-9649.2016.12.174.06 |
| [12] |
Borodulin V Y, Letushko V N, Nizovtsev M I, et al. Determination of parameters of heat and mass transfer in evaporating drops[J]. International Journal of Heat & Mass Transfer, 2017, 109: 609-618. |
 2018, Vol. 41
2018, Vol. 41

