2. 重庆大学 光电工程学院, 重庆 400044;
3. 中国科学院 重庆绿色智能技术研究院, 重庆 400714
2. College of Optoelectronic Engineering, Chongqing University, Chongqing 400044, P. R. China;
3. Chongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences, Chongqing 400714, P. R. China
液体表面流速是确定流体运动特性的基本参量之一[1]。目前,在水动力实验中所采用的流速测量方法根据测量点的数目不同可以划分为两类[2]。一类是单点式测量,例如声学多普勒流速剖面仪和激光多普勒测速仪。这类方法适于对流场进行单点测量,多数需要接触或进入流场,而且实验设备价格往往较为昂贵[3-4]。另一类方法是多点式测量,例如粒子跟踪测速技术(PTV, paticle tracking velocimetry)、激光散斑全场测速技术(LSV, laser speckle velocimetry)和粒子图像测速技术(PIV, particle image relocimetry)。这类方法能对流场进行多点非接触测量,操作简单[5-6]。PTV、LSV和PIV技术的主要区别在于示踪粒子的浓度不同。LSV技术要求粒子浓度极高,这对流场干扰较大[7]。PTV由于粒子浓度极低,使得PTV技术可提取的流场速度信息较少,从而限制了对流场细微结构的研究[8]。与前2种方法不同的是PIV技术选择的粒子浓度适中,不仅保证了流场流速信息,而且减小了示踪粒子浓度对流场的干扰[9-10]。PIV技术不仅克服了接触式单点测量设备的局限性,能够进行平面二维流场的测试,同时具有较高精度,是一种具有发展前景的无扰动流场测量技术[11]。因此,研究提出的方法采用了PIV技术思想。
互相关法和光流法都是传统PIV测速系统获取流速矢量的主要方法[12]。互相关法的基本原理是从2幅独立拍摄的图像中,通过一个已知的时间间隔和2幅图像中相应的取样窗口相互关系,获得瞬时平面速度分布[13]。2010年,Wang等构建了针对河工模型表面流速测量的PIV测速系统,选用了激光光源为系统提供照明。他们的系统采用互相关法来获取流速矢量。由于互相关法概念简单,因此易于实现。但互相关算法会因为种种原因得到一定数量的错误矢量,如示踪粒子偏离聚焦平面和噪声干扰等原因都将在矢量场的局部得到错误结果[14]。另一方面,光流场反映了图像上每一点灰度的变化趋势,可看成是带灰度的像素点在图像平面上运动而产生的瞬时速度场,也是一种对真实运动场的近似估计。2014年,Shi等人提出了一种基于光流法的PIV测速算法。大量实验结果表明他们提出的算法对于处理PIV图像具有较好的可靠性[15-16]。但是应用光流法有3个前提:1)亮度恒定,像素被逐帧跟踪时其亮度不发生变化;2)图像的运动随时间变化比较缓慢;3)一个场景中同一表面上邻近的点具有相似的运动[17]。而在实际应用场景中,很多时候亮度是不恒定的,不满足光流法的前提,从而降低了测速精度。此外,光流法还采用了迭代的方法,造成计算复杂耗时。
综上所述,现有的表面流速测量方法存在的问题有以下几个方面:1)对视频采集设备角度要求垂直于流速表面,应对外界光照影响的灵活性不足;2)多路数据分析速度慢,测量精度不够高。3)大多数流场测速系统使用的示踪粒子成本较高。为了解决以上问题,利用二值化局部特征进行匹配的方法来获取流速矢量,且支持视角自由,即视频采集设备的主光轴与流场表面可以成任意角度。此外,系统还支持任意类型的示踪粒子、照明光源和任意数目的视频采集设备。
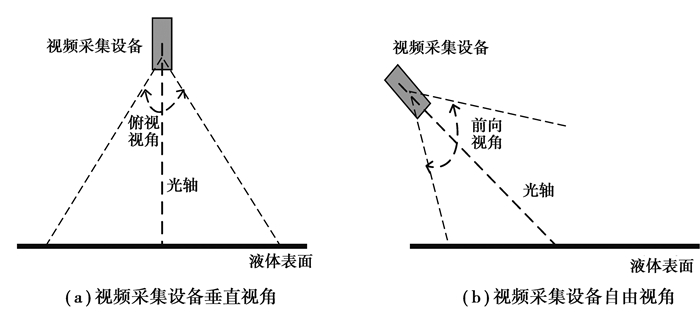
1 测量原理 1.1 自由视角与算法流程大多数PIV测速系统都要求视频采集设备光轴垂直于流场表面,如图 1(a)[15]。通过这种方法获取到的图像无畸变,算法难度小,但每次测量之前都需要对视频采集设备进行手工校正,测量过程繁琐。而且容易受到光照影响。针对此问题,笔者提出了图 1(b)所示的视频采集设备视角自由的方法。通过这种方法获取到的图像是前向视角图像,不需要每次测量前都对视频采集设备进行角度校正,使用简单方便,且视角范围广。在该系统中,视频采集设备角度和架设位置可自由选择,这样不仅使测量区域的选择更加灵活,而且可通过改变视频采集设备的朝向,降低阳光、灯光照射产生的反光影响,提高系统对于光照变化的适应能力。
|
图 1 视频采集设备视角图 Figure 1 Views of video capture devices |
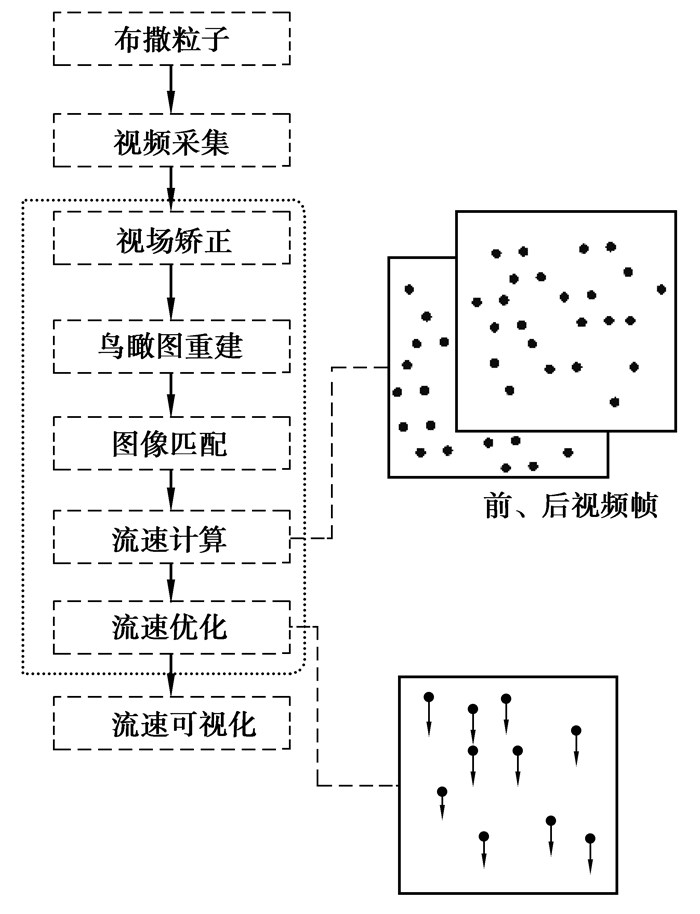
研究的算法流程主要包含流速测量和流速分析2个模块,如图 2所示。流速测量模块主要负责布撒粒子、视场矫正、鸟瞰图重建、图像匹配、流速计算、流速优化和流速可视化等过程。流速分析模块完成流速数据的后处理,具体功能包含导出流速数据、导出流速图片、合成动画等。
|
图 2 算法流程图 Figure 2 Algorithm flowchart |
在表面流场的测量中,布撒示踪粒子是一个重要的环节。而目前的测量方法中,示踪粒子都是采用定制的标准圆形粒子,且回收困难,这就不可避免地造成了测量成本高的问题。在提出的新方法中,对于示踪粒子的形状和类型没有特定的限制,故可以使用碎纸屑作为示踪粒子,几乎没有成本。而且碎纸屑示踪粒子分布密,获得的信息量大,故而相对于传统的示踪粒子,测量更加准确。除测量成本和测量精度上的主要优势以外,碎纸屑相比于传统示踪粒子更容易分解,对环境更加友好。
1.2.2 视场矫正与鸟瞰图重建由于采用了视频采集设备视角自由的流场测量方式,摄像机与被测量区域不是正摄关系,对于表面流场的测量非常不利。地面上的一个矩形区域,在鸟瞰图中仍然是一个矩形区域,而在自由视角形成的前向视角图中类似于梯形。鸟瞰图能很好地保留图像的线性和平行性特征,因此在算法设计中需要将前向视角图转换为鸟瞰图以方便流速测量。具体方法是:1)在视频帧里选取4个点。2)提取这个4个点的像素坐标。3)获取这4个点对应的流场模型中的模型坐标。4)根据这4个坐标点之间的对应关系,计算出透视变换矩阵。
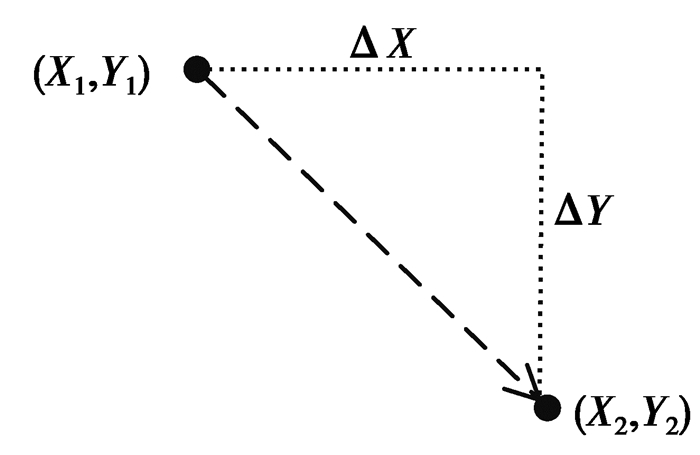
1.2.3 流速矢量的计算如图 3所示,黑色实心圆点表示特征点。同一特征点在t1时刻的位置为(X1,Y1),在t2时刻的位置为(X2,Y2)。
|
图 3 特征点位移示意图 Figure 3 Displacements of feature points |
根据速度、时间、路程的相关关系,可以得到公式(1)、(2)。
| $ {V_x} = \mathop {\lim }\limits_{t2 \to t1} \frac{{{X_2} - {X_1}}}{{{t_2} - {t_1}}} = \frac{{\Delta X}}{{\Delta t}}, $ | (1) |
| $ {V_y} = \mathop {\lim }\limits_{t2 \to t1} \frac{{{Y_2} - {Y_1}}}{{{t_2} - {t_1}}} = \frac{{\Delta Y}}{{\Delta t}}, $ | (2) |
其中:Vx、Vy分别表示特征点沿X方向与沿Y方向的平均速度;Δt为测量的时间间隔;ΔX、ΔY分别为时间间隔Δt时,特征点沿X方向与沿Y方向移动的距离。当Δt足够小时,就可以用Vx、Vy来表示流场的瞬时速度。由于示踪粒子的不均匀照明等因素,可能会发生多帧图像噪声,最终导致示踪粒子的错误识别和误匹配。因此,需要对原始流速数据进行进一步优化。
1.2.4 二值化局部特征匹配图像特征是图像匹配的一个重要内容。图像特征根据描述范围的不同可分为全局特征和局部特征。与全局特征相比,局部特征更适用于自由粒子的匹配,搜索能力更强。在测速过程中,在测量区域中产生具有一定尺寸的均匀网格。然后提取网格中心点作为局部特征点。由于二值化描述符具有加快特征匹配、减小存储数据量的优点,因此将二值化引入到算法中。
2016年,Li等人提出了针对原数据的PIMR(parallel and integrated matching for rawdata)匹配方法,直接以图像传感器输出的原数据代替数字图像作为分析对象,采用并行和集成的框架来加速整个图像匹配的算法。实验表明,该PIMR匹配方法对光照变化、图像模糊等都具有良好的鲁棒性。而且相比于BRIEF(Binary robust independent element feature)、ORB(Oriented brief)、BRISK(Binary robust invariant scalable keypoints)和FREAK(fast retina keypoint),PIMR耗时显著降低[18-19]。因此将PIMR匹配算法引入到了研究方法中,利用图像匹配的方法对图 3中ΔX和ΔY 2个参数进行求解。
当处理帧匹配时,添加方向给特征点。对于任意一个特征点p来说,定义p的邻域像素的矩为
| $ {\mathit{\pmb{m}}_{pq}} = \sum\nolimits_{x,y} {{x^p}{y^{pq}}I\left( {x,y} \right)} , $ | (3) |
| $ C = \left( {\frac{{{m_{10}}}}{{{m_{00}}}},\frac{{{m_{01}}}}{{{m_{00}}}}} \right), $ | (4) |
其中,p和q被设置为0或1,x和y是像素坐标。角点中心O到质心C的矢量OC即为图像块的方向矢量,方向角θ计算公式如下所示
| $ \theta = a\tan 2\left( {{m_{01}},{m_{10}}} \right)。$ | (5) |
根据上式,可得到具有方向的特征点。然后可以计算特征点的描述符。考虑一个平滑的图像块Q。τ表示描述符的每一位,定义如下
| $ \tau \left( {Q;a,b} \right): = \left( \begin{array}{l} 1,Q\left( a \right) < Q\left( b \right);\\ 0,Q\left( a \right) \ge Q\left( b \right); \end{array} \right., $ | (6) |
| $ \mathit{\pmb{S}} = \left( \begin{array}{l} {a_1}, \cdot \cdot \cdot ,{a_n}\\ {b_1}, \cdot \cdot \cdot ,{b_n} \end{array} \right), $ | (7) |
| $ \mathit{\pmb{S}} = {\mathit{\pmb{R}}_\theta }\mathit{\pmb{S}}, $ | (8) |
其中,Q(a)和Q(b)分别表示平滑后的图像块Q在点a和点b处的灰度值。测试对(A,B)定义为矩阵S,如公式(7)所示,Rθ为旋转矩阵。通过对旋转后的图像块上的测试对比灰度比较可得有向BRIEF描述符。对于特征匹配的部分,首先通过暴力匹配在待匹配数据上寻找特征点的k个最近邻点。然后采用类似SIFT(scale invariant feature transform)的方式根据显著性剔除误匹配对。此外,描述符之间的相似性是通过汉明距离来表征的,也可以通过逐位异或的方法来快速计算。
2 实验 2.1 实验设置河工模型试验对于大型水利工程建设、河道治理实践、河流开发利用、河流生态保护以及河口海岸治理与开发都具有重要意义[11]。作者将系统应用于河工模型试验,针对具体的河工模型进行了表面流速测试。研究所提出的方法在测试中均采用碎纸屑作为示踪粒子,利用自然光进行照明,几乎零成本且易操作。视频采集设备采用的是海康威视(Hikvision)DS-2CD3410FD-IW摄像机。该摄像机的分辨率为1 920×1 080,帧率为25~30 fps。
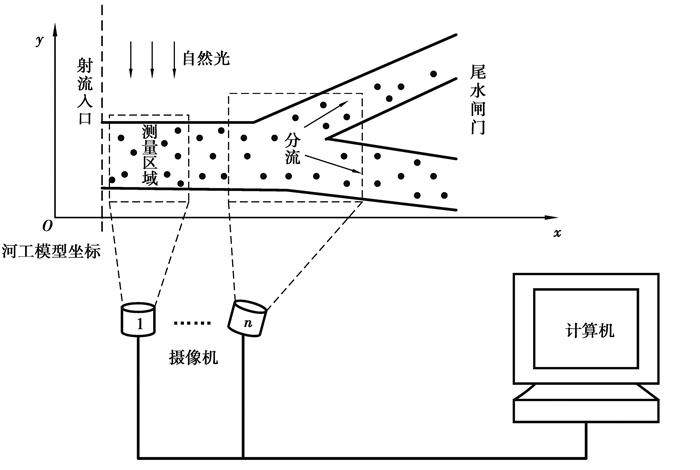
2.2 实验方法和结果如图 4所示,摄像机以任意角度、任意高度分散固定在河工模型上方。测试开始前,将所要测量的河工模型地图数据载入软件系统,并跟据所要测试的流段选择需要开启的摄像机以及对视场和采样时间等进行设置。测量时,首先使用碎纸机将废弃纸张绞碎,将碎纸屑均匀地洒在流场上游。这些碎纸屑跟随流体运动,以碎纸屑速度代表其所在流场内响应位置处流体的运动速度。然后开启软件上的视频采集按钮,开始采集视频。视频采集完成之后,导出流速数据。最后,将地图和流速数据加载到流速分析模块中,完成流场流速的可视化。
|
图 4 河工模型实验 Figure 4 Schematic diagram of measurement installation |
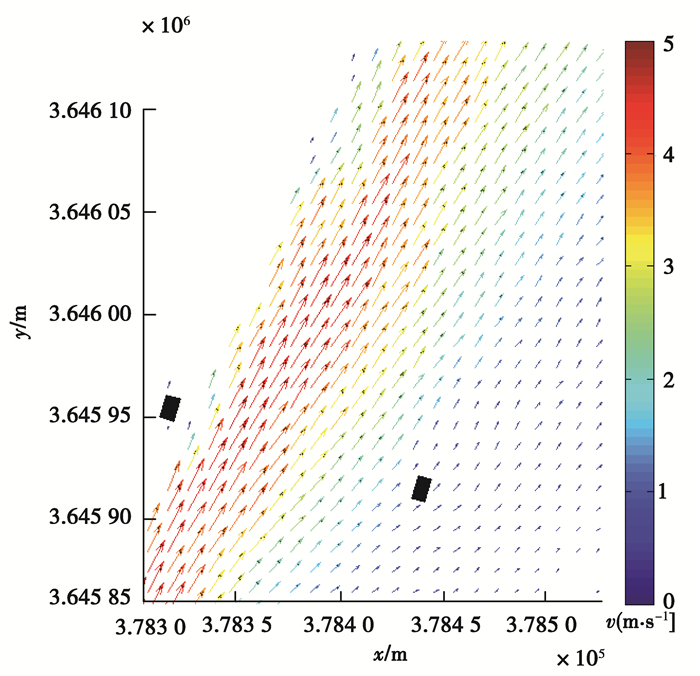
图 5是放大后的局部流速矢量图。内部的黑色矩形表示河工模型中的桥墩断面,横、纵坐标显示的是河工模型的真实尺寸,箭头表示测量点的流速矢量,箭头长度表示流速的大小,箭头指向表示流速的方向,箭头颜色变化表征流速大小。为了评估研究系统的精度,在温度为17 ℃,相对湿度为66%的测试环境条件下,对范围为1.7 m×2.5 m的流场进行表面流速测量,在不同参考值下的绝对误差如图 6所示。
|
图 5 流速可视化 Figure 5 Velocity visualization |
|
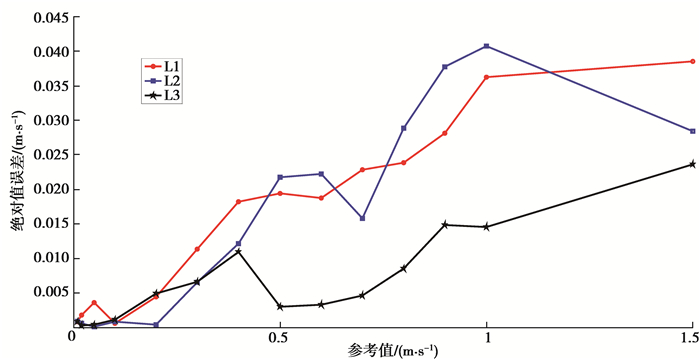
图 6 不同参考值下的绝对误差 Figure 6 Absolute error with different reference values |
曲线L1表示对流场内425个测试点的测量平均值与参考值之差的绝对值(绝对误差),L2与L3为系统随机选取的2个单一测试点的测量值与参考值之差的绝对值。通过对整体流速测量结果与单个测量点测量结果的统计分析可知,当流速在0.01~0.05 m/s范围内时,系统测量精度达到10%,当流速在0.1~1.5 m/s范围内时,系统测量精度达到5%。通过对全流场范围内流速测量方向结果的统计分析可知,0~1.5 m/s范围内,流速测量角度偏差均小于5°。
在处理速度方面,对于1 080 P视频的分析速度可为112~130 fps,比光流法的速度有明显提升。测试平台采用标准电压I7处理器、8 Gb内存。
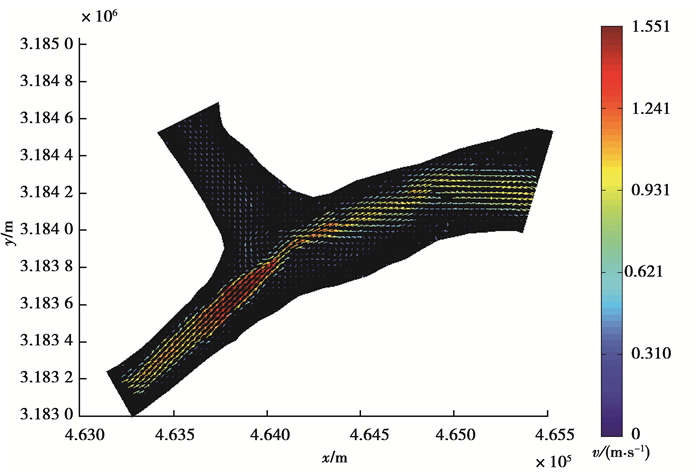
2.3 应用情况应用提出的核心算法,作者所在研究团队开发出了ezPIV表面流场测量系统,并成功应用于多个大型水利工程河工模型的分析测量工作中。图 7展示了对向家坝长河段模型(原型尺寸:2 700 m×2 200 m)的测量结果。这里需要说明的一点是本系统的流速测量范围与河工模型的比例尺有关,流速测量的上限也并非前文测试中的1.5 m/s,不同比例尺下的河工模型对应的流速测量范围不同。
|
图 7 向家坝长河段测量结果 Figure 7 Measurement results of Changhe section of Xiangjia dam |
研究提出的基于图像局部特征的河工模型表面流场测量方法,利用二值化局部特征方法获取流速矢量,不仅在常规流速区间(即0.1~1.0 m/s)测量准确率较高,而且在准静态流场(即0.01~0.1 m/s)或高速流场(即1.0~1.5 m/s)的测量中精度依然表现较好。同时,支持视频采集设备的主光轴与流场表面成任意角度架设,免去了预标定的繁琐过程,也提高了对复杂地形和光照变化的鲁棒性。另外,支持任意类型的示踪粒子,可有效降低测量成本。同时,提出的方法所使用的碎纸屑示踪粒子具有不规则性和分布密集性,相比于现有的标准圆形示踪粒子更接近流场的原观表面,所以在原观表面流场测量方面,提出的方法也具有一定的应用潜力。
| [1] |
Lingam M, Morrison P J. The action principle for generalized fluid motion including gyroviscosity[J]. Physics Letters A, 2014, 378(47): 3526-3532. DOI:10.1016/j.physleta.2014.10.013 |
| [2] |
Töger J, Bidhult S, Revstedt J, et al. Independent validation of four-dimensional flow MR velocities and vortex ring volume using particle imaging velocimetry and planar laser-Induced fluorescence[J]. Magnetic Resonance in Medicine, 2016, 75(3): 1064-1075. DOI:10.1002/mrm.v75.3 |
| [3] |
Li Y, Yang W, Xie C, et al. Gas/oil/water flow measurement by electrical capacitance tomography[J]. Measurement Science and Technology, 2013, 24(7): 74-80. |
| [4] |
Birkhofer B, Meile T, Cesare G D, et al. Use of gas bubbles for ultrasound doppler flow velocity profile measurement[J]. Flow Measurement and Instrumentation, 2016, 52-60. |
| [5] |
Dussol D, Druault P, Mallat B, et al. Automatic dynamic mask extraction for PIV images containing an unsteady interface, bubbles, and a moving structure[J]. Comptes rendus-Mécanique, 2016, 344(7): 464-478. DOI:10.1016/j.crme.2016.03.005 |
| [6] |
White D J, Take W A, Bolton M D. Soil deformation measurement using particle image velocimetry (PIV) and photogrammetry[J]. Geotechnique, 2003, 53(7): 619-632. DOI:10.1680/geot.2003.53.7.619 |
| [7] |
Lapinski M, Rostovtsev Y V. Measurement of the velocity of a quantum object:A role of phase and group velocities[J]. Optics Communications, 2017, 396: 169-173. DOI:10.1016/j.optcom.2017.03.061 |
| [8] |
Tauro F, Piscopia R, Grimaldi S. Streamflow observations from cameras:large-scale particle image velocimetry or particle tracking velocimetry[J]. Water Resources Research, 2017, 53(2): 38-42. |
| [9] |
Fu S, Biwole P H, Mathis C. Numerical and experimental comparison of 3D particle tracking velocimetry (PTV) and Particle Image Velocimetry (PIV) accuracy for indoor airflow study[J]. Building and Environment, 2016, 100: 40-49. DOI:10.1016/j.buildenv.2016.02.002 |
| [10] |
Kashyap M, Chalermsinsuwan B, Gidaspow D. Measuring turbulence in a circulating fluidized bed using PIV techniques[J]. Particuology, 2011, 9(6): 572-588. DOI:10.1016/j.partic.2011.06.007 |
| [11] |
Biswas N, Roy P C, Manna N K, et al. Experimental studies of flow through radial channels using PIV technique[J]. Journal of Visualization, 2014, 17(3): 221-233. DOI:10.1007/s12650-014-0201-x |
| [12] |
Parsapour-Moghaddam P, Rennie C D. Calibration of a 3D hydrodynamic meandering river model using fully spatially distributed 3D ADCP velocity data[J]. Journal of Hydraulic Engineering, 2018, 144(4): 38-42. |
| [13] |
Yang B, Wang Y, Liu J. PIV measurements of two phase velocity fields in aeolian sediment transport using fluorescent tracer particles[J]. Measurement, 2011, 44(4): 708-716. DOI:10.1016/j.measurement.2011.01.007 |
| [14] |
Shi B, Wei J, Pang M. A modified optical flow algorithm based on bilateral-filter and multi-resolution analysis for PIV image processing[J]. Flow Measurement and Instrumentation, 2014, 38(2): 121-130. |
| [15] |
Particle image velocimetry: Progress towards industrial application[M]. UK: Springer Science & Business Media, 2013.
|
| [16] |
Kähler C J, Scharnowski S, Cierpka C. On the resolution limit of digital particle image velocimetry[J]. Experiments in Fluids, 2012, 52(6): 1629-1639. DOI:10.1007/s00348-012-1280-x |
| [17] |
Gunawan B, Sun X, Sterling M, et al. The application of LS-PIV to a small irregular river for inbank and overbank flows[J]. Flow Measurement and Instrumentation, 2012, 24(2): 1-12. |
| [18] |
Persoons T, O'Donovan T S. High dynamic velocity range particle image velocimetry using multiple pulse separation imaging[J]. Sensors, 2011, 11(1): 1-18. DOI:10.1109/JSEN.2010.2096991 |
| [19] |
Li Z, Yang J, Zhao J, et al. PIMR:parallel and integrated matching for raw data[J]. Sensors, 2016, 16(1): 54. DOI:10.3390/s16010054 |
 2018, Vol. 41
2018, Vol. 41


