2. 河南省瓦斯地质与瓦斯治理重点实验室——省部共建国家重点实验室培育基地, 河南理工大学, 河南 焦作 454001;
3. 山东科技大学 矿山灾害预防与控制重点实验室, 山东 青岛 266590
2. State Key Laboratory Cultivation Base for Gas Geology and Gas Control, Henan Polytechnic University, Jiaozuo 454001, Henan, P. R. China;
3. Key Laboratory of Mine Disaster Prevention and Control, Shandong University of Science and Technology, Qingdao 266590, Shandong, P. R. China
随着煤炭开采深度的增加,瓦斯带来的安全隐患和危害日益突出,如煤壁、煤巷壁、煤层钻孔瓦斯涌出不确定性,加上中国煤层瓦斯“两高三低”赋存特点[1],使得矿井瓦斯严重威胁着井下安全生产,准确预测并解决矿井瓦斯灾害问题,国内外学者进行了大量的研究,主要集中在瓦斯突出的发生条件、煤层中瓦斯流动理论、外界条件改变时煤层瓦斯流动特征等方面。其中,鲜学福院士等[2]研究了煤与瓦斯突出的激发和发生条件,揭示了煤与瓦斯突出的主要能量是瓦斯膨胀能,并基于对Drucker理论的修正,提出了划分煤与瓦斯突出潜在危险区的基本方法[3];文献[4]在研究瓦斯流动时,将煤层内瓦斯流动分为两步进行,即第一步以菲克扩散形式,第二步以达西定律的形式;周世宁院士[5]从渗流力学角度提出瓦斯在煤层中的流动理论,即在煤层中任一点的流动速度与压力梯度成正比;郭勇义等[6]结合相似理论,求解了一维煤层瓦斯渗流微分方程的近似解析解,提出了修正的瓦斯流动方程式;孙培德等[7]进一步发展了非均质条件下煤层瓦斯流动数学理论模型,并通过数值模拟对模型进行了计算比较,认为该模型比均质条件下建立的瓦斯流动数学模型更能符合煤矿现场实际情况;Airey[8]根据煤本身性质及所处的外部条件,得出了瓦斯吸附解吸的宏观表达式;赵洪宝等[9]发现了瓦斯在煤体中的渗流存在一个渗流困难应力点,该参数可用于指导预防煤与瓦斯突出事故和提高瓦斯抽采效率;尹光志等[10]通过研究煤岩全应力应变过程中瓦斯流动特性,表明煤岩受载损伤演化过程决定了其内部瓦斯流动特性;赵洪宝等[11]研究了含瓦斯煤样横向变形与瓦斯流动的耦合关系,其横纵应变特性可用二次函数表征;Nandi等[12]和Bielicki等[13]通过改变煤样瓦斯吸附平衡压力,得出煤样吸附压力越大,放散系数越高的规律。
虽然在该领域的研究已经取得了丰硕的成果,但目前的研究仍然存在一些不可忽视的问题。如目前实验室内对煤层瓦斯放散规律研究多以一定颗粒度的煤粉为研究对象[14-17],而没有将煤作为一个整体来考虑,也忽略了煤自身结构对瓦斯放散的影响,使研究结果与实际生产情况差距过大,不能很好反映现场实际规律。基于此,笔者以一定尺度的型煤煤样模拟不同放散面积对瓦斯放散特性的影响,采用自主研发的试验装置研究放散面积对瓦斯放散的影响,其试验规律更接近于实际生产情况。这对准确预测瓦斯涌出,提高瓦斯抽采率,改善井下作业环境有重要意义。
1 试样制备与试验设备 1.1 试样制备由于天然煤体强度低、脆性大等特点,使得原煤取芯直接制作块煤难度很大,并且煤体内部层理和节理纵横交错,即使成功制成煤样,各个煤样的差异性也较大,因而不能准确地揭示瓦斯放散规律,所以这里采用型煤试件来进行研究。虽然原煤与型煤之间物理参数有所不同,如孔隙度、孔隙体积、原煤的杨氏模量及强度等,但用型煤做相关试验能得到良好的规律性。此外,相对于原煤,型煤试件离散性更小,各个试件之间的差异更小,使得试验规律性更为明显。
试验用煤块取自于山西省鹿台山煤业,在去除矸石后装袋密封运回,用破碎机破碎成煤粉,筛选出0.25~0.50 mm间煤粉颗粒,将选好煤粉和水泥、水按一定比例混合均匀。用天平称取上述煤粉混合物525 g放入设计的制型煤装置中,通过加压(25 MPa)和脱模两道工序制成70 mm×70 mm×70 mm型煤如图 1所示。

|
图 1 型煤煤样 Figure 1 Coal briquette specimen |
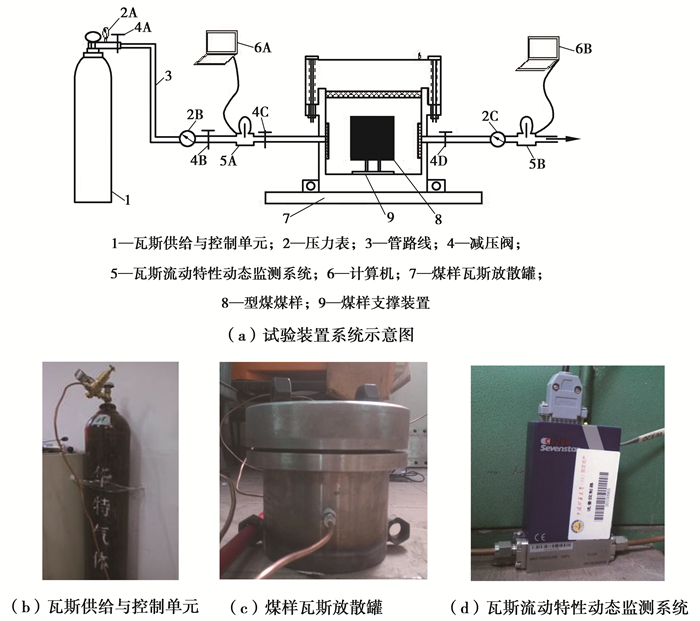
为了研究放散面积对型煤瓦斯放散特性影响,自主设计研发了一套型煤瓦斯放散试验装置系统,该装置主要包括瓦斯供给与控制单元、煤样罐及管路单元及瓦斯动态监测单元等,如图 2所示。由于本试验的特殊要求,型煤在煤样罐内处于准悬空状态,以实现其6面处于自由状态,所以在煤样罐腔体内安装一个便于拆卸的型煤支撑装置。该装置主要组成有2个平放于腔体底部薄磁片,磁片两侧各放一对小铁柱,4个铁柱支撑起型煤,薄磁片主要作用是使小铁柱稳定。
|
图 2 型煤煤样瓦斯放散试验装置系统 Figure 2 Coal briquette specimens gas dispersion test device |
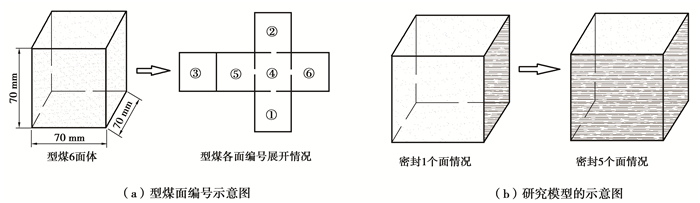
在研究放散面积对型煤瓦斯放散影响时,主要通过控制放散面积大小和改变放散面位置来研究其对瓦斯放散的影响,首先对型煤6个面编号,如图 3所示。
|
图 3 试样及研究模型 Figure 3 Sample and Research model |
进行试验研究时,依次密封试样的各面,形成不同放散面积的情况,如图 3(b)所示。若认为试样内含有的瓦斯在各方向上(X、Y、Z)是均匀分布的,则密封1个面时试样内瓦斯将有5个运移方向、5个放散面,而密封5个面时试样内瓦斯则只有1个运移方向、1个放散面,其他情况将介于此二者之间。
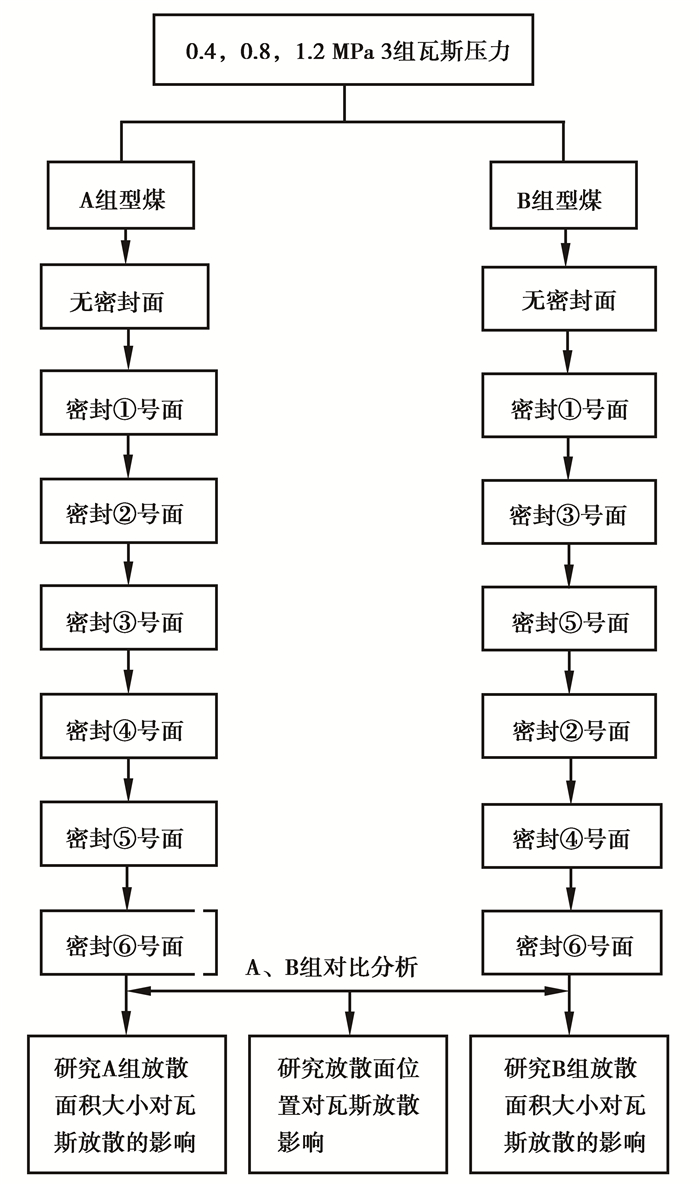
在试验方案流程图中(见图 4),A或B组型煤试验主要研究放散面积大小对瓦斯放散的影响,通过A组型煤与B组型煤试验做比较来研究放散面位置对瓦斯放散的影响。
|
图 4 试验方案流程图 Figure 4 Flow chart of test scheme |
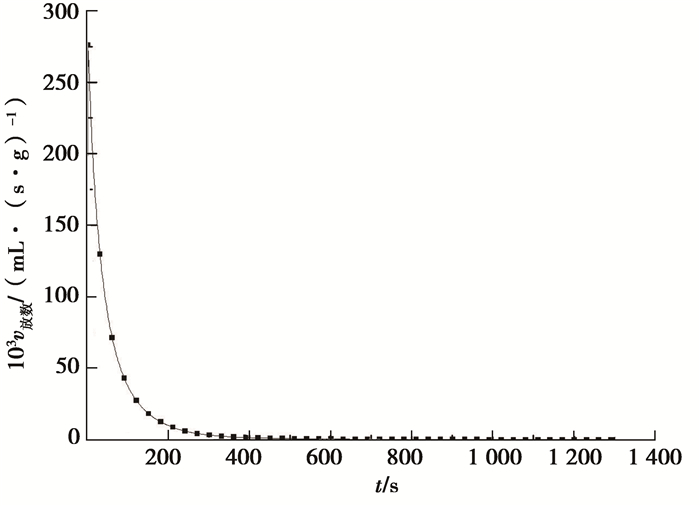
试验结果显示:放散面积对瓦斯放散过程存在影响,但并不改变瓦斯放散的总体趋势。各组数据的速度曲线具有很好的一致性,现取具有代表性的1.2 MPa瓦斯压力A组无密封处理条件下得到的瓦斯放散速度曲线为例,如图 5所示。瓦斯放散速度随着时间而减小,瓦斯放散曲线呈近似“L”型。在最初的几十秒放散速度很大,大多集中于0.1~0.3 mL/(s·g),放散时间至200 s时放散速度减小至0.01 mL/(s·g)以下,当放散1 200 s左右,放散速度减小至0.000 005 mL/(s·g)以下,认为放散过程基本结束。
|
图 5 瓦斯放散速度全过程图(1.2 MPa) Figure 5 The diagram of gas diffusion process |
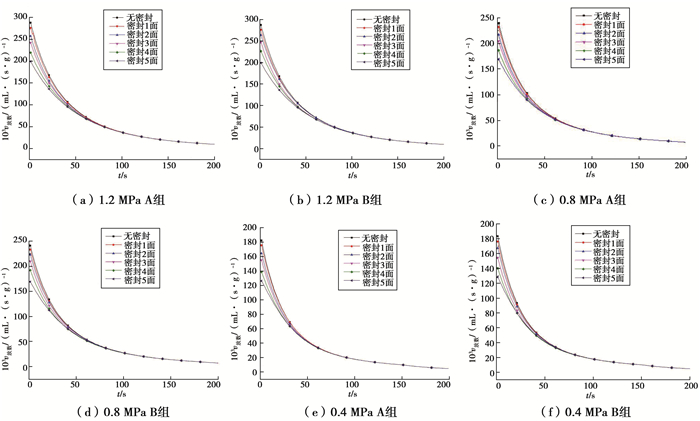
为了更有效地分析放散面积对瓦斯放散速度的影响,将瓦斯放散全过程分为拐点之前的急剧减小区和拐点之后的缓慢减小区(见图 6)。
|
图 6 急剧减小区瓦斯放散速度图 Figure 6 The diagram of gas diffusion process in rapidlydereasing area |
从图 6可以看出:
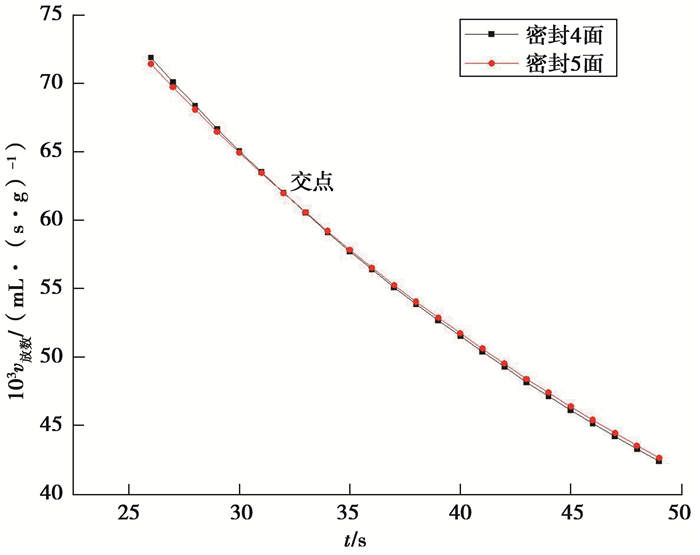
1) 在瓦斯放散初期相同平衡压力条件下,放散速度随放散面积的减小而减小,其随放散时间的延长差距也逐渐在减小。随着瓦斯放散试验的进行,出现了放散面积小的型煤其放散速度反而大于放散面积大的型煤放散速度现象,为了便于研究,将此现象定义为速度“超越”,这种速度“超越”现象在拐点处最为频繁并将此延续到拐点后的缓慢减小区,由于这种交点较多,选取0.4 MPa A组型煤瓦斯放散曲线进行描述,如图 7所示。
|
图 7 瓦斯放散曲线交点图 Figure 7 The diagram of gas diffusion curve intersection |
分析原因:
a.在瓦斯放散初期,主要是放散面附近与型煤裂隙内的游离瓦斯和部分吸附瓦斯从放散面逸出。放散面积越大,放散初期速度就越大,随着放散进行,放散面周围瓦斯排出,游离瓦斯在型煤内裂隙系统中流动,此流动属于渗透性流动,此时放散速度主要由渗流速度决定;而密封型煤表面造成了游离瓦斯在渗透作用下所走的路径变长,渗透阻力变大,因此渗流速度变小。综合以上两个因素,造成了实验室出现的在初始阶段放散速度随放散面积减小而减小现象。
b.随着放散持续进行,渗透作用效果在减小,由于前期煤体裂隙中游离瓦斯大量涌出,在型煤裂隙系统与煤基质(颗粒煤)之间形成了瓦斯浓度差,颗粒煤孔隙系统内游离瓦斯开始在浓度梯度作用下扩散到型煤裂隙系统中,此过程主要发生于从颗粒煤孔隙到周围裂隙之间,此时瓦斯放散速度主要由扩散速度决定。在此放散过程中,由于放散面附近较密封面初期解吸出更多的瓦斯,使得放散一段时间后出现放散面积大的型煤比放散面积小的型煤内瓦斯浓度低的现象,而扩散速度的大小主要受浓度差控制。
在此阶段出现速度“超越”现象,由此也可以推出,在瓦斯放散曲线拐点附近就是型煤放散过程中渗透扩散起主导作用的过渡阶段。在相同瓦斯平衡压力下,放散面积大的型煤瓦斯放散速度在放散初始阶段较大,一段时间后,由于放散速度主要受扩散影响,放散面积大的型煤瓦斯放散速度反而又略低于放散面积小的型煤。
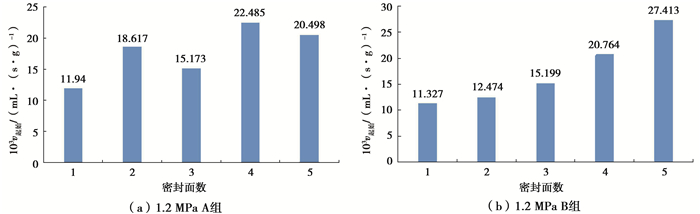
2) 密封型煤同一方向2个面时,发现密封第2个面比第1个面对瓦斯放散速度影响大,并发现随着放散面积减小,其对瓦斯放散影响效果更加明显,特别是对瓦斯初始放散速度影响更为明显。图 8为在1.2 MPa瓦斯压力下A、B两组型煤试验瓦斯放散起始速度减小值。
|
图 8 密封各面放散初始速度减小值柱状图 Figure 8 The bar chart of decrease of initial diffusion velocity by sealing the surface |
A组中密封1,3,5面和B组中密封1,2,3面时都是对型煤3个方向首次密封,A组中密封2,4面和B组中密封4,5面是对型煤3个方向中其中2个方向的第2次密封。从图 8中可以清晰看出,在密封同一“性质”(同一方向的第1次密封,第2次密封)放散面时,随着密封试验的进行,瓦斯放散起始速度减小值越来越大;密封同一方向时,第2次密封比第1次密封影响大得多。
分析原因:
在开始无密封时,瓦斯在型煤中流动属于球向流动,当1个方向2个面都被密封其他2个方向对瓦斯开放时,瓦斯在型煤中流动由球向流动变为径向流动;当其中2个方向全被密封只剩1个方向瓦斯能够流动时,瓦斯在型煤中流动由径向流动变为单向流动。
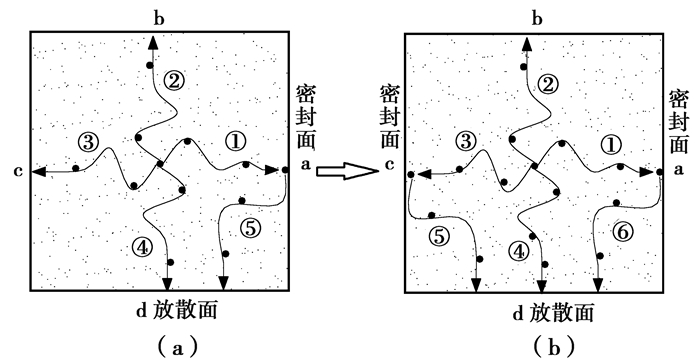
如图 9所示为型煤其中一个横截面,其中(a)图中的a面为密封面,b、c、d为放散面,(b)图中的a、c面为密封面,b、d为放散面,①②③④⑤⑥为瓦斯分子流动的路径示意。
|
图 9 密封型煤对立面时内部瓦斯流动形式示意图 Figure 9 Schematic diagram of internal gas flow when sealing two facing surfaces |
从图 9可知:当密封a面时瓦斯分子可以从b、c、d面放散出,运动轨迹如②③④所示,而流向a面的瓦斯分子由于放散面被密封最后从b、c、d面放散出,运动轨迹如①⑤所示,因此型煤中瓦斯分子在密封放散面前从a、b、c、d放散出的球向流动变为从b、c、d放散出的径向流动;当密封a、c面(对立面)时瓦斯分子可以从b、d面放散出,运动轨迹如②④所示,而流向a、c面的瓦斯分子由于放散面被密封最后从b、d面放散出,运动轨迹如①③⑤⑥所示,因此型煤中瓦斯分子在密封c面前从b、c、d面放散出的径向流动变为从b、d放散出的单向流动。
因此,一个方向上第2次密封与第1次密封相比较,不单是放散面积在减小,更重要的是型煤内的瓦斯流动形式发生了改变,最终出现同一方向第2次密封比第1次密封影响大。
利用origin软件对数据拟合发现,在拐点之前用幂函数拟合曲线的拟合度最高,相关度达到0.95以上,其他函数均未达到0.90。取在1.2 MPa瓦斯压力下A组所做的实验组,对该段数据进行拟合,拟合结果如表 1所示。
| 表 1 瓦斯放散拟合函数 Table 1 The fitting function of gas emission |
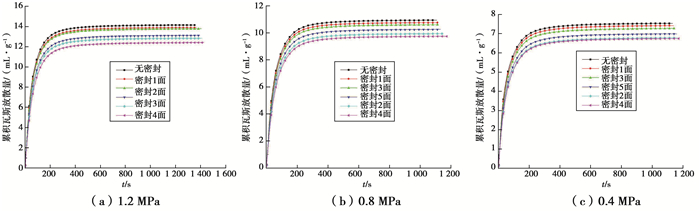
3) 拐点后缓慢减小区。由图 10瓦斯放散曲线可知,缓慢减小区经历时间较长,但此过程瓦斯放散速度较小。在开始的时候,只有部分曲线完成速度“超越”,到曲线结尾阶段,全部曲线完成超越。由于试验条件有限,将瓦斯放散速度减小到0.000 005 mL/(s·g)时视为放散结束,发现随着试验进行,放散面积越来越小,瓦斯放散持续时间越来越长。如图 10为2试验组在1 253 s时瓦斯放散速度图。
|
图 10 在1 253 s时2试验组瓦斯放散速度图 Figure 10 Gas emission velocity diagram of two test groups at 1 253 s |
分析原因:
a.由于缓慢减小区刚开始型煤内属于渗透运动和扩散运动过渡阶段,在渗透运动中,放散面积越大,渗透阻力越小,渗透速度越大;在扩散运动中,放散面积越大,前期放散瓦斯越多;在后期煤样内瓦斯浓度相对较低,所以放散速度就低。综合上述两种原因,产生在缓慢减小区刚开始的时候,只有部分曲线完成速度“超越”,放散随着时间继续进行,渗透作用在减弱,扩散运动在加强,到放散后期,扩散运动占主导作用。因此,放散速度由型煤内瓦斯浓度决定,放散面积越小,型煤内瓦斯浓度就越高,扩散运动就越明显,放散速度就越快。
b.由于型煤试样中参与瓦斯放散的煤体范围是由放散面及型煤内裂隙附近组成的,随时间逐渐向其周围深部延伸,这种影响的时效性导致深部瓦斯放散的起始时间较晚,再加上深部煤颗粒距型煤内裂隙或放散面较远,深处瓦斯涌出型煤的运移路径增长,流动过程中需克服阻力更大,导致这部分瓦斯解吸放散较为缓慢,后期型煤煤样内瓦斯浓度较高。综上两点,深部瓦斯放散起始时间较迟,且放散过程较为缓慢,瓦斯扩散运动持续时间就越长,因此放散所需时间较长。
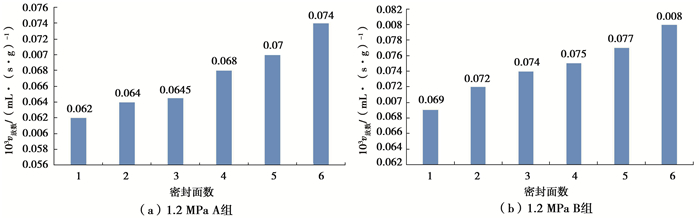
2.3 放散面积对瓦斯放散量的影响如图 11所示,在0.4,0.8,1.2 MPa瓦斯压力下,B组型煤在不同放散面积的条件下瓦斯气体有如下放散规律:
|
图 11 不同瓦斯压力下不同放散面积型煤累计瓦斯放散量 Figure 11 Cumulative diffusion gas under different gas pressure in different surface area |
1) 不同放散面积瓦斯气体的累计放散量与时间的关系曲线仍然是有限单调增函数,即不同放散面积瓦斯放散量随时间变化规律基本一致,放散面积的改变并没有改变瓦斯放散规律。
2) 在不同的瓦斯压力(0.4,0.8,1.2 MPa)试验结果皆表现出:随着型煤放散面积的减小,在相同时间段,累积放散量均减小;相同平衡压力下,由于不同放散面积的型煤瓦斯放散速度曲线出现交叉点,所以在交叉点之前,累积瓦斯放散量差距越来越大,并在交叉点处达到差距最大,随后这种差距逐渐减小并最终趋于稳定;但在累积瓦斯放散曲线中,并未出现如放散速度曲线那样的交叉点,虽然差距在减小但这种差距并未消失。
3) 试验开始的前300 s内,不同放散面积的型煤瓦斯累积放散量之差随时间增加得较显著;300 s后,两者差距变化较小。主要原因是型煤瓦斯放散初始阶段,试样放散面或裂隙中的游离瓦斯首先涌出,放散面积越大,型煤内瓦斯渗透运动越强烈,使得各组试验中瓦斯放散量差别较为明显,当试样中的游离瓦斯大部分解吸后渗流作用不突出时,两者累积放散量的差距也将不再明显变化。
4) 不同瓦斯压力下,型煤的瓦斯累积放散量呈增速上升,该单调递增函数曲线的上限为极限瓦斯放散量,即型煤理论上的最大瓦斯放散量。放散初期,因型煤内有大量游离瓦斯涌出,造成初期瓦斯放散速度较大,累积瓦斯放散量急速增加;随着瓦斯放散速度的衰减,瓦斯累积放散量的增加趋势也逐渐趋于平缓,最终瓦斯放散速度几乎衰减至0,此时试样的累积瓦斯放散量即为极限瓦斯放散量,但试验时无法获得此值,只能得出减小到设定值累积放散量。
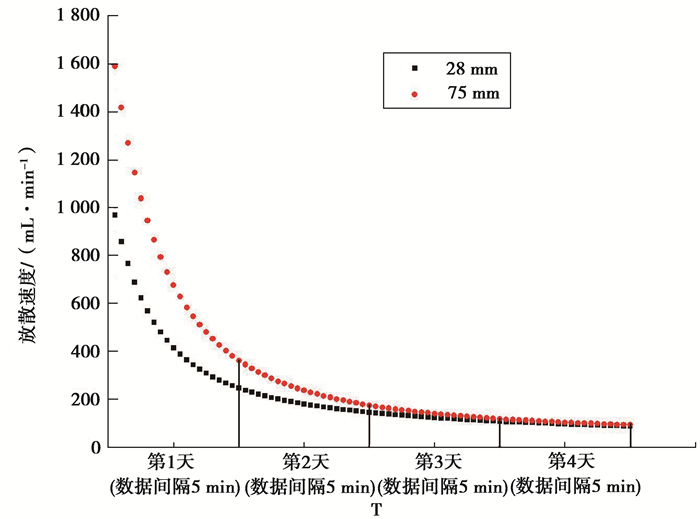
3 现场实测对比分析以山西鹿台山煤矿煤层钻孔监测为工程背景,通过现场监测鹿台山2#煤层钻孔瓦斯放散情况来进一步验证放散面积对型煤瓦斯放散影响特征的适用性,将实验室试验瓦斯规律应用到工程实践中。在现场施工中瓦斯抽采钻孔采用直径28 mm和75 mm 2种,钻孔长度为10 m,角度采用与煤壁夹角呈45°方向,连续监测4 d,每天监测2 h,每次记录间隔5 min监测这2个钻孔瓦斯放散情况,获得现场实测瓦斯钻孔瓦斯放散特性,如图 12所示。
|
图 12 钻孔瓦斯流速监测情况 Figure 12 Monitoring of borehole gas flow rate |
由图 12可以看出,2种直径钻孔的瓦斯放散速度随着监测时间增加逐渐降低,但放散速度降低的幅度不相同。因为直径为75 mm的钻孔瓦斯放散面积大于直径为28 mm的钻孔,所以前者的钻孔瓦斯放散速度比较大,两种钻孔直径的瓦斯放散速度曲线与型煤瓦斯放散曲线图近似相同。因此,放散面积对型煤瓦斯放散特征的影响规律与现场生产实际情况比较接近,将试验分析结果按某一方式加以适当修正后可用于指导现场实际生产。
4 结论1) 放散面积对型煤瓦斯放散速度的影响,其规律近似呈“L”型曲线,相同平衡压力条件下,在瓦斯放散初期瓦斯放散速度随放散面积的减小而减小,随放散时间的延长差距逐渐在减小,出现了速度“超越”现象,且这种速度“超越”现象在拐点处最为频繁并将此延续到拐点后的缓慢减小区。
2) 相同时间内,不同放散面积的累计瓦斯放散量与时间的关系曲线仍然是有限单调增函数,即放散面积的改变并没有改变瓦斯放散规律,但在不同的瓦斯压力条件下,累积放散量随着型煤放散面积的减小而减小。
3) 放散面积对型煤瓦斯放散的影响主要改变了型煤内瓦斯流动的形式,表现为:在开始无密封时,瓦斯在型煤中流动属于球向流动,当一个方向2个面都被密封其他2个方向对瓦斯开放时,瓦斯在型煤中流动由球向流动变为径向流动,当其中2个方向全被密封只有1个方向瓦斯能够流动时,瓦斯在型煤中流动由径向流动变为单向流动。因此,型煤密封面增多,不单是放散面积在减小,更重要的是型煤内的瓦斯流动形式发生了改变。
4) 通过现场监测不同直径煤层钻孔的瓦斯放散情况与实验室试验放散面积对型煤瓦斯放散特性影响规律基本一致,可将试验分析结果按某一方式加以适当修正后用于指导现场实际生产。
| [1] |
李树刚, 李志梁, 林海飞, 等. 对采动裂隙演化规律的影响研究[J]. 矿业安全与环保, 2015, 42(5): 25-28. LI Shugang, LI Zhiliang, LIN Haifei, et al. Research on influent of mining height on mining fissure evolution[J]. Mining Safety & Environmental Protection, 2015, 42(5): 25-28. (in Chinese) DOI:10.3969/j.issn.1008-4495.2015.05.007 |
| [2] |
鲜学福, 辜敏, 李晓红, 等. 煤与瓦斯突出的激发和发生条件[J]. 岩土力学, 2009, 30(3): 577-581. XIAN Xuefu, GU min, LI Xiaohong, et al. Excitation and occurrence conditions for coal and gas outburst[J]. Rock and Soil Mechanics, 2009, 30(3): 577-581. (in Chinese) DOI:10.3969/j.issn.1000-7598.2009.03.001 |
| [3] |
鲜学福, 许江, 王宏图. 煤与瓦斯突出潜在危险区(带)预测[J]. 中国工程科学, 2001, 3(2): 39-46, 51. XIAN Xuefu, XU Jiang, WANG Hongtu. Predication of potential danger region (zone) of coal and gas outburst[J]. Engineering Science, 2001, 3(2): 39-46, 51. (in Chinese) DOI:10.3969/j.issn.1009-1742.2001.02.009 |
| [4] |
Oda M, Takemura T, Aoki T. Damage growth and permeability change in triaxial compression tests of Inada granite[J]. Mechanics of Materials, 2002, 34(6): 313-331. DOI:10.1016/S0167-6636(02)00115-1 |
| [5] |
周世宁. 瓦斯在煤层中流动的机理[J]. 煤炭学报, 1990, 15(1): 15-24. ZHOU Shining. Mechanism of gas flow in coal seams[J]. Journal of China Coal Society, 1990, 15(1): 15-24. (in Chinese) |
| [6] |
郭勇义, 周世宁. 煤层瓦斯一维流场流动规律的完全解[J]. 中国矿业学院学报, 1984, 2(2): 19-28. GUO Yongyi, ZHOU Shining. Complete solutions of the law of gas flow in coal seams with one dimensional gas flow fields[J]. Journal of China University of Mining & Technology, 1984, 2(2): 19-28. (in Chinese) |
| [7] |
孙培德. 瓦斯动力学模型的研究[J]. 煤田地质与勘探, 1993, 21(1): 32-40. SUN Peide. Study of the gas flow mathematical models[J]. Coal Geology & Exploration, 1993, 21(1): 32-40. (in Chinese) |
| [8] |
Airey E M. Gas emission from broken coal. An experimental and theoretical investigation[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1968, 5(6): 475-494. |
| [9] |
赵洪宝, 尹光志, 李小双. 突出煤渗透特性与应力耦合试验研究[J]. 岩石力学与工程学报, 2009, 28(s2): 3357-3362. ZHAO Hongbao, YIN Guangzhi, LI Xiaoshuang. Test study on coupling relationship between permeability characteristics and stress of outburst coal[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(s2): 3357-3362. (in Chinese) |
| [10] |
尹光志, 李广治, 赵洪宝, 等. 煤岩全应力-应变过程中瓦斯流动特性试验研究[J]. 岩石力学与工程学报, 2010, 29(1): 170-175. YIN Guangzhi, LI Guangzhi, ZHAO Hongbao, et al. Experimental research on gas flow properties of coal specimens in complete stress-strain process[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 170-175. (in Chinese) |
| [11] |
赵洪宝, 李华华, 杜秋浩, 等. 含瓦斯煤样横向变形与瓦斯流动特性耦合关系试验研究[J]. 岩土力学, 2013(12): 3384-3402. ZHAO Hongbao, LI Huahua, DU Qiuhao, et al. Experimental study of coupling relationship between lateral strain of coal containing gas and characteristics of gas flow[J]. Rock and Soil Mechanics, 2013(12): 3384-3402. (in Chinese) |
| [12] |
Nandi S P, Walker P L Jr. Activated diffusion of methane in coal[J]. Fuel, 1970, 49(3): 309-323. DOI:10.1016/0016-2361(70)90023-2 |
| [13] |
Bielicki R J, Perkins J H, Kissell F N. Methane diffusion parameters for sized coal particles:a measuring apparatus and some preliminary results[M]. Washington, D.C.: U S Dept of Interior Bureau of Mines, 1972.
|
| [14] |
Qin Yueping, Wang Yaru, Yang Xiaobin, et al. Experimental study on dynamic gas adsorption[J]. International Journal of Mining Science and Technology, 2012, 22(6): 763-767. DOI:10.1016/j.ijmst.2012.11.010 |
| [15] |
聂百胜, 郭勇义, 吴世跃. 煤粒瓦斯扩散的理论模型及其解析解[J]. 中国矿业大学学报, 2001, 30(1): 19-22. NIE Baisheng, GUO Yongyi, WU Shiyue. Theoretical model of gas diffusion through coal particles and its analytical solution[J]. Journal of China University of Mining & Technology, 2001, 30(1): 19-22. (in Chinese) DOI:10.3321/j.issn:1000-1964.2001.01.005 |
| [16] |
李志强, 刘勇, 许彦鹏. 煤粒多尺度孔隙中瓦斯扩散机理及动扩散系数新模型[J]. 煤炭学报, 2016, 41(3): 633-643. LI Zhiqiang, LIU Yong, XU Yanpeng. Gas diffusion mechanism in multi-scale pores of coal particles and new diffusion model of dynamic diffusion coefficient[J]. Journal of China Coal Society, 2016, 41(3): 633-643. (in Chinese) |
| [17] |
秦跃平, 王翠霞, 王健, 等. 煤粒瓦斯放散数学模型及数值解算[J]. 煤炭学报, 2012, 37(9): 1466-1471. QIN Yueping, WANG Cuixia, WANG Jian, et al. Mathematical model of gas emission in coal particles and the numerical solution[J]. Journal of China Coal Society, 2012, 37(9): 1466-1471. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41


 ,
,