2. 中国石油集团电能公司 中油电能电力技术服务公司, 黑龙江 大庆 163453
2. Electric Technical Services Company, China Petroleum Electric Energy Co., Ltd, Daqing 163453, Heilongjiang, P. R. China
传统分布式电源(distributed generation,DG)优化配置问题主要围绕风电(wind generation,WG)和光伏(photovoltaic,PV)并网运行。随着电力工业和电力电子技术的发展,电动汽车(plug-in electric vehicle,PEV)作为一种更加经济的手段接入电网。合理配置DG和PEV可以有效降低系统网损,提高供电可靠性和灵活性[1]。然而DG和PEV也给电力系统带来了较强的随机性和间歇性,同时DG出力的相关性也影响节点电压的波动性[2]。因此,在配电网优化中必须考虑DG、PEV和负荷之间的随机性、间歇性以及相关性,为电网的安全运行奠定基础,满足智能电网的需求。
针对DG和PEV并网不确定性问题,国内外相关学者进行了相当多的研究。文献[3]考虑多风电场相关性对概率潮流计算的影响,采用K-means聚类和Copula函数建立场景概率潮流计算方法。文献[4]考虑分布式电源与负荷之间的相关性,采用无迹变换(unscented transformation,UT)将概率潮流转化为确定性最优潮流。文献[5]在文献[4]的基础上结合径向基神经网络(radial basis function,RBF),处理概率潮流中功率方程计算问题。针对DG和PEV并网优化问题,文献[6]考虑电压控制成本,以年综合成本和清洁能源发电占比为目标函数。文献[7]将环境效益纳入DG和PEV优化目标函数内,将自适应变异引入量子粒子群算法。文献[8]研究了分布式电源与微电网组合的混合供电方案,采用NSGA-Ⅱ算法求解集成供电系统中DG优化配置方案。文献[9]分析了DG出力相关性对节点电压的影响,提高了DG并网时的接入容量。
以往文献主要基于传统潮流计算方法求解DG和PEV的优化配置,忽略了他们之间的不确定性,且传统蒙特卡洛模拟采样复杂,计算负担重。笔者充分考虑WG、PV、PEV和负荷之间的随机性、间歇性和相关性,以DG总成本、供电可靠性和有功损耗建立目标函数模型,采用UT和RBF相结合求解概率潮流。UT比任何非线性函数更能近似其真实概率分布,保障了算法的精度,同时利用RBF求解非线性方程组的能力,避免了传统潮流计算所需计算偏导和雅可比矩阵,提高了算法运行的速度。采用基于成功历史的自适应参数差分进化算法(success-history based parameter adaptation for differential evolution,SHADE)对优化模型进行求解。以IEEE33节点配电系统为例,计算结果与差分进化蒙特卡洛(DE-MCS)和量子粒子群拉丁超立方蒙特卡洛(QPSO-CLMCS)进行对比,验证所提算法的有效性。
1 微电网中不确定性分量建模 1.1 WG概率模型双参数(规模参数c和形状参数k)的Weibull分布被用来描述风速v的变化规律,其概率密度函数为:
| $ f\left( v \right) = \frac{k}{c}\left( {\frac{v}{c}} \right)k - 1\exp \left[ { - {{\left( {\frac{v}{c}} \right)}^k}} \right]。$ | (1) |
风机输出功率PWT与风速v之间的函数关系表示为:
| $ {P_{{\rm{WT}}}} = \left\{ \begin{array}{l} 0,v \le {v_{{\rm{c}}i}},v \ge {v_{{\rm{co}}}},\\ {P_{\rm{r}}}\frac{{v - {v_{{\rm{c}}i}}}}{{{v_{\rm{n}}} - {v_{{\rm{c}}i}}}},{v_{{\rm{c}}i}} \le v \le {v_{\rm{n}}},\\ {P_{\rm{r}}},{v_{\rm{n}}} \le v \le {v_{{\rm{co}}}}, \end{array} \right. $ | (2) |
式中:Pr为风机的额定功率;vci、vco和vn分别为切入风速、切出风速和额定风速[10],分别取4,25, 15 m/s。
1.2 PV概率模型太阳辐射r是影响光伏系统输出功率大小的主要因素。Beta分布被用来近似描述r在一定时间段内的分布,其概率密度函数[5]表示为:
| $ f\left( r \right) = \frac{{\mathit{\Gamma }\left( {\alpha + \beta } \right)}}{{\mathit{\Gamma }\left( \alpha \right)\mathit{\Gamma }\left( \beta \right)}}{\left[ {\frac{{r\left( t \right)}}{{{r_{\max }}}}} \right]^{\alpha - 1}}{\left[ {1 - \frac{{r\left( t \right)}}{{{r_{\max }}}}} \right]^{\beta - 1}}, $ | (3) |
式中:α和β分别为Beta分布的2个形状参数;rmax为某时段内的最大太阳辐射。光伏发电系统的输出功率PPV与太阳辐射r的函数关系可以表示为:
| $ {P_{{\rm{PV}}}} = \left\{ \begin{array}{l} {P_{{\rm{rn}}}}\frac{{{r^2}}}{{{R_{{\rm{std}}}}{R_{\rm{c}}}}},0 \le r \le {R_{\rm{c}}},\\ {P_{{\rm{rn}}}}\frac{r}{{{R_{{\rm{std}}}}}},{R_{\rm{c}}} \le r \le {R_{{\rm{std}}}},\\ {P_{{\rm{rn}}}},r \ge {R_{{\rm{std}}}}, \end{array} \right. $ | (4) |
式中:Prn为光伏发电系统额定功率;Rc为确定点的太阳辐射,通常设置为150 W/m2;Rstd为标准测试环境下的太阳辐射,通常设置为1 000 W/m2。
1.3 PEV概率模型考虑到PEV采用无序充电模式,采用(文献[11]所示模型),采用极大似然估计法求得日行驶里程d近似服从对数正态分布,其概率密度函数如式(5)所示;根据NHTS的统计结果,起始充电时刻T(即最后一次出行返回时刻)近似服从正态分布,其概率密度函数如式(6)所示。
| $ f\left( d \right) = \frac{1}{{\sqrt {2\pi d} {\sigma _d}}}\exp \left[ { - \frac{{{{\left( {\ln d - {\mu _d}} \right)}^2}}}{{2\sigma _d^2}}} \right], $ | (5) |
| $ f\left( T \right) = \left\{ \begin{array}{l} \frac{1}{{\sqrt {2\pi } {\sigma _T}}}\exp \left[ { - \frac{{{{\left( {T - {\mu _T}} \right)}^2}}}{{2\sigma _T^2}}} \right],\\ \frac{1}{{\sqrt {2\pi } {\sigma _T}}}\exp \left[ { - \frac{{{{\left( {T + 24 - {\mu _T}} \right)}^2}}}{{2\sigma _T^2}}} \right]。\end{array} \right. $ | (6) |
负荷具有时变性,可以用正态分布近似表示负荷功率的变化。节点i负荷的有功功率和无功功率概率密度函数为:
| $ f\left( {{P_{{\rm{Li}}}}} \right) = \frac{1}{{\sqrt {2\pi } {\sigma _i}}}\exp \left[ { - \frac{{{{\left( {{P_{{\rm{Li}}}} - P_{{\rm{Li}}}^{\rm{b}}} \right)}^2}}}{{2\sigma _i^2}}} \right], $ | (7) |
| $ f\left( {{Q_{{\rm{Li}}}}} \right) = {P_{{\rm{Li}}}}Q_{{\rm{Li}}}^{\rm{b}}/P_{{\rm{Li}}}^{\rm{b}}, $ | (8) |
式中:PLib、QLib分别为基态节点负荷有功功率和无功功率;σi为节点i负荷功率的标准差,这里取5%。
2 基于机会约束的多目标优化模型 2.1 目标函数1) DG设备运行总成本CDG,包括设备投资成本CT、运行维护成本COM和替换成本CR。
| $ {C_{{\rm{DG}}}} = {C_{\rm{T}}} + {C_{{\rm{OM}}}} + {C_{\rm{R}}} = \sum\limits_{i \in {N_{{\rm{DG}}}}} {\left( {C_i^{\rm{T}} + C_i^{{\rm{OM}}} + C_i^{\rm{R}}} \right){x_i}{P_i}} , $ | (9) |
式中:CiT、CiOM、CiR分别为电源i的投资成本、运维成本和替换成本;xi为电源i的数量;Pi为电源i的装机容量[10]。
2) 供电可靠性最大。供电可靠性是衡量供电系统电能质量的重要指标,合理配置DG可提高电网在孤岛运行时的供电可靠性。本文采用优化期内总缺供电量成本CEENS衡量DG并网后供电系统的可靠性[7]。
| $ {C_{{\rm{EENS}}}} = {C_{{\rm{ens}}}} \cdot {\beta _{{\rm{EENS}}}}, $ | (10) |
式中:Cens为单位缺供电量成本,取13.65 $/(kw·h);βEENS为期望缺供电量指标。
3) 有功损耗最小。有功损耗是衡量配电网经济运行的重要指标,合理配置DG和PEV可有效减少有功损耗,对提高配电网经济运行能力有重要意义。有功损耗的费用表示为:
| $ {C_{{\rm{ploss}}}} = \sum\limits_{t = 1}^T {{C_{\rm{e}}}{P_{{\rm{loss}}}}{T_{\max }}} , $ | (11) |
式中:Ce为单位电价,取0.089 $/(kw·h);Ploss为配电网网损;Tmax为年最大负荷利用时间(h),取8 760 h。
2.2 约束条件1) 功率平衡方程。
| $ \left. \begin{array}{l} {P_{\rm{G}}} - {P_{\rm{L}}} = {V_i}\sum\limits_{j = 1}^N {{V_j}\left( {{G_{ij}}\cos {\delta _{ij}} + {B_{ij}}\sin {\delta _{ij}}} \right)} ,\\ {Q_{\rm{G}}} - {Q_{\rm{L}}} = {V_i}\sum\limits_{j = 1}^N {{V_j}\left( {{B_{ij}}\cos {\delta _{ij}} - {G_{ij}}\sin {\delta _{ij}}} \right)} , \end{array} \right\} $ | (12) |
式中:PG、QG分别为节点i处电源输出的有功、无功功率;PL、QL分别为节点i处的有功、无功负荷。
2) 机会约束与不等约束。
对含DG的概率潮流计算时,还需考虑DG接入容量、DG渗透率、节点电压幅值和馈线传输容量的越限问题。笔者采用机会约束与不等式约束,对节点电压幅值和线路传输容量采用机会约束限制。
| $ \left. \begin{array}{l} \mathit{Pr}\left\{ {{V_{\min }} \le {V_i} \le {V_{\max }}} \right\} \ge \alpha ,\\ \mathit{Pr}\left\{ {{S_{ij}} \le {S_{ij\max }}} \right\} \ge \beta , \end{array} \right\} $ | (13) |
式中:Pr{·}为事件{·}成立的置信水平,节点电压幅值置信水平α和馈线传输容量的置信水平β均设为0.8[12]。
对DG接入容量,DG渗透率采用不等式约束限制。
| $ \left. {\begin{array}{*{20}{c}} {{P_{{\rm{EN}}}} = \left( {\sum\limits_{i = 1}^{{N_{{\rm{DG}}}}} {{P_{{\rm{DG}}i}}} } \right)/\left( {\sum\limits_{i = 1}^{{N_{{\rm{BUS}}}}} {{P_{Li}}} } \right) \le {P_{{\rm{ENmax}}}},}\\ {{S_{{\rm{DG}}i}} \le {S_{{\rm{DG}}i\max }},} \end{array}} \right\} $ | (14) |
式中:PEN、SDGi分别为DG渗透率和安装容量。
3 多目标优化模型求解 3.1 UT(RBF)求解概率潮流1) 采用UT将概率潮流问题转换为少量样本点的确定性潮流计算。如果输入随机变量X是具有均值ux和协方差Pxx的n维输入向量,输出向量Y可以通过一组非线性变换函数来实现。其中随机变量X之间的相关性根据各随机变量的标准差δi以及变量之间的相关系数ρij构造的协方差矩阵Pxx表示。采用对称采样策略参照文献[4],N个比例对称采样的Sigma点为:
| $ \left. \begin{array}{l} \left\{ {{\chi _0}} \right\} = {u_x},\\ \left\{ {{\chi _i}} \right\} = {u_x} + \alpha \sqrt {n/\left( {1 - {W_0}} \right)} {A_i},\\ \left\{ {{\chi _{n + i}}} \right\} = {u_x} - \alpha \sqrt {n/\left( {1 - {W_0}} \right)} {A_i}, \end{array} \right\} $ | (15) |
式中:α为比例缩放系数;Ai为A的第i列元素,其中A为对协方差矩阵Pxx进行Cholesky分解求得,相关系数的取值来源于文献[13];n为输入随机变量维数;{χi}表示第i个Sigma采样点,为n维列向量;W0为均值处Sigma点权值。对所选择的输入随机变量Sigma点集中的每个采样点进行非线性变换fU,得到变换后Sigma点集。
| $ {y_i} = {f_U}\left( {{{\rm{ \mathsf{ χ} }}_i}} \right)i = 1,2, \cdots ,N, $ | (16) |
输出随机变量Y的均值μy和协方差Pyy采用变换之后的Sigma点的加权样本均值和加权协方差来近似。
| $ {\mu _y} = \sum\limits_{i = 1}^N {W_i^m{y_i}} , $ | (17) |
| $ {\mathit{\boldsymbol{P}}_{yy}} = \sum\limits_{i = 1}^N {W_i^c\left( {{y_i} - {\mu _y}} \right){{\left( {{y_i} - {\mu _y}} \right)}^{\rm{T}}}} , $ | (18) |
式中:Wic、Wim分别为均值权重和协方差权重。
2) RBF用来解决DG和PEV在系统中功率方程计算的问题。RBF具有“任何非线性函数都可以通过具有零误差的RBF神经网络来近似”的优势。功率方程写成非线性方程组的形式:
| $ {y_i} = f\left( {{x_i}} \right), $ | (19) |
式中:xi代表潮流计算所要求得的节点i的电压和相角;yi表示节点i的有功功率和无功功率;f代表功率方程映射。
笔者选择非线性高斯激活函数构成隐含层,采用精确拟合法[14]训练RBF。隐含层的神经元数量等于输入向量的数量,将每个内核的中心设定在特定的输入向量上,忽略了隐含层的优化只需计算输出层的权重因子。因此网络的训练过程所需时间非常短,适用于迭代计算。针对输出层权重因子的优化,采用线性最小二乘回归来计算所得输出权重因子矩阵为:
| $ \mathit{\boldsymbol{W}} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{\left( {A{A^{\rm{T}}}} \right)^{ - 1}}, $ | (20) |
式中:W为输出层权重因子矩阵; T为目标输出向量; A为隐含层的输出矩阵。
3) 应用UT(RBF)求解概率潮流问题的主要步骤。
第一步:通过式(13)获得N=2n+1个采样点。
第二步:计算每个Sigma采样点的均值权重和协方差权重。
第三步:基于以下步骤将每个采样点馈送到非线性函数式(14)中。
Step1:生成Xi的随机向量。向量Xi包括配电网中网络参数、DG和PEV中随机变量。
Step2:通过非线性方程组f,计算向量Yi。
Step3:以向量Yi作为输入,Xi作为输出,训练RBF。在已经训练好的网络中,当输入向量Y*时在输出处产生向量X*。
Step4:在Step3中训练好的网络中,输入向量Y*产生向量X0。
Step5:将X0代入非线性方程组f求得Y0,将Y0与Y*进行比较。如果‖Y0-Y*‖2满足预定的公差,则算法停止,向量X0将被选择为最优解。否则,进行下一步。
Step6:如果上一步产生的Y0比其他Yi更接近Y*,则(Yi, Xi)中的一个将被替换为(Y0, X0),然后转到Step3。如果约束条件不满足,则用约束条件中的最大值或最小值替换当前参数,并且算法转到步骤Step4。
第四步:按式(15)、式(16)分别计算输出变量Y的均值和协方差。
3.2 基于成功历史的自适应差分进化算法(SHADE)标准的差分进化算法有4个基本步骤:初始化、变异、交叉和选择,SHADE使用了被个体成功使用控制参数的历史存储器M来指导变异和交叉中控制参数值的选择[15]。每一代成功产生比父代个体好的试验向量的交叉率CR和放缩因子F记为SCR、SF,他们的平均值存储在历史存储器MCR、MF中。如表 1所示,SHADE保留H条参数,以便在搜索过程中引导控制参数实现自适应,按照式(21)、式(22)更新历史存储器M。即使某些子代的SCR、SF含有一组较差的值,存储在前一代存储器中的参数也不会受到影响。因此,基于成功历史参数的自适应策略提高了算法的鲁棒性,能够加快算法的收敛速度。
| 表 1 控制参数历史存储器M Table 1 History memory M of the control parameter |
| $ {M_{CR,t + 1}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{\rm{M}}_{{\rm{WA}}}}\left( {{S_{{\rm{CR}}}}} \right)}&{{S_{{\rm{CR}}}} \ne \emptyset ,} \end{array}}\\ {\begin{array}{*{20}{c}} {{M_{CR,t}}}&{其他,} \end{array}} \end{array}} \right. $ | (21) |
| $ {M_{F,t + 1}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{\rm{M}}_{WL}}\left( {{S_F}} \right)}&{{S_F} \ne \emptyset ,} \end{array}}\\ {\begin{array}{*{20}{c}} {{M_{F,t}}}&{其他,} \end{array}} \end{array}} \right. $ | (22) |
式中MWA(SCR)和MWL(SF)分别表示SCR的权重均值和SF的权重Lehmer均值。初始化索引k=1,每当有一对新的SCR和SF插入到存储器时,索引k=k+1。当在t代所有个体都不能产生比父代更好的试验向量时,存储器不更新。
在每一代中,每个个体进行交叉和变异操作之前,控制参数CR和F首先从[1,H]随机选择,然后应用公式(21)、式(22)求得其控制参数CR、F。
| $ C{R_i} = {\rm{rand}}{n_i}\left( {{M_{{\rm{CR}}}},0.1} \right), $ | (23) |
| $ {F_i} = {\rm{rand}}{c_i}\left( {{M_F},0.1} \right), $ | (24) |
式中:randci(MF, 0.1)表示生成一个服从以MF为位置参数,以0.1为尺度参数的Cauchy分布的值;randni(MCR, 0.1)表示生成一个服从均值为MCR,标准差为0.1的正态分布的值。如果CR,F生成的值超出范围[0, 1],按照JADE的参数自适应调整方式[16]。
3.3 UT(RBF)与SHADE算法求解步骤1) 初始化算法。设定种群规模Np、最大进化代数Tmax、决策变量维数d以及配电网基本参数和UT(RBF)算法基本参数。
2) 对目标向量Xit进行交叉和变异操作。采用“current-to-pbest/1”变异策略,生成变异向量Vit;采用二项式交叉,每当0和1之间随机生成的数字小于或等于交叉率CR时,变异向量Vit和目标向量Xit交叉,生成试验向量Uit。
3) 根据UT(RBF)算法对目标向量Xit和试验向量Uit进行概率潮流计算,计算目标函数值和适应度。
4) 根据贪婪算法进行选择操作。如果试验向量Uit的适应度优于目标向量Xit,则在下一代中试验向量Uit取代目标向量Xit,并更新存储器MCR、MF的值;否则目标向量Xit被保存,存储器不更新。
5) 停止标准。判断是否达到最大进化代数Tmax。如果是,则停止并输出最优解。如果不是,转到步骤2)。
4 仿真结果及分析 4.1 参数设置笔者以IEEE33节点配电系统为例,网络结构参数参考文献[17]。该配电系统共有33个节点,节点1为发电机节点。DG和PEV通过恒功率因数控制方式并网,成本参数见表 2,候选节点综合考虑资源分布和节点电压幅值[7]。
| 表 2 DG与PEV成本参数 Table 2 Cost parameters of the DG and PEV |
WG概率模型中风速v服从k=2.1、c=7.5的Weibull分布,功率因数为0.95,候选节点为6,10,17,18;PV概率模型中太阳辐射r服从α=0.3、β=1.2的Beta分布,功率因数为1,候选节点为6,9,18,28。其中假设该区域的电动汽车有400辆,均匀分布在各配电区,行驶起始时间T服从μT=17.6、σT=3.8的正态分布,日行驶里程d服从μd=3.2、σd=0.88的对数正态分布,功率因数为0.9,候选节点为6,28。
4.2 优化结果分析初始化SHADE参数设置,群体规模Np为200,最大迭代次数为500,存储器大小H=7,初始化CR=F=0.5。SHADE采用并行计算的方式处理本文多目标优化问题。通过仿真所得优化配置结果如表 3所示。
| 表 3 优化配置结果 Table 3 Results of optimal configuration |
将DE-MCS、QPSO-CLMCS与上述提出的SHADE-UT(RBF)方法在对DG和PEV优化配置的问题上进行对比。其中3种算法的种群规模均取200,最大迭代次数为500,CLMCS采样次数为500,且3种算法均采用相同的机会约束以及不等式约束。分别计算3种方法在规划期内目标函数最优值,通过Matlab仿真得到的最优目标函数值如表 4所示。
| 表 4 3种方法最优目标函数值 Table 4 Three methods the optimal objective function value |
通过对比表 3所示DG总费用、缺供电量成本以及有功损耗费用,DE-MCS所求得的目标函数值在3种算法中最高,这是因为在DE算法求解过程中,进化代数的增加,会使种群的多样性变小,过早的收敛到局部极小点。QPSO-CLMCS将量子粒子群与拉丁超立方采样蒙特卡洛方法相结合,但是在搜索后期,粒子聚集成群导致搜索空间变得有限。在3种优化算法中SHADE-UT(RBF)目标函数值最低,优化结果最好。总目标函数值对比DE-MCS和QPSO-CLMCS分别减少了36.5%、11.2%。并且3种方法的计算时间分别为DE-MCS 14 min、QPSO-CLMCS 10 min和SHADE-UT(RBF) 3 min,SHADE-UT(RBF)在3种方法中用时最短,这是因为UT(RBF)对比CLMCS避免了蒙特卡洛模拟计算负担重的缺陷,舍弃了传统计算潮流的方法,避免了计算雅可比矩阵。SHADE采用基于成功历史参数自适应算法,将成功的历史记录储存在寄存器中,加速了算法收敛速度。仿真结果表明,在DG和PEV优化配置问题上,SHADE-UT(RBF)能更好地保证电网运行的经济性与可靠性。
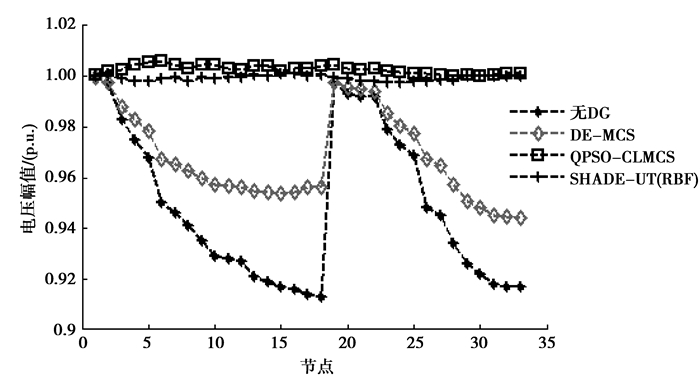
4.3 电压水平分析为了分析不同算法对系统节点电压的影响,3种算法优化后的节点电压结果以及不安装DG时节点电压水平如图 1所示。
|
图 1 节点电压水平 Figure 1 Node voltage level |
未接入DG时,节点电压严重超出电压允许上下偏移量0.95~1.05 p.u.。在接入DG后,3种方法均能使节点电压幅值得到较大改善,但DE-MCS由于容易过早收敛,导致仍有少量节点未能达电压允许偏移量。QPSO-CLMCS和SHADE-UT(RBF)所求得电压均在允许的偏移量内,但不难看出SHADE-UT(RBF)的优化效果更好,大部分节点电压幅值在1 p.u.,提高了供电安全性和可靠性。
5 结语将概率潮流计算引入SHADE求得最优规划方案。采用UT和RBF相结合的方式求解含DG和PEV的概率潮流,充分考虑DG和PEV的间歇性、随机性和相关性。采用SHADE求解多目标优化问题,以DG总费用、供电可靠性和有功损耗为目标函数,更能反映实际需要。SHADE能够快速地收敛到全局最优解,避免了传统差分进化算法容易过早收敛的缺陷。本研究通过仿真验证了所提算法能够在保证计算精度的同时快速收敛,满足实际工程要求,降低了节点电压的波动以及优化成本,同时为大规模PEV和DG并网提供了可靠的理论依据。
| [1] |
谢维兵, 刘敏, 周晓霞, 等. 含电压逆变型分布式电源配电网的短路电流计算[J]. 重庆大学学报, 2017, 40(2): 70-79. XIE Weibing, LIU Min, ZHOU Xiaoxia, et al. Short-circuit current calculation of distributed power distribution network with voltage inverter[J]. Journal of Chongqing University, 2017, 40(2): 70-79. (in Chinese) |
| [2] |
周湶, 曹立平, 李剑, 等. 改进遗传算法在分布式电源选址定容中的应用[J]. 重庆大学学报, 2014, 37(5): 22-28. ZHOU Wei, CAO Liping, LI Jian, et al. Application of improved genetic algorithm in distributed power source location and volume[J]. Journal of Chongqing University, 2014, 37(5): 22-28. (in Chinese) |
| [3] |
熊强, 陈维荣, 张雪霞, 等. 考虑多风电场相关性的场景概率潮流计算[J]. 电网技术, 2015, 39(8): 2154-2159. XIONG Qiang, CHEN Weirong, ZHANG Xuexia, et al. Calculation of probability power flow in scenarios considering the correlation of wind farms[J]. Power System Technology, 2015, 39(8): 2154-2159. (in Chinese) |
| [4] |
代景龙, 韦化, 鲍海波, 等. 基于无迹变换含分布式电源系统的随机潮流[J]. 电力自动化设备, 2016, 36(3): 86-93. DAI Jinglong, WEI Hua, BAO Haibo, et al. Stochastic power flow based distributed distributed power system with no trace transform[J]. Electric Power Automation Equipment, 2016, 36(3): 86-93. (in Chinese) |
| [5] |
Baghaee H R, Mirsalim M, Gharehpetian G B, et al. Application of RBF neural networks and unscented transformation in probabilistic power-flow of microgrids including correlated wind/PV units and plug-in hybrid electric vehicles[J]. Simulation Modelling Practice & Theory, 2017, 72(C): 51-68. |
| [6] |
刘文霞, 徐慧婷. 考虑电压控制成本的分布式电源优化配置[J]. 电网技术, 2016, 40(10): 2998-3005. LIU Wenxia, XU Huiting. Distributed power supply optimal configuration considering voltage control cost[J]. Power System Technology, 2016, 40(10): 2998-3005. (in Chinese) |
| [7] |
彭显刚, 林利祥, 刘艺, 等. 计及电动汽车和可再生能源不确定因素的多目标分布式电源优化配置[J]. 电网技术, 2015, 39(8): 2188-2194. PENG Xiangang, LIN Lixiang, LIU Yi, et al. Optimization of multi-objective distributed generation considering electric vehicles and uncertainties of renewable energy[J]. Power System Technology, 2015, 39(8): 2188-2194. (in Chinese) |
| [8] |
盛万兴, 叶学顺, 刘科研, 等. 基于NSGA-Ⅱ算法的分布式电源与微电网分组优化配置[J]. 中国电机工程学报, 2015, 35(18): 4655-4662. SHENG Wanxing, YE Xueshun, LIU Keyan, et al. Optimized allocation of DGs and microgrids based on NSGA-Ⅱ algorithm[J]. Proceeding of the CSEE, 2015, 35(18): 4655-4662. (in Chinese) |
| [9] |
周辛南, 柯德平, 孙元章. 基于配电网静态电压质量机会性约束的可再生能源分布式发电容量规划[J]. 电力自动化设备, 2015, 35(9): 143-149. ZHOU Xinnan, KE Deping, SUN Yuanzhang. Distributed energy generation capacity planning based on chance constraints of static voltage quality in distribution network[J]. Electric Power Automation Equipment, 2015, 35(9): 143-149. (in Chinese) |
| [10] |
吕智林, 谭颖, 李捷, 等. 基于Markov-ELM的独立混合微网分布式电源多目标容量优化配置[J]. 中国电机工程学报, 2017(7): 1927-1936. LV Zhilin, TAN Ying, LI Jie, et al. Multi-objective capacity optimization of independent hybrid micro-grid distributed generation based on Markov-ELM[J]. Proceedings of the CSEE, 2017(7): 1927-1936. (in Chinese) |
| [11] |
蔡德福, 钱斌, 陈金富, 等. 含电动汽车充电负荷和风电的电力系统动态概率特性分析[J]. 电网技术, 2013, 37(3): 590-596. CAI Defu, QIAN Bin, CHEN Jinfu, et al. Analysis on dynamic probabilistic characteristics of power system with electric vehicle charging load and wind power[J]. Power System Technology, 2013, 37(3): 590-596. (in Chinese) |
| [12] |
彭显刚, 林利祥, 刘艺, 等. 基于纵横交叉[XC半字线.TIF, JZ]拉丁超立方采样蒙特卡洛模拟法的分布式电源优化配置[J]. 中国电机工程学报, 2015, 35(16): 4077-4085. PENG Xiangang, LIN Lixiang, LIU Yi, et al. Optimal distributed generator allocation method based on correlation latin hypercube sampling monte carlo simulation embedded crisscross optimization algorithm[J]. Proceedings of the CSEE, 2015, 35(16): 4077-4085. (in Chinese) |
| [13] |
Aien M, Rashidinejad M, Firuz-Abad M F. Probabilistic optimal power flow in correlated hybrid wind-PV power systems:A review and a new approach[J]. Renewable and Sustainable Energy Reviews, 2015, 41: 1437-1446. DOI:10.1016/j.rser.2014.09.012 |
| [14] |
Zimmerman R D, Murillo-Sanchez C E, Thomas R J. MATPOWER's extensible optimal power flow architecture[C]//Power & Energy Society General Meeting, 2009. PES'09. IEEE. IEEE, 2009: 1-7.
|
| [15] |
Tanabe R, Fukunaga A. Success-history based parameter adaptation for Differential Evolution[C]//Evolutionary Computation. IEEE, 2013: 71-78.
|
| [16] |
Zhang J, Sanderson A C. JADE:Adaptive differential evolution with optional external archive[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958. DOI:10.1109/TEVC.2009.2014613 |
| [17] |
Demuth H, Beale M. Neural network toolbox-for use with mATLAB[J]. Matlab Users Guide the Math Works, 1995, 21(15): 1225-1233. |
 2018, Vol. 41
2018, Vol. 41

