2. 重庆齿轮箱有限责任公司, 重庆 402263
2. CN GPower Gearbox Co., Ltd., Chongqing 402263, P. R. China
随着中国海洋钻探技术的发展,海洋工程装备水平得到了快速提高,升降齿轮箱作为海洋工程平台的重要组成部分,正朝着大功率、高可靠和低振动等方向发展,其机械性能及动力学特性备受关注[1-2]。为设计大传动比且结构紧凑的提升装置,多级行星齿轮传动在升降齿轮箱中被广泛应用,但在恶劣的近海环境作业时,海洋平台可能因齿轮箱的内部激励作用引发剧烈振动,有必要对其振动噪声进行预估和试验研究。
行星齿轮传动系统的动力学问题一直是国内外学术研究的重点[3],其振动响应分析方法包括集中参数法[4]、有限元法[5]或将两种方法综合运用[6-7]。齿轮箱振动分析通常采用动力有限元法,通过耦合冲击、误差、刚度等内部激励[8],基于数值方法计算齿轮箱的动态响应;齿轮箱辐射噪声预估通常以振动响应为边界条件,利用声学边界元法求解辐射噪声[9-10],而振动噪声测试可以对仿真结果进行验证[11]。轮齿修形是一种有效的减振降噪方法[12],可以缓解齿轮副因热弹变形引起的啮合冲击,改善齿轮副的动态啮合性能[13],但目前相关研究中较少涉及基于轮齿修形的多级行星齿轮箱减振降噪计算方法,因此有必要对多级行星齿轮箱进行振动噪声预估及修形效果分析。
笔者以海洋平台升降齿轮箱的4级行星齿轮传动系统为研究对象,在计算齿轮箱固有振动模态和齿轮副内部动态激励的基础上,采用模态叠加法对修形前后齿轮箱进行振动响应有限元分析,将求得的齿轮箱振动响应作为边界条件,利用直接边界元法对箱体的辐射噪声进行计算,而后搭建升降齿轮箱振动噪声试验台进行振动噪声测试。
1 4级行星齿轮箱振动模态分析 1.1 传动系统结构形式海洋平台升降齿轮箱采用4级NGW型行星齿轮传动,各级传动均采用直齿圆柱齿轮,行星轮数为3,齿轮副参数如表 1所示。
| 表 1 齿轮传动系统主要参数 Table 1 Main parameters of gear transmission system |
利用Romax软件建立包含齿轮、轴和轴承的4级行星传动系统三维实体模型,如图 1所示,各行星级中太阳轮为输入部件,行星架为输出部件,内齿圈与箱体固接。功率由1级太阳轮输入,经1级行星架传递到2级太阳轮,再经第2级、第3级行星轮系传递到第4级行星轮系,由4级行星架输出并驱动输出齿轮轴,输出齿轮轴与齿条啮合实现升降运动。齿轮传动系统中除行星轴上的轴承外,仅1级太阳轮、4级行星架和输出齿轮轴上存在与箱体接触的轴承,各级太阳轮及行星架均浮动。将齿轮齿条啮合副的受力转化为力和转矩施加到输出齿轮轴上,对4级行星传动系统进行静力分析,并提取轴承的支撑刚度[10]。

|
图 1 Romax中传动系统实体模型 Figure 1 Solid model of transmission system in Romax software |
利用ANSYS软件建立包含箱体、齿轮副、传动轴、行星架和轴承的耦合系统模态分析模型,由弹簧单元模拟齿轮副接触刚度和轴承支撑刚度,升降齿轮箱有限元网格如图 2所示,共计298 359个单元,22 7587个节点。采用分块Lanczos法对齿轮箱进行振动模态分析,得出齿轮箱各阶固有频率和振型,如表 2所示,图 3给出了第1阶固有振型。

|
图 2 齿轮箱振动模态分析有限元模型 Figure 2 Finite element model of gearbox for mode analysis |
| 表 2 前10阶固有振动频率及振型 Table 2 The first 10 natural frequencies and its mode |
|
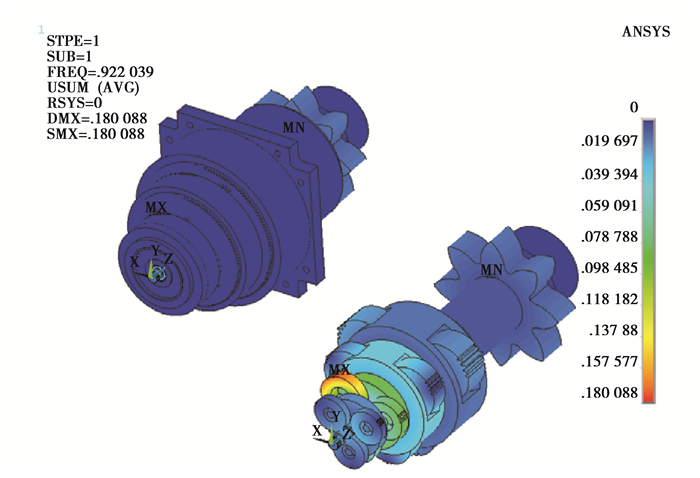
图 3 齿轮箱第1阶固有振型 Figure 3 The 1st order vibration mode of gearbox |
由表 2可知,4级行星齿轮传动系统中各部件之间相互作用,振动模式较为丰富。升降齿轮箱的转频与啮合频率等激励频率与固有频率的接近率均大于10%,不会与固有频率合拍,齿轮箱共振的可能性较小。
2 4级行星齿轮箱振动响应分析 2.1 齿轮系统内部动态激励升降齿轮箱内部动态激励主要包括刚度激励、误差激励和啮合冲击激励[10, 14],其表达式为
| $ F\left( t \right) = \Delta k\left( t \right)e\left( t \right) + S\left( t \right), $ | (1) |
式中:F(t)为内部动态激励;Δk(t)为啮合刚度的变刚度部分;e(t)为齿轮综合误差;S(t)为啮合冲击激励。
齿轮副通过适当修形,由热弹变形或偏载引起的异常啮合情况将得到改善,冲击激励明显减小,刚度激励也会发生改变。文中修形参数根据额定工况下齿轮的热弹变形计算得到,太阳轮和行星轮的齿顶修缘参数如表 3所示。
| 表 3 齿轮箱齿廓修形参数 Table 3 Parameters of tooth profile modification for gearbox |
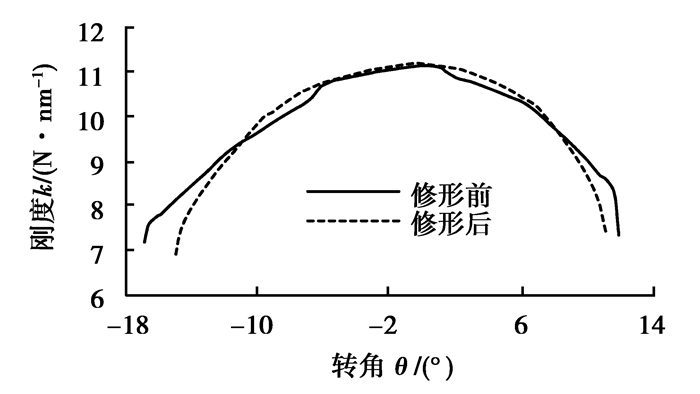
基于含修形量的齿廓坐标建立齿轮副模型,利用接触有限元法求解修形前后齿轮副啮合过程中的轮齿接触力和齿面变形,计算可得齿轮副啮合刚度。图 4给出了修形前后第1级行星轮系外啮合齿轮副的单齿啮合刚度曲线。由图 4可知,在啮入和啮出位置,修形后齿轮副的单齿啮合刚度降低,单齿接触对应的转角范围也有所减小,齿轮副提前进入啮合和滞后退出啮合现象得到改善。
|
图 4 修形前后单齿啮合刚度曲线 Figure 4 The single tooth meshing stiffness curve before and after modification |
轮齿综合误差主要由基节误差和齿形误差组成,可用简谐函数表示。若太阳轮和行星轮的精度为5级,齿圈的精度为6级,则1~4级外啮合齿轮副齿轮误差幅值分别为7.9, 11.1, 19.0, 20.0 μm,相应的内啮合齿轮副误差幅值分别为12.5, 14.0, 19.0, 20.0 μm。
修形后齿轮副冲击激励和刚度激励将发生变化,其中啮合冲击激励大幅减小。若忽略冲击激励,则内部动态激励可表示为
| $ F'\left( t \right) = \Delta k'\left( t \right)e\left( t \right), $ | (2) |
式中:F′(t)为修形后的内部动态激励;Δk′(t)为修形后啮合刚度的变刚度部分。
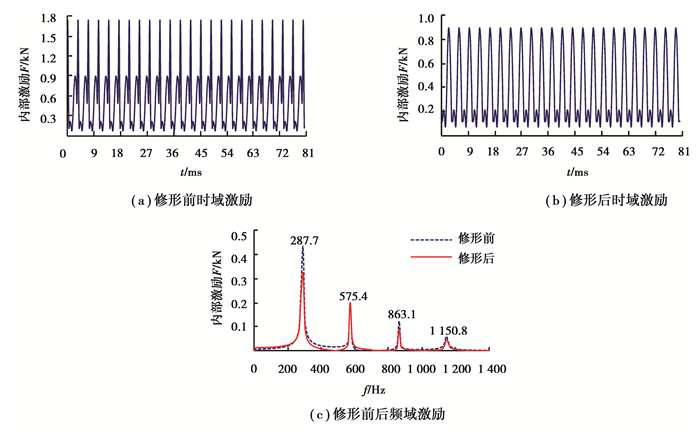
在额定工况为输入转速980 r/min、输入功率23 kW时,采用三维冲击动力接触有限元混合法计算各齿轮副的啮合冲击激励[8]。图 5给出了修形前后第1级行星轮系外啮合齿轮副的内部动态激励曲线,由图可知,修形后齿轮副的内部动态激励明显降低。
|
图 5 齿轮副内部动态激励 Figure 5 The internal dynamic excitation of gear pair |
4级行星齿轮箱内部动态激励中,同级行星轮系外啮合和内啮合齿轮副之间可能存在相位差,3个行星轮之间也可能存在相位差[15],因此在施加激励时,须考虑各齿轮副实际相位情况。
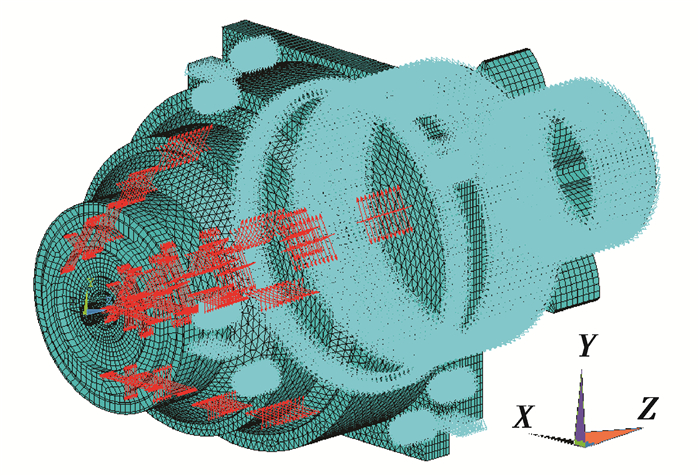
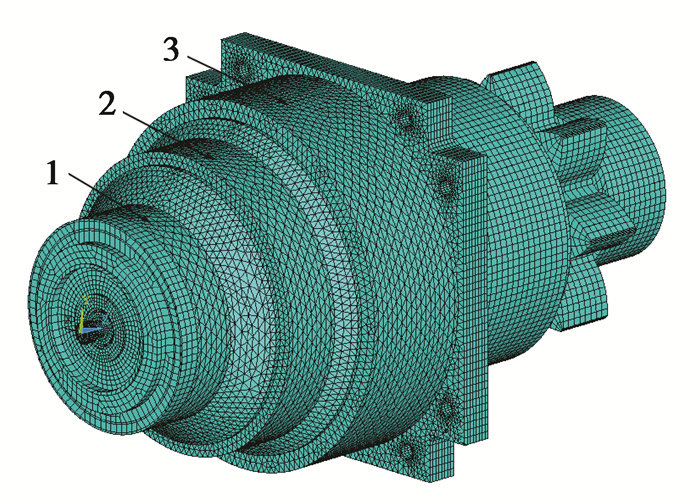
2.2 齿轮箱振动响应分析4级行星齿轮箱模型较大且结构复杂,采用模态叠加法可以较快速地计算得到内部动态激励作用下系统的振动位移、振动速度和振动加速度响应。将额定工况下各级齿轮副的内部动态激励按切向和径向分力分别施加到齿面的啮合位置,并在基座螺栓孔、安装圆筒及输出齿轮轴端部轴承外圈处施加固定约束,基座台肩处施加Y向位移约束,图 6给出了齿轮箱振动响应计算模型。选取齿轮箱表面齿圈部位处的3个节点为振动响应评价点,如图 7所示。
|
图 6 齿轮箱振动响应有限元模型 Figure 6 Finite element model of gearbox for vibration response |
|
图 7 齿轮箱振动响应评价点位置 Figure 7 Assessment points for vibration response of gearbox |
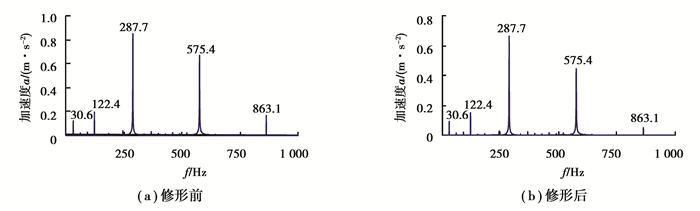
图 8给出了修形前后4级行星齿轮箱评价点1的X向振动加速度频域响应曲线。修形前后振动响应的峰值频率较为一致,主要出现在863.1,575.4,287.7,122.4和30.6 Hz,均为啮合频率或其倍频,修形前的振动加速度最大峰值为0.846 m/s2,出现在287.7 Hz处,修形后减小到0.66 m/s2。
|
图 8 齿轮箱振动加速度频域曲线 Figure 8 Vibration acceleration response in frequency domain of gearbox |
振动响应的有效值可通过计算时域响应的均方根得到[16]:
| $ {a_{{\rm{rms}}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {a_i^2} } {\rm{,}} $ | (3) |
式中:N为响应数据点数;ai为第i个数据的值。
表 4给出了修形前后各评价点X, Y, Z向振动加速度的有效值。由表可知,由于评价点1位于1级内齿圈处,处于最高转速部位且远离固定端,该点处的振动加速度响应较大;评价点3离固定端较近,振动加速度响应最小。修形后升降齿轮箱振动加速度响应明显降低,其最大有效值由修形前的3.143 m/s2减小到2.584 m/s2,减少了17.8%。
| 表 4 齿轮箱振动加速度有效值 Table 4 The RMS values of vibration acceleration of gearbox |
声学计算方法主要分为声学有限元法(FEM)和声学边界元法(BEM)法,笔者在SYSNOISE中利用直接边界元法求解表面声压。建立4级行星齿轮箱箱体外表面的封闭有限元网格模型,共计17 704个节点,25 396个单元,将模型导入SYSNOISE得到齿轮箱声学边界元模型,如图 9所示。

|
图 9 齿轮箱声学边界元模型 Figure 9 Acoustic boundary element model of gearbox |
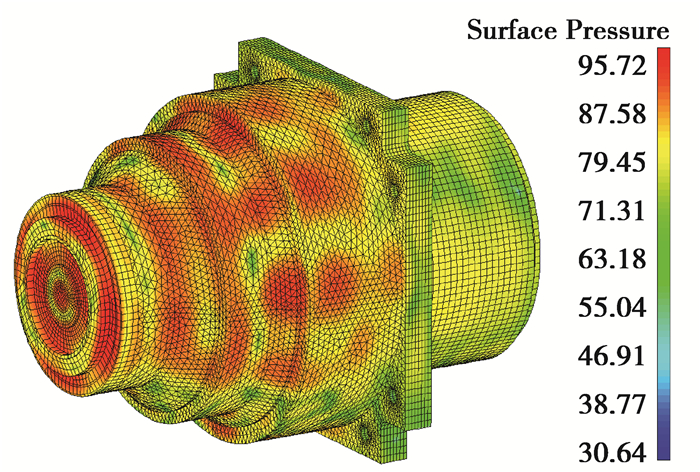
4级行星齿轮箱辐射噪声仿真时,设置空气密度为1.225 kg/m3,声速为340 m/s,参考声压为2×10-5 Pa,计算时频率按倍频程设定,频率范围从31.5 Hz到4 000 Hz。以箱体表面节点的频域响应为边界条件,计算可得各频段箱体表面的基本声学量。升降齿轮箱表面声压的最大值出现在3级内齿圈附近,其值为95.72 dB,位于2 kHz频段,此时的箱体表面声压如图 10所示。
|
图 10 齿轮箱表面声压云图 Figure 10 The surface sound pressure contour of gearbox |
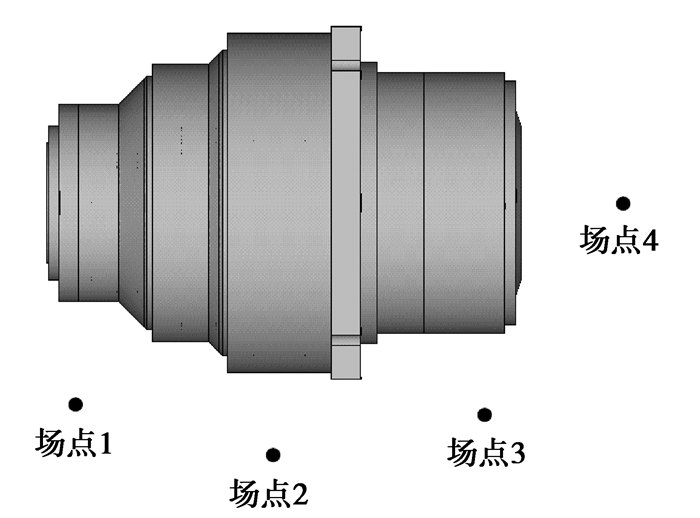
在距齿轮箱表面1 m处设置如图 11所示的4个场点,计算场点1~4在各频段的A计权倍频程声压级辐射噪声,表 5给出了修形前后各场点的辐射噪声声压级。
|
图 11 齿轮箱场点俯视图 Figure 11 The top view of gearbox field points |
| 表 5 齿轮箱各场点的辐射噪声 Table 5 Radiation noise of gearbox field points |
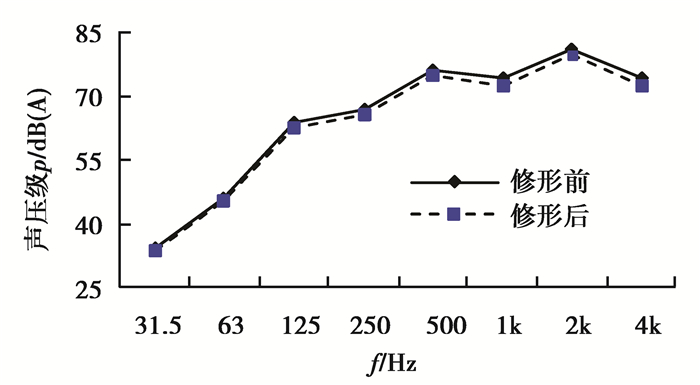
由表可知,修形前齿轮箱各场点辐射噪声最大值为83.3 dB(A),出现在场点2处,修形后减小为81.8 dB(A),且各场点辐射噪声结果均有所减小。图 12给出了修形前后场点2的声压级频响曲线,最大值均位于2 kHz处。
|
图 12 场点2的声压级频响曲线 Figure 12 The sound pressure in frequency domain of field point 2 |
搭建修形后齿轮箱的振动噪声测试台架,齿轮箱左、右机同时与试验齿条啮合,其中左机拖动,右机加载,试验台如图 13所示。左、右机减速器在靠近4级齿圈的壳体端面采用螺栓与机架固定,并在齿轮箱底部台肩处采用垫块支撑,对额定工况运行时的齿轮箱进行振动噪声测试。

|
图 13 升降齿轮箱试验台架 Figure 13 Test bench of lifting gearbox |
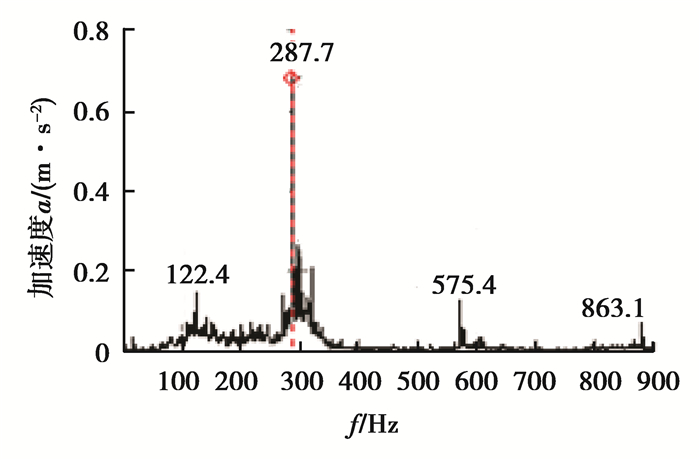
利用BK4384加速度传感器采集4级行星齿轮箱3个评价点的X,Y,Z向振动加速度。图 14给出了评价点1的X向振动加速度测试结果的频域曲线,对比图 8(b)可知,仿真与测试得到的齿轮箱振动加速度频域曲线较为一致,其峰值均出现在齿轮啮合频率或其倍频处。表 6给出了各评价点振动加速度测试结果的有效值,对比表 4可知,振动加速度仿真和测试结果吻合良好。
|
图 14 实测振动加速度频域曲线 Figure 14 Test curve of vibration acceleration in frequency domain |
| 表 6 振动加速度测试结果有效值 Table 6 Test RMS values of vibration acceleration |
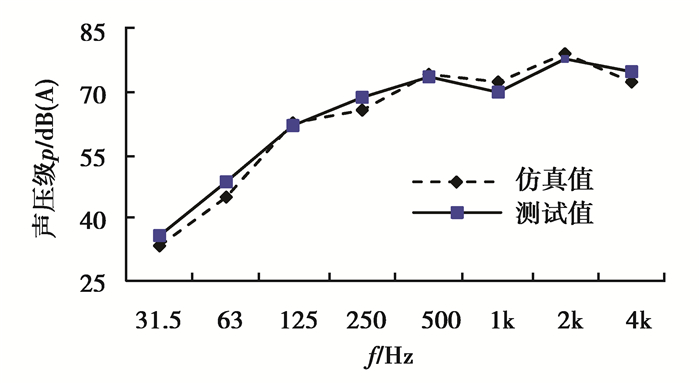
利用NL-42型声级计采集4级行星齿轮箱在4个场点的总声压级。各场点的总声压级如表 7所示。由表可知,齿轮箱实测总声压级最大值为81.4dB(A),位于场点2处,测试与仿真所得的总声压级最大值相差0.49%,各场点总声压级的相对误差最大值为3.64%,仿真与测试结果吻合良好。图 15给出了场点2处测试和计算所得的声压级频响曲线。
| 表 7 场点的总声压级 Table 7 Total sound pressure level of field points |
|
图 15 声压级频响曲线 Figure 15 The sound pressure in frequency domain |
1) 利用Romax软件求解轴承刚度,在ANSYS中建立了包含行星轮系、轴承和箱体的齿轮箱有限元模型,通过基于Lanczos法的振动模态分析,得出齿轮箱额定转速下发生共振的可能性较小。
2) 计算了修形前后齿轮副的内部动态激励,采用模态叠加法求解了4级行星齿轮箱的振动响应,修形后齿轮箱各评价点中最大振动加速度有效值减小了17.8%。
3) 采用直接边界元法求解了修形前后齿轮箱的辐射噪声,修形后各场点辐射噪声最大值减小了1.5 dB(A),修形对升降齿轮箱的减振降噪效果较为明显。
4) 利用升降齿轮箱试验台架进行振动噪声测试,实测振动加速度和辐射噪声与仿真结果吻合良好,表明提出的含轮齿修形的行星齿轮箱振动噪声预估方法的合理性。
| [1] |
蒋晓宁. 自升式海洋钻探平台开发设计研究[D]. 大连: 大连海洋大学, 2015. JIANG Xiaoning. The research and development of jack-up drilling platform[D]. Dalian: Dalian Maritime University, 2015. (in Chinese) |
| [2] | Cassidy M J. Offshore foundation systems for resource recovery:Assessing the three-dimensional response of jack-up platforms[J]. KSCE Journal of Civil Engineering, 2011, 15(4): 623–634. DOI:10.1007/s12205-011-0003-9 |
| [3] |
卜忠红, 刘更, 吴立言.
行星齿轮传动动力学研究进展[J]. 振动与冲击, 2010, 29(9): 161–166.
BU Zhonghong, LIU Geng, WU Liyan. Research advances in planetary gear trains dynamics[J]. Journal of Vibration and Shock, 2010, 29(9): 161–166. (in Chinese) |
| [4] | ZHANG L, Wang Y, Wu K, et al. Dynamic modeling and vibration characteristics of a two-stage closed-form planetary gear train[J]. Mechanism and Machine Theory, 2016, 97: 12–28. DOI:10.1016/j.mechmachtheory.2015.10.006 |
| [5] | Zeng W, Zhu X Z, Wei Z J. Study on nonlinear dynamic response of the gear-shaft-housing coupling system[J]. Applied Mechanics and Materials, 2010(26/27/28): 805–808. |
| [6] | Abousleiman V, Velex P. A hybrid 3D finite element/lumped parameter model for quasi-static and dynamic analyses of planetary/epicyclic gear sets[J]. Mechanism & Machine Theory, 2006, 41(6): 725–748. |
| [7] |
贺朝霞, 常乐浩, 刘岚.
耦合箱体振动的行星齿轮传动系统动态响应分析[J]. 华南理工大学学报(自然科学版), 2015, 43(9): 128–134, 148.
HE Zhaoxia, CHANG Lehao, LIU Lan. Dynamic response analysis of planetary gear transmission system coupled with gearbox vibrations[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(9): 128–134, 148. (in Chinese) |
| [8] | Lin T, Ou H, Li R. A finite element method for 3D static and dynamic contact/impact analysis of gear drives[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(9): 1716–1728. |
| [9] |
吴飞. 汽车车身振动噪音控制混合数值方法研究[D]. 长沙: 湖南大学, 2015. WU Fei. The research of hybrid numerical methods for control of vibration and noise of vehicle boby structure[D]. Changsha: Hunan University, 2015. (in Chinese) |
| [10] |
林腾蛟, 郭进, 刘波, 等.
风电增速箱结合部刚度分析及振动噪声预估[J]. 重庆大学学报(自然科学版), 2015, 38(1): 87–94.
LIN Tengjiao, GUO Jin, LIU Bo, et al. Junction stiffness analysis and vibration noise prediction of wind power speed-increase gearbox[J]. Journal of Chongqing University (Natural Science Edition), 2015, 38(1): 87–94. (in Chinese) |
| [11] |
石万凯, 郑站强, 李学明.
风电齿轮箱动态响应分析及实验测量[J]. 机械设计, 2012, 29(4): 63–68.
SHI Wankai, ZHENG Zhanqiang, LI Xueming. Dynamic response analysis and experimental measurements of wind turbine gearbox[J]. Journal of Machine Design, 2012, 29(4): 63–68. (in Chinese) |
| [12] | Chen Z, Shao Y. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism and Machine Theory, 2013, 62: 63–74. DOI:10.1016/j.mechmachtheory.2012.10.012 |
| [13] |
姚阳迪. 基于热弹变形的高速重载齿轮修形研究[D]. 重庆: 重庆大学, 2010. YAO Yangdi. Modification research of high-speed and heavy-load gear based on thermo-elastic deformation[D]. Chongqing: Chongqing University, 2010. (in Chinese) |
| [14] | Ajmi M, Velex P. A model for simulating the quasi-static and dynamic behaviour of solid wide-faced spur and helical gears[J]. Mechanism & Machine Theory, 2005, 40(2): 173–190. |
| [15] |
肖正明, 秦大同, 尹志宏.
多级行星齿轮系统耦合动力学分析与试验研究[J]. 机械工程学报, 2012, 48(23): 51–58.
XIAO Zhengming, QIN Datong, YIN Zhihong. Multi-stage planetary gears dynamic coupling analysis and experimental investigation[J]. Chinese Journal of Mechanical Engineering, 2012, 48(23): 51–58. (in Chinese) |
| [16] |
戴诗亮. 随机振动实验技术[M]. 清华大学出版社, 1984.
DAI Shiliang. Experimental techniques of random vibration[M]. Tsinghua University Press, 1984. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41

