数控机床是集机、电、液、控等多学科领域的复杂产品,更是装备制造业的“工作母机”。自国家“高档数控机床与基础制造装备”科技重大专项实施以来,中国数控机床的技术水平得到长足发展,数控机床质量水平显著提高。质量是数控机床的核心,一旦数控机床因质量问题停机中断生产,将会给企业造成重大损失。因此,在企业和客户决策之前对数控机床质量进行综合评价显得尤为重要。
评价过程的核心是如何确定评价指标的相对重要程度即权重。文献[1]运用层次分析法、熵权法和均方差法计算电能质量各项指标的综合权重,提出了基于可拓云理论的电能质量评估数学模型;文献[2]采用模糊层次分析法提出了基于模糊物元的绿色产品评价方法;文献[3]将疲劳累积损伤理论和雨流计数法引入物元模型,结合层次分析法确定可靠性各等级的评价权重,提出了高速轨道车辆传动系可靠性评价的物元模型;文献[4]基于质量功能配置(quality function deployment, QFD)构建了产品再制造质量特性评价模型;文献[5]综合运用模糊数据包络分析法和QFD评价产品设计质量;文献[6]提出了基于数据包络分析法、主成分分析法和数值分类法的质量评价方法;文献[7]构建了燃煤机组节能减排性能评价指标体系,将最大熵与PP结合用于评价燃煤机组节能减排性能;文献[8]根据PP原理并结合遗传算法建立了火电机组可靠性评价模型;文献[9]运用遗传算法对PP指标进行了优化并取得了一定成果。
综上所述,关于质量评价方法目前主要有可拓云模型(extension cloud model, ECM)、QFD、物元(matter element, ME)以及模糊物元(fuzzy matter element, FME)分析法等。这些方法在确定评价指标的权重时,从主观方面或客观方面确定评价指标的权重。主观权重考虑了评价指标的价值量,但受主观因素影响较大;客观权重体现了指标信息量,但没有考虑实际情况,使得计算结果可能与实际情况不符。此外,当评价指标数过多时,运用可拓云模型、模糊物元分析法的评价过程较为繁琐,而求解PP投影方向的遗传算法容易陷入局部最优解,算法稳健性较差。为了充分利用主客观权重的优点,使评价过程全面、科学,并在评价指标呈现多维性的情况下简化评价过程,笔者结合基于SCA(sine cosine algorithm)的PP模型与AHP综合评价机床质量:引入SCA计算PP的最佳投影方向,将其归一化后作为评价指标的客观权重;利用AHP得到评价指标的主观权重,根据最小信息熵原理得到组合权重,以投影的方式将多维评价指标值转换为一维投影值,全面、科学地评价数控机床的质量。
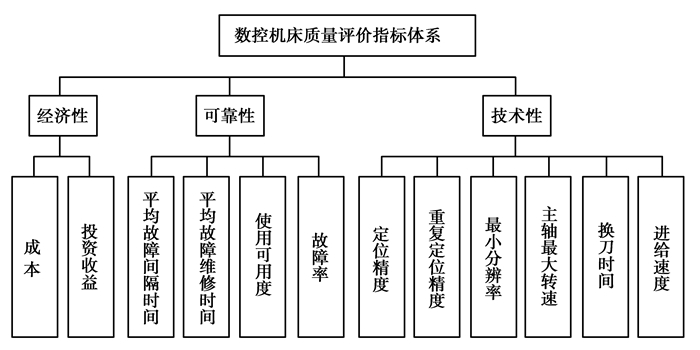
1 数控机床质量评价指标的建立质量表示一组固有属性满足要求的程度。数控机床质量主要是应用质量特性进行描述,是所有质量特性综合结果的体现。评价指标体系建立一般遵循评价的目的性、完整性、科学性和可扩展性等原则, 文献[10]对数控装备质量评价指标进行了全面分析,因此根据文献[10]建立数控机床评价指标体系,如图 1所示。
|
图 1 数控机床质量评价体系 Figure 1 CNC machine tool quality evaluation system |
PP是用来处理和分析高维数据尤其是非正态总体数据的一类统计方法,其基本思想是把高维数据投影到低维子空间上,寻找出能反映高维数据结构或特征的投影,达到简化研究分析高维数据的目的[11]。PP方法的实质是构造一个量化的投影指标函数Q(a),使用数值寻优方法找到最佳投影方向a,将多维指标数据转化为一维投影值z, 从而实现降维分析目的。其具体步骤如下。
1) 样本集的归一化处理。
{x(i, j)|i=1, 2, …, m; j=1, 2, …, n}为样本集,x(i, j)为第i个样本j项指标的实际数值,m,n分别为样本容量和指标个数。为了消除各指标值的量纲,统一各指标值的变化范围,采用式(1)对样本数据进行极值归一化处理。
对于效益型(值越大越优)指标:
| $ {x_b}\left( {i,j} \right) = \frac{{x\left( {i,j} \right) - {x_{{\rm{min}}}}\;\;\left( j \right)}}{{{x_{{\rm{max}}}}\;\;\left( j \right) - {x_{{\rm{min}}}}\;\;\left( j \right)}}。$ | (1) |
对于成本型(值越小越优)指标:
| $ {x_c}\left( {i,j} \right) = \frac{{{x_{{\rm{max}}}}\;\;\left( j \right) - x\left( {i,j} \right)}}{{{x_{{\rm{max}}}}\;\;\left( j \right) - {x_{{\rm{min}}}}\;\;\left( j \right)}}。$ | (2) |
2) 构造投影指标函数。
PP方法就是将n维数据{x(i, j)|i=1, 2, …, m; j=1, 2, …, n}综合成以a = [a1, a2, …,an]为投影方向的一维投影值zi:
| $ {z_i} = \sum\limits_{j = 1}^n {{a_j}{x^*}} \left( {i, j} \right), $ | (3) |
对于效益型指标:x*(i, j)=xb(i, j);对于成本型指标:x*(i, j)=xc(i, j)。确定投影指标时,为了使投影值zi的局部投影点尽可能密集,构造投影指标函数为
| $ Q\left( a \right) = {S_z}{D_z}, $ | (4) |
式中:
| $ {S_z} = \frac{{\sum\limits_{i = 1}^m {\left[{{z_i}-\frac{1}{m}\sum\limits_{i = 1}^m {{z_i}} } \right]} }}{{m -1}}, $ | (5) |
| $ {D_z} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {(R-{r_{ij}})u(R-{r_{ij}}), } } $ | (6) |
Sz为投影值zi的标准差;Dz为投影值z(i)的局部密度; rij= |zi-zj|为样本之间的距离;R为局部密度窗口半径,其值的选取要求窗口包含较多的投影点平均个数,避免滑动平均偏差过大,同时又不能使窗口半径R随样本量m的增大而增加太多[11]。因此R的合理取值范围是rmax+n/2≤R≤2n,其中rmax=max(rij),n为评价指标个数。u(R-rij)为单位阶跃函数,满足:
| $ u(R-{r_{ij}}) = \left\{ \begin{array}{l} 1, \;\;\;\;\;\;\;R-{r_{ij}} \ge 0\\ 0, \;\;\;\;\;\;\;R-{r_{ij}} < 0 \end{array} \right. $ | (7) |
3) 优化投影指标函数。
搜寻最佳投影方向,将搜寻最佳投影方向的问题转化为非线性最优求解问题,即:
| $ \left\{ \begin{array}{l} {\rm{max}}:Q\left( a \right) = {S_z}{D_z}\\ {\rm{s}}{\rm{.t:}}\sum\limits_{j = 1}^n {a_j^2 = 1, {a_j} \in [0, 1]}。\end{array} \right. $ | (8) |
4) 计算投影值。
将最佳投影方向a代入式(3),得到投影值zi。将最佳投影方向归一化后作为评价指标的客观权重,客观权重充分反映了数据结构的特点,并将投影值作为综合评价最终依据。
2.2 SCASCA是澳大利亚学者Seyedali Mirjalili于2015年提出的一种基于正弦余弦函数的新型优化算法。SCA通过创建多个随机候选解,利用正余弦数学公式求解优化问题的最优解。该算法能够探索不同的搜索空间,有效避免局部最优,具有调节参数少、收敛速度快、全局寻优能力强、稳健性好等优点。文献[12]将多峰函数、单峰函数以及混合函数作为测试函数,把粒子群优化算法(particle swarm optimization algorithm, PSOA)、遗传算法(genetic algorithm, GA),蜂群算法(bee colony algorithm, BCA)等6种算法结果与SCA结果作对比,验证了SCA具有良好的稳健性,最后将SCA用于飞机机翼的优化设计并取得了较好的效果。文献[13]将SCA与PP结合,利用SCA求解投影指标函数的最佳投影方向,算出投影值,并将投影值归一化后作为水污染分配的权重,但未考虑水污染分配的主观权重。
以群体为基础的优化算法通过一组随机解以及更新策略不断优化迭代,并利用适应度函数反复评价。在保证足够数的随机解和优化迭代条件下,算法可大大增加获得最优解的概率。SCA的空间位置更新公式如下[12]:
| $ X_i^{t + 1} = \left\{ \begin{array}{l} X_i^t + {r_1}{\rm{sin}}({r_2})\left| {{r_3}P_i^t-X_i^t} \right|, \;\;\;{r_4} < 0.5;\\ X_i^t + {r_1}{\rm{cos}}({r_2}){\rm{ }}\left| {{r_3}P_i^t-X_i^t} \right|, \;\;\;\;{r_4} \ge 0.5。\end{array} \right. $ | (9) |
式中:Xit为当前解的第i维第t次迭代空间位置;r1, r2, r3均为随机数;Pit为第i维第t次迭代目标点的空间位置。参数r1决定了下一空间位置区域(或移动方向),该区域可以是候选解和目标解之间的任一空间或之外的空间;参数r2定义了在移动方向上移动的步长;参数r3提供了随机选择权,即随机强调(r3>1)或淡化(r3 < 1)对所定义距离的影响;参数r4表示如何选择在式(9)中的正弦和余弦分量之间的切换。
一种优秀的算法应能平衡勘探和开采能力,以遍历搜索空间内所有区域,并最终收敛到全局最优[14]。为了平衡SCA中正余弦函数在搜索范围内的勘探和开采能力,应用式(10)来调整参数r1的自适应变化策略:
| $ {r_1} = b-t\frac{b}{T}, $ | (10) |
式中:t为当前迭代次数;T为最大迭代次数;b为常数。
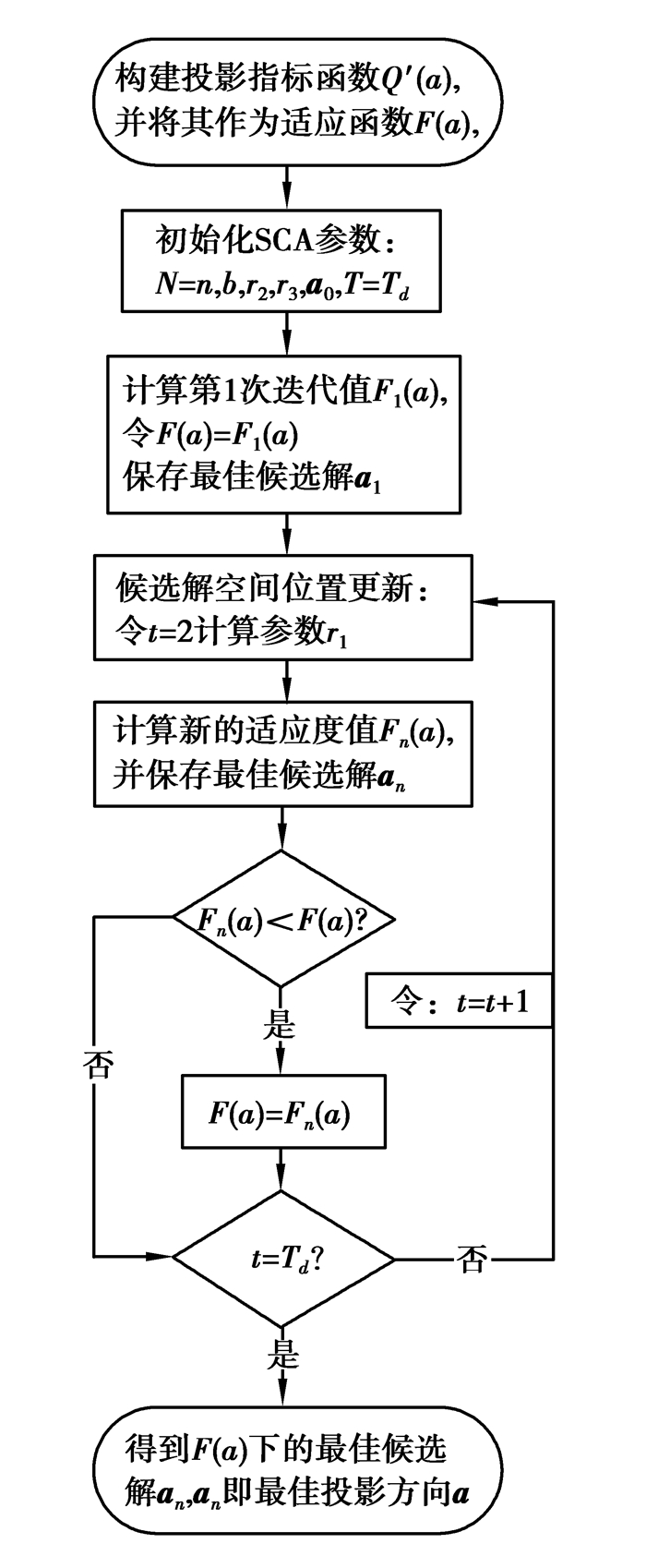
2.3 基于SCA的PP模型基于SCA的PP模型建立过程如图 2,整个过程可用Matlab M语言实现。
|
图 2 基于SCA的PP模型流程图 Figure 2 PP model procedure based on SCA |
1) 确定投影指标函数。因SCA是求解极小值,所以将式(4)取倒数作为投影指标函适即适应度函数:
| $ \left\{ \begin{array}{l} {\rm{min}}:Q'\left( a \right) = 1/({S_z}{D_z}), \\ {\rm{s}}{\rm{.t:}}\sum\limits_{j = 1}^n {a_j^2 = 1, {a_j} \in } \left[{0, 1} \right]。\end{array} \right. $ | (11) |
2) 初始化算法参数。设置群体数目N、常数b、参数r2、r3,算法搜索空间,在解空间内随机初始化候选解空间位置a0并设置算法终止条件即最大迭代次数T。
3) 计算并保存当前群体中的第一次迭代适应度值F1(a)和最佳候选解a1。
4) 令t=2, 利用式(10)计算参数r1,利用式(9)更新候选解位置。
5) 计算新候选解的适应度值Fn(a),并与前次迭代最佳候选解的适应度值进行比较。若当前候选解的适应度值小于前次候选解的适应度值,则保存当前候选解an为最佳候选解;否则保存前次候选解为最佳候选解。
6) 判断迭代次数是否满足终止条件,若满足,则转到步骤7,否则令t=t+1,重复执行步骤5,6。
7) 输出最优候选解的适应度值所处的空间位置,最优候选解所处的空间位置即最佳投影方向a。
图 2中符号“=”为计算机编程语言的赋值符号,F(a)=Fn(a)表示将内存中变量Fn(a)值赋给变量F(a),变量F(a)用来存储每次比较过后小的适应度值。
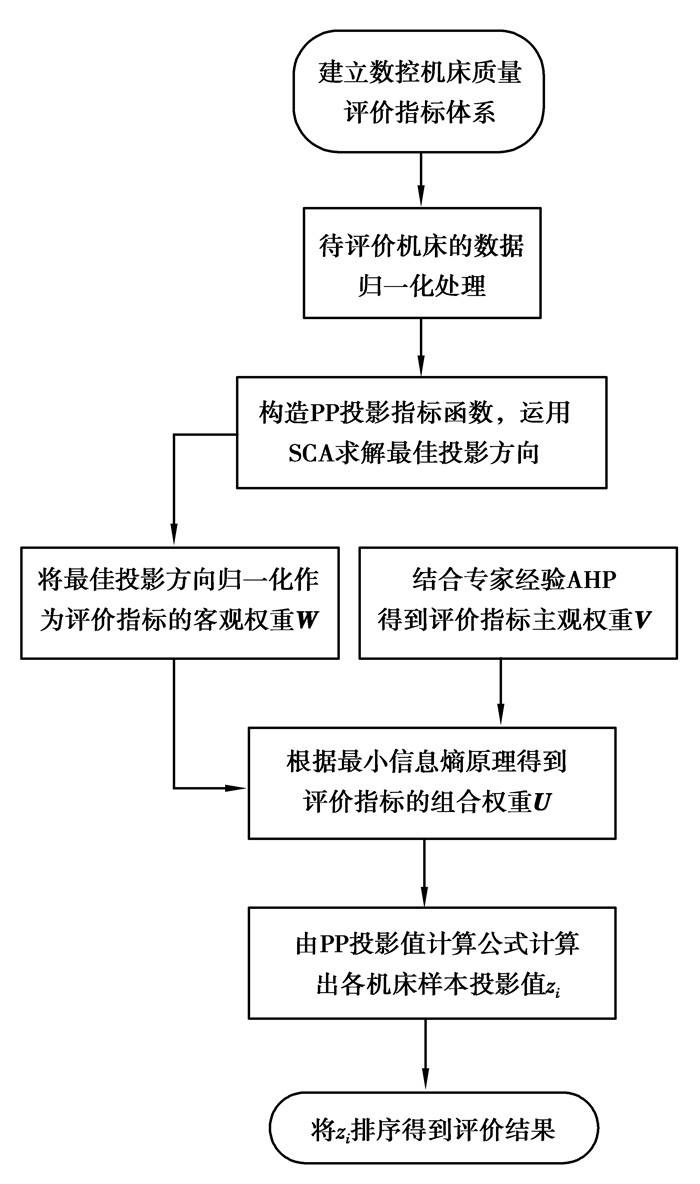
3 数控机床质量评价步骤数控机床质量评价概括步骤如图 3所示,详细步骤如下。
|
图 3 数控机床质量评价流程图 Figure 3 CNC machine tool quality evaluation procedure |
1) 建立数控机床质量评价指标集,如图 1所示。
2) 收集数控机床的样本数据,并根据评价指标的具体属性(效益型或成本型)选择式(1)或者式(2)对数据作归一化处理。
3) 构建投影指标函数。因采用SCA求解投影指标函数的最佳投影方向,所以按照式(11)构建投影指标函数。
4) 用SCA计算最佳投影方向a,并将其归一化作为评价指标客观权重a′,a′ = [a'1, a'2, …, a'n],n为评价指标数,令W = [w1, w2, …, wn],wj=a′ j,W为评价指标的客观权重向量。
5) 由步骤4所得W仅仅是评价指标的客观权重,该权重基于数据本身,反映了数据的信息量和特点。为了使评价更具全面性和科学性,笔者结合专家经验,由AHP得出主观评价权重向量V = [v1, v2, …vn],鉴于AHP在机械领域已经得到广泛使用,限于篇幅,不再赘述其具体实施过程。
6) 评价指标组合赋权。由各指标的客观权重W和主观权重V求解各评价指标的组合权重U,U =[u1, u2, …un]。为了使uj在空间中的分布与wj,vj都尽量接近,根据最小信息熵原理[15-17]:
| $ \left\{ \begin{array}{l} {\rm{min}}F = \sum\limits_{j = 1}^n {{u_j}\left[{\ln \;{u_j}-\ln \;{w_j}} \right] + \sum\limits_{j = 1}^n {{u_j}\left[{\ln \;{u_j}-\ln \;{v_j}} \right]}, } \\ {\rm{s}}{\rm{.t}}\sum\limits_{j = 1}^n {{u_j}} = 1({u_j} > 0, j = 1, 2, \ldots, n)。\end{array} \right. $ | (12) |
由拉格朗日乘子法求解式(12)优化问题[18-19],可得:
| $ {u_j} = \frac{{\sqrt {{w_j}{v_j}} }}{{\sum\limits_{j = 1}^n {{w_j}{v_j}} }}。$ | (13) |
7) 根据投影值的计算公式(3),考虑由AHP所得到的客观权重对评价结果影响,将式(3)调整为:
| $ z{'_{i}} = \sum\limits_{j = 1}^n {{u_j}} x * \left( {i, j} \right), $ | (14) |
z'i即为数控机床质量综合评价值,将综合评价值排序可得到评价结果。
4 实例分析为了验证该方法的可行性,笔者引用文献[12]的样本数据,见表 1。
| 表 1 数控机床质量特性指标[12] Table 1 CNC machine tool quality characteristic index |
表 1中的价格、定位精度、重复定位精度、最小分辨率、平均故障维修时间tMTTR、故障率、换刀时间是成本型指标,用式(2)归一化处理;平均故障间隔时间tMTBF、使用可用度、主轴最大转速、进给速度是效益型指标,用式(1)归一化处理,得到最后归一化的矩阵x *为
| $ {\mathit{\boldsymbol{x}}^*} = \left[\begin{array}{l} 0.333\;3\;\;\;1.000\;0\;\;\;0.333\;3\;\;\;0.250\;0\;\;\;0.000\;0\;\;\;1.000\;0\;\;\;1.000\;0\;\;\;0.500\;0\;\;\;0.666\;7\;\;\;0.666\;7\;\;\;0.200\;0\;\;\;\\ 0.824\;6\;\;\;0.000\;0\;\;\;0.666\;7\;\;\;1.000\;0\;\;\;1.000\;0\;\;\;0.562\;5\;\;\;0.642\;6\;\;\;0.875\;0\;\;\;0.333\;3\;\;\;0.000\;0\;\;\;0.600\;0\;\;\;\\ 0.000\;0\;\;\;0.666\;7\;\;\;1.000\;0\;\;\;0.750\;0\;\;\;0.333\;3\;\;\;0.250\;0\;\;\;0.000\;0\;\;\;0.000\;0\;\;\;1.000\;0\;\;\;1.000\;0\;\;\;1.000\;0\;\;\;\\ 1.000\;0\;\;\;0.000\;0\;\;\;0.000\;0\;\;\;0.250\;0\;\;\;1.000\;0\;\;\;0.437\;5\;\;\;0.401\;4\;\;\;0.125\;0\;\;\;0.000\;0\;\;\;0.333\;3\;\;\;0.400\;0\;\;\;\\ 0.929\;8\;\;\;0.333\;3\;\;\;0.333\;3\;\;\;0.000\;0\;\;\;0.666\;7\;\;\;0.000\;0\;\;\;0.552\;8\;\;\;1.000\;0\;\;\;0.666\;7\;\;\;0.000\;0\;\;\;0.000\;0\;\;\;\;\;\; \end{array} \right]。$ |
将2.3中步骤1~7用Matlab M语言编程实现,设置群体数目N=30,最大迭代数T=1 000,常数b=2,r2=2πrand(),r3=2rand(),SCA搜索空间设置为[0,1]。得到数控机床评价指标最佳投影方向:
| $ \mathit{\boldsymbol{a = }}\left[{0.053\;7, 0.302\;9, 0.419\;7, \;0.489\;5, 0.098\;1, \\0.228\;9, 0.118\;6, \;0.125\;9, 0.251\;7, 0.412\;9, 0.377\;1} \right]。$ |
将其归一化得到评价指标的客观权重:
| $ \mathit{\boldsymbol{W = }}\left[{0.018\;2, 0.102\;7, 0.142\;3, 0.166\;0, 0.033\;3,\\ 0.077\;6, 0.064\;0, 0.042\;7, 0.085\;3, 0.140\;0, 0.127\;9} \right]。$ |
结合专家经验,运用AHP确定评价指标的判断矩阵为
| $ \mathit{\boldsymbol{A = }}\left[{\begin{array}{*{20}{c}} 1&2&4&1&6&5&9&2&7&3&5\\ {1/2}&1&2&{1/2}&3&2&6&1&5&4&4\\ {1/4}&{1/2}&1&{1/4}&2&1&3&1&2&3&2\\ 1&2&4&1&2&3&7&1&6&4&5\\ {1/6}&{1/3}&{1/2}&{1/2}&1&1&2&{1/2}&4&5&6\\ {1/5}&{1/2}&1&{1/3}&1&1&2&{1/2}&3&2&2\\ {1/9}&{1/6}&{1/3}&{1/7}&{1/2}&{1/2}&1&{1/4}&1&{1/2}&{1/2}\\ {1/2}&1&1&1&2&2&4&1&3&3&2\\ {1/7}&{1/5}&{1/2}&{1/6}&{1/4}&{1/3}&1&{1/3}&1&1&{1/2}\\ {1/3}&{1/4}&{1/3}&{1/4}&{1/5}&{1/2}&2&{1/3}&1&1&1\\ {1/5}&{1/4}&{1/2}&{1/5}&{1/6}&{1/2}&2&{1/2}&2&1&1 \end{array}} \right]。$ |
根据AHP的一致性判断条件CR < 0.1,对判断矩阵进行一致性检验:矩阵特征值λ=11.623, CR=0.041 0 < 0.1,由此可知判断矩阵具有一致性。经计算,AHP的评价权重向量为
| $ \mathit{\boldsymbol{V = }}\left[{0.229\;8, 0.136\;2, 0.075\;7, 0.184\;4, 0.073\;7, 0.064\;8, \\0.025\;4, 0.110\;5, 0.027\;5, 0.035\;1, 0.036\;9} \right]。$ |
由式(13)计算得到评价指标的组合权重:
| $ \mathit{\boldsymbol{U = }}\left[{0.073\;6, 0.134\;7, 0.118\;2, 0.199\;2, 0.056\;4, 0.080\;7, \\0.045\;9, 0.078\;2, 0.055\;2, 0.079\;8, 0.078\;2} \right]。$ |
根据式(14)计算得到各机床指标的投影值:
| $ \mathit{\boldsymbol{Z = }}\left[{0.519\;72, 0.603\;68, 0.609\;47, 0.301\;21, 0.330\;66} \right]。$ |
由投影值得到数控机床质量综合评价结果:Z3>Z2>Z1>Z5>Z4,由排序的结果可知机床3综合质量最好,机床2的综合质量次之,与参考文献[10]的研究结果基本一致。由此可见,基于PP模型的数控机床质量综合评价方法切实可行。该方法一方面结合了主客观评价的优点,使评价更全面、更科学;另一方面该方法中的SCA稳健性较好,并且通过PP原理将多维评价指标投影到一维投影值,简化了评价过程。
5 结语数控机床多维性指标下的质量评价是一个复杂问题。笔者引入正弦余弦算法求解投影寻踪模型的最佳投影方向,将最佳投影方向归一化后作为机床质量评价指标的客观权重。该方法基于数据驱动,根据评价指标样本集的分布特征,客观地确定不同样本之间评价指标的变化信息。
考虑数控机床质量特性指标的实际重要度,结合专家经验,运用层次分析法得出评价指标的客观权重。为了充分利用主客观权重的优点,根据最小信息熵原理和拉格朗日乘子法得到组合权重,在组合权重的基础上由投影寻踪原理计算出样本投影值。按投影值排序,得到数控机床质量综合评价结果。笔者通过实例验证了该方法切实可行,评价结果符合客观实际。该评价方法易用计算机编程语言实现,封装成程序,为多维性指标下的数控机床质量评价提供了一种新方法,同时也为企业和客户决策提供较为可靠的科学依据。
| [1] |
李如琦, 苏浩益.
基于可拓云理论的电能质量综合评估模型[J]. 电力系统自动化, 2012, 36(1): 66–70.
LI Ruqi, SU Haoyi. A synthetic power quality evaluation model based on extension cloud theory[J]. Automation of Electric Power Systems, 2012, 36(1): 66–70. (in Chinese) |
| [2] |
刘志峰, 王淑旺, 万举勇, 等.
基于模糊物元的绿色产品评价方法[J]. 中国机械工程, 2007, 18(2): 166–170.
LIU Zhifeng, WANG Shuwang, WAN Juyong, et al. Green product assessment method based on fuzzy-matter element[J]. China Mechanical Engineering, 2007, 18(2): 166–170. (in Chinese) |
| [3] |
刘玉梅, 赵聪聪, 熊明烨, 等.
基于物元模型的高速轨道车辆传动系可靠性评价[J]. 吉林大学学报(工学版), 2015, 45(4): 1064–1068.
LIU Yumei, ZHAO Congcong, XIONG Mingye, et al. Reliability assessment of high-speed railway train based on matter-element model[J]. Journal of Jilin University (Engineering Edition), 2015, 45(4): 1064–1068. (in Chinese) |
| [4] |
李菲, 沈虹.
面向再制造的产品质量特性评价方法[J]. 现代制造工程, 2008(11): 99–102.
LI Fei, SHEN Hong. Study of evaluation method of product quality characteristics for remanufacturing[J]. Modern Manufacturing Engineering, 2008(11): 99–102. DOI:10.3969/j.issn.1671-3133.2008.11.029 (in Chinese) |
| [5] | Pal R, Mitra J, Pal M N. Evaluation of relative performance of product designs:a fuzzy DEA approach to quality function deployment[J]. Opsearch, 2007, 44(4): 322–336. DOI:10.1007/BF03398797 |
| [6] | Azadeh A, Ghaderi S F, Ahmadabad M F. Multi criteria quality assessment of products by integrated DEA-PCA approach[J]. International Journal of Reliability, Quality and Safety Engineering, 2007, 14(3): 201–218. DOI:10.1142/S0218539307002593 |
| [7] |
付忠广, 齐敏芳.
基于最大熵投影寻踪耦合的燃煤机组节能减排评价方法研究[J]. 中国电机工程学报, 2014, 34(26): 4476–4482.
FU Zhongguang, QI Minfang. Study on the evaluation method of energy-saving and emission reduction of coal-fired units based on projection pursuit method coupled with maximum entropy[J]. Proceeding of the CSEE, 2014, 34(26): 4476–4482. (in Chinese) |
| [8] |
付忠广, 景源, 齐敏芳, 等.
基于投影寻踪原理的机组可靠性等级评价[J]. 动力工程学报, 2012, 32(10): 820–824.
FU Zhongguang, JING Yuan, QI Minfang, et al. Reliability grade evaluation of power plant based on projection pursuit[J]. Journal of Chinese Society of Power Engineering, 2012, 32(10): 820–824. DOI:10.3969/j.issn.1674-7607.2012.10.014 (in Chinese) |
| [9] | Berro A, Marie-sainte S L, Ruiz-gazen A. Genetic algorithms and particle swarm optimization for exploratory projection pursuit[J]. Annals of Mathematics and Artificial Intelligence, 2010, 60(1): 153–178. |
| [10] |
张根保, 庞继红, 陈国华, 等.
数控装备质量的模糊物元综合评价方法[J]. 重庆大学学报, 2011, 34(1): 36–41.
ZHANG Genbao, PANG Jihong, CHEN Guohua, et al. A comprehensive evaluation method of fuzzy matter element for CNC equipment quality[J]. Journal of Chongqing University, 2011, 34(1): 36–41. (in Chinese) |
| [11] |
付强, 赵小勇. 投影寻踪模型原理及其应用[M]. 北京: 科学出版社, 2006.
FU Qiang, ZHAO Xiaoyong. Principle and application of projection pursuit model[M]. Beijing: Science Press, 2006. (in Chinese) |
| [12] | Mirjalili S. SCA:A Sine Cosine Algorithm for solving optimization problems[J]. Knowledge-based Systems, 2016, 96: 120–133. DOI:10.1016/j.knosys.2015.12.022 |
| [13] |
崔东文.
正弦余弦算法-投影寻踪水污染物总量分配模型[J]. 水资源保护, 2016, 32(6): 75–81.
CUI Dongwen. Sine cosine algorithm-projection pursuit model for water pollutant load allocation[J]. Water Resources Protection, 2016, 32(6): 75–81. (in Chinese) |
| [14] | Mirjalili S, Jangir P, Saremi S. Multi-objective ant lion optimizer:a multi-objective optimization algorithm for solving engineering problems[J]. Applied Intelligence, 2017, 46(1): 79–95. DOI:10.1007/s10489-016-0825-8 |
| [15] |
马胜蓝, 叶东毅.
信息熵最小约简问题的若干随机优化算法[J]. 模式识别与人工智能, 2012, 25(1): 96–104.
MA Shenglan, YE dongyi. Research on computing minimum entropy based attribute reduction via stochastic optimization algorithm[J]. PTA & AT, 2012, 25(1): 96–104. (in Chinese) |
| [16] | Sadovsky M G. The method to compare nucleotide sequences based on the minimum entropy principle[J]. Bulletin of Mathematical Biology, 2003, 65(2): 309–322. DOI:10.1016/S0092-8240(02)00107-6 |
| [17] | Zhang B, Hamid M O A, Liu W J. Numerical and experimental study of field synergy analysis in water jet impingement based on minimum entropy generation method[J]. Applied Thermal Engineering, 2016, 99: 944–958. DOI:10.1016/j.applthermaleng.2016.01.157 |
| [18] | Feldman Y, Gulberg Y. An extension of the immersed boundary method based on the distributed Lagrange multiplier approach[J]. Journal of Computational Physics, 2016, 32: 248–266. |
| [19] | Mokhtar M A, Darpe A K, Gupta K. Investigations on bending-torsional vibrations of rotor during rotor-stator rub using Lagrange multiplier method[J]. Journal of Sound and Vibration, 2017, 401: 94–113. DOI:10.1016/j.jsv.2017.03.026 |
 2018, Vol. 41
2018, Vol. 41


