变桨轴承作为风力发电机组变桨系统关键零部件,其性能的好坏对风力发电机组的安全运行具有很大的影响,因此要求变桨轴承具有高可靠性[1]。而滚珠-滚道的载荷分布决定了滚珠、滚道的变形,直接影响变桨轴承的寿命及可靠性,因此,为确保风力发电机组的安全运行,对变桨轴承的载荷影响因素的研究具有重要意义[2-3]。
目前,国内外学者对四点接触球轴承做了大量研究。Glodež等[4]利用有限元法建立变桨轴承的仿真模型,利用该模型计算了滚珠-滚道的接触载荷分布,并与理论公式比较,验证了模型的可靠性。Kania等[5]基于建立的静力学模型得到轴承的载荷分布。王燕霜等[6]基于赫兹接触等基本理论,建立变桨轴承载荷分布的静力学分析模型,并分析了变桨轴承结构参数对轴承滚珠-滚道接触载荷分布的影响;陈国桢等[7]基于静力学理论,建立变桨轴承考虑柔性支撑的静力学分析模型,并基于此模型分析了变桨轴承的载荷分布。王永全等[8]利用等效压力模拟螺栓连接建立变桨轴承有限元简化模型,与经验公式对比验证模型的可靠性,并分析了螺栓预紧力对变桨轴承载荷分布及疲劳寿命的影响。
以上大部分文献都没有考虑螺栓预紧力、安装表面平面度以及变桨过程中的变桨同步度对轴承载荷分布的影响。但在实际工作中,螺栓预紧力、安装表面平面度及变桨同步度对轴承受力状态的影响不容忽略。笔者在前人对大型双排四点接触球轴承研究基础上,提出了一种新型模型简化方法,利用赫兹接触理论及有限元分析方法建立合理的有限元模型,并对螺栓预紧力、安装表面平面度及变桨同步度对轴承载荷分布的影响进行了详细分析。
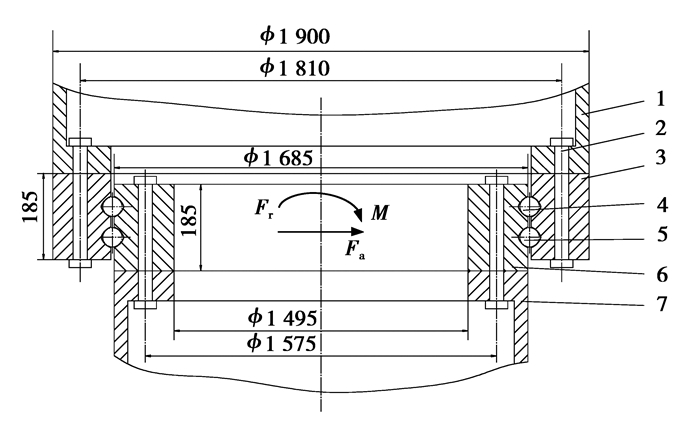
1 变桨轴承有限元分析模型本文的研究对象为某型风机发电机用变桨轴承,该变桨轴承属于大型双排四点接触球轴承。轴承的安装示意图及主要尺寸如图 1所示,其中轴承的节圆直径为1 685 mm,滚珠直径为50.5 mm,轴承上、下排的中心距为70 mm。
|
图 1 变桨轴承几何安装尺寸 Figure 1 The installation geometric dimension of blade bearing 1—叶片;2—连接螺栓;3—外圈;4—滚道上;5—滚道下;6—内圈;7—轮毂 |
该变桨轴承有限元分析模型主要包括轮毂、变桨轴承以及叶根三大部分,建立有限元分析模型需要对几何模型中存在的圆角等一些不利于划分网格的几何特征进行删除,既能简化模型又能提高网格划分的质量。
变桨轴承滚珠直径为50.5 mm,且滚珠与螺栓数量分别为168、74个,如果对轴承进行实体建模分析,就需要建立相同数量的接触对,这就需要很高的计算能力以及计算时间。因此,对变桨轴承的滚珠-滚道与螺栓连接进行简化模拟很有必要。
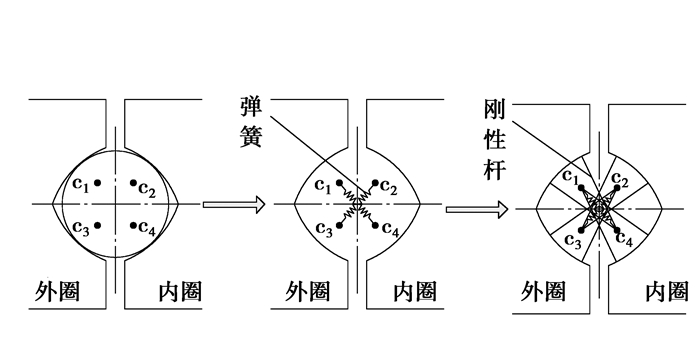
1.1 滚珠与滚道接触模拟笔者采用非线性弹簧单元COMBIN39及刚性杆单元MPC184简化模拟滚珠-滚道接触,并保证弹簧单元的刚度与滚珠-滚道接触刚度一致,如图 2所示。
|
图 2 轴承滚珠-滚道模拟 Figure 2 The contact simplification of raceway and ball |
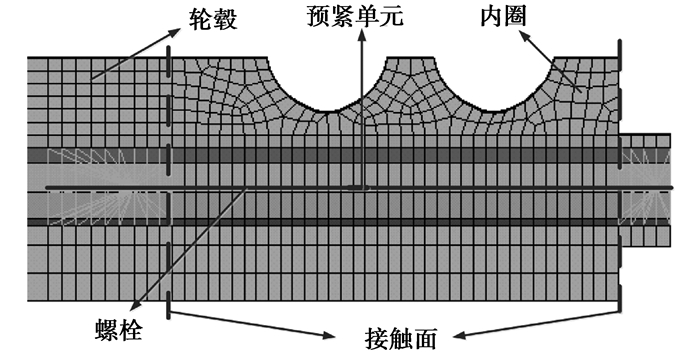
根据螺栓工程计算标准VDI2230准则,采用等效梁[10-11]对螺栓连接进行简化,即利用杆、梁单元简化螺栓连接,预紧力使用预紧力单元Prets179。具体简化模拟方式如图 3所示。
|
图 3 螺栓有限元简化模型 Figure 3 The FE simplified model of bolt |
采用GL规范叶根坐标系,在叶根部位建立加载点,通过载荷伞将载荷传递到轴承外圈,再通过滚珠传递至内圈,最后由内圈通过螺栓传递给轮毂。施加的极限载荷如表 1所示。
| 表 1 Mxy_max工况载荷 Table 1 The max Mxy load case |
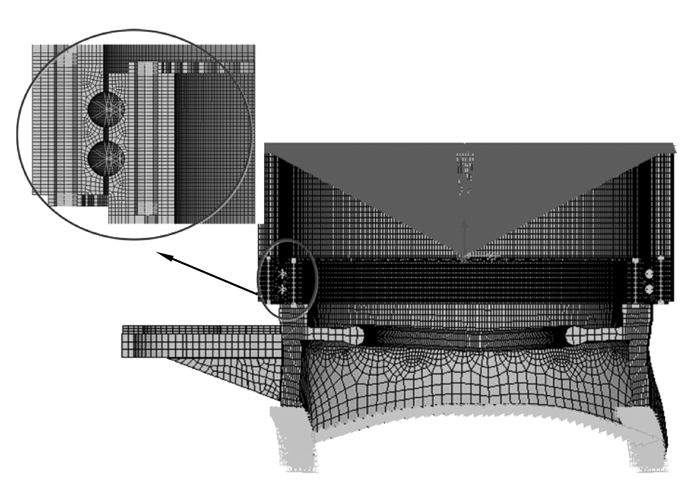
根据模型零部件之间的相互作用关系,设置模型的约束为轮毂3个方向的位移全约束,建立刚性区主节点绕Z轴的转动自由度约束,如图 4所示。不同部件之间的接触单元设置如表 2所示。
|
图 4 变桨轴承有限元模型 Figure 4 FE model for pitch bearing |
| 表 2 模型部件接触单元设置 Table 2 The contact element of modeling component |
对模型设置材料属性,模型中各部件的材料如表 3所示。
| 表 3 模型材料参数 Table 3 Material parameters of all components |
建立的模型如图 4所示。由于轮毂结构是对称性结构,且为减少模型计算时间,取轮毂的1/3作为研究对象。为保证计算精度,笔者同时使用力收敛准则及位移收敛准则,并分别设置收敛容差为0.5%, 0.1%。
2 变桨轴承有限元模型验证分别采用理论模型及经验公式验证建立的有限元模型的计算精度,为下一步研究螺栓预紧力等因素对轴承载荷分布的影响提供正确的模型基础。
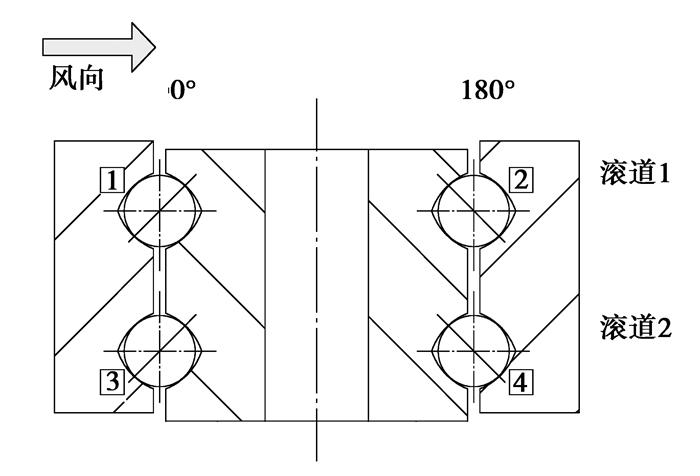
在进行有限元计算时,为使结果更直观取迎风面为0°方位角(逆时针方向递增至360°),接触对1,2,3,4如图 5所示。
|
图 5 轴承滚珠方位角设置 Figure 5 The position angle and setting of bearing |
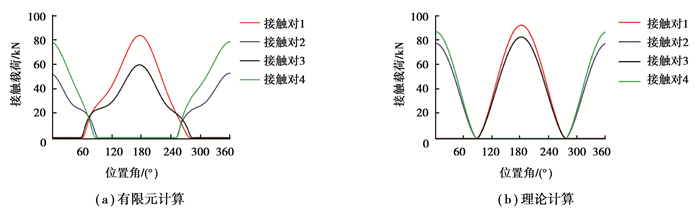
在结构参数、施加的外载等外部条件一致的情况下,分别采用理论模型[12]及建立的有限元简化模型计算轴承在极限载荷下的载荷分布,如图 6所示。
|
图 6 不同模型下接触载荷分布 Figure 6 The contact load distribution under different model |
由图 6可知,有限元模型计算的轴承载荷分布与理论计算的载荷分布趋势是相同的。但理论计算将模型理想化,没有考虑轴承套圈和支撑结构的变形。
在轴承计算中,为了获得最大接触载荷,一般的经验公式[13]如下:
承受纯轴向力
| $ {Q_{{\rm{max}}}} = {F_{\rm{a}}}/(Z{\rm{sin}}\;\alpha ), $ | (1) |
承受纯倾覆力矩
| $ {Q_{{\rm{max}}}} = 4.37M/({d_{\rm{m}}}Z{\rm{sin}}\;\alpha ), $ | (2) |
承受纯径向力
| $ {Q_{{\rm{max}}}} = 2.37{F_{\rm{r}}}/(Z{\rm{sin}}\;\alpha ), $ | (3) |
式中:Fa为轴向载荷;Fr为径向载荷;M为力矩;Z为滚珠数;α为接触角;dm为轴承节圆直径。
通过对建立的轴承有限元模型及经验公式分别施加极限载荷下的纯轴向力、径向力和倾覆力矩进行计算验证。有限元算法与经验公式计算结果如表 4所示。
| 表 4 不同算法下轴承最大接触载荷 Table 4 the max contact load of bearing under different arithmetic |
由表 4可知,有限元模型最大接触载荷计算结果对比经验公式计算结果,最大误差为3.4%。证明所提出的有限元简化模型是可行的。但相比有限元分析模型能计算在轴向载荷、径向载荷、倾覆力矩联合载荷作用下轴承接触载荷,理论公式只能计算轴承承受纯轴向载荷、径向载荷或倾覆力矩下的接触载荷。
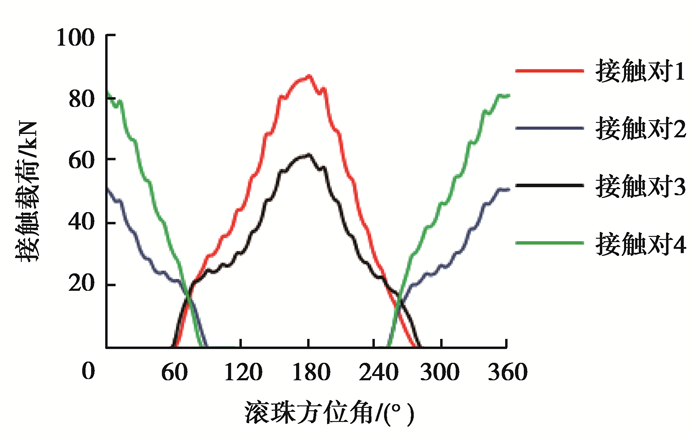
3 载荷分布研究 3.1 螺栓预紧力对载荷分布的影响为充分研究螺栓预紧力对变桨轴承载荷分布的影响,通过对建立的有限元简化模型分别施加150,250,450,500,700 kN的螺栓预紧力,假设安装平面为理论纯平,无平面度误差得到其载荷分布曲线如图 7所示。
|
图 7 螺栓预紧力为500kN时载荷分布 Figure 7 The load distribution for 500 kN bolt pretension |
对比图 7有螺栓计算结果与图 6无螺栓计算结果可知,在螺栓预紧力的作用下变桨轴承的最大接触载荷增大,且载荷分布曲线有小幅的上下波动,由于是在螺栓连接位置处,由于螺栓预紧力的作用导致该处附近的套圈滚道有微量变形。
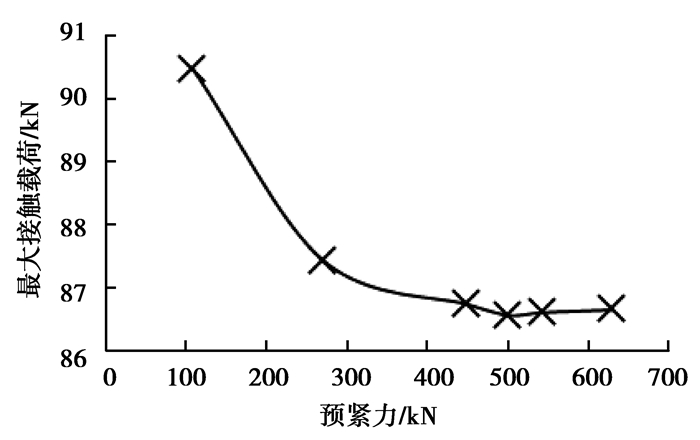
由图 8可知,在不同预紧力作用下,滚珠-滚道的最大接触载荷不同,且在500 kN预紧力作用下,滚珠-滚道的最大接触载荷最小。当作用的预紧力小于500 kN时,随着螺栓预紧力的增大,轴承最大接触载荷减小,当作用的预紧力低于300 kN时,最大接触载荷随预紧力的变化,变化幅度增大。这是由于螺栓预紧力过小时,在弯矩M作用下,轴承容易发生偏斜,变形加大,导致接触载荷增大。
|
图 8 螺栓预紧力下滚珠-滚道最大接触载荷 Figure 8 The max contact load under different bolt pretension |
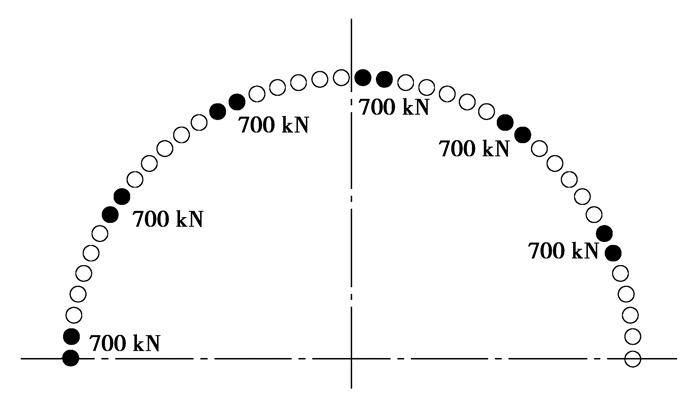
为充分研究螺栓预紧力作用不均对轴承载荷分布的影响,选择如图 9所示螺栓预紧力分布(“●”处螺栓预紧力为700 kN,“○”处螺栓预紧力为150 kN)。对应轴承载荷分布如图 10所示。
|
图 9 螺栓预紧力分布 Figure 9 The bolt pretension distribution |
|
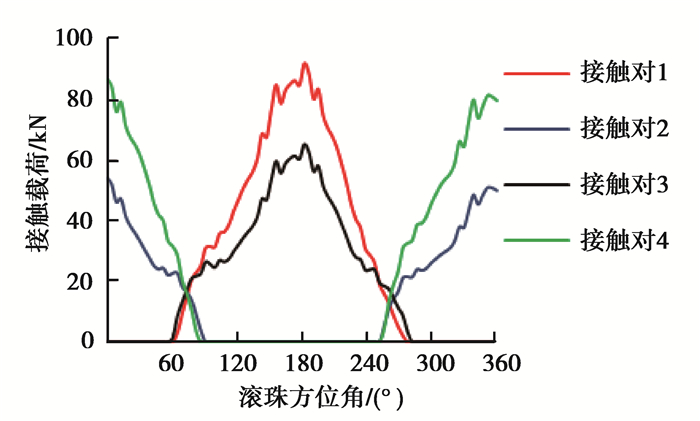
图 10 非均布预紧力时接触载荷分布 Figure 10 The contact load for uneven bolt pretension |
从图 10可知,当螺栓预紧力作用不均时对滚珠-滚道的载荷分布有明显的影响,在螺栓预紧力变化的位置接触载荷有明显波动,加大了接触载荷分布不均,从而影响轴承疲劳寿命。
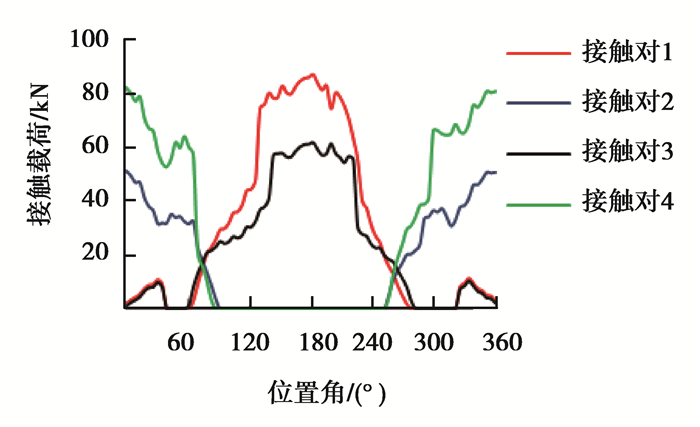
3.3 安装平面度对载荷分布的影响对螺栓施加500 kN的预紧力,叶根端面平面度误差为0.2。轴承载荷分布如图 11所示。
|
图 11 平面度误差为0.2时接触载荷分布 Figure 11 The contact load distribution under 0.2 mounting surface flatness |
对比图 11端面平面度误差为0.2计算结果与图 7安装表面纯平计算结果可知,当轴承表面存在平面度误差、外部载荷施加到轴承上时,变桨轴承的接触载荷分布发生了极不规则的突变。这是由于平面度误差使轴承支撑表面发生不规则变形,导致轴承接触载荷分布发生不规则突变。
3.4 变桨同步度对载荷分布的影响在风机实际运行过程中,由于机构运动误差或者机构变形等因素,导致风机3个叶片实际变桨位置不一致。3个浆距角的不同会造成风机受力不均衡,影响风机的安全运行。
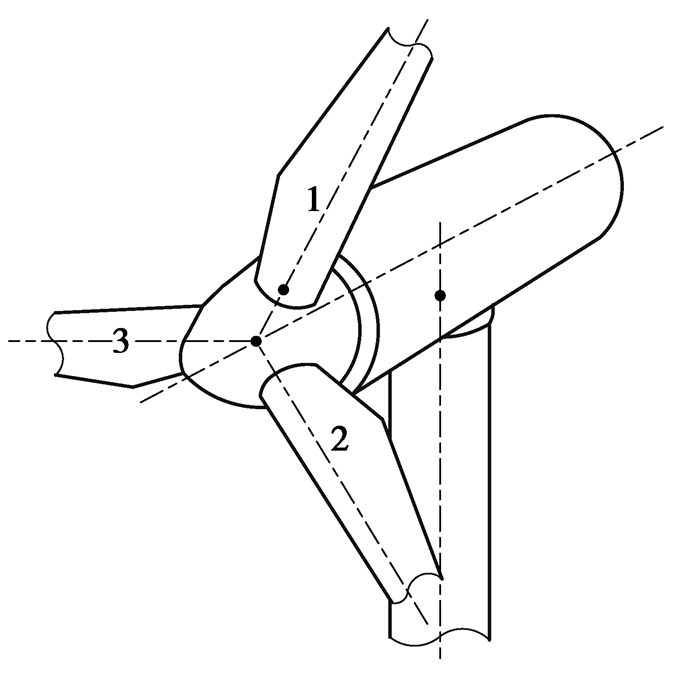
为充分研究变桨不一致对载荷分布的影响,笔者通过simpack建立了整机联合仿真模型[14]。对叶片与轮毂之间的铰接设定不同的值以对不同叶片之间的变桨不一致进行模拟,即对叶片1和轮毂的铰接设定不同值来模拟叶片1在运行过程中相对于其他两叶片的变桨误差,2,3号叶片的浆距角与变桨控制模型的指令指定的浆距角一样。叶片编号设置如图 12所示。
|
图 12 叶片模型编号 Figure 12 The rotor blade numbers |
分别对3个叶片同步度误差为-2°、0°和+2°时进行分析,并分别提取相对于其他两叶片变桨不同同步度下叶片1叶根处所承受的最大载荷,如表 5所示。
| 表 5 不同同步度下叶根处所受最大载荷 Table 5 The max load on the blade under different pitch angles |
将提取的载荷施加到建立的有限元模型中,得到轴承的载荷分布如图 13所示。
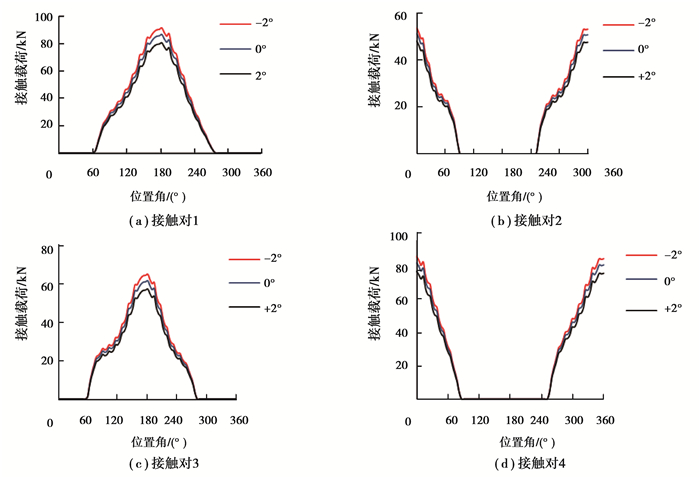
|
图 13 不同变桨同步度下变桨轴承接触载荷分布 Figure 13 The contact load distribution under different pitch angles |
由图 13及表 5可知,当同步度误差为-2°时,变桨轴承受载荷及滚珠-滚道接触载荷增大。这是由于当1号叶片相较于另外两叶片的变桨同步度误差为负时,1号叶片的浆距角小于另外两叶片的浆距角,导致1号叶片受到风载荷大,进而使变桨轴承滚珠-滚道的接触载荷增大。所以在风机运行过程中,由于叶片变桨不一致会导致变桨轴承滚珠-滚道的最大接触载荷增大,另外当受到的风载过大时,该变桨轴承有被压溃失效的危险,影响风机的可靠运行。
4 结论1) 建立了双排四点球轴承非线性滚珠滚道接触模型,并与理论模型及经验公式计算结果对比,证明了简化模型的有效性。
2) 在均布螺栓预紧力下,轴承最大接触载荷随着螺栓预紧力增加,轴承最大接触载荷先呈减小趋势,然后小幅增加。
3) 在非均布螺栓预紧力下,轴承接触载荷分布波动增强,预紧力变化的位置接触载荷发生突变。
4) 当安装端面存在平面误差时,轴承接触载荷分布出现不规则突变。因此,在变桨轴承制造加工及安装过程中,要严格检测轴承的平面度。
5) 当变桨同步度为负时,轴承受载增大,其载荷分布也相应增大。在风机运行中,尽量避免变桨不一致的问题。
| [1] |
俞黎萍, 石亦平, 刘瑞峰.
风电机组主轴承选型与设计分析[J]. 重庆大学学报, 2015, 38(2): 80–86.
YU Liping, SHI Yiping, LIU Ruifeng. Arrangement and design of main bearing for wind turbine[J]. Journal of Chongqing University, 2015, 38(2): 80–86. DOI:10.11835/j.issn.1000-582X.2015.02.012 (in Chinese) |
| [2] |
张建. 基于柔性支撑的转盘轴承性能及结构参数研究[D]. 大连理工大学, 2015. ZHANG Jian. Research on performances and structural parameters of slewing bearing with flexible supporting Structures[D]. Dalian University of Technology, 2015. (in Chinese) |
| [3] | Špiewak S. Methodology for calculating the complete static carrying capacity of twin slewing bearing[J]. Mechanism and Machine Theory, 2016, 101: 181–194. DOI:10.1016/j.mechmachtheory.2016.03.017 |
| [4] | Glodež S, Potoĉnik R, Flašker J. Computational model for calculation of static capacity and life time of large slewing bearing's raceway[J]. Mechanism and Machine Theory, 2012, 47(1): 16–30. |
| [5] | Kania L, Krynke M, Mazanek E. A catalogue capacity of slewing bearings[J]. Mechanism and Machine Theory, 2014, 58: 29–45. |
| [6] |
王燕霜, 袁倩倩.
负游隙对特大型双排四点接触球轴承载荷分布的影响[J]. 机械工程学报, 2012, 48(21): 110–115.
WANG Yanshuang, YUAN Qianqian. Research on static load-carrying capacity of large size double row four-point contact ball bearings[J]. Journal of Mechanical Design, 2012, 48(21): 110–115. (in Chinese) |
| [7] |
陈国桢, 徐绍仁, 杨友中, 等.
特大型负游隙四点接触球轴承接触应力分析[J]. 机械传动, 2009, 33(5): 83–85.
CHEN Guozhen, XU Shaoren, YANG Youzhong, et al. Analysis on contact stress of large size four-point contact ball bearing with negative axial internal clearance[J]. Journal of Mechanical Transmission, 2009, 33(5): 83–85. (in Chinese) |
| [8] |
王永全, 王华, 高学海, 等.
螺栓预紧力对转盘轴承载荷分布的影响[J]. 轴承, 2013(12): 13–16, 50.
WANG Yongquan, Wang Hua, GAO Xuehai, et al. Influence of bolt pretension on load distribution for slewing bearing[J]. Journal of bearing, 2013(12): 13–16, 50. DOI:10.3969/j.issn.1000-3762.2013.12.004 (in Chinese) |
| [9] | Guanci C, Jianmin W. Load performance of large-scale rolling bearings with supporting structure in wind turbines[J]. Journal of Tribology-Transaction of The ASME, 2012, 134(4): 041105. DOI:10.1115/1.4007349 |
| [10] |
龚国伟. 风电机组法兰螺栓连接建模与仿真技术研究[D]. 重庆大学, 2014. GONG Guowei. Modeling and simulation research about the flange bolts connection of wind turbine[D]. Chongqing University, 2014. (in Chinese) |
| [11] |
江术新. MW级风电机组变桨系统动力学及结构仿真分析[D]. 重庆大学, 2014. JIANG Shuxin. Structural and dynamics analysis on the pitch system of MW grade wind turbine[D]. Chongqing University, 2014. (in Chinese) |
| [12] |
Harris T A, korzalas M N. 罗继伟, 马伟, 译. 滚动轴承分析: 第一卷轴承技术的基本概念[M]. 北京: 机械工业出版社, 2009. LUO Jiwei, MA weiyi. Rolling Bearing Analysis, Essential concepts of bearing technology[M]. Beijing: Press of Mechanical industry, 2009. (in Chinese) |
| [13] |
邓四二, 贾群义, 王燕霜. 滚动轴承设计原理[M]. 北京: 中国标准出版社, 2009.
DENG Sier, JIA Qunyi, WANG Yanshuang. Rolling bearing design theory[M]. Beijing: China Standard Press, 2009. (in Chinese) |
| [14] |
杜静, 周云鹏, 李成武.
并网双馈风力发电机组整机建模与仿真[J]. 重庆大学学报, 2015, 38(2): 45–55.
DU Jing, ZHOU Yunpeng, LI Chengwu. Modeling and simulation of a grid connected wind turbine with doubly fed induction generator[J]. Journal of Chongqing University, 2015, 38(2): 45–55. DOI:10.11835/j.issn.1000-582X.2015.02.007 (in Chinese) |
 2018, Vol. 41
2018, Vol. 41

