b. 辽宁工程技术大学 煤炭资源安全开采与洁净利用工程研究中心, 辽宁 阜新 123000
b. Research Center of Coal Resources Safe Mining and Clean Utilization, Liaoning Technical University, Fuxin 123000, Liaoning, P. R. China
断层是地壳上普遍存在的一种地质构造[1-2]。由于复杂的地质力学作用,断层面往往不是规则的形态,而是不规则的空间曲面;受限于断层数据获取的艰难性和断层数据分布的稀疏性,基于传统轮廓线法重构断层面形态过于粗糙,不能很好还原断层的弯曲细节,严重影响三维地质模型的准确性和实用性[3]。因此,能否重构精准和平稳光滑的断层面对于三维地质模型的构建和应用意义重大。
断层面重构一直是三维地质建模研究的热点和难点,相关学者对于此问题进行研究。武强等[4-6]利用多个平面组合的方式来逼近复杂的断层面,以便能用数学语言描述断层的空间展布;朱良峰等[7-8]对不同来源和不同表现形式的断层数据进行标准化处理,为后续断层建模提供有利的数据支持;李兆亮等[9]针对复杂断层相交情况,提出了路径切割算法,提高了复杂断层网的建模效率;王润怀等[10]分析了地层与断层4种典型组合下边界虚拟钻孔的确定方法,使不连续地层形态得以控制。综合分析前人研究成果发现,各位学者根据不同的建模数据和建模方法对断层面空间形态进行描述,但并未考虑实际断层数据获取的艰难性和数量的稀疏性,在样本数据稀少的情况下对于复杂断层面形态的构建过于生硬粗糙甚至不合理。
笔者针对上述问题,通过分析不同断层建模数据特点,提出利用断层线为断层建模的基础数据,并基于Morphing方法建立相邻断层线之间的过渡曲线,以实现稀疏断层线之间的光滑渐变,并在此基础上对断层尖灭位置和断层切削关系进行研究,以实现对断层空间形态的全面构建。
1 断层建模数据分析与优选断层面建模数据主要通过野外地质调查、钻探工程、地球物理勘探、实际生产揭露等手段获得。根据不同的勘探手段得到的断层数据精度与类型不尽相同,大致可分为:断点数据、断层多边形、断层线数据等,下面对各种断层面建模数据进行分析与优选。
1.1 断点数据分析断点数据(fault point)通常由钻探工程和实际生产揭露获得,因数据量稀疏,不足以精确构建断层面模型。但当断层面为平面或近似为平面时,且已知其中一个断点信息和断层面的产状信息,可以通过数学语言来描述并快速构建断层面模型。
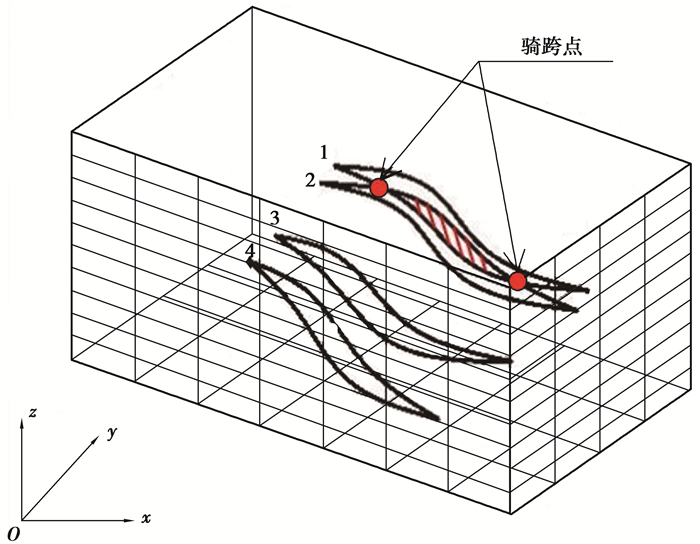
1.2 断层多边形分析断层多边形(fault polygon)是由三维地震或地质人员推断解释的数据,如图 1所示。通过提取各个煤层顶底板图中的断层多边形,经三角剖分,可以得到断层面模型。但此方法仅限于两相邻断层多边形未相交的情况,如图 1中3号、4号多边形的情况;当相邻断层多边形出现骑跨,即存在重叠区域,如图 1中1号、2号多边形的情况,此时不能正确实现三角剖分。
|
图 1 空间序列断层多边形 Figure 1 Spatial sequence fault polygon |
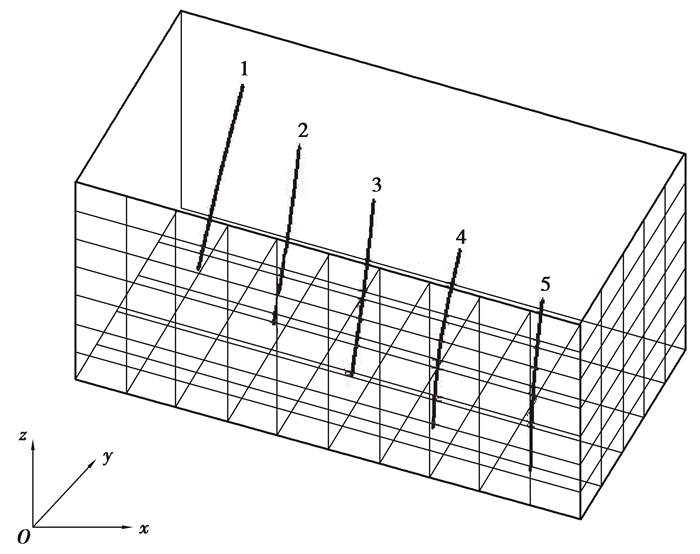
断层线(fault stick)是断层在深度域下平行剖面断层轮廓。通过提取每个勘探线剖面图中的断层线,即可得到断层的三维线框模型,如图 2所示。断层线数据是用一系列平行剖面轮廓线模拟断层形态,数据之间相互关联且无干扰,是地质与采矿部门常用的图件。
|
图 2 空间序列断层线 Figure 2 Spatial sequence fault stick |
对上述不同断层建模数据分析可知:断点数据较为稀疏,对于复杂断层形态难以构建;断层多边形数据通常存在数据重叠区域,因而基于断层多边形断层面重构方法具有一定局限性;断层线数据之间没有重叠数据干扰,数据质量一般优于断层多边形。通过数据分析比较,最终选择断层线数据作为断层面重构基础数据。
但由于经济因素制约,原始的勘探线剖面间距较大,提取的断层线过于稀疏,且断层形态复杂多变,因而拟合断层面不够合理和平滑。对此问题,笔者提出采用Morphing方法建立相邻断层线之间的过渡曲线,以实现稀疏断层线之间的光滑渐变。
2 Morphing方法介绍Morphing方法又称连续渐变技术,是指将源图像或几何图形光滑渐变到目标图像或目标几何图形,广泛应用于图像渐变、三维动画制作、工业设计、地质制图等领域[11-14]。在渐变过程中,中间帧既有源图像或几何图形的特征,又有目标图像或目标几何图形的特征。下面介绍利用Morphing方法构建相邻断层线过渡曲线方法。
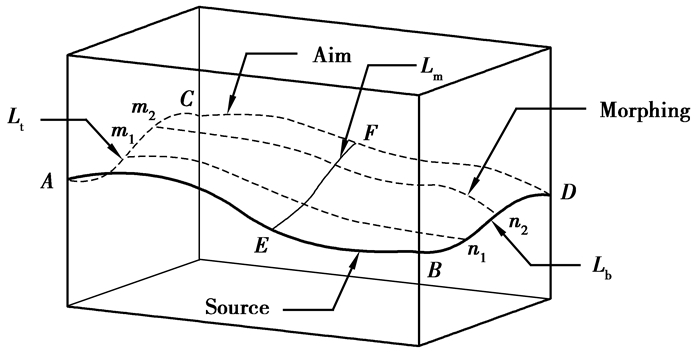
2.1 几何描述以图 3为例,AB、CD为2个断层线,设AB为起始断层线(Source),CD为目标断层线(Aim);AC、BD为断层线顶底约束线,设AC为顶约束路径(Lt),BD为底约束路径(Lb),若AC、BD中间有约束线EF,设EF为中间约束路径(Lm)。经过约束路径的约束,可实现从起始断层线到目标断层线的过渡,m1n1、m2n2即为中间过渡曲线(Morphing)。
|
图 3 Morphing方法示意图 Figure 3 Morphing method diagram |
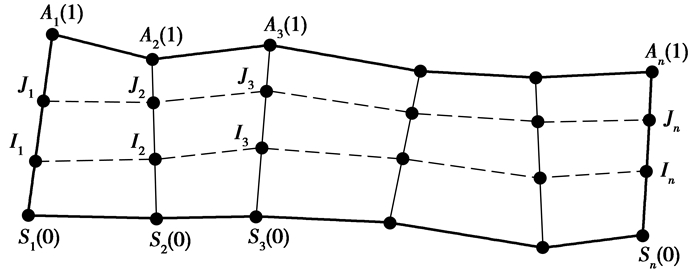
设起始断层线Source为连续函数S(x),0≤x≤1,S(0)为起点,S(1)为终点;目标断层线Aim为连续函数A(x),0≤ x ≤1,A(0)为起点,A(1)为终点。起始断层线Source和目标断层线Aim特征点相对应,建立对应点S(u)与A(u)之间关系,0≤u≤1,如图 4所示。
|
图 4 Morphing方法示意图 Figure 4 Morphing method diagram |
通常,断层线顶底无约束线,因此,可采用起始断层线和目标断层线对应起点和终点连线的直线段为约束路径。此时,建立路径插值函数:
| $ L(u, v)=(1-v)S(u)+vA(u), $ | (1) |
式中:v为比例参数(0≤v≤1),表示过渡曲线与起始断层线与目标断层线的相离程度,当v=0时,过渡曲线退化为起始断层线,v=1时,过渡曲线演变为目标断层线;L(u, v)为S(u)与A(u)之间对应的插值点。选取不同的比例参数v,即可得到一系列过渡曲线,如图 4中的曲线I(I1,I2,I3,…,In)和J(J1,J2,J3,…,Jn)。
2.3 特征点匹配正确实现特征点匹配是Morphing方法实现平滑过渡的关键问题之一。对于断层线数据,特征点包括断层与各个煤层顶底板的交点以及保证断层形态其余控制点。每条断层线可作为一个网络Gi(Vij,Pij),i代表不同剖面上断层线编号,j代表同一断层轨迹线上的特征点的序号。其中Vij={v0i, v1i, v2i,…,vni}表示断层与各个煤层顶底板的交点,Pij={p0i, p1i, p2i,…,pni}表示断层形态其余控制点。
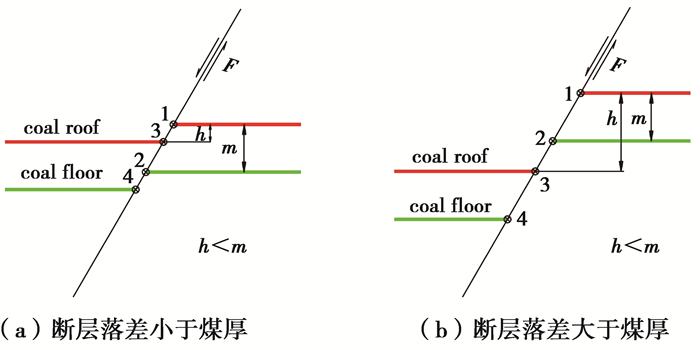
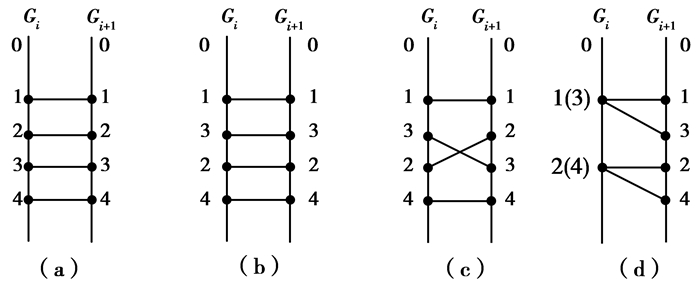
当仅存在Vij={v0i, v1i, v2i,…,vni}时,设同一断层下盘(上盘)顶、底板线与断层的交点编号分别为1、2,上盘(下盘)顶、底板线与断层的交点编号分别为3、4,如图 5所示。相邻断层线特征点对应关系可抽象成4种情况,如图 6所示。当断层落差大于煤厚,节点顺序对应,如图 6(a)所示;当断层落差小于煤厚,此时2号节点位于3号节点之下,节点对应关系如图 6(b)所示;当相邻断层落差介于(a)(b)情况中间,表示断层落差逐渐变小,节点对应关系如图 6(c)所示;当断层落差逐渐过渡为0,一侧断层线1号节点和3号节点退化为一点,2号节点和4号节点退化为一点,表示断层尖灭于地层,如图 6(d)所示。
|
图 5 煤层与断层接触关系 Figure 5 Contact relationship between coal seam and fault |
|
图 6 Vij特征点对应关系 Figure 6 Vij Feature point correspondence |
当Vij={v0i, v1i, v2i,…,vni},Pij={p0i, p1i, p2i,…,pni}同时存在时,可以看成在图 6中4种情况的基础上增加形态控制点。由于相邻断层线之间Pij控制点数目可能不一致,因此需要正确匹配控制点,以保证每条断层线之间都有特征点相匹配。
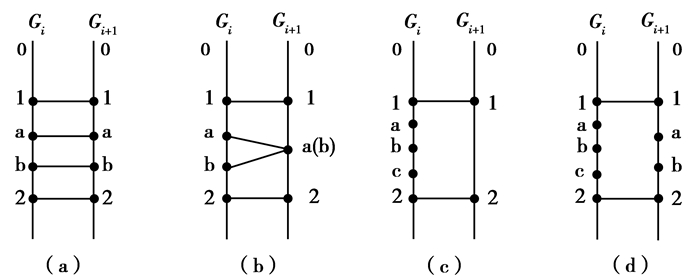
以Vij相邻节点为一单元进行研究。如图 7所示,特征点对应关系可抽象成一对一(图 7(a))、多对一(图 7(b))、多对0(图 7(c))、多对多(图 7(d))4种情况。对于(a)、(b)情况,可直接实现特征点匹配,对于(c)、(d)情况需要根据曲线的弯曲特征,进行特征点匹配。
|
图 7 Pij特征点对应关系 Figure 7 Pij Feature point correspondence |
为简化匹配难度,采用距离二分法以方式保证每条断层线Pij数量相等。现已知断层线上最多有k个Pij,G断层线有m(m < k)个Pij,则G断层线需要加k-m个点。为保证线段节点均匀分布,可通过比较G中每段线段长度,在较长的线段的中点处加点,进行k-m次二分,其过程如式(2)所示,以实现对距离的二分细化,使得每条断层线上的Pij实现一一对应。
| $ {\rm MAX}\left\{ {{l}_{1}}, {{l}_{2}}, \cdots, {{l}_{m+1}} \right\}\xrightarrow{1次二分}\\{\rm MAX}\left\{ {{l}_{1}}, {{l}_{2}}, \cdots, {{l}_{m+1}}, {{l}_{m+2}} \right\}\cdots \xrightarrow{k-m次二分}\left\{ {{l}_{1}}, {{l}_{2}}, \cdots, {{l}_{m+1}}, \cdots, {{l}_{k+1}} \right\}。$ | (2) |
当每条断层线中Gi(Vij,Pij)一一对应,特征点匹配工作完成。
3 断层尖灭位置确定研究区域内,断层末端可以分为不尖灭、两端尖灭、一端尖灭3种情况。对于末端存在尖灭的情况,需要对尖灭位置进行推测。根据大量野外实际观测发现,同一条断层在不同位置落差不尽相同且断层的走向长度与落差存在一定的比例关系[15-16]。这一比例关系通常通过实际数据统计分析获得。在没有实际数据时,可参考矿体尖灭位置推断方法,即有限外推法,来确定断层尖灭位置。
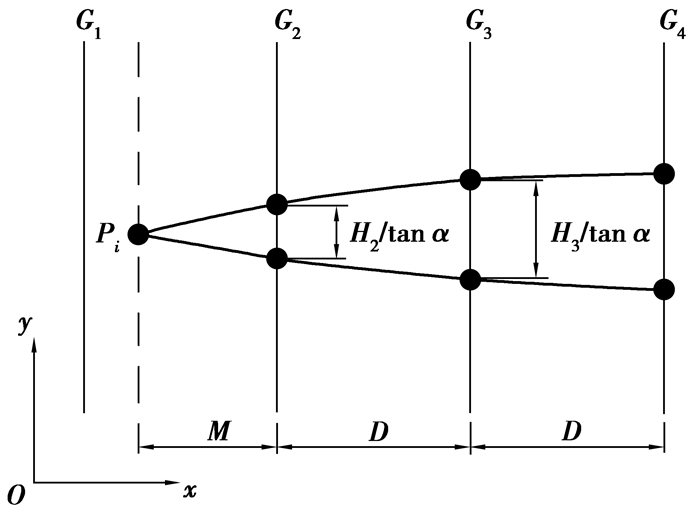
其原理如图 8所示。G2剖面上某一煤层层面出现断裂,在相邻G1剖面上未发现断裂,可以推断,在G2和G1剖面之间,断层尖灭到一点Pi。通常,断层尖灭点距边缘勘探线距离取相邻勘探线距离的1/2,1/3,1/4等等,而最常取1/2。实际中,断层尖灭终点的远近应考虑断层落差或平错的变化规律,即:当断层落差较大时,尖灭点应较远;断层落差较小时,对应的尖灭点距离边缘勘探线较近。
|
图 8 断层尖灭示意图 Figure 8 Fault thinning out diagram |
依据断层尖灭点距离与断层落差或平错的变化规律,可将断层尖灭点距离与落差或平错简化为近似的线性关系简化求解。设断层连续平稳过渡到尖灭点,断层尖灭点距离G2剖面距离为M,勘探线相邻距离为D,则有:
| $ \frac{M}{M+D}\approx \frac{{{H}_{2}}/\tan \alpha }{{{H}_{3}}/\tan \alpha }。$ | (3) |
化简得:
| $ M\approx \frac{{{H}_{3}}}{{{H}_{3}}-{{H}_{2}}}\cdot D, $ | (4) |
式中:H2,H3分别为G2和G3断层剖面上某一断层的落差;α为断层平均倾角。
4 相交断层切削断层面重构的主要内容还包括断层之间的切削处理。在复杂断层系统中,多条断层纵横交错,相互切割。对相交断层,应充分分析断层在走向方向和倾向方向的趋势,判断断层相交关系,对断层末端进行趋势延伸,实现断层之间的相交与组合。
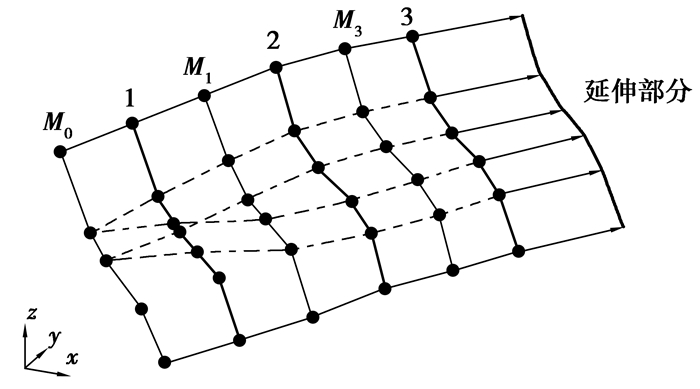
对于断层线数据,断层延伸方向主要为走向方向。断层末端趋势延伸应考虑断层的的整体趋势和局部特点。上文建立了每条断层线节点对应关系,因此,可以通过对应节点所连曲线进行趋势外推。如图 9所示,1,2,3为断层线,M0,M1,M2为中间过渡曲线(v=0.5),最右侧线条为延伸曲线。
|
图 9 曲线延伸示意图 Figure 9 Curve extension diagram |
采用简单有效,便于计算机实现的拉格朗日插值方法对曲线进行趋势外推。给定n+1个对应节点坐标(x0,y0,z0),(x1,y1,z1),…,(xn,yn,zn),横坐标两两不同,则曲线可以写成:
| $ \left\{ \begin{align} &{{L}_{n}}\left( x \right)=\sum\limits_{k=0}^{n}{{{l}_{k}}\left( x \right){{y}_{k}}}, \\ &{{Q}_{n}}\left( x \right)=\sum\limits_{k=0}^{n}{{{l}_{k}}\left( x \right){{z}_{k}}}, \\ \end{align} \right. $ | (5) |
其中:
| $ {{l}_{k}}=\prod\limits_{\begin{smallmatrix} i=0 \\ i\ne k \end{smallmatrix}}^{n}{\left( \frac{x-{{x}_{i}}}{{{x}_{k}}-{{x}_{i}}} \right)\left( k=0, 1, \cdots, n \right)}。$ | (6) |
Ln(x)曲线的建立相当于确定了曲线延伸方位角,Qn(x)曲线的建立相当于确定了曲线高程的变化趋势。
由于高次插值会发生龙格现象,即曲线出现左右震荡现象而使得拟合曲线偏离预期。因此,应尽量采用低次拉格朗日插值方法。延伸部分要兼顾断层面整体趋势和局部变化,一般选择要延伸部分末端对应的2个或3个节点建立曲线,用于外推。
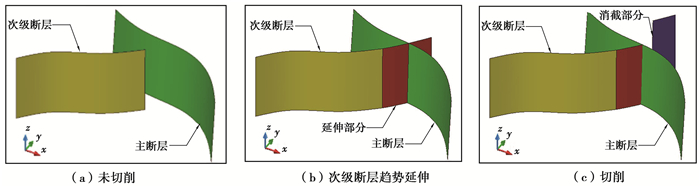
延伸距离选择不宜过长,距离越大,误差越大,略超过主断层即可,通过两断层面三角网求取交线,以交线为路径,削截超过主断层部分的次级断层部分,实现断层的相交处理,切削处理过程如图 10所示。
|
图 10 断层面切削处理示意图 Figure 10 Cutting surface treatment |
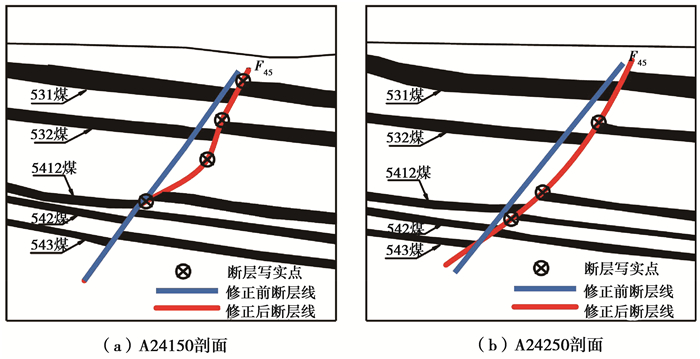
以扎哈淖尔露天矿首采区勘探线剖面图中提取的断层线为断层面重构基础数据,应用Morphing方法构建相邻断层线过渡曲线。如图 11所示,以F45为例,由于生产揭露数据的补充,发现原推断的断层形态局部发生突变:A24150勘探线F45号断层线由原来的“平直式”断层修正为“座椅式”断层,A24250勘探线F45号断层线由原来的“平直式”断层修正为“铲式”断层。断层形态的突变导致断层面重构之后的形态生硬,不符合实际断层发育趋势。
|
图 11 断层写实对比图 Figure 11 Fault realistic comparison chart |
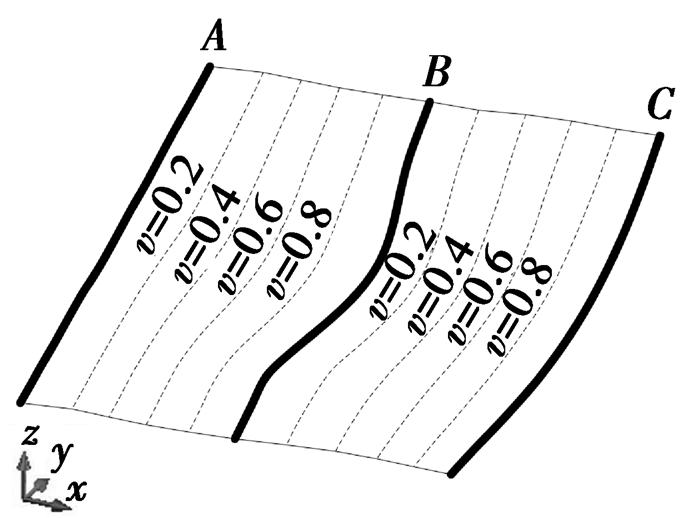
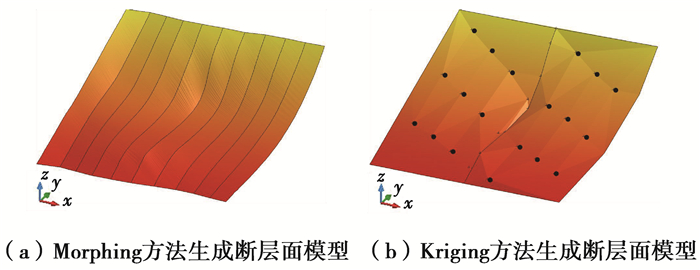
依据本文中介绍的Morphing方法,以具有自主知识产权的露天矿辅助设计软件SMCAD[17-18]为依托,基于.NET平台,针对AutoCAD进行二次开发,分别生成相邻断层线v=0.2,0.4,0.6,0.8位置处的过渡曲线,如图 12所示。利用CD-TIN生成断层面模型[19-21],通过对比Morphing方法生成的断层面形态和Kriging方法生成的断层面形态(图 13),可以发现通过Morphing方法构建相邻断层线过渡曲线,进而生成断层面CD-TIN模型,可以充分顾及断层处弯曲细节,更好地描述断层面空间形态。
|
图 12 过渡曲线生成 Figure 12 Transition curve generation |
|
图 13 断层面三维渲染图对比图 Figure 13 Comparison of fault plane morphology |
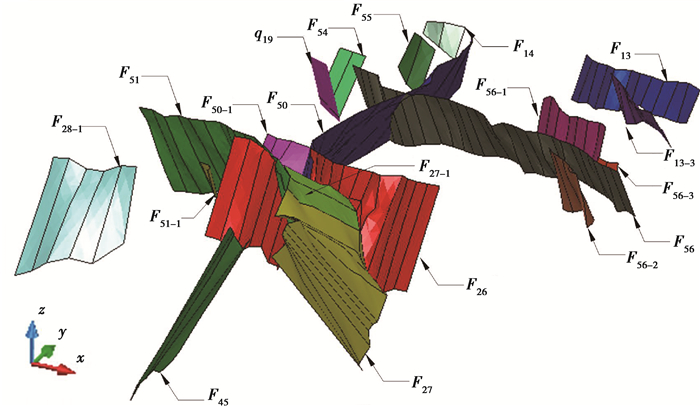
为进一步完整重构断层面空间形态,依据上文中介绍的断层尖灭位置确定方法和相交断层处理方法,对扎哈淖尔露天矿首采区境界内19条断层进行过渡曲线生成、尖灭位置推断、相交断层切削处理,最终构建了扎哈淖尔露天矿首采区境界内断层三维模型,如图 14所示。
|
图 14 露天矿首采区断层三维模型 Figure 14 3D model of fault in first mining area of open-pit mine |
1) 通过对比不同断层建模数据特征,最终选用无数据重叠干扰的断层线数据作为断层面重构基础数据。
2) 针对稀疏断层线数据构建断层面形态粗糙、不精确问题,提出基于Morphing方法构建相邻稀疏断层线过渡曲线,同时基于CD-TIN重构平稳光滑断层面的方法;并对比Morphing方法和Kriging方法生成断层面形态,验证了方法的可行性。
3) 为完整描述断层形态,采用有限外推法,确定了断层尖灭位置;采用拉格朗日插值方法对断层线节点曲线进行趋势外推,实现相交断层面切削;并最终构建了扎哈淖尔露天矿首采区境界内19条断层三维模型。
| [1] |
李增学. 煤炭地质学[M]. 北京: 煤炭工业出版社, 2009: 173-177.
LI Zengxue. Coal Geology[M]. Beijing: Coal Industry Press, 2009: 173-177. (in Chinese) |
| [2] |
胡明, 廖太平. 构造地质学[M]. 北京: 石油工业出版社, 2007: 110-134.
HU Ming, LIAO Taiping. Structural geology[M]. Beijing: Petroleum Industry Press, 2007: 110-134. (in Chinese) |
| [3] |
徐华, 武强, 李坤, 等.
三维地质模拟中不确定性分析方法[J]. 系统仿真学报, 2012, 24(4): 837–842.
XU Hua, WU Qiang, LI Kun, et al. Uncertain analysis on 3D geology modelling[J]. Journal of System Simulation, 2012, 24(4): 837–842. (in Chinese) |
| [4] | Wu Q, Xu H. An approach to computer modeling and visualization of geological faults in 3D[J]. Computer & Geosciences, 2003, 29(3): 503–509. |
| [5] | Wu Q, Xu H, Zou X K, et al. A 3D modeling approach to complex faults with multi-source data[J]. Computers & Geosciences, 2015, 77: 126–137. |
| [6] | Wu Q, Xu H, Zou X K. An effective method for 3D geological modeling with multi-source data integration[J]. Computers & Geosciences, 2005, 31(1): 34–43. |
| [7] |
朱良峰, 潘信, 吴信才, 等.
地质断层三维可视化模型的构建方法与实现技术[J]. 软件学报, 2008, 19(8): 2004–2017.
ZHU Liangfeng, PAN Xin, WU Xincai, et al. Construction method and actualizing techniques of 3D visual model for geological faults[J]. Journal of Software, 2008, 19(8): 2004–2017. (in Chinese) |
| [8] | Zhu L F, Pan X, Sun J Z. Visualization and dissemination of global crustal models on virtual globes[J]. Computers & Geosciences, 2016, 90(part A): 34–40. |
| [9] |
李兆亮, 潘懋, 杨洋, 等.
三维复杂断层网建模方法及应用[J]. 北京大学学报(自然科学版), 2015, 51(1): 79–85.
LI Zhaoliang, PAN Mao, YANG Yang, et al. Research and application of the three-dimensional complex fault network modeling[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2015, 51(1): 79–85. (in Chinese) |
| [10] |
王润怀, 李永树.
异源点集下三维断层建模方法[J]. 煤田地质与勘探, 2007, 35(5): 11–16.
WANG Ruihuai, LI Yongshu. 3D fault modeling on point sets from different sources[J]. Coal Geology & Exploration, 2007, 35(5): 11–16. (in Chinese) |
| [11] | Wolberg G. Image morphing:a survey[J]. The Visual Computer, 1998, 14(8/9): 360–372. |
| [12] |
明镜, 颜玫.
基于Morphing的三维地质界面生成[J]. 地理与地理信息科学, 2014, 30(1): 37–40.
MING Jing, YAN Mei. Three-dimensional geological surface creation based on Morphing[J]. Geography and Geo-Information Science, 2014, 30(1): 37–40. (in Chinese) |
| [13] | Gotsman C, Surazhsky V. Guaranteed intersection-free polygon morphing[J]. Computers & Graphics, 2001, 25(1): 67–75. |
| [14] | Albrecht S. A solution to the vertex correspondence problem in 2D polygon morphing[D]. Osnabruck: University Osnabruck, 2006: 11-22. |
| [15] |
赵宝良, 徐国堂.
预测"煤断层"的落差和走向长度的新方法[J]. 阜新矿业学院学报(自然科学版), 1996, 15(2): 174–176.
ZHAO Baoliang, XU Guotang. A new method predicting throw and strike-extended length of coal fault[J]. Journal of Fuxin Mining Institute(Natural Science), 1996, 15(2): 174–176. (in Chinese) |
| [16] |
宋忠航, 冯阳, 施龙青, 等.
矿井小断层延伸长度定量化预测在麻黄井田的应用[J]. 煤炭技术, 2015, 34(8): 58–60.
SONG Zhonghang, FENG Yang, SHI Longqing, et al. Application of extended length quantitative prediction of mine minor fault in Mahuang field[J]. Coal Technology, 2015, 34(8): 58–60. (in Chinese) |
| [17] |
刘光伟, 白润才, 付恩三.
SMCAD矿业工程软件在露天煤矿的应用[J]. 露天采矿技术, 2013(1): 74–78.
LIU Guangwei, BAI Runcai, FU Ensan. Application of SMCAD mining engineering software in open-pit coal mine[J]. Opencast Mining Technology, 2013(1): 74–78. (in Chinese) |
| [18] | Zhao H, Bai R C, Liu G W. 3D modeling of open pit based on AutoCAD and application[J]. Procedia Earth and Planetary Science, 2011, 3: 258–265. DOI:10.1016/j.proeps.2011.09.092 |
| [19] | Lee D T, Schachter B J. Two algorithms for constructing a delaunay triangulation[J]. International Journal of Computer and Information Sciences, 1980, 9(3): 219–242. DOI:10.1007/BF00977785 |
| [20] | Anglada M V. An improved incremental algorithm for constructing restricted Delaunay triangulations[J]. Computer & Graphics, 1997, 21(2): 215–223. |
| [21] | Gao Z, Yu Z, Holst M. Feature-preserving surface mesh smoothing via suboptimal Delaunay triangulation[J]. Graphical Models, 2013, 75(1): 23–38. DOI:10.1016/j.gmod.2012.10.007 |
 2018, Vol. 41
2018, Vol. 41


