岩石在变形破坏过程中,会有大量裂纹萌生、扩展以及断裂等,伴随着这些裂纹的发育,会产生以弹性波的形式释放岩石内部储存的能量的现象,这种现象就被称为岩石声发射[1-3]。由此可以看出声发射信号的产生与岩石变形破坏过程息息相关,它能够直观地反映岩石内部裂纹裂隙的发育程度以及岩石破坏程度[4],因此通过从不同的角度,利用不同的研究方法对声发射信号数据进行研究分析,能够更深入地了解岩石变形破坏的机制机理等信息。
分形理论是由Benoit B. Mandelbrot[5]在1975年正式创立的。1991年中国科学家谢和平院士[6]采用分形几何学与岩石损伤力学相结合的方法,将分形理论引入到岩石力学研究领域。目前,在岩石力学分形以及岩石声发射研究领域取得了一系列的研究成果[7-19]。吴贤振等[11]通过计算4种岩石在单轴压缩破坏条件下声发射能量频率的关联维数,得到了不同岩石声发射的分形特征,并研究了岩体失稳破坏的前兆信息;Kusunose等[12]对2种不同纹理分布的花岗岩进行了三轴压缩条件下声发射试验,并计算了声发射事件空间分布的分维值,发现岩石内部微裂隙的发育扩展和声发射事件的空间分布明显受到岩石纹理的影响;梁正召等[13]利用数值模拟软件模拟了岩石试件在单轴压缩条件下的破坏过程,研究了岩石在单轴压缩破坏过程中微破裂的分形特征。高保彬等[14-15]对同组的软煤和硬煤进行单轴压缩条件下的声发射试验,分别研究了煤样在单轴压缩条件下的声发射分形特征以及不同硬度条件下的煤样声发射分形特征的区别。在声发射RA值研究方面:日本学者Shiotani等[16]通过对比岩石弯曲与剪切试验的声发射信号,发现不同加载条件下声发射RA值具有很大差异,通过对比研究发现岩石在变形破坏过程中大小不同的声发射RA值对应不同种类的裂纹的产生,高RA值代表岩石内部产生的是张裂纹,而低RA值对应剪切裂纹的产生。Christian等[17]的研究也证明了这一点。国内的苗金丽等[18]、周子龙等[19]也利用这一结论,研究花岗岩在侧向扰动作用下发生岩爆时,岩爆发生的机理以及前兆。
随着采矿工程、石油开采以及隧道等岩体工程向深部发展,对高围压下的岩石力学及声发射特性的研究显得尤为重要。然而,作为在岩体工程中经常遇到的沉积岩之一——页岩,却少见有学者对能够反映其破坏机制的声发射RA值进行研究。因此,对页岩声发射RA值以及其分形特征进行研究,得到其分形特征和破裂前兆信息,并以此为工程实践提供理论支持显得很有必要性。
笔者通过不同围压条件下的常规三轴压缩声发射试验,研究揭示页岩声发射RA值及其分形特征的变化规律,以进一步了解和认识岩石的破坏过程及其机理,并为岩石破坏提出合理的前兆判据。
1 试验过程 1.1 试样的选取与制备本次试验所采用的岩样均取自重庆彭水两江桥头志留系罗惹坪组岩层的页岩。为了保证试验结果具有较小的离散性,试验所用的岩石试件都是从同一块完整性和均质性较好的S9号岩块上钻取的。试件加工严格按照国际岩石力学学会建议的方法进行,采用试件规格为ϕ50 mm×100 mm的圆柱体,试件表面光滑,无明显缺陷,并对其两端进行了磨平,不平行度控制在±0.02 mm以内,如图 1所示。

|
图 1 岩样照片 Figure 1 Photos of rock samples |
本次试验加载设备采用美国MTS815岩石液压伺服力学系统。该设备最大轴向加载载荷为2 800 kN,采用全数字计算机自动控制,可采用力、位移、轴向应变等多种加载方式并可进行高速数据采集,本设备具有测试精度高、性能稳定等优点。
声发射监测的设备则采用美国声学物理公司PAC生产的PCI-Ⅱ型声发射检测仪。该测试分析系统具有AE(acoustic emission)特征参数与波形同时采集,抗干扰能力和排除噪音能力强等技术特点。
1.3 试验步骤所进行的试验为常规三轴压缩全过程声发射试验。在试验过程中,保证荷载的加载和声发射的监测同步进行,并采集常规三轴压缩试验全过程中的声发射信号。试验系统如图 2所示。
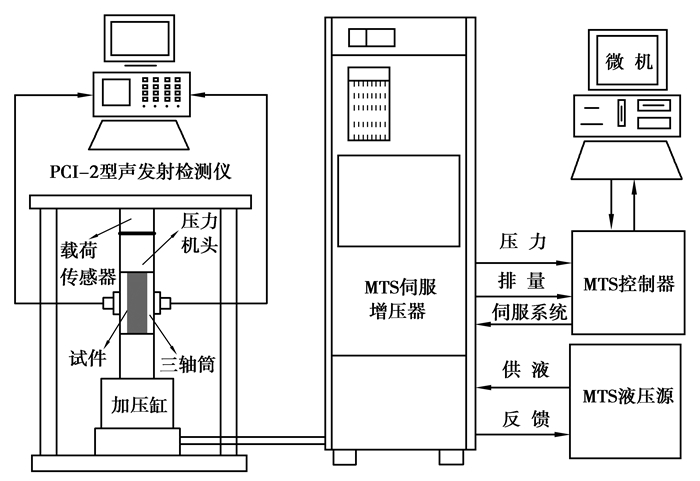
|
图 2 试验系统示意图 Figure 2 Schematic diagram of the test system |
首先,按照试验要求将岩石试件套上热缩管。然后按照伪三轴压缩试验的规定要求放置岩样试件后,在三轴筒外侧对称布置2个声发射探头,探头位于中部位置。为了保证探头与三轴筒接触良好,以黄油为耦合剂并用胶带将探头固定在三轴筒外壁。为消除环境噪声对声发射试验的影响,但又不至于丢失过多的声发射信号,试验时的声发射门槛值设置为30 dB。接下来以10 MPa/min的加载速率施加围压至预定值,并同时开始接收声发射信号,达到预定围压后,施加轴向载荷,并将其加载速率设置为0.1 mm/min,施加轴向荷载直至岩石试件破坏,并达到残余强度阶段,试验结束。具体岩石试件参数见表 1。
| 表 1 岩石试件参数 Table 1 Parameters of rock specimen |
声发射参数RA值是指声发射撞击上升时间与幅度的比值,单位为ms/dB。研究表明高RA值对应张裂纹,低RA值对应剪切裂纹,因此对其进行比较,可以分析页岩在常规三轴压缩条件下其破坏过程的微观机制[16-19]。如图 3所示,选取了3个典型页岩试件的试验数据,分别绘制岩样在不同围压下的主应力-时间-声发射RA值关系图。
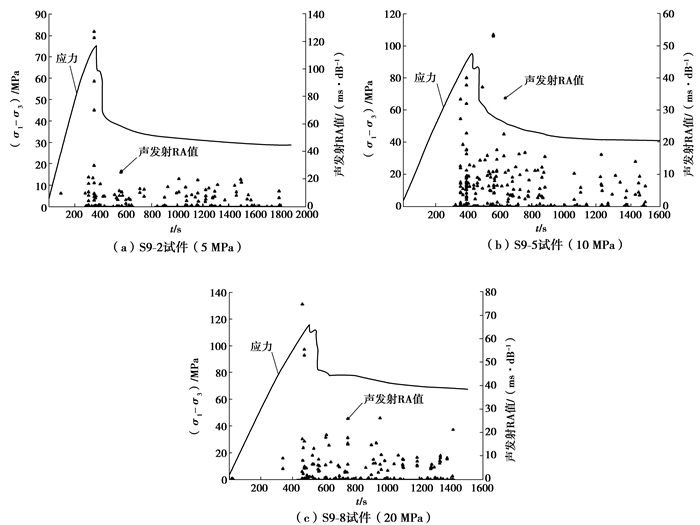
|
图 3 主应力-时间-声发射RA值关系曲线 Figure 3 Relationship curves of stress-time-AE RA |
通过对不同围压下的主应力-时间-声发射RA值关系曲线图对比分析可以发现:3种围压下,页岩试件的声发射RA值都是以20 ms/dB以下的低RA值为主,仅在岩石试件主破裂发生前后有少量高RA值出现,因此可以判断:在常规三轴压缩破坏过程中,页岩的裂纹为张剪复合裂纹,但是以剪切裂纹为主,仅在岩石发生主破裂前后产生了少量张裂纹。通过分析研究页岩在常规三轴压缩破坏过程中声发射RA值的变化规律,可以发现页岩在常规三轴压缩条件下的破坏过程为:当岩石内部的局部应力超过岩石的承载力之后,岩石内部发生剪切破坏,产生较小的剪切裂纹;随着轴向压力的持续增加,岩石内部的剪切裂纹大量产生,并在达到峰值强度前后出现了少量张裂纹;随着裂纹的持续扩展,最终融合贯通,产生宏观破裂面,最终岩石发生破坏;在残余变形阶段,由于围压以及轴向压力的存在,岩石内部的剪切破坏持续进行,但张拉破坏减少甚至消失,岩石在发生主破裂之后,内部产生的裂纹仍以剪切裂纹为主。
其次,对比3种围压下试件声发射RA值中高RA值与低RA值的变化趋势可以发现:低RA值的变化并不明显,但是高RA值的变化却比较大。随着围压的升高,高RA值的裂纹明显减少,RA值的最大值也有明显的下降。这说明,高围压能够限制岩石内部的张裂纹的产生,但是对剪裂纹的限制并不明显。
3 页岩声发射RA值分形特征 3.1 关联维数计算方法分形理论中表征分形特征的参数为分维值,而确定分维值的方法主要有:信息维数、盒维数以及关联维数等等。其中关联维数作为一种对系统的时间过程行为反应灵敏的分形维数,能够较好地反映系统的动力学特性[20-21],因此笔者采用基于G-P算法的关联维数。
以不同围压下页岩在三轴压缩破坏过程中的声发射RA值序列为研究对象,每一个声发射RA值序列对应一个容量为n的序列集。对于时间序列,采用时间差法重构相空间,即按间隔为τ从时间序列中区属作为矢量的分量,从而构造出一批矢量,即:
| $ {\mathit{\boldsymbol{X}}_i} = \left\{ {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_{i + \tau }}, {\mathit{\boldsymbol{x}}_{i + 2\tau }}, \cdots, {\mathit{\boldsymbol{x}}_{i + \left( {m-1} \right)\tau }}} \right\}, i = 1, 2, \cdots, N, $ | (1) |
式中:m为相空间维数;Xi为重构后的相空间中的矢量;τ为延迟时间;n为原时间序列的点数;N为重构后相空间矢量的个数,N=n-(m-1)τ。
关联维数计算公式为
| $ \left. {\begin{array}{*{20}{l}} {D = \mathop {\lim }\limits_{r \to 0} \left( {\ln C\left( r \right)/\ln r} \right)}\\ {C\left( r \right) = \frac{1}{{{N^2}}}\sum\limits_{i \ne j}^N {H\left( {r-|{x_i}-{x_j}|} \right)} } \end{array}} \right\}, $ | (2) |
式中:C(r)为关联函数;H(r)为Heavjiside函数,
相空间维数的大小在一定程度上会影响关联维数,为了确定合适的相空间维数,分别取m=2,3,4,5,6,7,8来计算关联维数,如图 4所示。从图 4中可以看出,当相空间维数m=6时,关联维数趋于稳定,因此,本文中相空间维数确定为6。
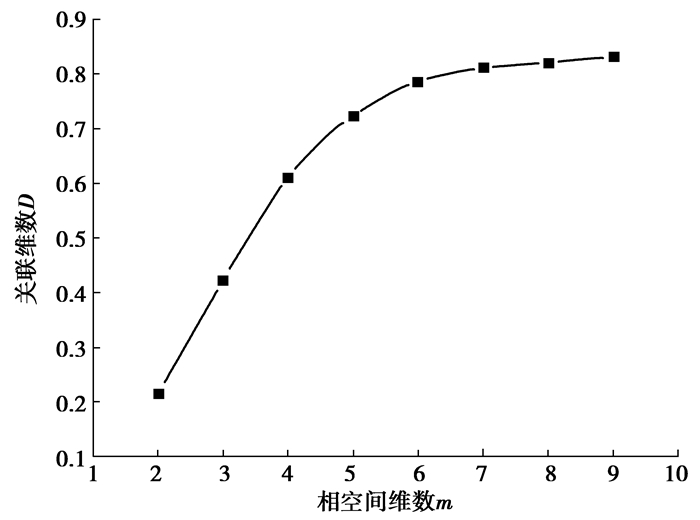
|
图 4 相空间维数m与关联维数D关系曲线 Figure 4 Relationship curve of phase space dimension (m) and correlation dimension (D) |
如图 5所示为k=0.2,0.4,0.6,0.8,1.0,1.2的关联维数拟合曲线,从图 5中可以看出,在3种围压下,声发射RA值的相关性系数分别为:0.956 5,0.951 4,0.977 6,相关性系数均大于0.95,表明页岩声发射RA值在时间序列上具有分形特征。
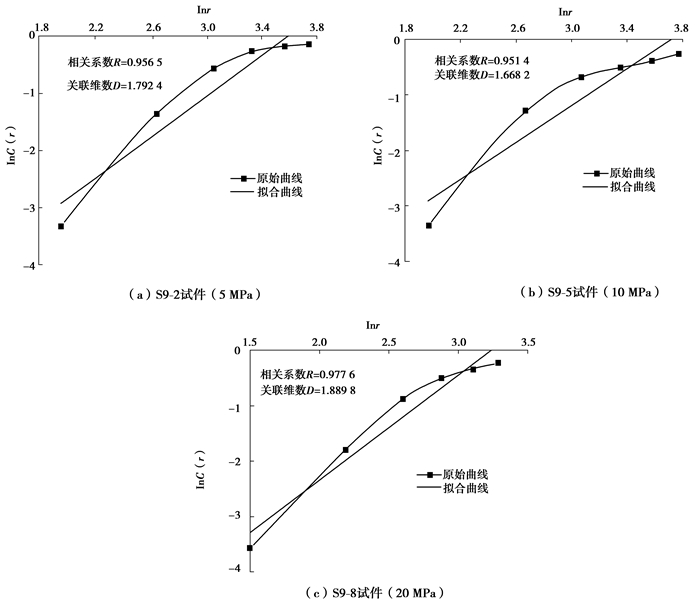
|
图 5 关联维数拟合曲线 Figure 5 Fitting curves of correlation dimension |
结合以上总结的关联维数的计算公式,并利用MATLAB软件编程关联维数的计算程序,分别计算页岩在不同围压下在常规三轴压缩破坏的过程中声发射RA值的关联维数,得到声发射RA值关联维数与时间的关系曲线,如图 6所示。为了更清晰的表示分形维数的变化趋势,对原始曲线进行了平滑处理,在图 6中以红色虚线表示。
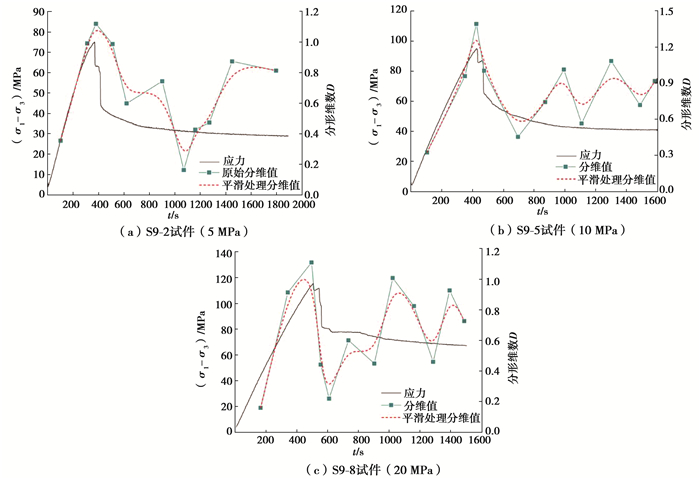
|
图 6 分形维数与时间的关系曲线 Figure 6 Relationship curves between fractal dimension and time |
从图 6中可以看出,虽然围压不同,但是声发射RA值的关联维数变化规律基本上是一致的,都是在加载初期持续上升,并在达到峰值强度前后关联维数也达到峰值,随之是一个突降,在残余强度阶段,关联维数出现了明显了波动,并且围压越高,波动越明显。这说明,页岩在常规三轴压缩破坏过程中分形维数的演化模式为:上升—突降—波动。
根据分形理论[6, 20-22]以及大量研究[11-15, 23]可知,对于时间序列上的混沌系统,分形维数的持续上升表明系统内小事件占大多数并且系统处于无序不确定的发展状态;分形维数的下降表明系统内大事件增多并且系统开始朝着有序的确定的方向发展。因此,结合页岩声发射RA值的分布以及分形维数的变化规律可知:在岩石试件达到峰值强度之前,岩石内部的裂纹处于无序扩展的状态,在加载初期,岩石内部产生了大量微小的剪切裂纹,这些裂纹此时处于无序发展状态,随着荷载的持续增大,岩石内部的小裂纹开始融合贯通,形成了较大的破裂面,裂纹的发展也由之前无序的状态转变为有序的沿破裂面发展的状态,直至宏观破裂形成,分形维数也降到了极小值,这预示着岩石即将发生破坏,因此可以将分形维数的首次突降作为岩体失稳破坏的前兆。
从三幅图中可以看出,在岩石试件的残余变形阶段,分形维数出现了上升—下降—上升—下降的循环波动,结合这一阶段声发射RA值的情况可以看出:在残余变形阶段,岩石试件内部裂纹的发展仍在持续进行,并且十分活跃。此阶段的变化过程为:在试件发生主破裂之后,由于围压以及轴向荷载的存在,试件内部的裂纹继续发育扩展,此时分形维数有小幅上升,说明试件内部的一部分还未形成宏观破裂面的小裂纹继续无序扩展,最后融合贯通,形成新的较小的宏观破裂面,此时分形维数达到一个小的峰值,然后出现下降,说明岩石内部宏观破裂面正有序的扩展形成宏观裂纹。接着新的小裂纹又开始融合贯通,形成破裂面,如此反复进行,直至外部荷载不足以使内部裂纹继续扩展融合,达到稳定状态,试验结束。因此可以认为岩石在残余变形阶段裂纹的演化模式为:小裂纹扩展—融合贯通形成破裂面—沿破裂面形成宏观裂纹的循环模式。
4 结论经过对页岩在常规三轴压缩破坏过程中的声发射RA值以及声发射RA值的分形特征进行分析研究之后,可以得到以下结论:
1) 页岩在三轴压缩破坏过程中的裂纹为张剪复合裂纹,以剪切裂纹为主,仅在主破裂发生前后产生少量张裂纹。并且随着围压的升高,张裂纹明显减少。
2) 页岩声发射RA值在时域上具有自相似特征,具有分形特征,其分形特征演化模式为:上升—突降—波动。
3) 页岩内部在加载初期,形成大量小的剪切裂纹,这些裂纹在初期无序发展,此时分形维数逐渐上升,并达到峰值,随着裂纹的扩展,裂纹之间相互融合贯通,形成破裂面,此时分形维数发生突降,说明,岩石内部裂纹开始沿着破裂面有序发展,直至产生宏观裂纹,预示着岩石即将发生破坏,因此,可以将分形维数的首次突降作为岩体失稳破坏的前兆。
4) 在残余变形阶段,分形维数处于波动状态,岩石内部的裂纹不断的发展融合,形成较小的破裂面,然后形成宏观裂纹,然后继续发展融合,反复进行,直至外部荷载不足以使内部裂纹继续扩展融合,达到稳定状态,试验结束。
| [1] |
蔡美峰, 何满潮, 刘东燕. 岩石力学与工程[M]. 北京: 科学出版社, 2002.
CAI Meifeng, HE Manchao, LIU Dongyan. Rock mechanics and engineering[M]. Beijing: Science Press, 2002. (in Chinese) |
| [2] |
秦四清, 李造鼎, 张倬元, 等. 岩石声发射技术概论[M]. 成都: 西南交通大学出版社, 1993.
QIN Siqing, LI Zaoding, ZHANG Zhuoyuan, et al. An introduction to acoustic emission technology on rocks[M]. Chengdu: Southwest Jiaotong University Press, 1993. (in Chinese) |
| [3] | Karakus M, Perez S. Acoustic emission analysis for rock-bit interactions in impregnated diamond core drilling[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 68: 36–43. DOI:10.1016/j.ijrmms.2014.02.009 |
| [4] |
李核归, 张茹, 高明忠, 等.
岩石声发射技术研究进展[J]. 地下空间与工程学报, 2013, 9(1): 1794–1804.
LI Hegui, ZHANG Ru, GAO Mingzhong, et al. Advances in technology of acoustic emission of rock[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(1): 1794–1804. (in Chinese) |
| [5] | Mandelbrot B B. Fractals:forms, chance and dimension[M]. San Francisco: W H Freeman, 1977. |
| [6] |
谢和平. 分形-岩石力学导论[M]. 北京: 科学出版社, 1996: 136-137.
XIE Heping. An introduction to fractal rock mechanics[M]. Beijing: Science Press, 1996: 136-137. (in Chinese) |
| [7] |
王泽鹏, 顾义磊, 房局, 等.
粒度对砂岩力学及声发射特性的影响研究[J]. 地下空间与工程学报, 2017, 13(S2): 705–714.
WANG Zepeng, GU Yilei, FANG Ju, et al. Research on damage mechanism and acoustic emission characteristics of sandstone with different granularity under loading[J]. Chinese Journal of Underground Space and Engineering, 2017, 13(S2): 705–714. (in Chinese) |
| [8] | Lei X L, Kusunose K, Nishizawa O, et al. Quasi-static fault growth and cracking in homogeneous brittle rock under triaxial compression using acoustic emission monitoring[J]. Journal of Geophysical Research, 2000, 105: 6127–6139. DOI:10.1029/1999JB900385 |
| [9] | Biancolinia M E, Bruttia C, Paparob G, et al. Fatigue cracks nucleation on steel, acoustic emission and fractal analysis[J]. International journal of fatigue, 2006, 28(12): 1820–1825. DOI:10.1016/j.ijfatigue.2005.12.003 |
| [10] | Zhang Z Z, Gao F, Shang X J. Rock burst proneness prediction by acoustic emission test during rock deformation[J]. Journal of Central South University, 2014, 21(1): 373–380. DOI:10.1007/s11771-014-1950-3 |
| [11] |
吴贤振, 刘祥鑫, 梁正召, 等.
不同岩石破裂全过程的声发射序列分形特征试验研究[J]. 岩土力学, 2012, 33(12): 3561–3569.
WU Xianzhen, LIU Xiangxin, LIANG Zhengzhao, et al. Experimental study of fractal dimension of AE serials of different rocks under uniaxial compression[J]. Rock and Soil Mechanics, 2012, 33(12): 3561–3569. (in Chinese) |
| [12] | Kusunose K, Lei X L, Nishizawa O, et al. Effect of grain size on fractal structure of acoustic emission hypocenter distribution in granitic rock[J]. Physics of the Earth and Planetary Interiors, 1991, 67(1/2): 194–199. |
| [13] |
梁正召, 唐春安, 唐世斌, 等.
岩石损伤破坏过程中分形与逾渗演化特征[J]. 岩土工程学报, 2007, 29(9): 1386–1391.
LIANG Zhengzhao, TANG Chun'an, TANG Shibin, et al. Characteristics of fractal and percolation of rocks subjected to uniaxial compression during their failure process[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1386–1391. (in Chinese) |
| [14] |
高保彬, 李回贵, 刘云鹏, 等.
单轴压缩下煤岩声发射及分形特征研究[J]. 地下空间与工程学报, 2013, 9(5): 986–991.
GAO Baobin, LI Huigui, LIU Yunpeng, et al. Study of acoustic emission and fractal characteristics of coal rock under uniaxial compression[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(5): 986–991. (in Chinese) |
| [15] |
高保彬, 李回贵, 李林, 等.
同组软硬煤煤样声发射及分形特征研究[J]. 岩石力学与工程学报, 2014, 33(2): 3498–3504.
GAO Baobin, LI Huigui, LI Lin, et al. Study of acoustic emission and fractal characteristics of soft and hard coal samples with same group[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 3498–3504. (in Chinese) |
| [16] | Shiotani T, Ohtsu M, Ikeda K. Detection and evaluation of AE waves due to rock deformation[J]. Construction and Building Materials, 2001, 15(5): 235–246. |
| [17] | Christian U G, Masayasu O. Acoustic emission testing[M]. Berlin: Springer Berlin Heidelberg, 2008. |
| [18] |
苗金丽, 何满潮, 李德建, 等.
花岗岩应变岩爆声发射特征及微观断裂机制[J]. 岩石力学与工程学报, 2009, 28(8): 1593–1603.
MIAO Jinli, HE Manchao, LI Dejian, et al. Acoustic emission characteristics of granite under strain rockburst test and its micro fracture mechanism[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1593–1603. (in Chinese) |
| [19] |
周子龙, 李国楠, 宁树理, 等.
侧向扰动下高应力岩石的声发射特性与破坏机制[J]. 岩石力学与工程学报, 2014, 33(8): 1720–1728.
ZHOU Zilong, LI Guonan, NING Shuli, et al. Acoustic emission characteristics and failure mechanism of high-stressed rocks under lateral disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(8): 1720–1728. (in Chinese) |
| [20] |
朱华, 姬翠翠. 分形理论及其应用[M]. 北京: 科学出版社, 2011.
ZHU Hua, JI Cuicui. Fractal theory and its application[M]. Beijing: Science Press, 2011. (in Chinese) |
| [21] |
孙洪泉. 分形几何与分形插值[M]. 北京: 科学出版社, 2011.
SUN Hongquan. Fractal geometry and fractal interpolation[M]. Beijing: Science Press, 2011. (in Chinese) |
| [22] |
吕金虎. 混沌时间序列分析及应用[M]. 武汉: 武汉大学出版社, 2002.
LU Jinghu. Chaos time series analysis and application[M]. Wuhan: Wuhan University Press, 2002. (in Chinese) |
| [23] |
张黎明, 任明远, 马绍琼, 等.
大理岩卸围压破坏全过程的声发射及分形特征[J]. 岩石力学与工程学报, 2015, 34(1): 2862–2867.
ZHANG Liming, REN Mingyuan, MA Shaoqiong, et al. Acoustic emission and fractal characteristics of marble during unloading failure process[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 2862–2867. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41



