1b. 辽宁工程技术大学 煤炭资源安全开采与洁净利用工程研究中心, 辽宁 阜新 123000;
2. 神华新疆能源黑山露天矿, 新疆 托克逊 838100
1b. Research Center of Coal Resources Safe Mining and Clean Utilization, Liaoning Technical University, Fuxin 123000, Liaoning, P. R. China;
2. Heishan Open Pit Mine, Shenhua Xingjiang Energy Co. Ltd., Toksun, Xingjiang 838100, P. R. China
露天矿路径优化是在满足一定的物理和经济约束之下求解露天矿运输道路网络最短路径的组合优化问题[1],长期以来一直作为露天矿物料流规划[2-3]以及卡车调度等研究领域[1]的重要分支,伴随着通信与交通运输学科的发展,先后形成了一系列较为成熟的、基于网络静态权值优化的方法体系与优化算法,这些方法现阶段被广泛的应用于露天矿山这类特殊的封闭道路网络系统中,并建立了以等效路径为确定权值的静态网络最短路分析理论体系。早期的大多数露天矿运输系统优化方法均建立在该理论体系基础上,如文献[4-7]等提出基于最小化运输费用成本的目标优化模型,此类算法从优化总体费用出发优化费用组成,在实际工程中较之人工方案具有显著的经济优势,但仍存在一定缺陷,原因在于未考虑道路费用动态随机性且难以实现预测的特点,并有部分学者为简化问题限制了节点间的费用权重,导致仍在以静态方法近似分析、规划具有波动成本的运输系统;又如文献[7-10]等先后提出基于节点距离最短的仿生学路径优化算法,此类算法在优化执行效率的同时均能起到明显的静态优化作用,但优化目标仅围绕几何距离和最短,未考虑对于矿山运输系统全局节点距离和最小化与费用成本最小化并不等效。
综合上述报道,所述算法均能得到当前目标条件下的最优解,但所述目标的差异导致优化结果往往无法得到实际的全局最优解,现阶段采用的优化手段均存在如下三方面的问题:①采用等效路径或运输功为目标函数进行的最优化求解,均未考虑随道路运输的能耗变化,所获得的解可以保证等效距离和最小,却无法保证能耗费用最低;②道路网络运输成本受路面质量、车型、车的载重量、道路坡面、司机驾驶技术、瞭望条件等限制,故网络节点间费用是受多种外源条件约束且随时间波动的,运输规划理应从能耗或成本费用入手建立目标;③直接采用确定费用权重简化求解所获得的最优解与实际动态场景中的费用成本最优化没有等效关系。
近年来,不断有学者论述采用确定权重静态分析运输及通信网络的现实不可行性,研究热点逐渐从静态、确定权问题转向变权重的动态随机网络求解问题上,从波动的动态网络耗费出发规划全局能耗最短路径。如文献[11]在论证传统的静态权值网络在实际的ITS(智能交通系统)、计算机网络以及通信的应用中存在缺陷的同时,进一步探讨了时变随机网络最短路径问题的求解方法;文献[12]应用理论证明的方法证明了传统最短路径算法在实际工程应用中的不适应性,且常无法获得正确的最优解,并提出改进的Dijkstra算法;又如文献[13]中建立了依赖时间的权重变量,并提出应用概率统计思想解算最短路径问题的新方法。
时变权重动态网络分析方法在实际网络中极具现实意义,在其他领域的研究报道较多,但在国内外露天矿道路优化文献中鲜有报道,故笔者在总结前人算法基础上,旨在研究基于权重动态变化条件下的最短路径求解问题,从露天矿道路网络运输功定义出发探索动态条件下时变运输功计算方法,并从概率统计角度建立最短路径问题的随机最优化求解模型,并进一步提出基于改进遗传算法的最短路径问题求解方法。
1 问题分析与模型构建 1.1 数学优化模型构建基于运输功最小化的露天矿路径分析问题可描述为:在露天矿运输道路网络系统中,自源节点A(露天采场剥离工作面节点)至目的节点B(露天矿排土工作面节点),动态搜索出一条目标路径满足其在整个调运周期内全局运输功最小。该问题是在满足物理和经济条件约束下,考虑道路网络弧段(边)权重动态变化的组合优化问题,旨在优化整个调运周期内总体运输成本。
假设某露天矿道路网络中有n个节点,整体的道路网络可表示为G{V, E, F, ΔH},G{V, E, F, ΔH}其中为非空节点集合V={1, 2, 3, …n};E为网络弧(边)集合,i, j节点间构成的弧段为ei, j=(i, j)∈E;F为弧段间卡车行驶阻力估计函数集合,ΔH为弧段间表征势能变化的高程差集合。网络模型中的可行解路径可表述为:在有限节点、有限弧段(边)的道路网络中,存在从源节点S到目的节点D不唯一走行方案,其中第k方案路径中两相邻节点间的有效路径表示为rk(i, j),网络中全部方案的可行路径解集可表示为R(s, d),可行路径解集中的所有路径表示为r1(1, 2), r2(2, 3), …, rn-1(n-1, n)。根据露天矿运输功的定义,网络中的路径方案的弧段总时变运输功可以表示为如下的线性表达:
| $ W = \sum\limits_{i = 1}^n {{F_{{e_{i, j}}}}} \;\Delta {S_{ij}} \cdot \Delta {L_{{e_{i, j}}}} + \sum\limits_{i = 1}^n {\Delta {h_{{e_{i, j}}}}} \cdot {S_{ij}} \cdot G, $ | (1) |
| $ {W_{\min }} = {\rm{Min}}\left( W \right) = {\rm{Min}}\left( {\sum\limits_{i = 1}^n {{F_{{e_{i, j}}}}} \cdot {S_{ij}} \cdot \Delta {L_{{e_{i, j}}}} + \sum\limits_{i = 1}^n {\Delta {h_{{e_{i, j}}}}} \cdot {S_{ij}} \cdot G} \right)。$ | (2) |
其中:式(1)中W表示克服阻力以及提升势能而产生的时变总运输功;式(2)为全局时变总运输功的最优化模型,其建立了在以最小化时变总运输功为目标函数的规划模型上;式(3)为路径状态决策变量;式(4)、(5)为模型约束;ΔLei,j表示弧段(边)的欧几里德距离,m;Δhei,j表示弧段(边)高程差,m;Fe表示车辆的行驶阻力(由Ff滚动阻力、Fr坡度阻力以及Fw空气阻力三部分组成),kN,该变量具体计算方法[14]见式(4)。其中G表示载重量,kg;f表示滚动阻力系数;r表示坡度阻力系数;α表示坡度;C表示空气阻力系数;A表示迎风面积,m2;ρ表示空气密度,kg/m3;v表示风速;v表示车辆的平均行驶速度。由式(1)~ (5)可知运输功是关于运输道路条件以及运行时间的动态表达。
| $ {S_{ij}} = \left\{ \begin{array}{l} 0\;\;\;{V_i}, {V_j} \notin \;R\left( {s, d} \right), \\ 1\;\;\;{V_i}, {V_j} \in \;R\left( {s, d} \right), \end{array} \right. $ | (3) |
| $ \begin{array}{l} {F_{\rm{e}}} \approx \left( {{F_{\rm{f}}} + {F_{\rm{r}}}} \right) + {F_{\rm{w}}} = f \cdot G \cdot \cos \alpha + r \cdot G + \left( {1/2} \right) \cdot C \cdot A \cdot \rho \cdot {v^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {f + r} \right) \cdot G + C \cdot A \cdot {{\bar v}^2}/21.15, \end{array} $ | (4) |
| $ \bar v = \Delta {L_{{e_{i, j}}}}/\Delta t。$ | (5) |
在实际运输道路网络中,由式(1)可知路径间的运输功权重均为时变的、不确定的,但在不同的路段条件下,时变运输功是严格依赖时间变量的,其统计规律很容易通过一定的统计分析手段获得,故整个优化模型可建立在随机过程基础之上考虑该问题。假定t是定义在t∈[t0, tm]闭区间上,将Ω={W1(t), W2(t),…,Wn(t)}作为依赖时间变量的n维随机变量,故其联合概率密度估计可表述为式(6),联合分布可表述为式(7):
| $ f\left\{ {{W_1}\left( t \right), {W_2}\left( t \right), \cdots, {W_n}\left( t \right)} \right\}, $ | (6) |
| $ F = \int { \cdots \int {f\left( {{W_1}\left( t \right), {W_2}\left( t \right), \cdots, {W_n}\left( t \right)} \right)} } \cdot {\rm{d}}{W_1}\left( t \right), \cdots {\rm{d}}{W_n}\left( t \right)。$ | (7) |
根据上述模型,假设优化场景:如果从A地到B地共有u条有效路径,其中任意路径γ的总运输功低于其他路径的概率可表示为:
| $ \begin{array}{l} \;\;\;\;\;\;\;F\left( {{W_1}, {W_2} \cdots {W_u}} \right) = {P_\gamma }\left( {{W_\gamma } \le {W_1}, \cdots, {W_\gamma } \le {W_u}} \right) = \\ \int {G\left( {{W_\gamma } \le {W_1}, \cdots, {W_\gamma } \le {W_u}} \right), \cdots, \int {f\left( {{W_1}, \cdots, {W_u}} \right) \cdot {\rm{d}}{W_1}, \cdots, {\rm{d}}{W_u}} } 。\end{array} $ | (8) |
通过建立如式(8)的最优化概率估计模型,运输网络的动态优化结果将完全依赖于变量的概率估计结果,即在场景中绝对优势路径在概率估计模型中估计值也相对较大,其反映的信息是现实场景下该路径的时变运输功总和全局最小。
2 基于改进GA的路径优化算法设计 2.1 个体编码设计假设某有效路径γ中共有7个节点,其源节点编号为14,目的节点编号为27,则该条路径可被编码为式(9)形式。
| $ {X_\gamma } = \left\{ {{\chi _1}, \cdots, {\chi _7}} \right\} = \left\{ {14, 16, 17, 19, 23, 25, 27} \right\}。$ | (9) |
由于遗传算法无法直接对现实问题进行优化求解,需要建立关于实际问题与算法解空间的一个映射[15-28],故遗传算法引入生物界种群的概念,通过创建差异性染色体个体实现现实问题可能解在算法求解空间的初始化映射。
种群初始化是确保种群中个体倾向多样性优质种群方向发展的前提,为增强种群个体质量且具有更好的多样性,增强算法鲁棒性,文中初始化种群过程采用有针对性的启发式策略以减少传统随机生成方法产生的索引开销,提高效率的同时,避免了入选路径出现回路,其初始化执行步骤可以描述为:
步骤1 假设运岩卡车在全路段匀速状态命题成立,认为运输功与路段间的欧氏距离成正比,并将道路网络弧段的欧式距离作为经验知识,赋值给路网弧段,作为路段先验经验,其中节点序号递增时权值为正,否则权值为负,以确保目标路径朝目标节点方向发展;
步骤2 将源节点作为染色体的第一个基因位,并执行如下操作完成第二个基因位的索引:
① 搜索有向图中与该节点相联系的正权值弧段中出度大于1的节点;
② 将正向弧段经验权的极小值者的后向节点作为第二个基因位填入染色体;
③ 标记②已经优选出的弧段;
步骤3 剔除被完成索引的弧段及节点,避免重复路径枚举,并以步骤2中的索引方式继续向下索引;
步骤4 按照此权值极小化方法快速枚举出全部的出度非1节点,建立多样性规模种群。
2.3 适应度评价与选择算子自然选择的作用是保留下适应环境的最优者,淘汰次优者,而在遗传算法中基于适应值函数的优化选择就起到此种自然法则的作用,通过将适应值作为指标,约束种群繁衍过程中高品质基因个体的规模,以选择机制的筛选形式控制整个种群的基因质量,提高算法在潜在最优解邻域内的寻优能力。
文中建立以最小时变运输功为目标的优化问题,理想最优解应为目标路径全局时变运输功总和最小。但文献[29]中已论证在大型网络中此种动态随机网络的解算中,欲获得一个有效的解往往十分困难,属于NP(Non-deterministic Polynomial)难问题。因此,为解决该问题,引用文献[29]中论证的概率统计学性质[30], 如式(10)所示,即路段能耗期望值越小,成为最优路段的可能性反而越大,并定义适应值函数为当前路径全局时变总运输期望的倒数,函数形式如式(11)。
| $ \sum {E\left( {{W_i}} \right) < \sum {E\left( {{W_j}} \right) \to {P_i} > {P_j}} }, $ | (10) |
| $ M\left( {{W_i}} \right) = 1/E\left( {{W_i}} \right)。$ | (11) |
种群中个体的M值越大,则表示该路径在整个路网的优化过程中越有可能成为动态路网中的最短路径。
为尽可能保留父代中的最佳个体,采用以适应值为指标的精英选择策略结合轮盘赌选择法对整个种群进行选择,具体步骤如下:
步骤1 在种群中优先选出种群个体中适应度最为优秀的ε%,作为种群的精英个体直接复制到下一代种群中;
步骤2 分别计算剩余种群中个体的适应度,根据
步骤3 采用轮盘赌选择法,统计累计概率区间,创建随机数γ∈[0, 1],保证随机数总量与剩余种群相同,模拟轮盘赌行为;
步骤4 根据
为进一步提高算法自身的随机搜索能力,遗传算法中有针对性的引入了交叉和变异操作,交叉在一定程度了上扩展了算法在带有先验条件下最优解的邻域范围,而变异则促使算法能更快速收敛于最优解,同时经过交叉和变异操作也进一步扩展了目标种群的多样性。
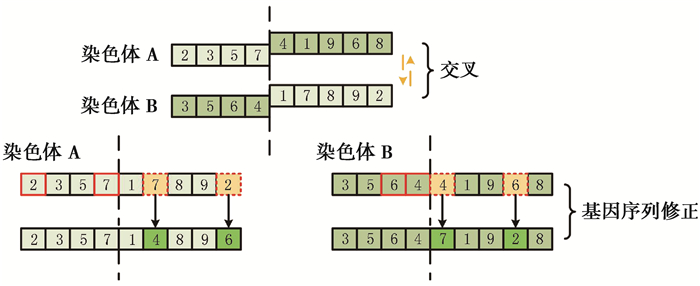
初始化种群保证了种群中均具有相同的源节点和目的节点基因,文中对种群中的个体采用单点交叉的方法进行处理,但由于单点交叉的随机性,当父代缺少相同基因位时有可能会产生非法个体,因此需要对非法个体进行修正,当存在如图 1所示的重复交叉错误时,应进一步按照初始种群中的启发策略进一步修改,具体修改过程如图 1所示。本文中具体的修正方法仍采用初始化种群过程中的启发式方法,启发获得2个确定的基因位路径,并修正子代中的缺失节点间的染色体序列。
|
图 1 染色体A与染色体B交叉及序列修正过程示意图 Figure 1 Cross and sequence modification between A and B |
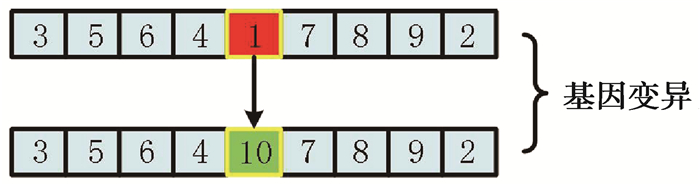
变异运算采用控制两个随机数进行,第一个随机数作为插入位,而第二个随机数作为基因位,对于每一个个体进行上述操作,最后即可得到变异种群,具体变异基因位的控制过程如图 2所示。
|
图 2 染色体基因组变异示意图 Figure 2 Chromosome genome variation |
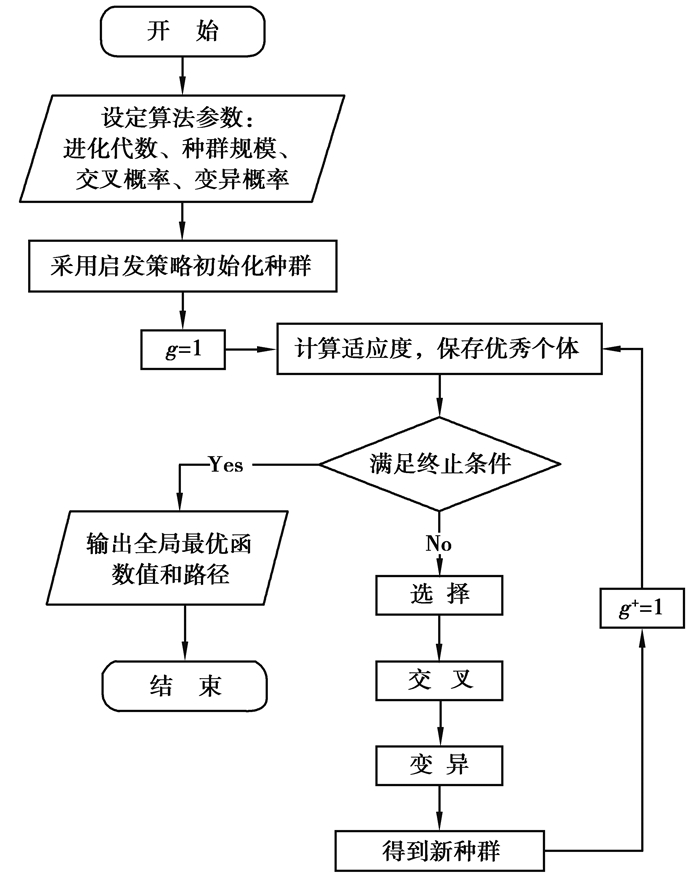
改进遗传算法整体实现流程如图 3所示。
|
图 3 改进遗传算法流程 Figure 3 The process of the improved genetic algorithm |
为保证最短路算法在路径问题分析中的现实随机波动性及有效性,按照主干线永久道路、半干线、采排场临时道路、折返路段4个道路级别对某矿实际道路网络进行分类,并考虑矿山行车安全,参考文献[1, 31]给出各类型路段行车速度上限,以及路段阻力折算系数[31],如表 1所示。为进一步验证文中算法在运输模型中现实优化效果,笔者分别采用Dijkstra算法与文献[7-8]中提出的粒子群算法参与对比,并采用路段时变行车速度上限指标计算对应的时变运输功。
| 表 1 路段行车速度上限及阻力系数折算表 Table 1 The speed limit and the drag coefficient of the road traffic |
算法实验采用C#.Net编译并进行了一系列的仿真测试,实验平台及参数如下:
① 普通PC,CPU:I5 2.9GHz,RAM:8G,Windows 7 X64 Edition;
② 遗传算法实验参数:算法种群大小Popsize=50;最大进化代数GMax=250;交叉概率pc=0.8,变异概率pm=0.05;
③ 时变运输功计算参数:实例运输卡车[32]采用MT5500B,空车自重223 t,额定载重326 t,最大载重360 t,平装容积158 m3,2:1堆装218 m3;参考文献[14]中计算方法给出良好路面条件下载重卡车滚动阻力系数f=c·fz=1.3×(0.0 066+0.0 000 286·v)计算,其中c表示路况条件系数,无量纲;fz表示良好路面下滚动阻力系数,无量纲;v表示车辆行驶的速度上限。在实际路面条件下需要对阻力系数进一步换算,按照具体的道路类型换算系数如表 1示;坡度阻力取r=sin α=0.08;挡风面积A=52.48 m2,风阻系数C=2.4,松散土体容重1.68 t/m3。
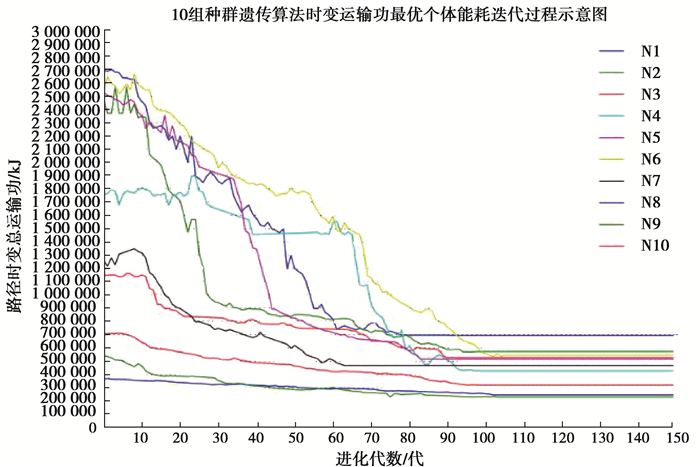
3.2 实验结果分析为直观表现10组测试实例的能耗变化,图 4给出各代种群最优个体的能耗值迭代过程,从中可以看出改进GA算法迭代过程中,解均收敛于物料时变运输功的最小值,在实际路径寻优过程中均能获得能耗最低的优化路径解,说明该算法具有较好收敛性,可快速收敛于全局最优解。
|
图 4 时变运输功最优个体能耗迭代过程 Figure 4 The iterative process of energy consumption for the optimal individual energy consumption |
为进一步揭示文中算法的能耗优势,分别对Dijkstra和PSO算法优化的路径结果进行全局时变总运输功统计,并从运距、优化效果和时间性能3方面对10组测试实例的优化参数进行了对比,如表 2所示,表中等效运距、运输功最优解以及时间效率均加下划线表示。文中利用先验条件过滤了10组测试实例的非关联节点,并在表中统计了关联节点数。从表 2中对比数据可以发现,一方面两类算法均能计算得到最优解,但Dijkstra和PSO算法更加关注静态网络中路径节点间距离总和最小,并能够得到较为理想且相同的等效运距全局最优解;而文中改进的GA算法则着眼于动态变权重网络中目标路径运输功总和最低,能得到较为理想的运输功最优解。另一方面,节点间等效运输距离和最短的路径其运输功并不最小,在相同路面条件下产生该现象的原因在于:①当卡车遇到频繁折返时,其阻力较之直线行驶时是成倍递增的,会大幅度增加卡车运输功;②当卡车在频繁克服高程爬坡时,由于坡度阻力的增加也会导致总体阻力做功变化;③道路阻力系数是一个随速度小幅度波动的变量,但以数百吨卡车重量为基数的阻力计算会放大上述波动,对优化结果会造成较大影响。
| 表 2 改进算法优化参数对比 Table 2 Improved algorithm optimization parameter comparison |
为进一步说明算法效率,通过对表 2中对执行效率对比统计可知,GA以及PSO算法均能较快的收敛于目标最优解,除实例N3外其余各组中改进GA算法收敛速度均优于前2种算法,由上述分析可知文中算法能低能耗且快速的收敛于路径问题的全局最优解。
4 结论1) 通过实验对比可知,采用时变运输功计算路径优化问题有助于获得路径能耗的全局最优解,而非物理距离最短路,能有效的解决运输系统能耗问题,控制矿山运输成本,提高矿山整体经济效益;
2) 对于路网间的时变运输计算是一个典型的NP难问题,通过引入基于随机过程概率优化模型有益于进一步简化问题求解,保证原始问题快速获得最优解;
3) 采用启发式初始化种群、精英选择结合轮盘赌的选择策略能较大幅度的提升遗传算法收敛速度,对于提高时变运输功决策计算性能具有积极的作用,能进一步提高算法执行效率。
| [1] |
白润才, 马云东, 李建刚. 露天矿卡车实时调度机安全保证预警理论与应用研究[M]. 沈阳: 沈阳大学出版社, 2005: 31-33.
BAI Runcai, MA Yundong, LI Jiangang. Research of theory on truck real-time dispatch and safety assurance pre-warning system in surface mine and it's application[M]. Shenyang: Shenyang University Press, 2005: 31-33. (in Chinese) |
| [2] |
魏强, 李克民, 姚绍武.
露天矿物料流规系统的设计与实现[J]. 中国矿业大学学报, 2003, 32(2): 180–182.
WEI Qiang, LI Kemin, YAO Zhaowu. Design and realization of surface ming materiel-stream programming system[J]. Journal of China University of Mining & Technology, 2003, 32(2): 180–182. (in Chinese) |
| [3] |
张幼蒂, 王玉浚. 矿业系统工程[M]. 徐州: 中国矿业大学出版社, 2000: 292-297.
ZHANG Youdi, WANG Yujun. Mining systems engineering[M]. Xuzhou: China Mining University Press, 2000: 292-297. (in Chinese) |
| [4] | Choi Y, Park H D, Sunwoo C, et al. Multi-criteria evaluation and least-cost path analysis for optimal haulage routing of dump trucks in large scale open-pit mines[J]. International Journal of Geographical Information Science, 2009, 23(12): 1541–1567. DOI:10.1080/13658810802385245 |
| [5] |
刘艳章, 冯毓松.
运输功的计算及其在优选排土场方案中的应用[J]. 化工矿物与加工, 2003, 24(12): 24–27.
LIU Yanzhang, FENG Yusong. The calculation of the transportation work and its application in the optimization scheme[J]. Industrial Minerals and Processing, 2003, 24(12): 24–27. DOI:10.3969/j.issn.1008-7524.2003.12.009 (in Chinese) |
| [6] |
白润才, 刘闯, 刘光伟, 等.
季节性剥离露天煤矿内排开拓运输系统优化[J]. 重庆大学学报, 2014, 37(8): 99–104.
BAI Runcai, LIU Chuang, LIU Guangwei, et al. Optimization of in-pit haulage system development during internal dumping in seasonal stripping surface coal mine[J]. Journal of Chongqing University, 2014, 37(8): 99–104. DOI:10.11835/j.issn.1000-582X.2014.08.014 (in Chinese) |
| [7] |
李勇, 胡乃联, 李国清.
基于改进粒子群算法的露天矿运输调度优化[J]. 中国矿业, 2013, 22(4): 98–105.
LI Yong, HU Nailian, LI Guoqing. Open-pit hauling dispatching optimization based on improved PSO algorithm[J]. China's Mining Industry, 2013, 22(4): 98–105. (in Chinese) |
| [8] |
陈应显, 韩明峰.
改进粒子群算法的露天矿路径优化研究[J]. 微电子学与计算机, 2011, 28(11): 61–68.
CHEN Yingxian, HAN Mingfeng. Improved particle swarm optimization on open-pit vehicle routing problem[J]. Microelectronics & Computer, 2011, 28(11): 61–68. (in Chinese) |
| [9] |
孙臣良, 刘静.
露天矿运输道路网络的建立及其路径优化[J]. 科技导报, 2011, 29(30): 47–51.
SUN Chenliang, LIU Jing. Establishing of surface mine road networks and optimization of their transportation route[J]. Science and Technology Review, 2011, 29(30): 47–51. DOI:10.3981/j.issn.1000-7857.2011.30.006 (in Chinese) |
| [10] | Sattarvand J. Long-term open-pit planning by ant colony optimization[D]. Iran: RWTH Aachen University, 2009. http://www.researchgate.net/publication/27560837_Long-term_open-pit_planning_by_ant_colony_optimization |
| [11] |
雷芬. 随机网络中的动态最短路研究[D]. 北京: 中央民族大学, 2009. LEI Fen. The most short-circuit research in the random network[D]. Beijing: Minzu University of China, 2009. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10052-2009193629.htm |
| [12] |
董振宁, 张召生.
随机网络的最短路问题[J]. 山东大学学报, 2003, 38(3): 6–9.
DONG Zhenning, ZHANG Zhaosheng. The most short-circuit problem of a random network[J]. Journal of Shandong University, 2003, 38(3): 6–9. (in Chinese) |
| [13] | Miller-Hooks E D, Mahassanic H S. Least possible time paths in stochastic, time-varying networks[J]. Compute & Operations Research, 1998, 25(12): 27–54. |
| [14] |
余志生. 汽车理论[M]. 第三版. 北京: 机械工业出版社, 2000: 19-29.
YU Zhisheng. Automobile theory[M]. 3rd edition. Beijing: Mechanical Industry Press,, 2000: 19-29. (in Chinese) |
| [15] |
王小平, 曹立明. 遗传算法:理论、应用与软件实现[M]. 西安: 西安交通大学出版社, 2002: 18-50.
WANG Xiaoping, CAO Liming. Genetic algorithm:theory, application and software implementation[M]. Xi'an: Xi'an Jiaotong University Press, 2002: 18-50. (in Chinese) |
| [16] | Chu P C, Beasley J E. A genetic algorithm for the generalised assignment problem[J]. Computers & Operations Research, 1997, 24(1): 17–23. |
| [17] | Osman I H. Heuristics for the generalised assignment problem:simulated annealing and tabu search approaches[J]. OR Spektrum, 1995, 17(4): 211–225. DOI:10.1007/BF01720977 |
| [18] | Amini M M, Racer M. A rigorous computational comparison of alternative solution methods for the generalized assignment problem[J]. Management Science, 1994, 40(7): 868–890. DOI:10.1287/mnsc.40.7.868 |
| [19] | Klastorin T D. An effective subgradient algorithm for the generalized assignment problem[J]. Computers & Operations Research, 1979, 6(3): 155–164. |
| [20] |
岳嵚, 冯珊.
遗传算法的计算性能的统计分析[J]. 计算机学报, 2009, 32(12): 2389–2392.
YUE Qin, FENG Shan. The statistical analyses for computational performance of the genetic algorithms[J]. Chinese Journal of Computers, 2009, 32(12): 2389–2392. (in Chinese) |
| [21] | Ehrlich P R, Raven P H. Butterflies and plants:a study in coevolution[J]. Evolution, 1964, 18(4): 586–608. DOI:10.1111/evo.1964.18.issue-4 |
| [22] | Li Q H, Yang S D, Ruan Y L. Imporving optimization for genetic algorithums based on level set[J]. Journal of Computer Research and Development, 2006, 43(9): 1624–1629. DOI:10.1360/crad20060920 |
| [23] | Liang J J, Suganthan P N, Deb K. Novel composition test functions for numerical global optimization[C]//Swarm Intelligence Symposium, 2005. SIS 2005. Proceedings 2005 IEEE. June 8-10, 2005. [S. l. ]: IEEE, 2005: 68-75. https://www.researchgate.net/publication/4170894_Novel_composition_test_functions_for_numerical_global_optimization |
| [24] | Holland J H. Adaptation in natural and artificial systems[M]. MA, USA: MIT Press, 1992. |
| [25] | Ecemis I, Bonabeau E, Ashburn T. Interactive estimation of agent-based financial markets models: modularity and learning[C]//GECCO 2005 Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, Washington DC, USA, June 25-29, 2005. New York, USA: ACM, 2005: 1897-1904. http://dl.acm.org/citation.cfm?id=1068330 |
| [26] | Biles J, Anderson P, Loggi L. Neural network fitness functions for a musical IGA[C/OL]//International ICSC Symposium on Intelligent Industrial Automation and Soft Computing(1996). [S. l. ]: RIT, 1996: 39-44. |
| [27] | Solomon C J, Gibson S J, Mist J J. Interactive evolutionary generation of facial composites for locating suspects in criminal investigations[J]. Applied Soft Computing, 2013, 13(7): 3298–3306. DOI:10.1016/j.asoc.2013.02.010 |
| [28] |
杨卫波, 王万良, 张景玲, 等.
基于遗传模拟退火算法的矩形件优化排样[J]. 计算机工程与应用, 2016, 52(7): 259–263.
YANG Weibo, WANG Wanliang, ZHANG Jingling, et al. Packing optimization of rectangles based on improved genetic anneling algorithm[J]. Computer Engineering and Application, 2016, 52(7): 259–263. (in Chinese) |
| [29] |
张水舰, 刘学军, 杨洋.
动态随机最短路径算法研究[J]. 物理学报, 2016, 52(7): 259–263.
ZHANG Shuijian, LIU Xuejun, YANG Yang. Dynamic stochastic shortest path algorithm[J]. Acta Physica Sinica, 2016, 52(7): 259–263. (in Chinese) |
| [30] |
盛骤, 谢式千, 潘承毅, 等. 概率论与数理统计[M]. 第四版. 北京: 高等教育出版社, 2008: 72-76.
SHENG Zhou, XIE Shiqian, PAN Chenyi, et al. Probability and mathematical statistics[M]. 4th edition. Beijing: Higher Education Press, 2008: 72-76. (in Chinese) |
| [31] |
于润沧. 采矿工程师手册(上)[M]. 北京: 冶金工业出版社, 2009: 261-283.
YU Runcang. The mining engineer's handbook[M]. Beijing: Metallurgical Industry Press, 2009: 261-283. (in Chinese) |
| [32] |
哈尔乌素露天矿生产技术科. 哈尔乌素露天煤矿设备技术手册[Z]. 鄂尔多斯: 哈尔乌素露天矿, 2009. HaErWaSu Production and Technigue Section. HaErWuSu open-pit coal mine equipment technical manual[Z]. Erdos: HaErWuSu Open-pit, 2009. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41

