在现代工业、电子产品和新能源发电等领域,DC-DC变换器发挥着越来越重要的作用。选择变换器时优先考虑效率高、成本低和结构简单的变换器[1-2]。相较于其他隔离式变换器,Buck变换器因其结构简单等优点而被广泛使用。传统的Buck变换器采用肖特基二极管作为整流管,其正向导通压降最低可达0.3 V。随着微处理器技术的快速发展[3],以及移动电子产品对小体积和长电池寿命的需求[4],需要Buck变换器工作在低压大电流的工作条件下。然而在这种工作条件下,肖特基二极管的压降会严重降低Buck变换器的效率,因此, 人们将同步整流技术与Buck变换器相结合,使用低导通电阻的MOSFET作为整流管,代替肖特基二极管,从而提高Buck变换器的效率。
按建模的方式进行分类,DC-DC变换器的控制方法分为线性控制和非线性控制。传统DC-DC变换器的控制方法采用线性控制,基于小信号模型,在稳态点对DC-DC变换器进行线性化处理并设计控制器[5-6]。由于开关变换器本身就是强非线性系统,传统的小信号处理结合线性控制理论的方法存在较大的局限性[7]。非线性控制能使开关变换器对电路参数变化和输入、负载扰动具有很好的鲁棒性和动态响应[8]。在各种非线性控制中,滑模控制易于实现,对参数变化不敏感[9-10],对外部扰动鲁棒性强,动态响应速度快,同时考虑大信号和小信号。传统的直接一阶滑模控制,采用滞环的方式实现,文献[11]针对Buck变换器采用滞环方式实现了直接滑模控制,文献[12]针对Buck变换器采用滞环方式设计了全局滑模控制器。一阶滑模控制需要同时检测输出电压和电容电流并且存在抖振问题,而二阶滑模可以消除一阶滑模中普遍存在的抖振问题[13],并比一阶滑模具有更高的精度。大多数二阶滑模控制算法需要知道滑模量的一阶导数或其正负号[14],常见的二阶滑模算法有:螺旋算法、超螺旋算法、次优算法和给定收敛律算法[15]。文献[16]和文献[17]分别针对Buck-Boost变换器和Buck变换器使用超螺旋算法设计了二阶滑模控制器,文献[18]和文献[19]针对Buck变换器和同步Buck变换器使用改进次优算法设计了二阶滑模控制器,体现出二阶滑模控制的优越性。
文中采用改进的次优算法[18-19],针对同步整流Buck变换器,只需要检测输出电压,不需要使用电流互感器检测电容电流,通过构建状态机来实现二阶滑模控制。通过采用滞环改进的次优算法,使得变换器输出电压达到稳态值时的开关频率为可控有限值。该方法既保留了滑模控制的鲁棒性,提高控制精度,还减少传感器的使用,简化了电路结构。
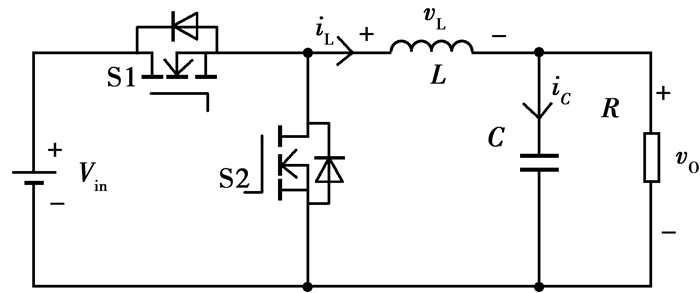
1 同步Buck变换器建模同步Buck变换器电路如图 1所示。Vin为输入电压,vo为输出电压,S1为主开关管,S2为同步整流管,C为电容,iC为电容电流,L为电感,iL为电感电流,vL为电感电压,R为负载电阻。
|
图 1 同步Buck变换器电路 Figure 1 Circuit of synchronous buck converter |
令同步Buck变换器工作于CCM模式,此时具有如下2种工作状态:
1) 当开关变换器处于主开关管S1导通,同步管S2关断时,电感电流增加,此时,根据基尔霍夫定律有
| $ \left\{ {\begin{array}{*{20}{c}} {{v_{\rm{L}}} = L{{\dot i}_{\rm{L}}} = {V_{{\rm{in}}}} - {v_{\rm{o}}},}\\ {{i_{\rm{L}}} = C{{\dot v}_{\rm{o}}} + \frac{{{v_{\rm{o}}}}}{R}。} \end{array}} \right. $ | (1) |
2) 当开关变换器处于主开关管S1关断,同步管S2导通时,电感电流下降,此时,根据基尔霍夫定律有
| $ \left\{ \begin{array}{l} {v_{\rm{L}}} = L{{\dot i}_{\rm{L}}} = - {v_{\rm{o}}},\\ {i_{\rm{L}}} = C{{\dot v}_{\rm{o}}} + \frac{{{v_{\rm{o}}}}}{R}。\end{array} \right. $ | (2) |
对2种工作状态下得到的式(1)和式(2)进行整理,引入控制变量u={0, 1},得到同步Buck变换器在非连续控制时的状态空间模型
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot i}_{\rm{L}}}}\\ {{{\dot v}_{\rm{o}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{L}}\\ {\frac{1}{C}}&{ - \frac{1}{{RC}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_{\rm{L}}}}\\ {{v_{\rm{o}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\frac{{{V_{{\rm{in}}}}}}{L}}\\ 0 \end{array}} \right]u。$ | (3) |
二阶滑模是一阶滑模的扩展,二阶滑模不但保留了一阶滑模控制的鲁棒性,还能有效消除一阶滑模控制存在的抖振现象。对于式(3),设滑模变量s为
| $ s = e = {V_{{\rm{ref}}}} - {v_{\rm{o}}}, $ | (4) |
式中,e为电压偏差,Vref为参考电压。根据式(3)和式(4),求出滑模变量s的一阶导和二阶导
| $ \dot s = \frac{{{v_{\rm{o}}}}}{{RC}} - \frac{{{i_{\rm{L}}}}}{C}, $ | (5) |
| $ {\rm{\ddot s}} = \left( {\frac{1}{{LC}} - \frac{1}{{{{\left( {RC} \right)}_2}}}} \right){v_{\rm{o}}} + \frac{1}{{R{C^2}}}{i_{\rm{L}}} - \frac{{{V_{{\rm{in}}}}}}{{LC}}u。$ | (6) |
整理式(4)~式(6)得
| $ {\rm{\ddot s}} + \frac{1}{{RC}}\dot s + \frac{1}{{LC}}s = \frac{1}{{LC}}\left( {{V_{{\rm{ref}}}} - u \cdot {V_{{\rm{in}}}}} \right)。$ | (7) |
传统一阶滑模控制滑模变量为
次优算法由时间最优的Bang-Bang控制发展而来[21],定义其控制律为[22]
| $ \left\{ \begin{array}{l} u\left( t \right) = - \alpha \left( t \right) \cdot U{\rm{sign}}\left( {s - \beta \cdot {s_{{\rm{SP}}}}} \right),\\ \alpha \left( t \right) = \left\{ \begin{array}{l} 1,{\rm{if}}\left( {s - \beta \cdot {s_{{\rm{SP}}}}} \right) \cdot {s_{{\rm{SP}}}} \ge 0,\\ {\alpha ^ * },{\rm{if}}\left( {s - \beta \cdot {s_{{\rm{SP}}}}} \right) \cdot {s_{{\rm{SP}}}} < 0, \end{array} \right.\\ \beta \in \left[ {0,1} \right)。\end{array} \right. $ | (8) |
式中:U为峰值系数; α为调制系数; β为期望系数; sSP为上一次
| $ \left\{ \begin{array}{l} u\left( t \right) = \alpha \left( t \right){\rm{sign}}\left( {s - \beta \cdot {s_{{\rm{SP}}}}} \right),\\ \alpha \left( t \right) = \left\{ \begin{array}{l} 1,{\rm{if}}\left( {s - \beta \cdot {s_{{\rm{SP}}}}} \right) \cdot {s_{{\rm{SP}}}} \ge 0,\\ 0,{\rm{if}}\left( {s - \beta \cdot {s_{{\rm{SP}}}}} \right) \cdot {s_{{\rm{SP}}}} < 0, \end{array} \right.\\ \beta \in \left[ {0,1} \right)。\end{array} \right. $ | (9) |
对于二阶滑模而言,式中sSP即为系统上一次求得的奇点。由于β介于0和1之间,每一次的切换点距原点距离均小于上一次求得的奇点距原点的距离。
采用式(9)的控制律进行控制时,需要获得

|
图 2 基于次优算法的二阶滑模相轨迹 Figure 2 Phase trajectory of two order sliding mode control based on suboptimal algorithm |
当系统达到稳态时,该算法会造成开关频率趋近于无穷大,这对同步Buck变换器来说难以实现。因此,引入滞环来限制系统稳定时的开关频率。此时,二阶滑模控制律为
| $ u\left( t \right) = \left\{ \begin{array}{l} {\rm{sign}}\left( {s - \beta \cdot {s_{{\rm{SP}}}} - {\Delta _{{\rm{ON}}}}} \right),s < 0,\mu = - 1,\\ {\rm{sign}}\left( {s - {s_{{\rm{SP}}}} - {\Delta _{{\rm{OFF}}}}} \right),s < 0,\mu = 1,\\ {\rm{sign}}\left( {s - \beta \cdot {s_{{\rm{SP}}}} - {\Delta _{{\rm{OFF}}}}} \right),s > 0,\mu = 1,\\ {\rm{sign}}\left( {s - {s_{{\rm{SP}}}} - {\Delta _{{\rm{ON}}}}} \right),s > 0,\mu = - 1。\end{array} \right. $ | (10) |
式中:sSP为系统上一次求得的奇点,随系统状态变化而改变,需要被系统保存;ΔON为导通滞环环宽,ΔOFF为关断滞环环宽。
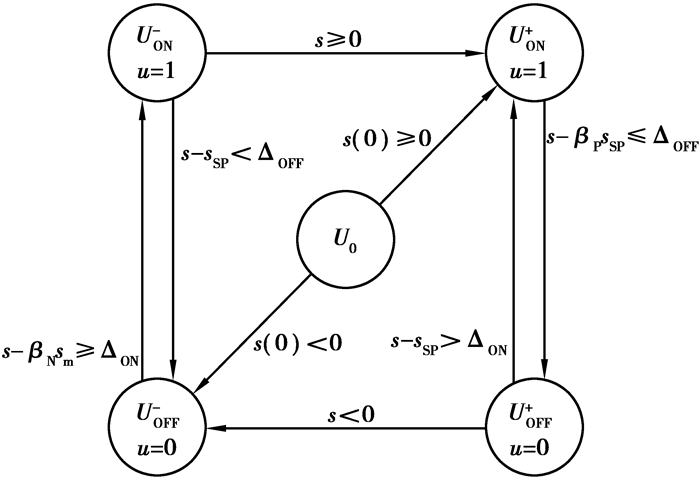
现做如下定义[19, 23]:s>0且
|
图 3 二阶滑模控制器状态机框图 Figure 3 State-machine block diagram of two order sliding mode controller |
下面对期望系数进行计算,对于式(7),整理得
| $ \int {LC\dot s{\rm{d}}\dot s} = \int {\left[ {\left( {u{V_{{\rm{in}}}} - {V_{{\rm{ref}}}}} \right) - s - \frac{L}{R}\dot s} \right]{\rm{d}}s} , $ | (11) |
对于式(11)中,
| $ \int {\frac{L}{R}\dot s{\rm{d}}\dot s} = \int {\frac{L}{R}{i_c}{\rm{d}}\left( {{v_{\rm{o}}} - {V_{{\rm{ref}}}}} \right)} = \frac{L}{R}\int {i_c^2{\rm{d}}t} 。$ | (12) |
对于同步Buck变换器,电容电流iC幅值很小,并且电感L以微亨(μH)为单位,因此认为该项近似为0。滞环的目的是在系统达到稳态时限制开关频率且动态时环宽要远小于滑模变量的值,因此在进行分析时,认为Δ≈0。令
| $ \int {{{\dot s}_c}{\rm{d}}{{\dot s}_c}} = \int {\left[ {\left( {{V_{{\rm{ref}}}} - u{V_{{\rm{in}}}}} \right) - s} \right]{\rm{d}}s} 。$ | (13) |
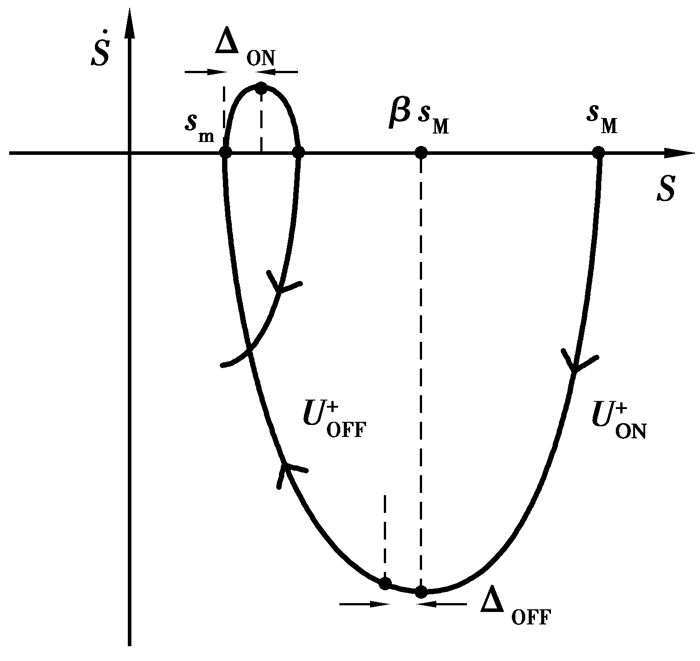
当s>0时,系统相轨迹如图 4所示。
|
图 4 s>0时系统相轨迹 Figure 4 Phase trajectory of system when s > 0 |
以(sM, 0)为初值,得到当u(t)=UON+=1时的相轨迹方程为
| $ {\left[ {s + \left( {{V_{{\rm{in}}}} - {V_{{\rm{ref}}}}} \right)} \right]^2} + \dot s_c^2 = {\left[ {{s_{\rm{M}}} + \left( {{V_{{\rm{in}}}} - {V_{{\rm{ref}}}}} \right)} \right]^2}, $ | (14) |
设切换点坐标为(βsM,
| $ {\left[ {\beta {s_{\rm{M}}} + \left( {{V_{{\rm{in}}}} - {V_{{\rm{ref}}}}} \right)} \right]^2} + \dot s_{\min }^2 = {\left( {{s_{\rm{M}}} + {V_{{\rm{ref}}}}} \right)^2}。$ | (15) |
以(βsM,
| $ {\left( {s - {V_{{\rm{ref}}}}} \right)^2} + \dot s_c^2 = {\left( {{V_{{\rm{ref}}}} - \beta {s_{\rm{M}}}} \right)^2} + \dot s_{\min }^2, $ | (16) |
此时,相轨迹经过(sm, 0),代入式(16)得
| $ {\left( {{s_{\rm{m}}} - {V_{{\rm{ref}}}}} \right)^2} = {\left( {{V_{{\rm{ref}}}} - \beta {s_{\rm{M}}}} \right)^2} + \dot s_{\min }^2。$ | (17) |
联立式(15)和式(17)得到
| $ \beta = \frac{{s_{\rm{M}}^2 + 2\left( {{V_{{\rm{in}}}} - {V_{{\rm{ref}}}}} \right) \cdot {s_{\rm{M}}} + \left( {2{V_{{\rm{ref}}}} - {s_{\rm{m}}}} \right) \cdot {s_{\rm{m}}}}}{{2{V_{{\rm{in}}}}}}。$ | (18) |
为保证系统响应无超调[19],β取值应保证系统相轨迹不穿越纵轴,sm满足:0≤sm<sM≤Vref。此种情况下,当sm=0时β取最小值,为
| $ {\beta _{\rm{P}}} \ge \frac{{{s_{\rm{M}}} + 2\left( {{V_{{\rm{in}}}} - {V_{{\rm{ref}}}}} \right)}}{{2{V_{{\rm{in}}}}}}。$ | (19) |
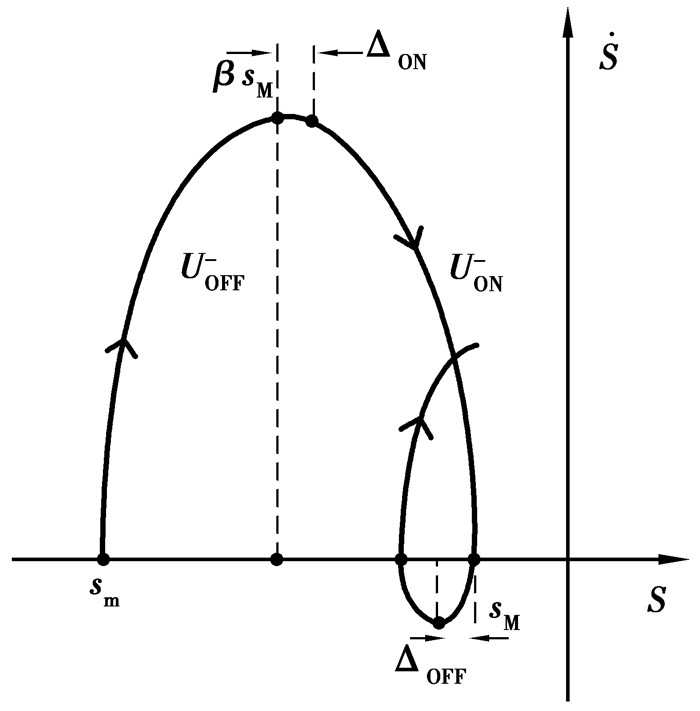
当s<0时,相轨迹如图 5所示。
|
图 5 s<0系统相轨迹 Figure 5 Phase trajectory of system when s < 0 |
同理,在此种情况下,当sM=0时β取最小值,为
| $ {\beta _{\rm{N}}} \ge \frac{{2{V_{{\rm{ref}}}} - {s_{\rm{m}}}}}{{2{V_{{\rm{in}}}}}}。$ | (20) |
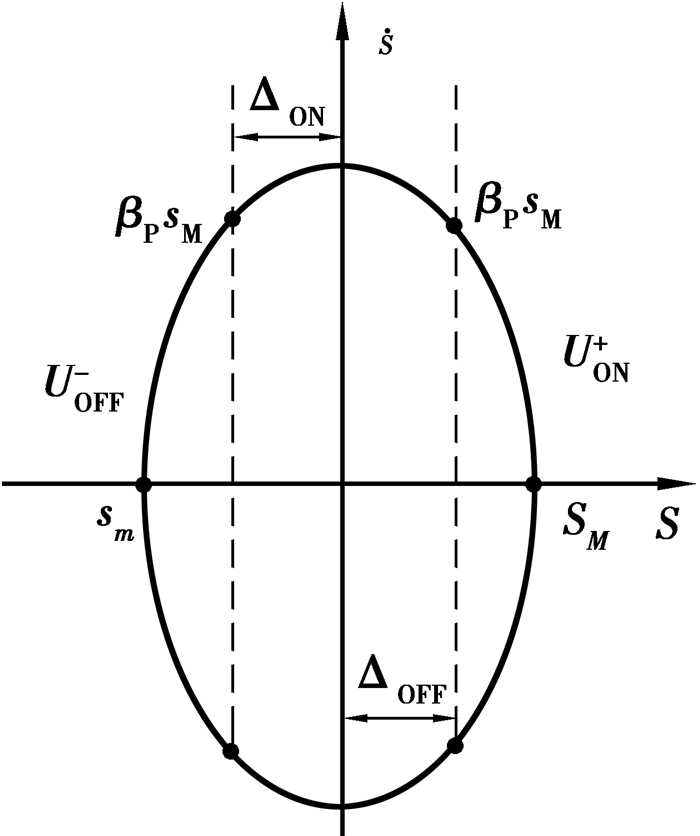
在2种情况下,令β取最小值,此时系统的响应最快。当系统达到稳态时,滞环的作用会变得明显,会使系统在原点附近形成稳定的极限环,如图 6所示。
|
图 6 系统稳定形成极限环 Figure 6 Stable limit cycle of system |
对于同步Buck变换器来说,此极限环不会影响系统性能,极限环的幅值对应于变换器输出电压的纹波值。如果认为系统形成稳定极限环时,在纵轴上进行状态切换[19],则满足
| $ \left\{ \begin{array}{l} {\beta _{\rm{N}}}{s_{\rm{m}}} + {\Delta _{{\rm{ON}}}} = 0,\\ {\beta _{\rm{P}}}{s_{\rm{M}}} - {\Delta _{{\rm{OFF}}}} = 0。\end{array} \right. $ | (21) |
当输出电压达到稳态时,|sm|和|sM|对应了电压纹波相对输出电压平均值的峰值和谷值,存在|sm|≪2Vin,|sM|≪2Vin,此时βN与βP中的sm和sM项可以忽略,根据式(4)及Buck变换器纹波电压与开关周期的关系,可以得到
| $ {s_{\rm{M}}} = \frac{1}{C}\int_0^{DT/2} {{i_c}{\rm{d}}t} = \frac{{{V_{{\rm{in}}}} - {V_{\rm{o}}}}}{{8LC}} \cdot {D^2}{T^2}, $ | (22) |
式中:Vo为变换器稳定时输出电压的平均值,等于Vref;T为开关周期; D为占空比,为Vo与Vin的比值。联立式(21)和式(22),求得关断滞环环宽为
| $ {\Delta _{{\rm{OFF}}}} = \frac{{{V_{{\rm{in}}}} \cdot {D^2} \cdot {{\left( {1 - D} \right)}^2} \cdot {T^2}}}{{8LC}}, $ | (23) |
同理,可以求得导通滞环环宽为
| $ {\Delta _{{\rm{ON}}}} = \frac{{{V_{{\rm{ref}}}} \cdot D \cdot {{\left( {1 - D} \right)}^2} \cdot {T^2}}}{{8LC}}, $ | (24) |
可以发现,ΔON=ΔOFF。定义滞环环宽
| $ \Delta = {\Delta _{{\rm{ON}}}} - {\Delta _{{\rm{OFF}}}}, $ | (25) |
联立式(23)~式(25),得到同步Buck变换器工作于稳定状态时的开关频率
| $ {f_{\rm{s}}} = \frac{{{V_{{\rm{ref}}}}\left( {{V_{{\rm{in}}}} - {V_{{\rm{ref}}}}} \right)}}{{2{V_{{\rm{in}}}}\sqrt {LC{V_{{\rm{in}}}}\Delta } }}。$ | (26) |
由式(26)可知,稳定工作状态下,引入滞环可以有效控制开关的开关频率。
3 仿真验证与结果分析为验证算法的可行性和控制性能,在Matlab/Simulink环境下针对同步Buck变换器,分别搭建直接一阶滑模和二阶滑模控制器,二者均通过状态机实现。同步Buck变换器的参数为:L=120 μH,C=260 μF,输入电压Vin=3.3~12 V,正常工作情况下为5 V,期望输出电压Vref=1.8 V,负载R=0.09~1 Ω,正常工作负载电阻为0.18 Ω,开关频率fS=100 kHz,变换器工作于CCM模式。仿真算法选择VariableStepDiscrete,仿真时间为0.01 s。一阶滑模滑动系数按正常工作的负载电阻进行选取,取为
变换器在启动过程中,滑模变量s的初始值s(0)=Vref,此时滑模变量的初值为系统奇点的最大值sM。根据公式(19)计算初始的期望系数βP,得到在不同负载时变换器的输出电压、启动阶段相轨迹以及稳定状态时的相轨迹如图 7~图 9所示,以及变换器在不同负载时的输出电压数据如表 1所示。
|
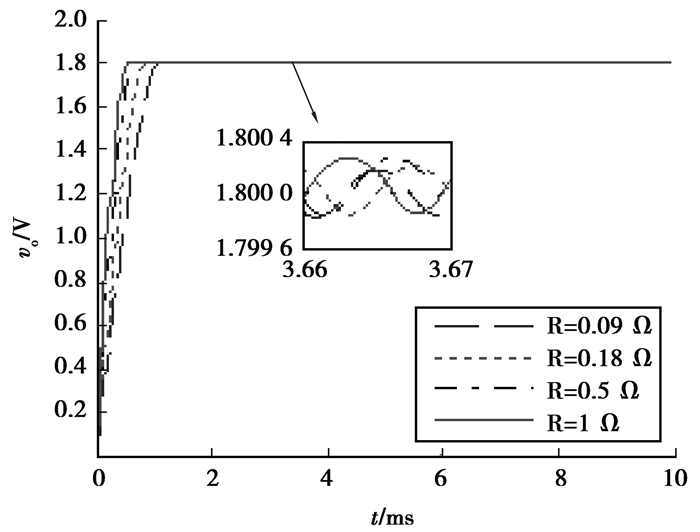
图 7 不同负载条件下变换器输出电压波形 Figure 7 Waveform of output voltage converter under different load conditions |
|
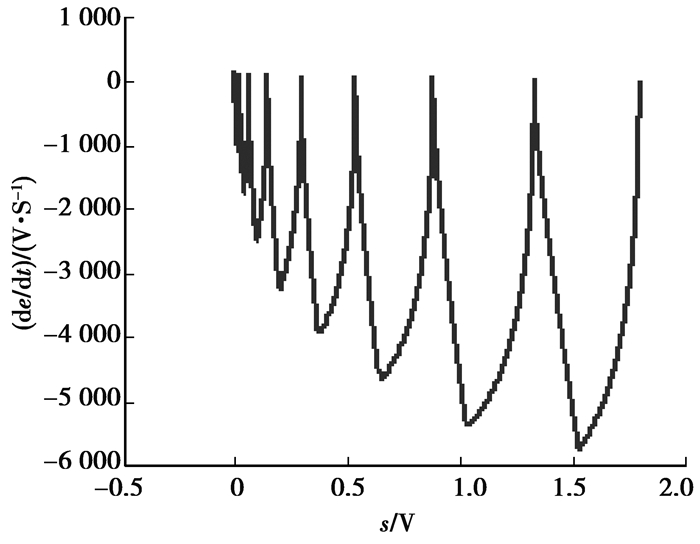
图 8 二阶滑模控制下变换器相轨迹 Figure 8 Phase trajectory of second order sliding mode control |
|
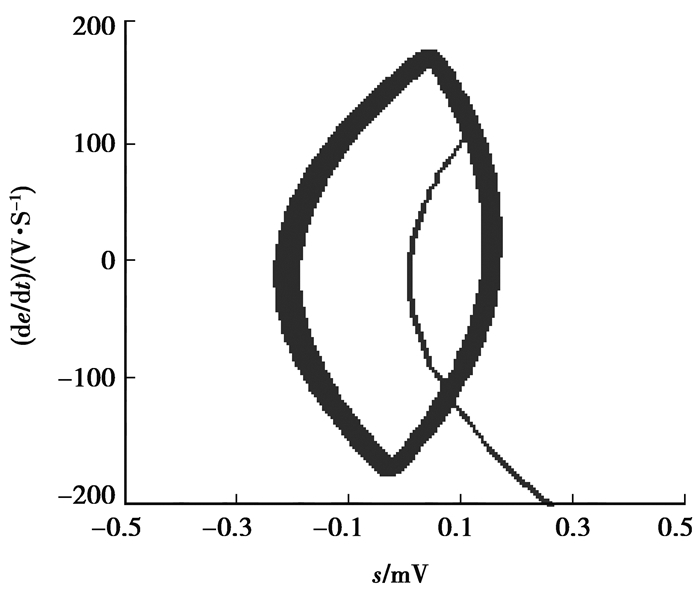
图 9 系统稳定时形成的极限环 Figure 9 Limit cycles of the system stability |
| 表 1 不同负载时变换器输出电压 Table 1 Value of ouput valtage under different load conditions |
从图 7可以看到,根据式(19)和式(20)计算得到的期望系数可以使二阶滑模控制器在任何负载情况下对同步Buck变换器的控制均能保证输出电压无超调。表 1表明,负载会影响二阶滑模同步Buck变换器的启动时间,负载越小(负载电阻越大),启动时间越短;在启动过程中,出现了主开关管关断的情况,这是次优算法特性引起的,虽然会延迟启动时间,但可以保证二阶滑模控制器在任何负载情况下均能做到输出无超调,若想缩短启动时间,可以在系统初始化时,手动调节初始的期望系数,以实现启动时间最短。负载越大,输出电压稳态误差越小,输出电压稳态误差近似为0,输出电压纹波随负载变化有微小变化,负载越大,纹波电压越小。由于在前面的分析中未考虑输出电容的ESR,开关管的导通电阻和滤波电感的ESR,因此, 仿真结果与理论分析略有不同。输出电容ESR的存在导致了极限环的偏移,并使开关频率低于理论值;而开关管的导通和滤波电感的ESR导致开关频率会随负载改变而发生变化。
3.2 启动特性与稳态特性测试在负载电阻为0.18 Ω,输出电流为10 A时对一阶滑模和二阶滑模启动特性进行比较,对二阶滑模初始期望系数进行了手动设置,得到电压波形如图 10所示, 一阶滑模与二阶滑模控制下正常工作负载工作时的测试结果如表 2所示。

|
图 10 一阶滑模与二阶滑模控制变换器输出电压波形 Figure 10 Waveform of converter output voltage under first-order and second-order sliding mode control |
| 表 2 正常工作负载时测试结果 Table 2 Test result under normal load |
从图 10和表 2可以看到,一阶滑模和二阶滑模均能实现输出电压无超调。在相同负载时,经过手动设置期望系数的二阶滑模在0.35 ms时达到稳态,一阶滑模则在0.6 ms时达到稳态,二阶滑模的动态响应比一阶滑模快,二阶滑模保留了滑模控制的快速无超调的特点;二阶滑模控制下变换器的电压稳态误差小于一阶滑模控制。由于二阶滑模控制的开关频率高于一阶滑模控制,故二阶滑模控制的纹波电压小于一阶滑模控制。
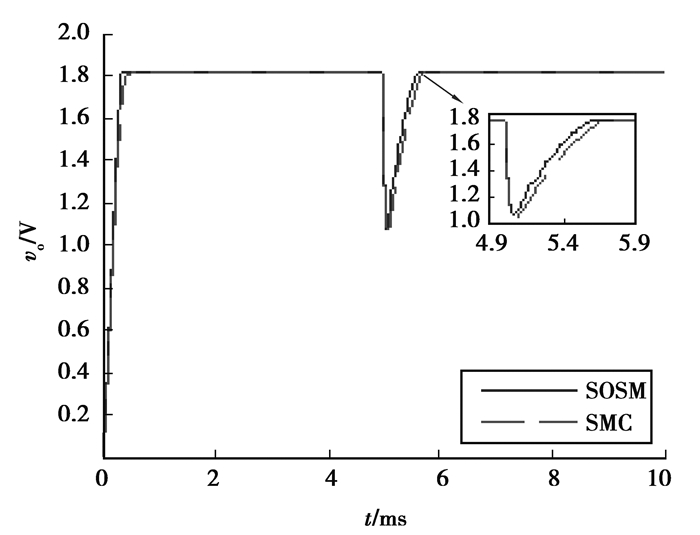
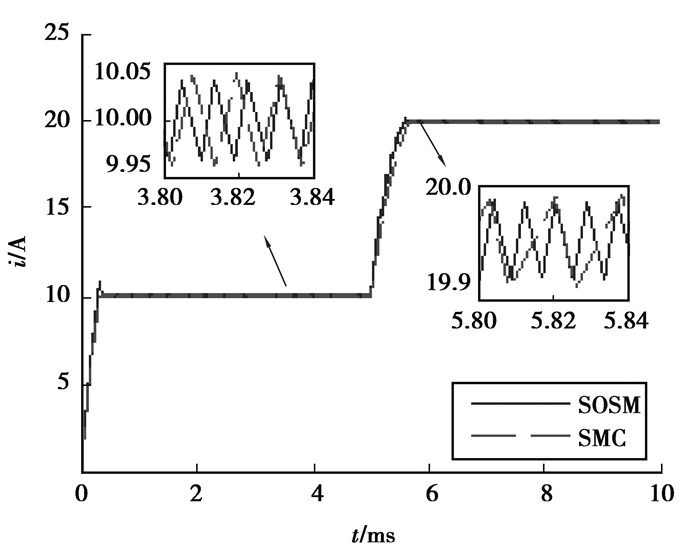
3.3 负载扰动测试令负载电阻在0.005 s时从0.18 Ω变化到0.09 Ω,输出电流从10 A变化到20 A,对比一阶滑模和二阶滑模对负载扰动的鲁棒性,电压电流波形和测试结果如图 11、图 12和表 3所示。
|
图 11 负载扰动实验输出电压波形 Figure 11 Waveform of output voltage under load disturbance experiment |
|
图 12 负载扰动实验电感电流波形 Figure 12 Waveform of inductor current under load disturbance experiment |
| 表 3 负载扰动测试结果(ΔI=10 A) Table 3 Test result under load disturbance experiment |
从图中可以看到,负载发生10 A的大扰动时,一阶滑模和二阶滑模均使输出电压迅速且无超调恢复到稳态值,表现出良好的鲁棒性。一阶滑模经过0.7 ms恢复到稳态值,二阶滑模经过0.6 ms恢复到稳态值,其调整时间和电压跌落相较一阶滑模均要小;当系统恢复至稳态时,二阶滑模控制下变换器的输出电压稳态误差小于一阶滑模控制。
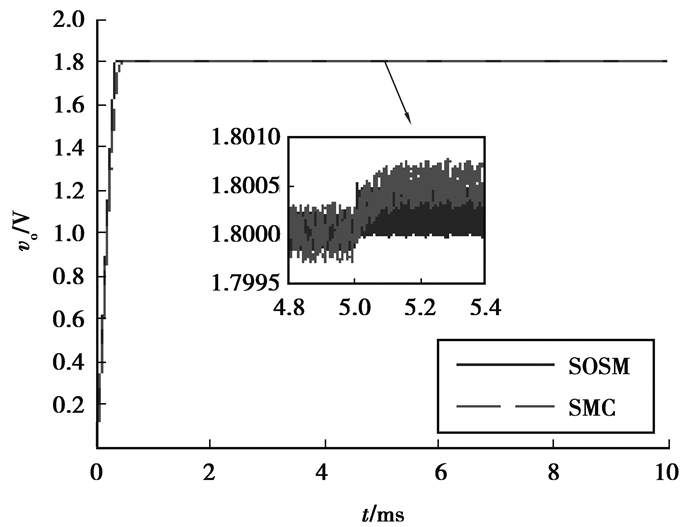
3.4 电源扰动测试在负载电阻为0.18 Ω,输出电流为10 A的条件下,令电源电压在0.005 s时从5 V跳变到10 V,得到一阶滑模和二阶滑模的输出电压波形以及测试结果数据如图 13和表 4所示。
|
图 13 电源扰动实验输出电压波形 Figure 13 Waveform of output voltage under source disturbance experiment |
| 表 4 电源扰动测试结果 Table 4 Test result under source disturbance experiment |
从图 13和表 4中可以看到,当电源电压发生5 V跳变时,一阶滑模和二阶滑模的输出均有微小偏移。一阶滑模稳态值偏移0.5 mV,二阶滑模偏移0.25 mV,都可以近似忽略,二阶滑模控制时,变换器纹波电压小于一阶滑模控制;二阶滑模控制时,系统经过0.006 ms到达新的稳态,而一阶滑模控制经过0.03 ms达到稳态,一阶滑模和二阶滑模均表现出了对电源扰动良好的鲁棒性,但二阶滑模控制的鲁棒性要优于一阶滑模控制。
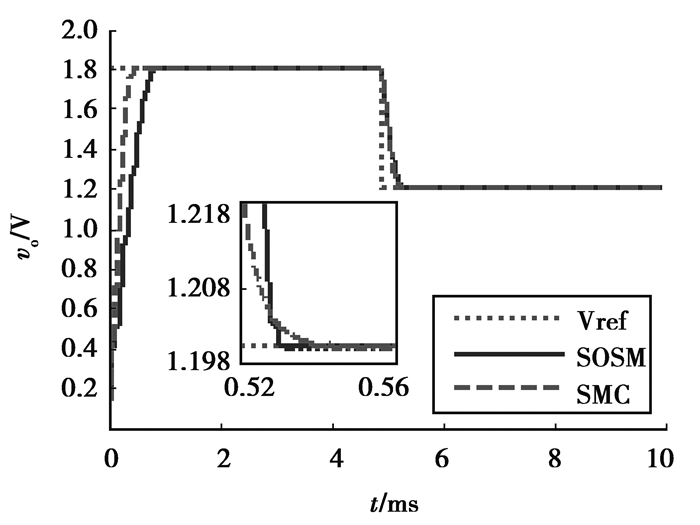
3.5 参考电压扰动测试假设在负载电阻为0.18 Ω条件下,参考电压在0.005 s时从1.8 V减小到1.2 V,得到一阶滑模和二阶滑模的输出电压波形以及扰动测试结果数据如图 14和表 5所示。
|
图 14 参考电压扰动实验输出电压波形 Figure 14 Waveform of output voltage under voltage reference disturbance experiment |
| 表 5 参考电压扰动测试结果 Table 5 Test result under voltage reference disturbance experiment |
从图 14和表 5可以看到,参考电压从1.8 V突变到1.5 V时,二阶滑模控制的调整时间为0.30 ms,一阶滑模控制的调整时间为0.45 ms,二阶滑模控制相比于一阶滑模控制表现出更快的动态响应;同时二阶滑模控制下的变换器输出电压稳态误差与纹波电压均小于一阶滑模控制。
4 结论针对同步Buck变换器设计了基于改进次优算法的二阶滑模控制器。与一阶滑模控制需要同时测量输出电压和电容电流相比,设计的二阶滑模控制器只需测量输出电压即可实现对变换器的控制,不需要使用电流互感器。采用滞环改进的次优算法在输出达到稳态时,根据Buck变换器的工作特性计算了滞环环宽,可有效限制开关频率。通过仿真,在启动性能、负载扰动和电源扰动的情况下与一阶滑模进行对比,证明了设计的二阶滑模控制器保留了传统滑模控制器的鲁棒性,并且在抵抗扰动方面和控制精度方面表现出优于一阶滑模的特点,但其启动性能受负载影响较大。
| [1] | Sreedhar J. Basavaraju D B. Design and Analysis of Synchronous Buckconverter for UPS Application//2016 2nd International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB). Califorina, USA: IEEE, 2016: 573-579. |
| [2] | Yuan R, Singh S P, Kazama T. A practical switching time model for synchronous buck converters//2016 IEEE Applied Power Electronics Conference and Exposition (APEC). Califorina, USA: IEEE, 2016: 1585-1590. |
| [3] |
陈亚爱, 李卫海, 周京华.
同步Buck变换器的控制技术综述[J]. 电气应用, 2010, 29(8): 32–36.
CHEN Yaai, LI Weihai, ZHOU Jinghua. Overview of control technology for synchronous Buck converter[J]. Electrotechnical Application, 2010, 29(8): 32–36. (in Chinese) |
| [4] | Wang J Min, Wu S T. Sensorless control scheme for synchronousbuck converter[J]. IET Circuits, Devices & Systems, 2016, 10(3): 181–191. |
| [5] | Larrea I, Seshagiri S. Voltage Mode SMC of DC-DC Buck Converters//2016 IEEE 25th International Sym posium on Industrial Electronics (ISIE). Califorina: IEEE, USA, 2016: 534-539. |
| [6] |
乐江源, 谢运祥, 洪庆祖, 等.
Boost变换器精确反馈线性化滑模变结构控制[J]. 中国电机工程学报, 2011, 31(30): 16–23.
LE Jiangyuan, XIE Yunxiang, HONG Qingzu, et al. Sliding mode control of boost converter based on exact feedback linearization[J]. Proceedings of the CSEE, 2011, 31(30): 16–23. (in Chinese) |
| [7] |
刘卓然, 许海平, 张祖之, 等.
Buck类DC/DC变换器状态反馈精确线性化恒流控制方法[J]. 中国电机工程学报, 2012, 37(2): 628–634.
LIU Zhuoran, XU Haiping, ZHANG Zuzhi, et al. A novel scheme of constant current control strategy based on state feedback linearization for buck-derived DC/DC converter[J]. Proceedings of the CSEE, 2012, 37(2): 628–634. (in Chinese) |
| [8] |
周国华, 许建平.
开关变换器调制与控制技术综述[J]. 中国电机工程学报, 2014, 34(6): 815–831.
ZHOU Guohua, XU Jianping. A review of modulation and control techniques for switching converters[J]. Proceedings of the CSEE, 2014, 34(6): 815–831. (in Chinese) |
| [9] |
刘文军, 周龙, 唐西胜, 等.
基于改进型滑模观测器的飞轮储能系统控制方法[J]. 中国电机工程学报, 2014, 34(1): 71–78.
LIU Wenjun, ZHOU Long, TANG Xisheng, et al. Research on FESS Control Based on the Improved Sliding-mode Observer[J]. Proceedings of the CSEE, 2014, 34(1): 71–78. (in Chinese) |
| [10] | Alberto C, Beniamino G. Sliding mode control for DC/DC converters//51st IEEE Conference on Decision and Control. Hawaii, USA: IEEE, 2012: 7088-7094. |
| [11] |
倪雨, 许建平, 于海坤, 等.
控制受限滑模控制Buck变换器设计[J]. 中国电机工程学报, 2010, 30(18): 26–32.
NI Yu, XU Jianping, YU Haikun, et al. Design of sliding mode control buck converter with bounded input[J]. Proceedings of the CSEE, 2010, 30(18): 26–32. (in Chinese) |
| [12] |
倪雨, 许建平, 王金平, 等.
滞环调制全局滑模控制Buck变换器设计[J]. 中国电机工程学报, 2010, 30(21): 1–6.
NI Yu, XU Jianping, WANG Jinping, et al. Design of Global Sliding Mode Control Buck Converter With Hysteresis Modulation[J]. Proceedings of the CSEE, 2010, 30(21): 1–6. (in Chinese) |
| [13] |
李雪冰, 马莉, 丁世宏.
一类新的二阶滑模控制方法及其在倒立摆控制中的应用[J]. 自动化学报, 2015, 41(1): 193–202.
LI Xuebing, MA Li, DING Shihong. A new second-order sliding mode control and its application to inverted pendulum[J]. Acta Automatica Sinica, 2015, 41(1): 193–202. (in Chinese) |
| [14] |
孙宜标, 杨雪, 夏加宽.
采用鲁棒微分器的永磁直线同步电机二阶滑模控制[J]. 中国电机工程学报, 2007, 27(33): 6–10.
SUN Yibiao, YANG Xue, XIA Jiakuan. Second order sliding mode control for PMLSM using robust differentiator[J]. Proceedings of the CSEE, 2007, 27(33): 6–10. (in Chinese) |
| [15] |
潘月斗, 陈泽平, 郭映维.
感应电机二阶滑模次优算法定子磁链观测器设计[J]. 控制理论与应用, 2015, 32(5): 641–645.
PAN Yuedou, CHEN Zeping, GUO Yingwei. Design of second order sliding-mode sub-optimal algorithm stator flux observer for induction motot[J]. Control Theory and Applications, 2015, 32(5): 641–645. (in Chinese) |
| [16] |
吴宇, 皇甫宜耿, 张琳, 等.
大扰动Buck-Boost变换器的鲁棒高阶滑模控制[J]. 中国电机工程学报, 2015, 35(7): 1740–1748.
WU Yu, HUANGFU Yigeng, ZHANG Lin, et al. A robust high order sliding mode for buck-boost converters with large disturbances[J]. Proceedings of the CSEE, 2015, 35(7): 1740–1748. (in Chinese) |
| [17] |
皇甫宜耿, 卓生荣, 王小飞, 等.
一种基于STD的Buck变换器滑模控制[J]. 西北工业大学学报, 2016, 34(4): 663–668.
HUANGFU Yigeng, ZHUO Shengrong, WANG Xiaofei, et al. A STD based sliding mode control design for DC-DC buck converter[J]. Proceedings of the CSEE, 2016, 34(4): 663–668. (in Chinese) |
| [18] | Leyva R, Maksimovic D, Ling R. Second-order sliding-mode controller for higher-order DC-DC converters//2014 IEEE 15th Workshop on Control and Modeling for Power Electronics (COMPEL). Califorina, USA: IEEE, 2014: 1-7. |
| [19] | Ling R, Maksimovic D, Leyva R. Second-Order Sliding-Mode Controlled Synchronous BuckDC-DC Converter[J]. IEEE Transactions on Power Electronics, 2015, 31(3): 2539–2549. |
| [20] |
王江, 曾启明.
非线性奇异摄动系统的二阶滑模控制[J]. 天津大学学报, 2004, 37(6): 520–526.
WANG Jiang, TSANG Kaiming. Second order sliding mode control in nonlinear singular perturbation system[J]. Journal of Tianjin University, 2004, 37(6): 520–526. (in Chinese) |
| [21] | Defoort, Michael, Thierry, et al. A novel higher order sliding mode control scheme[J]. Systems & Control Letters, 2009, 58(2): 102–108. |
| [22] | Bartolini G, Pisano A, Punta E, et al. A survey of applications of second-order sliding mode control to mechanical systems[J]. International Journal of Control, 2003, 76(9-10): 875–892. DOI:10.1080/0020717031000099010 |
| [23] | Bartolini G, Pisano A, Usai E. An improved second-order sliding-mode control scheme robust against the measurement noise[J]. IEEE Transactions on Automatic Control, 2004, 49(10): 1731–1737. DOI:10.1109/TAC.2004.835395 |
 2018, Vol. 41
2018, Vol. 41

