2. 重庆大学 通信工程学院, 重庆 400044
2. College of Communication Engineering, Chongqing University, Chongqing 400044, P. R. China
随着无线网络的高速发展,无线定位技术受到了产业界的广泛关注,已经在机器人导航、地理路由、公共安全、环境监测和车辆跟踪等领域得到不断发展[1-2]。由于基于接收信号强度(RSS,received signal strength)[3]的无线定位技术只需要无线收发器,利用现有的无线网络设备,以软件的方式定位,成本低、容易实现,已经在定位领域广泛应用。
随着测量理论的发展,基于压缩感知(CS,compressive sensing)[4-6]的定位算法是定位领域的研究热点之一。压缩感知通过对感知区域的网格化,把多目标定位问题转化为稀疏信号的重构问题。传感器节点不需要根据传统的奈奎斯特采样定理高速采样数据,而只需采集少量的感知数据,因此,简单、廉价的传感器即可满足定位系统的硬件要求。融合中心计算能力强、不受信号能量限制,因此数据的重构在融合中心完成。
相继有众多的学者提出了一系列压缩感知目标定位方法。文献[7]通过将待定位区域离散为N个网格,将目标所在的网格位置建模为K稀疏的N维向量,并通过贪婪匹配追踪(GMP,greedy matching pursuit)重构稀疏向量。文献[8-10]研究了基于RSS和压缩感知的室内定位技术,提出了基于采样值预处理和l1范数优化的多目标定位技术,对于目标不在网格中心的情况,将候选定位结果集的中心作为目标的估计位置,造成估计误差。文献[11]利用压缩感知建模将无线系统的通信开销从M×K降低到M(M是传感器节点数目,K是目标个数),同时提出了基于迭代回溯的定位算法以提高目标不在网格中心的定位精度,但系统性能容易受噪声影响。文献[12]提出了一种能量约束贝叶斯压缩感知检测算法,改善了无线传感器网络能量受限问题,但检测性能稍差。
基于压缩感知理论,针对多目标定位问题,以提高定位的准确度为目标,提出了一种基于交替迭代的压缩感知多目标定位方法。同时,以电力系统室内巡检场景为实验场所验证了将该方法应用于实际场景的有效性。
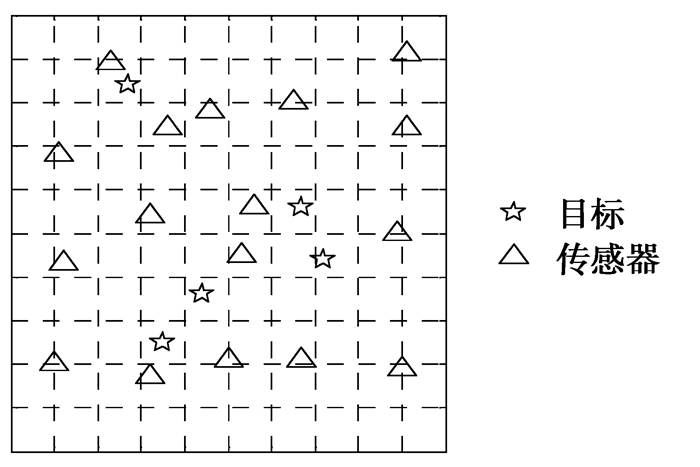
1 系统建模 1.1 系统模型图 1给出了基于压缩感知理论定位的系统模型。该模型中,定位区域为一方形区域,方形区域被均匀地划分为N个离散网格。M个位置已知的传感器以及K个未知的目标位置被随机地布设在这些网格中。此时,多目标定位问题可以理解为通过传感器接收的信号强度确定目标位于哪些网格中。
|
图 1 基于压缩感知定位的系统模型 Figure 1 System model of localization basued on compressive sensing theory |
单个目标以T为周期独立且不同步地发射信号,同时传感器收集这些信号。一个周期结束后,传感器分别将各自收到的信号强度作累加,并发送给数据融合中心,数据融合中心运行算法完成对数据的重构,确定目标在网格中的具体位置。
1.2 信号衰减模型信号在传输过程中,由于障碍物遮挡和多径衰落等因素的影响,信号强度随距离增大产生衰落。统计实验结果表明,平均接收信号强度与信号传输距离之间的函数关系可以表示为[13]
| $ \mathit{\bar P}{\rm{ = }}{\mathit{P}_{\rm{0}}}{\rm{ - 10}}{\mathit{n}_\mathit{p}}{\rm{lg(}}\mathit{D}{\rm{/}}{\mathit{D}_{\rm{0}}}{\rm{), }} $ | (1) |
式中:P为平均接收信号强度,单位为dBm;参考传输距离D0,接收的信号强度为P0;np为路径衰减指数,一般取2~4;D为信号实际传输距离。
因此,第m个传感器接收到的第n个网格中的目标发出的信号强度为
| $ {\mathit{P}_{\mathit{m}{\rm{, }}\mathit{n}}}{\rm{ = }}{\mathit{P}_{\rm{0}}}{\rm{ - 10}}{\mathit{n}_\mathit{p}}{\rm{lg(}}{\mathit{D}_{\mathit{m}{\rm{, }}\mathit{n}}}{\rm{/}}{\mathit{D}_{\rm{0}}}{\rm{), }} $ | (2) |
式中:Pm, n为第m个传感器接收到的第n个网格中的目标发出的信号强度;Dm, n为第m(1≤m≤M)个传感器和第n(1≤n≤N)个网格中目标的欧式距离,
| $ {\mathit{D}_{\mathit{m}{\rm{, }}\mathit{n}}}{\rm{ = }}\sqrt {{{{\rm{(}}{\mathit{x}_\mathit{m}}{\rm{ - }}{\mathit{x}_\mathit{n}}{\rm{)}}}^{\rm{2}}}{\rm{ + (}}{\mathit{y}_\mathit{m}}{\rm{ - }}{\mathit{y}_\mathit{n}}{{\rm{)}}^{\rm{2}}}} {\rm{, }} $ | (3) |
式中:(xm, ym)为第m个传感器的坐标;(xn, yn)表示位于第n个网格的目标的坐标。
最后,为了模拟环境中噪声的影响,研究对测量结果叠加了高斯白噪声。
2 传统压缩感知定位算法压缩感知定位算法可以描述为:已知测量矩阵Φ∈RM×N(M≪N)和待重构信号X∈RN在采用该测量矩阵时的线性测量值Y∈RN,重构出未知信号X。其中,测量值Y为每个传感器感知到的一个周期内的无线信号强度之和构成的矩阵,测量矩阵Φ为传感器感知的目标在每个网格的无线信号强度构成的矩阵,它们之间的关系为
| $ {\mathit{\boldsymbol{Y}}_{\mathit{M}{\rm{ \times 1}}}}{\rm{ = }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{M}{\rm{ \times }}\mathit{N}}}{\mathit{\boldsymbol{X}}_{\mathit{N}{\rm{ \times 1}}}}{\rm{。}} $ | (4) |
压缩感知定位算法分为2个阶段[14-15]:压缩采样阶段和信号重构阶段。压缩采样阶段得到测量结果Y,重构阶段完成根据测量矩阵Φ和测量结果Y的信号重构。
2.1 压缩采样φ为Φ中的元素,它是第m个传感器收到的第n个网格中目标的信号强度
| $ {\mathit{\varphi }_{\mathit{m}{\rm{, }}\mathit{n}}}{\rm{ = }}{\mathit{P}_{\mathit{m}{\rm{, }}\mathit{n}}}{\rm{, 1}} \le \mathit{m} \le \mathit{M}{\rm{, 1}} \le \mathit{n} \le \mathit{N}{\rm{, }} $ | (5) |
系统的压缩采样过程为
| $ \left[\begin{array}{l} {\mathit{y}_{\rm{1}}}\\ {\mathit{y}_{\rm{2}}}\\ \; \vdots \\ {\mathit{y}_\mathit{M}} \end{array} \right]{\rm{ = }}\left[{\begin{array}{*{20}{c}} {{\mathit{P}_{{\rm{1, 1}}}}}&{{\mathit{P}_{{\rm{1, 2}}}}}& \cdots &{{\mathit{P}_{{\rm{1, }}\mathit{N}}}}\\ {{\mathit{P}_{{\rm{2, 1}}}}}&{{\mathit{P}_{{\rm{2, 2}}}}}& \cdots &{{\mathit{P}_{{\rm{2, }}\mathit{N}}}}\\ \vdots & \vdots &{}& \vdots \\ {{\mathit{P}_{\mathit{M}{\rm{, 1}}}}}&{{\mathit{P}_{\mathit{M}{\rm{, 2}}}}}& \cdots &{{\mathit{P}_{\mathit{M}{\rm{, }}\mathit{N}}}} \end{array}} \right]\left[\begin{array}{l} {\mathit{x}_{\rm{1}}}\\ {\mathit{x}_{\rm{2}}}\\ \; \vdots \\ {\mathit{x}_\mathit{N}} \end{array} \right]{\rm{, }} $ | (6) |
式中,X是稀疏度为K的N维向量,当第n(1≤n≤N)个网格中有目标时,xn=1,否则,xn=0。传感器的感知结果Y为测量矩阵Φ与X的乘积,ym(1≤m≤M)为第m个传感器在一个周期T内接收到的目标发射的信号强度之和。这样,多目标定位问题就通过压缩感知理论被有效转化为根据M个测量结果的N维稀疏信号重构问题。
2.2 信号重构重构阶段主要完成由测量结果Y重构信号X。Φ是一个M×N矩阵,方程的个数远小于未知数的个数,这是一个欠定线性方程组,无确定解。由于N远大于K,因此信号是K稀疏的。如果Φ满足约束等距性条件(RIP,restrict isometry property)[16],那么,测量值Y通过l1范数最优化问题可以精确重构信号X
| $ {\mathit{\boldsymbol{X}}_{\mathit{est}}}{\rm{arg}}\;{\rm{min||}}\mathit{\boldsymbol{X}}{\rm{|}}{{\rm{|}}_{\rm{1}}}{\rm{, s}}{\rm{.t}}{\rm{.}}\;\mathit{\boldsymbol{Y}}{\rm{ = }}\mathit{\boldsymbol{ \boldsymbol{\varPhi} X}}{\rm{, }} $ | (7) |
Feng等[8-10]提出了对矩阵进行Orth预处理的方法,从而使新的测量矩阵满足RIP性质。Orth预处理过程描述如下
| $ \mathit{\boldsymbol{Y'}}{\rm{ = }}\mathit{\boldsymbol{TY}}{\rm{, }} $ | (8) |
Y′为预处理后的接收矩阵。T=QA+,其中A为测量矩阵Φ,(·)+表示矩阵的伪逆变换,Q=orth(AT)T,orth(·)表示矩阵规范正交化操作,(·)T表示矩阵的转置算子。处理后的矩阵Q为正交变换矩阵,较好地满足了RIP性质,能够提高稀疏信号的重构性能,从而提升多目标定位的准确度。
3 改进的多目标定位算法传统压缩感知定位算法在重构阶段使用和测量矩阵相同的重构矩阵,而测量矩阵是在压缩采样的实际过程中得到的。因此1)若目标位置在网格中心,根据式(2)构造出的重构矩阵即为准确的测量矩阵;2)若目标不在网格中心,根据式(2)构造出的重构矩阵则和实际的测量矩阵有偏差,不能准确定位目标位置。同时,由于噪声等环境因素的影响,目标有可能被定位在相邻的网格,从而增大定位误差。
笔者提出一种采用粗定位和精定位相结合的方法以改善上述缺点。该方法的主要思路为:粗定位阶段,根据式(2)构造出的重构矩阵Φ和传统压缩感知算法得到粗略的目标初始位置;精定位阶段,采用交替迭代方法不断修正重构矩阵,因此重构矩阵能够逐步接近实际测量矩阵。交替迭代过程使用菱形搜索对目标在网格中的位置不断搜索,提高定位的准确度。
交替迭代方法的核心思想为:首先选取一个初始的目标网格(该网格中可能存在目标),进行一次菱形搜索,选择搜索点中重构误差最小的点作为新的目标迭代位置,根据这个位置修正一次重构矩阵;然后选取下一个初始的目标网格进行一次菱形搜索,根据搜索结果修正重构矩阵;继续选取网格,直到搜索完所有可能存在目标的网格,至此,一次迭代完成。重复以上迭代过程,不断调整目标位置,使重构矩阵逐步趋近于实际的测量矩阵,直到迭代次数满足预设的最大迭代次数或所有可能存在目标的网格小菱形搜索模式结束。
菱形搜索方法使用2种搜索模式,一是大菱形搜索模式(LDSP,large diamond search pattern),由9个检测点组成,二是由5个检测点形成的小菱形搜索模式(SDSP,small diamond search pattern),如图 2所示。

|
图 2 菱形搜索模式 Figure 2 Diamond Search mode |
菱形搜索方法的主要过程为:选择粗定位阶段中可能存在目标的网格,在该网格附近不断搜索,直到找到重构误差最小的位置。根据定位精度要求,确定搜索步长g,即将可能存在目标的网格区域划分为更细小的网格。在可能存在目标的网格附近首先使用搜索范围较大的LDSP进行粗定位。假设目标依次位于相应的9个位置点,计算相应的重构矩阵,得到重构信号以及重构误差,9个点中重构误差最小的点即为下一次菱形搜索的搜索中心,一次搜索完成。继续重复以上搜索过程,进一步缩小目标所在区域范围。在搜索过程中,LDSP被重复使用,直到重构误差最小的点出现在LDSP的中心,这时最优匹配点区域找到,然后再用SDSP进行更精细的定位。最后SDSP的5个点中重构误差最小的点即为最终的目标位置。
理想的重构结果和实际的重构结果的偏差
| $ {\mathit{E}_\mathit{n}}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}}\;\; {\left| {{\mathit{x}_\mathit{n}}} \right|{\rm{, }}\;\;\;\;{\mathit{x}_\mathit{n}} \le {\rm{0}}{\rm{.5, }}}\\ {\left| {{\mathit{x}_\mathit{n}}{\rm{ - 1}}} \right|{\rm{, }}\;\;{\mathit{x}_\mathit{n}}{\rm{ > 0}}{\rm{.5, }}} \end{array}\;\;\;\;\;\;\;\;{\rm{1}} \le \mathit{n} \le \mathit{N}{\rm{, }}} \right. $ | (9) |
重构的信号中,xn值越大,该网格存在目标的概率越大。因此,只有大于阈值TH的重构元素可能存在目标,只对它们进行精定位能够降低算法的复杂度。
设第n个网格中的目标位置(Y(n, 1), Y(n, 1))初值为网格中心(XGn, YGn),网格宽度为G,g为进一步细分的网格宽度,即搜索步长。第i次迭代时(i=1, 2, 3…)目标的位置调整为
| $ \left( {{\mathit{X}_{{\rm{(}}\mathit{n}{\rm{, }}\mathit{i}{\rm{ + 1)}}}}{\rm{, }}{\mathit{Y}_{{\rm{(}}\mathit{n}{\rm{, }}\mathit{i}{\rm{ + 1)}}}}} \right){\rm{ = }}\left( {{\mathit{X}_{{\rm{(}}\mathit{n}{\rm{, }}\mathit{i}{\rm{)}}}}{\rm{, }}{\mathit{Y}_{\mathit{n}{\rm{, }}\mathit{i}}}} \right){\rm{ + }}\mathit{g}{\rm{ \times grid, }} $ | (10) |
grid为菱形模式的格点。大菱形搜索模式的格点为
| $ {\rm{grid = }}\left\{ {\left( {{\rm{0, - 2}}} \right)\left( {{\rm{ - 1, - 1}}} \right)\left( {{\rm{1, - 1}}} \right)\left( {{\rm{ - 2, 0}}} \right)\left( {{\rm{0, 0}}} \right)\left( {{\rm{2, 0}}} \right)\left( {{\rm{ - 1, 1}}} \right)\left( {{\rm{1, 1}}} \right)\left( {{\rm{0, 2}}} \right)} \right\}{\rm{, }} $ | (11) |
小菱形搜索模式的格点为
| $ {\rm{grid = }}\left\{ {\left( {{\rm{0, - 1}}} \right)\left( {{\rm{ - 1, 0}}} \right)\left( {{\rm{0, 0}}} \right)\left( {{\rm{1, 0}}} \right)\left( {{\rm{0, 1}}} \right)} \right\}{\rm{, }}\ $ | (12) |
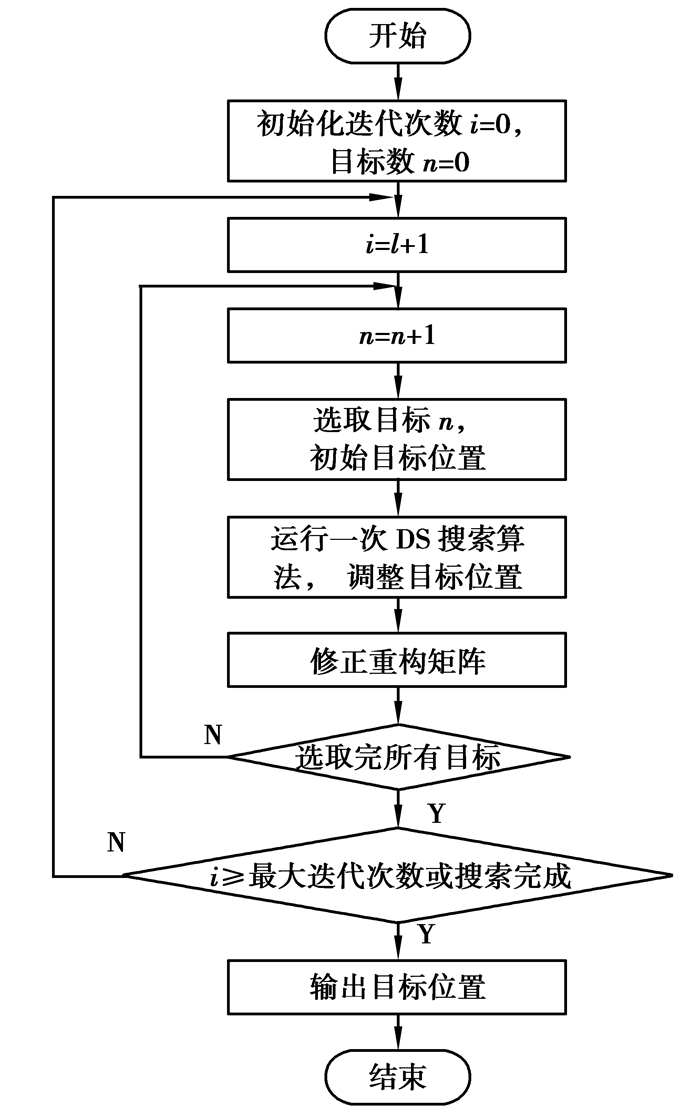
交替迭代方法的流程图如图 3所示,算法的步骤描述如下
|
图 3 交替迭代方法流程图 Figure 3 Flow chart of multiple target alternate iteration approache |
步骤1:从粗定位结果中选择一个可能存在目标的网格,进行目标位置初始化,(X(n, 1), Y(n, 1))=(XGn, YGn)。
步骤2:计算重构误差
步骤3:采用菱形搜索模式,将目标分别调整到相应位置,依次计算重构矩阵、重构信号以及重构误差。选则重构误差最小的点,调整目标位置。特别注意的是:若上一次迭代的重构误差最小值所对应的点位于中心位置,则本次迭代采用SDSP搜索;若上一次迭代采用SDSP搜索,则该目标搜索完成,目标位置不进行调整。
步骤4:根据调整的位置修正重构矩阵。
步骤5:选取下一个可能存在目标的网格,重复步骤1到步骤4,直到完成所有大于阈值TH的网格点搜索,一次迭代完成。
步骤6:重复步骤1到步骤5,直到迭代次数满足预设的最大迭代次数或所有可能存在目标的网格小菱形搜索模式结束。
步骤7:输出定位结果。
研究使用交替迭代不断修正重构矩阵,提高了目标不在网格中心和定位结果在实际目标相邻网格情况下的定位准确度,减轻目标间的相互干扰。同时,该方法的定位精度由菱形搜索的步长决定,首先选用LDSP进行粗定位,不会导致搜索一开始就会偏向某个区域,使搜索过程陷于局部最小,然后选用SDSP模式进行精定位,提高了定位准确度。此外,菱形搜索方法不局限于在一个网格内搜索,对定位结果在实际目标相邻网格的情况十分有效。
4 仿真及实验针对提出的多目标定位方法,采用Matlab进行理论的仿真分析,分析算法性能以及当接收信号强度受到外界干扰时,该算法的鲁棒性。同时,以重庆电力系统实际室内运维巡检区域为测试场所,验证该算法在实际环境下的实用性和抗干扰性。
4.1 理论仿真分析首先,对仿真参数进行描述。仿真工具为Matlab,重构算法为BP算法。定位区域大小为50 m×50 m,划分14×14共196个网格。传感器个数M的值为49,最大迭代次数为6。信号强度-距离模型参数:P0=-40 dBm,np=2,D0=1。
4.1.1 目标位于网格中心图 4给出了目标数为15,目标位于不同的网格中心,系统在无噪、SNR=5 dB和SNR=20 dB 3种情况下的定位结果。从仿真结果可见:在无噪声情况下,算法能很好的定位目标位置;噪声越大,定位效果越差,但都能定位到目标所在网格或相邻网格;目标越集中,由于目标间的互相影响,定位效果也越差。

|
图 4 目标位于网格中心时不同信噪比下的定位结果 Figure 4 Localization result when targets are in the center of the grid under different SNR |
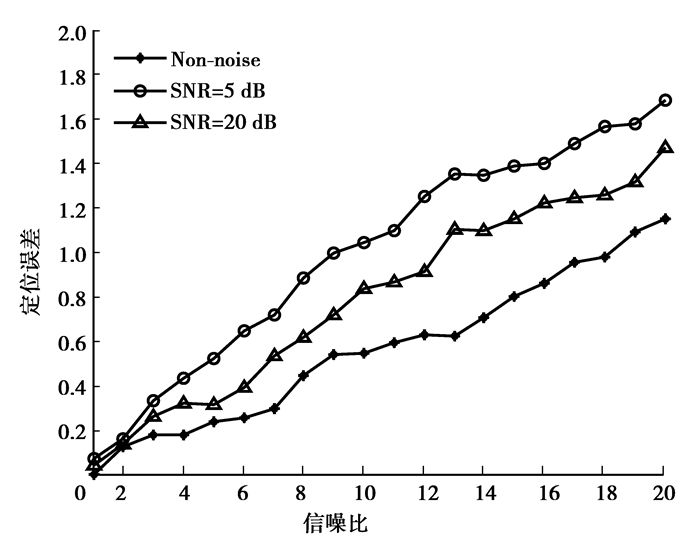
重复200次蒙特卡洛实验,通过式(3)计算目标原始坐标与恢复后的坐标之间的距离,通过求均值得到在不同信噪比下定位误差随目标数目变化曲线(如图 5所示)。从图 5可以看出:随着目标个数的增多,信号稀疏度变小,平均定位误差也逐渐变大;随着噪声的增大,定位误差也会变大。在无噪情况下,定位算法系统对20个目标的平均定位误差约为1.2 m;在低噪声干扰下,定位算法对20个目标的平均定位误差约为1.5 m;在强噪声干扰下,定位算法对20个目标的平均定位误差约为1.7 m。
|
图 5 不同信噪比下定位误差随目标数目变化曲线 Figure 5 Curve of laclization error changing with the target unmber under different SNR |
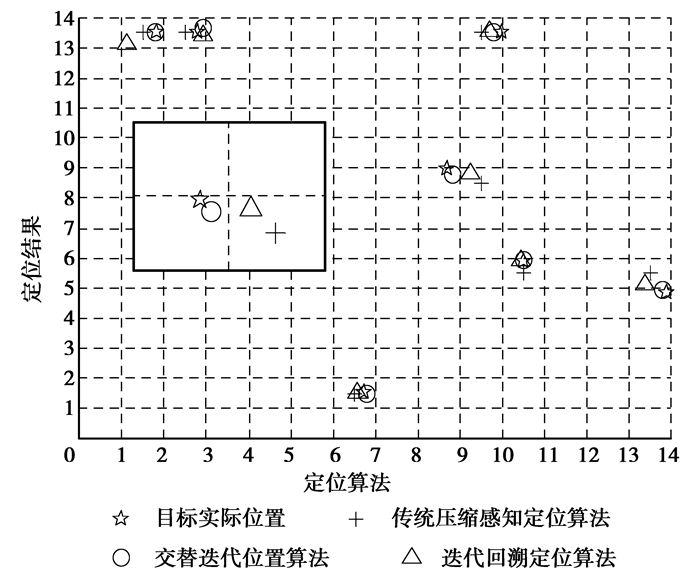
对于目标不在网格中心的情况,图 6给出了目标数为7,系统在15 dB信噪比条件下,分别使用迭代回溯算法[11]、传统压缩感知算法和研究改进算法3种方法的定位结果。从图 6可以看出,传统的压缩感知算法只能对网格中心的目标准确定位,目标不位于网格中心时,定位误差较大;迭代回溯算法能比较准确定位不在网格中心的目标,但其只能在可能存在目标的网格内搜索,不能处理定位结果不在实际目标相邻的网格情况;算法对可能存在目标的网格附近进行搜索,不受网格的限制,因此更准确。同时,在交替迭代过程中,由于不断地更新目标的位置,减轻了相邻目标间的相互干扰对定位精度的影响。
|
图 6 不同定位算法定位结果对比 Figure 6 Comparison of localization results of different localization algorithms |
研究设计了一个室内巡检定位系统以验证提出的方法应用于电力系统室内巡检定位的有效性,该系统包括无线信号发射器、无线信号接收器和服务器,它们之间采用串口通信。其中,无线信号发射器和无线信号接收器采用集收发功能于一体的射频收发器CC1101模块(如图 7所示)。该模块具有成本低、功耗小、工作频带可调、高接收灵敏度等优点,符合本系统需要。服务器采用联想IBM服务器,配备2.4 G频率的Intel E5-2630 V3 CPU以及16G RAM。

|
图 7 CC1101无线模块 Figure 7 Wireless module of CC1101 |
选取重庆某电力公司的室内运维巡检区域作为实验场所,如图 8所示。图 8中:(a)为给自动化机房提供不间断电源以及在失电时提供应急电源的UPS电源室;(b)为自动化系统不间断运行维护室。对以上2个室内场所的巡检,是及时发现电力自动化设备的缺陷,保障电力系统稳定运行的关键。实验及环境参数为:(a)场所大小为10 m×5 m、划分8×4共32个网格、布设8个CC1101无线模块作为无线信号接收器;(b)场所大小为10 m×15 m、划分8 ×12共96个网格、布设15个无线信号接收器、2个区域相邻但独立定位;接收器不能与待定位目标相隔太近,同时尽可能均匀分布;无线信号发射器发射信号强度为1 dBm;目标数为1,即单个巡检人员携带射频收发器CC1101进行实验;考虑运算速度和人员巡检速度,定位周期为4 s。

|
图 8 实验场所 Figure 8 Experiment place |
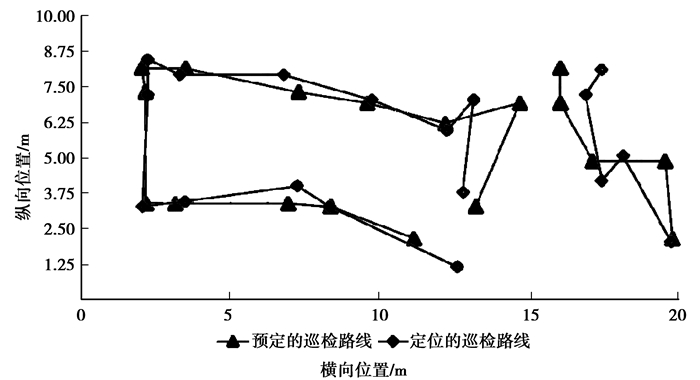
根据单目标定位结果,得到定位的巡检路线和预定巡检路线对比(如图 9所示)。从图 9可以看出:该定位方法取得了较好的室内巡检人员定位结果,在噪声干扰和障碍物的遮挡下,平均定位误差约为0.8 m,达到了定位精度要求。笔者方法能记录相应时刻巡检人员的位置,同时生成巡检路线,保证了巡检的真实性。
|
图 9 预定的巡检路线与定位的巡检路线对比 Figure 9 Comparision of scheduled inspection route and localization in spection route |
笔者提出了一种将交替迭代应用于压缩感知多目标定位算法以提高多目标定位的精确度。仿真结果显示本方法改善了目标不在网格中心的定位精度,减轻了密集目标的相互影响对定位精度的干扰,多目标定位的准确度提高。同时,在电力系统实际室内巡检场所的验证实验表明,该方法能快速定位室内巡检人员的位置,记录巡检人员的巡检路线,有效提高室内定位准确度和巡检到位率。该算法的复杂度稍高,这是算法的不足之处,需要进一步展开优化工作以降低计算复杂度。
| [1] | Ren F Y, Huang H N, Lin C, et al. Wireless sensor networks[J]. Journal of Software, 2003, 14(7): 1282–1291. |
| [2] | Patwari N, Ash J N, Kyperountas S, et al. Locating the nodes:cooperative localization in wireless sensor networks[J]. Signal Processing Magazine, IEEE, 2005, 22(4): 54–69. DOI:10.1109/MSP.2005.1458287 |
| [3] | Tarrio P, Bernardos A M, Besade J A, et al. A new positioning technique for RSS-based localization based on a weighted least squares estimator[C]//Proceedings of IEEE International Symposium on Wireless Communication Systems. [S. l. ]: IEEE, 2008: 633-637. |
| [4] | Cevher V, Duarte M, Baraniuk R G, et al. Distributed target localization via spatial sparsity[C]//European Signal Processing Conference. Switzerland: Lausanne, 2008: 25-29. |
| [5] | Nikitaki S, Tsakalides P. Localization in wireless networks via spatial sparsity[C]//Signals, Systems and Computers (ASILOMAR), 2010 Conference Record of the Forty Fourth Asilomar Conference on. [S. l. ]: IEEE, 2010, 11(7): 236-239. |
| [6] |
刘凯, 余君君, 黄青华, 等.
基于压缩感知的免携带设备双目标定位算法[J]. 电子与信息学报, 2014, 36(04): 862–867.
LIU Kai, YU Junjun, HUANG Qinghua, et al. Biobject device-free localization based on compressive sensing[J]. Journal of Electronics & Information Technology, 2014, 36(04): 862–867. (in Chinese) |
| [7] | Zhang B, Cheng X, Zhang N, et al. Sparse target counting and localization in sensor networks based on compressive sensing[C]//INFOCOM, 2011 Proceedings IEEE. [S. l. ]: IEEE, 2011: 2255-2263. |
| [8] | Feng C, Au W S A, Valaee S, et al. Received-signal-strength based indoor positioning using compressive sensing[J]. IEEE Transactions on Mobile Computing, 2012, 11(12): 1 983–1 993. DOI:10.1109/TMC.2011.216 |
| [9] | Au W S A, Feng C, Valaee S, et al. Indoor tracking and navigation using received signal strength and compressive sensing on a mobile device[J]. IEEE Transactions on Mobile Computing, 2013, 12(10): 2050–2062. DOI:10.1109/TMC.2012.175 |
| [10] | Feng C, Valaee S, Tan Z, et al. Multiple target localization using compressive sensing[C]//Global Telecommunications Conference. [S. l. ]: IEEE, 2009: 1-6. |
| [11] |
何风行, 余志军, 刘海涛.
基于压缩感知的无线传感器网络多目标定位算法[J]. 电子与信息学报, 2012, 32(3): 716–721.
HE Fenghang, YU Zhijun, LIU Haitao. Multiple target localization via compressed sensing in wireless sensor networks[J]. Journal of Electronics & Information Technology, 2012, 32(3): 716–721. (in Chinese) |
| [12] |
赵春晖, 许云龙.
能量约束贝叶斯压缩感知检测算法[J]. 通信学报, 2012, 33(10): 1–6.
ZHAO Chunhui, XU Yunlong. Energy constraint bayesian compressive sensing detection algorithm[J]. Journal on Communications, 2012, 33(10): 1–6. (in Chinese) |
| [13] | Candes E, Plan Y. A probabilistic and RIPless theory of compressed sensing[J]. IEEE Transactions on Information Theory, 2011, 57(11): 7 235–7 254. DOI:10.1109/TIT.2011.2161794 |
| [14] | Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. DOI:10.1109/TIT.2006.871582 |
| [15] | Candes E, Romberg J, Tao T, et al. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489–509. DOI:10.1109/TIT.2005.862083 |
| [16] | Candes E. The restricted isometry property and its implications for compressed sensing[J]. Academie Sciences, 2006, 346(1): 589–592. |
 2018, Vol. 41
2018, Vol. 41


