地震易损性分析可以预测结构在不同等级地震作用下发生各级破坏的概率,因此,对结构的抗震设计、加固和维修决策具有重要的价值。当前,地震易损性分析在全世界得到了广泛的研究,特别是近年来,以控制地震损失和地震风险为目标的新一代基于性能的地震工程(Performance-based earthquake engineering,PBEE)正成为国际地震工程领域的研究热点。与基于性能的地震工程(PBEE)相对应,中国设计规范中“两阶段设计方法”、“三水准设防目标”的理论以及规定的具体措施等也都与基于性能的地震工程的设计理念基本一致[1]。但是,现行抗震规范对结构在大震中的抗倒塌定量设计方法和定量评价指标体系尚缺乏明确规定[2]。
随着中国城市化进程的加快,大量的钢筋混凝土RC框架结构运用于建筑工程,主要有临街商铺框架结构,底部为大空间、上部为住宅的框架结构等。汶川地震中框架结构所表现出的抗倒塌性能不甚理想[3-4],出现了大量的“短柱破坏”、“薄弱层破坏”和“强梁弱柱破坏”,表明填充墙不仅会对框架结构的刚度产生影响,还会改变框架结构的承载力性能,对框架结构的抗震研究,有必要进一步考虑填充墙的影响因素[5]。
设计了一种6层3跨的钢筋混凝土框架结构,结合实际情况设计了填充墙的4种布置方式和与之对应的4种模型工况,基于动力增量时程分析(IDA)理论和地震易损性分析理论,定量分析结构在各模型工况下的抗地震倒塌能力。
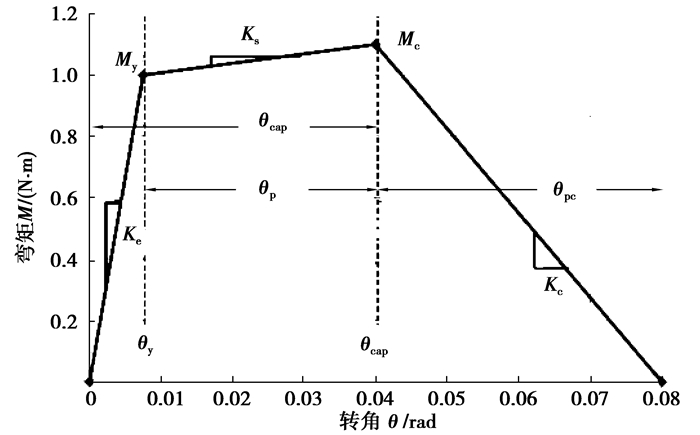
1 恢复力模型 1.1 改进IMK模型Ibarra等[6]提出了IMK(ibarra-medina-krawinkler)恢复力模型理论。IMK模型的骨架曲线为三线形,由弹性段、强化段及软化段构成,能够模拟RC梁柱的强度、刚度退化现象,模型主要由5个参数来控制结构或构件的单调行为和循环行为(各参数见图 1),分别为屈服弯矩My、初始刚度Ke、峰值弯矩Mc、屈服到峰值段塑性转角θp或硬化段刚度Ks、软化段转角θpc或软化段刚度Kc,其中,Ks=αsKe(αs为强化刚度系数),Kc=αcKe(αc为软化刚度系数)。
|
图 1 改进IMK模型骨架曲线 Figure 1 Backone curve of the modified Ibarra-Medina-Krawinkler model |
在定义恢复力模型骨架曲线时,IMK恢复力模型需先定义弹性刚度Ke,再由强化刚度系数αs和软化刚度系数αc确定硬化段及软化段的位置。相对于IMK模型所用参数,Lignos等[7]通过实验发现,采用θp(θp=θcap-θy)作为反映机构塑性变形能力的指标较采用δc/δy更精确,采用比值Mc/My作为强化指标较采用αs的随机性更小,采用θpc作为软化指标较采用的离散性更小,Lignos等在IMK模型和试验结论的基础上提出了改进IMK恢复力模型理论(如图 1所示),由该模型确定的骨架曲线误差小且更加精确稳定。
在滞回耗能方面,IMK恢复力模型采用屈服转角θy与屈服弯矩My的乘积(Et=γMyθy)表示滞回耗能,而改进IMK模型对其进行了修改,采用了屈服点至峰值点区段对应的塑性转角θp与屈服弯矩My的乘积(Et=λMyθp)表示滞回耗能。在计算各退化系数βi时,改进IMK模型在公式中引进了一个无量纲系数D(D≤1),以此来考虑正负方向加载时退化速率不对称的问题。
| $ {{\beta }_{i}}\begin{matrix} {{\left( \frac{{{E}_{i}}}{{{E}_{t}}-\sum\nolimits_{j=1}^{i}{{{E}_{j}}}} \right)}^{c}} \\ {{E}_{\rm{y}}}=\gamma {{M}_{\rm{y}}}{{\theta }_{\rm{y}}} \\ \end{matrix}\underrightarrow{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }~{{\beta }_{i}}\begin{matrix} {{\left( ~\frac{{{E}_{i}}}{{{E}_{t}}-\sum\nolimits_{j=1}^{i}{{{E}_{j}}}} \right)}^{c}}{{D}^{+/-}}~ \\ {{E}_{\rm{y}}}=\gamma {{M}_{\rm{y}}}{{\theta }_{\rm{y}}} \\ \end{matrix}。$ | (1) |
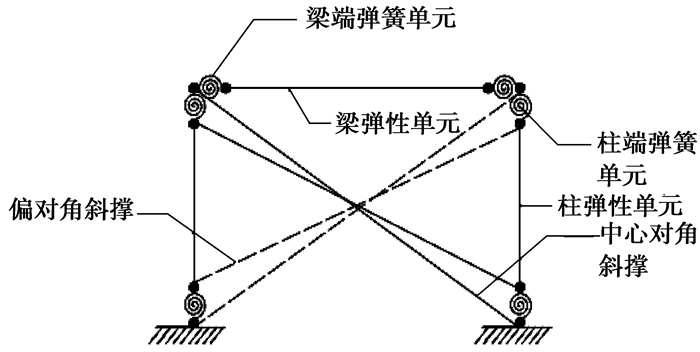
填充墙的非线性性能对填充墙RC框架结构的抗地震倒塌能力评估至关重要,文中采用双对角斜撑杆模型[9](仅受压)来模拟填充墙的非线性特性,将每一方向的中心对角斜撑(central compression-only infill strut)和偏对角斜撑(off-diagonal compression-only infill strut)置于梁柱节点之间,以模拟填充墙与框架柱之间的相互作用和填充墙的性能。模型的具体布置方式如图 2所示。
|
图 2 填充墙RC框架模型 Figure 2 The model of RC frame with infills |
通过对255个钢筋混凝土柱的分析,Haselton等对上述恢复力模型中骨架曲线的参数提出了计算公式,屈服弯矩值My由Fardis提出的公式。
| $ {{\theta }_{\rm{p}}}=0.12(1+0.55{{\alpha }_{si}}){{\left( 0.16 \right)}^{v}}{{(0.02+40{{\rho }_{sh}})}^{0.43}}{{\left( 0.54 \right)}^{0.01{{{{f}'}}_{c}}}}{{\left( 0.66 \right)}^{0.1{{s}_{n}}}}{{\left( 2.27 \right)}^{10\rho }}, $ | (2) |
| $ {{s}_{\rm{n}}}=\frac{s}{{{d}_{b}}}{{({{f}_{y}}/100)}^{0.5}}, $ | (3) |
| $ {{\theta }_{\rm{pc}}}=\left( 0.76 \right){{\left( 0.031 \right)}^{v}}{{(0.02+40{{\rho }_{sh}})}^{1.02}}\le 0.10, $ | (4) |
| $ E{{I}_{\rm{y}}}/E{{I}_{\rm{g}}}=0.065+1.05\nu, 0.2\le E{{I}_{\rm{y}}}/E{{I}_{\rm{g}}}\le 0.6, $ | (5) |
| $ {{M}_{\rm{c}}}/{{M}_{\rm{y}}}=\left( 1.25 \right){{\left( 0.89 \right)}^{v}}{{\left( 0.91 \right)}^{0.01{{{{f}'}}_{c}}}}, $ | (6) |
式中:θp为屈服点到峰值点塑性转角;Sn为纵向钢筋屈曲系数;θpc为峰值点后软化段塑性转角;EIy/EIg为有效抗弯刚度比,计算构件初始刚度Ke;Mc/My为峰值弯矩与屈服弯矩的比值;αsi为纵向钢筋滑移系数(考虑取1,不考虑取0);f′c为混凝土抗压强, N/mm2;v为构件的轴压比;ρsh为构件箍筋配筋率;ρ为纵向钢筋配筋率;S为箍筋间距;db为梁柱截面有效高度, mm;fy为纵向钢筋屈服强度, N/mm2。
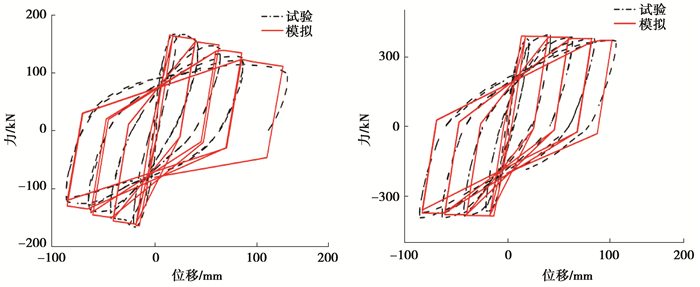
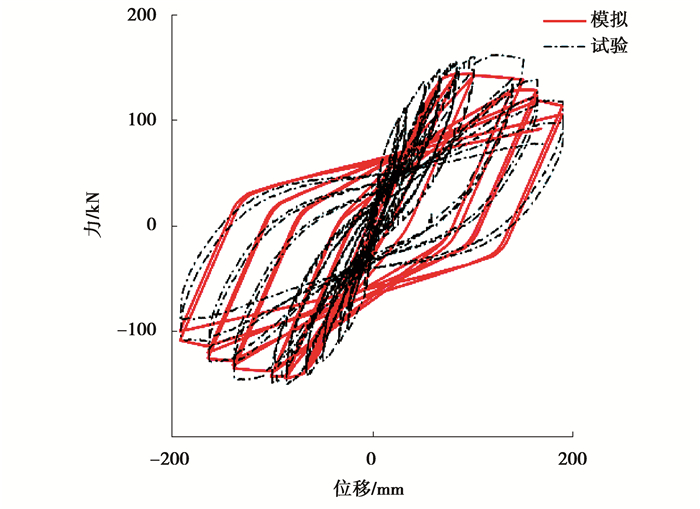
2 算例为了验证改进IMK模型对构件和结构模拟的正确性,文中从PEER[11]柱试验数据库中随机选取了Test18和Test26两根柱子进行模拟,并对文献[12]中三层三跨RC框架和文献[13]中框架填充墙的低周反复加载试验进行数值模拟。模拟基于OpenSees有限元软件,建立了RC构件、RC框架和RC框架填充墙结构的数值模型,其中,梁柱单元采用集中塑性单元。集中塑性单元由以下2部分构成:1)梁柱中部保持弹性,故梁柱中部采用弹性梁柱单元;2)破坏集中在梁柱的两端,故两端采用基于改进IMK恢复力模型的零长度弹簧单元,以模拟构件的非线性行为。填充墙采用双对角斜撑杆模型模拟,填充墙材料选用文献[13]中的混凝土空心砌块,对角斜撑采用基于峰值指向型Clough模型的杆件(Truss)单元建模。最后,通过与RC构件和整体结构的试验结果分别进行对比,验证所建立的有限元数值模型的精确实用性。模拟结果与试验结果的对比如图 3~图 5所示。
|
图 3 柱子试验与模拟对比图 Figure 3 Comparison between simulation and experiment for columns |
|
图 4 纯框架试验与模拟对比图 Figure 4 Comparison between simulation and experiment for frame |
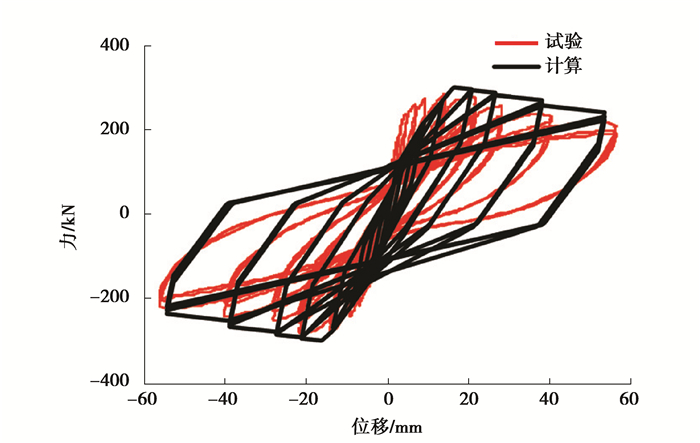
|
图 5 填充墙框架(AFKJ2)试验与模拟对比图 Figure 5 Comparison between simulation and experiment for AFKJ2 |
由图 3可知,构件正向加载时两曲线吻合较好,但负向卸载时模型的刚度比试验稍小,产生此现象的原因可能为模型本身的误差和试验误差:1)改进IMK模型为三线型恢复力模型,是理想的线性模型,其本身就存在着与实际不符的误差;2)试验中存在的安装误差、试件与作动器接触不紧密等误差,导致滞回曲线出现不对称现象,没有反映结构的真实性能,而模拟采用的改进IMK模型是对称的滞回模型,自然不能精确地与非对称的试验曲线吻合。
由图 4~图 5可知,在试验初级阶段,模型模拟的初始刚度比实际刚度小,图 5在负向卸载时的模拟刚度也偏小,产生误差的原因可能有:1)构件的真实刚度值很难确定,建模时选用的RC梁柱弹性抗弯刚度值EIy并非精确值,且结构在试验初期并没有发生屈服;2)试验存在的误差使试验结果不够准确,这一点可由图形的对称程度判断得到,改进IMK模型是对称的滞回模型,而试验所得曲线不对称,说明有误差存在,具体表现为结构在正向加载下的底部剪力值大于其在负向加载下的值,底部剪力在正向加载下的值比实际偏小,而在负向加载下却与IMK模型曲线吻合较好等;3)模拟模型中没有考虑梁柱节点的相互影响;4)改进IMK模型本身就存在误差。
分析图 3~图 5可知,RC柱、RC框架、RC框架填充墙三模型滞回曲线的走势都与对应的试验曲线基本保持一致,数值模型很好地模拟出了滞回曲线的捏拢效应,对结构非线性行为的模拟较好,对强度、刚度退化行为的模拟也较好,对比结果说明所建数值模型对构件及框架的模拟是精确实用的。
3 结构的抗倒塌能力分析 3.1 结构设计按照中国规范采用PKPM软件设计一种6层3跨RC框架结构,模型拟位于四川省汶川县某地,结构抗震设防烈度为8度(0.2 g),地震分组为第二组,场地类别为Ⅱ类,考虑填充墙的影响,周期折减系数取为0.7。文中对所建模型的第三榀框架进行结构侧向抗倒塌分析,结构平面图、立面图和梁柱尺寸及配筋见图 6(a)~图 6(c),其中柱箍筋为φ8@100,梁箍筋为φ8@100/200,结合实际情况设计了图 6(d)~图 6(g)所示的4种模型工况,不同工况下填充墙的布置方式不同。
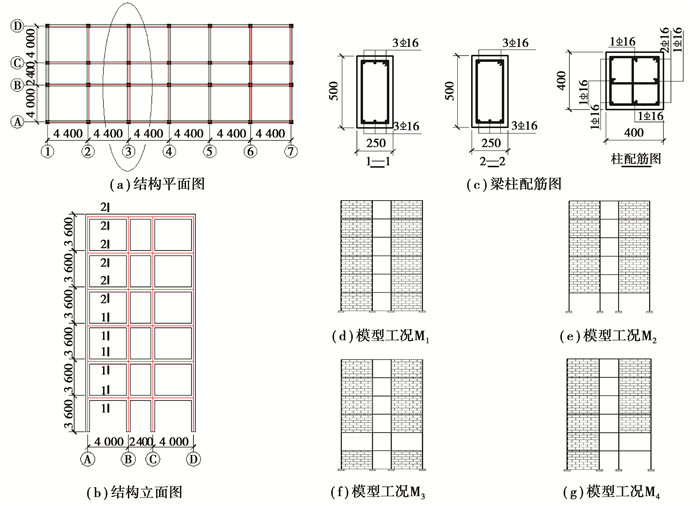
|
图 6 框架结构设计示意图与模型工况示意图 Figure 6 The frame structure reinforcement drawing and the diagrammatic sketch of model condition |
选取FEMA P-695[14]推荐的22组(44条)远场地震波作为IDA分析的地震动记录集,用结构第一周期对应的谱加速度Sa(T1, 5%)/g来表示地震动强度值IM,选取结构层间位移角θmax(rad)作为结构损伤性能参数DM。地震波的调幅方法采用Hunt & Fill方法。结构侧向倒塌点的判断选用IM-DM混合准则,即FEMA350[15]建议的准则。依据上述IDA分析准则,分别对4种工况下的模型进行44条地震波的IDA分析。
图 7所示的IDA曲线汇总图,是将各模型工况下44条地震波的IM-DM曲线绘制于同一坐标系所得。M1、M3的IDA曲线分布较M2、M4分散,可更全面地反映地震动记录特性;M1中曲线末端所对应的地震峰值加速度值Sa分布均匀且范围较大,说明结构振型连续、多样,抗倒塌储备大,抗震能力强,M3、M4曲线末端对应的Sa范围小,说明结构以低振型为主;“返折”曲线的存在说明在相应地震动下结构的稳定性差。综上所述,M1的抗震能力最好,其次为M3。各图中的一系列(DM,IM)点也为结构地震易损性分析奠定了数据基础。
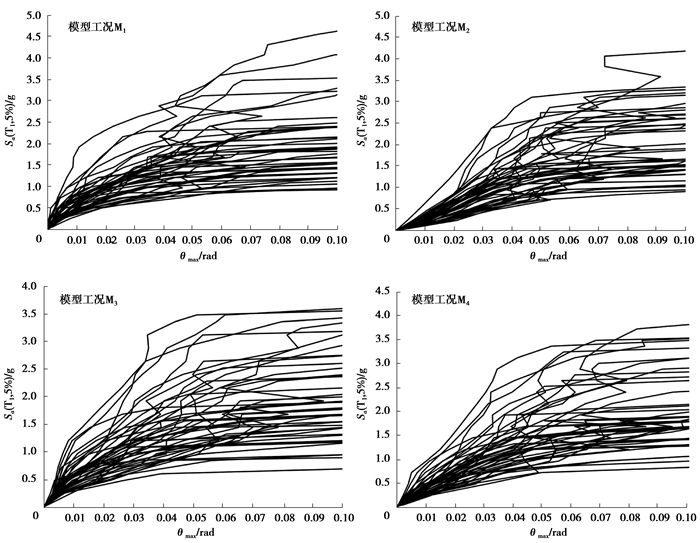
|
图 7 各模型的IDA曲线 Figure 7 IDA curves of each model |
中国规范采用“三水准,两阶段”抗震设防理论,规定第二阶段的层间位移角不应超过1/50,以使建筑物在大震下不致倒塌或防止发生危及生命的严重破坏。FEMA356[21]定义了结构的3个性能点:立即使用IO(immediate occupancy)、生命安全LS(life safe)和防止倒塌CP(collapse prevention),与之对应的层间位移角θmax依次为1%、2%和4%。因此,要满足中国“第二阶段”的抗震性能要求,则需要满足FEMA356中结构在大震下的LS(life safe)性能水准。地震易损性是指在不同地震动强度作用下结构发生各级破坏状态的概率,它在概率的意义上定量给出结构的抗震性能。通常认为结构在地震作用下的结构反应D符合对数正态分布,即结构损伤指标DM(θmax)与地震动强度指标IM(Sa(T1, 5%))符合指数函数关系式,该关系式又称地震概率需求模型。结构能力函数C符合对数正态分布。假设结构在各性态点处的能力均值为θc,标准差为δc。HAZUS99(高标准耐震设计规范)建议将FEMA356各性态点结构能力参数的标准差δc取为0.38。由于结构反应函数D和结构能力函数C都服从对数正态分布,通过数学转换处理,得出了结构模型在不同级别地震下的超越概率函数公式,其中α、β是地震概率需求模型参数。
| ${P_{\rm{f}}} = \mathit{\Phi }\left( {\frac{{{L_{\rm{n}}}(\alpha {{({S_{\rm{a}}}({{\rm{T}}_1},5\% ))}^\beta }/{\theta _{\rm{c}}})}}{{0.4}}} \right)。$ | (7) |
根据IDA分析结果,对地震动强度值Sa(T1, 5%)和结构损伤参数θmax取对数,运用Matlab软件进行线性回归分析,得到各模型的地震概率需求模型,进而得出结构模型的易损性公式。将θc取生命安全LS(life safe)性态点的结构能力均值0.02,即可得到与中国抗震规范相对应的的倒塌易损性公式,将4种模型的倒塌易损性公式绘制成曲线,如图 8所示。
| $ \begin{array}{l} {P_f}({{\rm{M}}_1}) = \mathit{\Phi }\left( {\frac{{{L_n}(0.024{\rm{ }}6{{({S_a}({{\rm{T}}_1},5\% ))}^{1.622}}/0.02)}}{{0.4}}} \right)\\ {P_f}({{\rm{M}}_2}) = \mathit{\Phi }\left( {\frac{{{L_n}(0.038{\rm{ }}3{{({S_a}({{\rm{T}}_1},5\% ))}^{0.865}}/0.02)}}{{0.4}}} \right)\\ {P_f}({{\rm{M}}_3}) = \mathit{\Phi }\left( {\frac{{{L_n}(0.027{\rm{ }}2{{({S_a}({{\rm{T}}_1},5\% ))}^{1.266}}/0.02)}}{{0.4}}} \right)\\ {P_f}({{\rm{M}}_4}) = \mathit{\Phi }\left( {\frac{{{L_n}(0.030{\rm{ }}5{{({S_a}({{\rm{T}}_1},5\% ))}^{1.109{\rm{ }}8}}/0.02)}}{{0.4}}} \right) \end{array} $ |
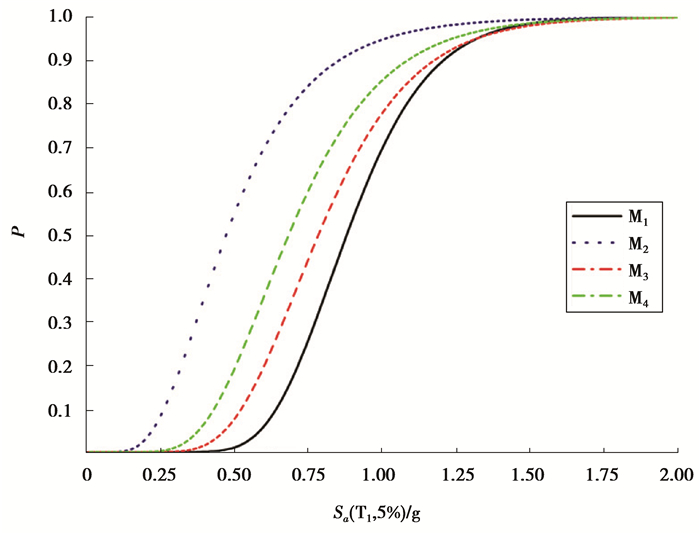
|
图 8 结构倒塌易损性曲线 Figure 8 The seismic fragility curves in the collapsed state |
运用OpenSees对各模型工况进行时程分析,得出M1~M4模型的第1周期T1(s)分别为0.760 5、1.407 840、0.937 78和0.838 11。根据结构第一周期和结构模型设计基本资料并参照中国抗震规范设计反应谱,可计算得出各模型在大震(罕见地震)下的地震动谱加速度值Sa(T1, 5%),进而可求得各模型工况在大震下的倒塌超越概率,具体计算数值如表 2所示。
| 表 2 设防大震下的倒塌超越概率 Table 2 The probability of collapse under strong earthquake |
ATC-63报告中建议:“在设防大震作用下结构倒塌概率小于10%,即可认为结构达到大震性能要求”。由表 2可知:模型M1、M2、M3、M4的倒塌超越概率依次为3.335%、20.053%、4.561%和20.805%,其中,模型M2、M4在大震下的超越概率均超过10%,根据ATC-63报告的建议,这2种模型工况不符合中国“大震不倒”的抗震性能要求。
4 结论基于OpenSees平台,验证了基于改进IMK恢复力模型的集中塑性铰模型的可行性。数值模型中梁柱单元采用集中塑性铰单元,其中,梁柱中部为反映其弹性属性的弹性单元(elastic element),梁柱两端作为破坏的集中部位,采用基于改进IMK恢复力模型的零长度弹簧单元(zeroLength element)。按规范设计了一种6层3跨框架结构,设计了填充墙的4种布置方式和与之对应的4种模型工况,对各模型工况进行了44条地震波记录的IDA分析和抗倒塌易损性分析,分析结果表明:M2和M4在设防大震下的倒塌超越概率均超过10%,根据ATC-63报告的建议,这2种类型的框架结构不符合规范中“大震不倒”的性能要求,建议在实际工程中尽量避免运用此类型框架结构,同时,对已有的此类结构进行加固处理。
| [1] |
刘光明, 杨红, 邹胜斌, 等.
基于新规范的钢筋混凝土框架抗震性能评价[J]. 重庆建筑大学学报, 2004, 26(1): 40–49.
LIU Guangming, YANG hong, ZOU Shengbin, et al. Seismic assessment of RC frame structure based on new design codes[J]. Journal of Chongqing jianzhu University, 2004, 26(1): 40–49. (in Chinese) |
| [2] |
施炜, 叶列平, 陆新征, 等.
不同抗震设防RC框架结构抗倒塌能力研究[J]. 工程力学, 2011, 28(3): 41–48.
SHI Wei, YE Lieping, LU Xinzheng, et al. Study on the collapse-resistant capacity of RC frames with different seismic fortification levels[J]. Engineering Mechanics, 2011, 28(3): 41–48. (in Chinese) |
| [3] |
潘毅, 杨琼, 林拥军, 等.
汶川地震中填充墙对钢筋混凝土框架结构抗震性能的影响及分析[J]. 四川建筑科学研究, 2010(5): 141–144.
PAN Yi, YANG Qiong, LIN Yongjun, et al. Seismic analysis of masonry-infilled RC frame structures in Wenchuan earthquake[J]. Sichuan Building Science, 2010(5): 141–144. (in Chinese) |
| [4] |
石宏彬.
框架结构填充墙影响和强梁弱柱成因研究[J]. 国际地震动态, 2013(3): 47–48.
SHI Hongbin. Study on infill wall function and strong beam-weak column damage for frame structures[J]. Recent Developments in World Seismology, 2013(3): 47–48. (in Chinese) |
| [5] |
叶列平, 陆新征.
汶川地震建筑震害分析[J]. 建筑结构学报, 2008, 29(04): 1–9.
YE Lieping, LU Xinzheng. Analysis on seismic damage of buildings in Wenchuan earthquake[J]. Journal of Building Structures, 2008, 29(04): 1–9. (in Chinese) |
| [6] | Ibarra L F, Medina R A, Krawinkler H. Hysteretic models that incorporate strength and stiffness deterioration[J]. Earthquake Engineering & Structural Dynamics, 2005, 34(12): 1489–1511. |
| [7] | Lignos D G, Krawinkler H. Development and utilization of structural component databases for performance-based earthquake engineering[J]. Journal of Structural Engineering, 2012, 139(8): 1382–1394. |
| [8] | Burton H, Deierlein G. Simulation of seismic collapse in nonductile reinforced concrete frame buildings with masonry infills[J]. Journal of Structural Engineering, 2013, 140(8): 1–10. |
| [9] | Haselton C B, Liel S, Taylor L, et al. Beam-column element model calibrated for predicting flexural response leading to global collapse of RC frame buildings[D]. California: PEER Report Pacific Engineering Research Center, 2008. |
| [10] | Panagiotakos T B, Fardis M N. Deformations of reinforced concrete members at yielding and ultimate[J]. Structural Journal, 2001, 98(2): 135–148. |
| [11] | Berry M, Parrish M, Eberhard M. PEER structural performance database user's manual (version 1.0)[M]. Berkeley: University of California, 2004. |
| [12] |
陆新征, 叶列平, 潘鹏, 等.
钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅰ:框架试验[J]. 建筑结构, 2012, 42(11): 19–22.
LU Xinzheng, YE Lieping, PAN Peng, et al. Pseudo-static collapse experiments and numerical prediction competition of RC frame structure Ⅰ:RC frame experiment[J]. Buildinng Structure, 2012, 42(11): 19–22. (in Chinese) |
| [13] |
黄群贤, 郭子雄, 朱雁茹, 等.
混凝土空心砌块填充墙RC框架抗震性能试验研究[J]. 建筑结构学报, 2012, 32(2): 110–118.
HUANG Qunxian, GUO Zixiong, ZHU Yanru, et al. Experimental study on seismic behavior of RC frames infilled with concrete hollow blocks[J]. Journal of Building Structures, 2012, 32(2): 110–118. (in Chinese) |
| [14] | Mahoney M, Hanson R D. Quantification of building seismic performance factors[D]. Washington D C: FEMA P695, 2009. |
| [15] | Estados Unidos Federal Emergency Management Agency. FEMA. Prestandard and commentary for the seismic rehabilitation of buildings[M]. Washington D C: FEMA, 2000. |
 2018, Vol. 41
2018, Vol. 41

