现阶段,中国城市车辆的快速发展,泊车问题越来越严重[1-2],如何合理、高效、方便地解决泊车问题,对于疏导交通拥堵及高效利用泊车位有着很大的意义。为了解决泊车难的问题,智能交通系统引入停车诱导系统。停车诱导系统关于泊车位的信息主要显示当前空余泊位信息,没有未来时刻的空余泊位情况[3]。而泊车位数量是动态变化的,这使得驾驶者看到诱导停车信息时的泊车位和实际到达泊车地点后的泊车位情况有较大的出入,造成诸多不便,因此采取合适方法对未来短时期内有效泊车位进行准确的预测显得相当重要。可见准确的实时空余泊位的预测是停车诱导系统的重要技术内容。
针对泊车位的预测问题,可建立的预测模型包括BP神经网络(BPNN, back propagation neural network)[4]模型,RBF(radial basis function)模糊神经网络模型[5-6]。RBF神经网络具有很好的函数逼近能力,但是它们只能在局部空间寻找最优解来确定网络结构参数,故在理论上很难求得网络结构等参数的最佳值。模糊神经网络是模糊理论同神经网络相结合的产物。它汇集了神经网络与模糊理论的优点,但在如何自动生成和调整隶属度函数和模糊规则,是一个棘手的问题。BP神经网络几乎可以逼近所有非线性函数,具有非常强大的自学能力,处理速度快,在预测方面应用也最为广泛[7],但是BP神经网络具有收敛速度慢,易出现震荡和陷入局部最小值等缺点[8]。文献[9]只是简单的通过改进学习速率和动量因子来提高BP神经网络的收敛速率,没有考虑到BP神经网络在阈值初始化的缺陷,并没起到较大优化模型的作用。研究采用遗传算法(GA, genetic algorithm)找到BP神经网络的最优权值和阈值,弥补传统BP神经网络随意选取初始值的缺陷。利用该算法对短期泊车位数量进行了预测分析,进一步提高了预测精度。
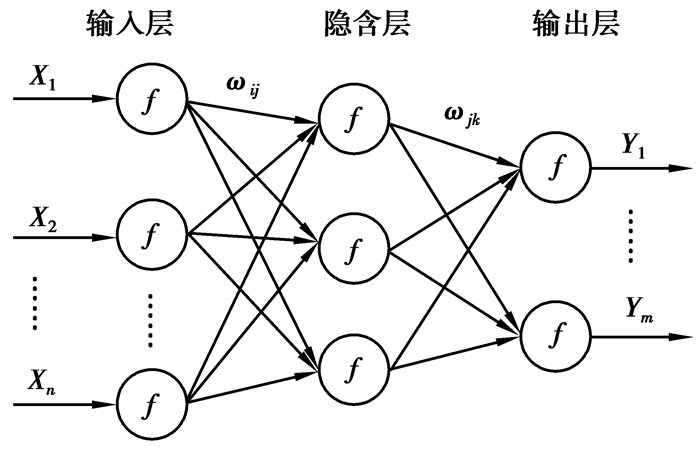
1 BP神经网络图 1是BP神经网络结构图,一共包括3层,信号通过输入层进入隐含层,在经过各神经元的信息处理后,经输出层输出。若未获得期望输出,则误差向后传递,调整权值和阈值,反复迭代,直至输出值接近期望值,误差控制在预设的范围内[10]。
|
图 1 BP网络的输入、输出示意图 Figure 1 The input and output schematic of BP network |
图 1中:x1, x2, …, xn为输入信号值;y1, y2, …, ym为信号输出值;w为网络的权值;f表示Sigmoid函数。
BP神经网络的预测过程:第一步,BP网络训练:输入层输入训练数据,初始化网络学习相应的参数,建立BP网络模型,接着训练BP网络,直到训练误差小于设置的最小误差要求时,网络训练结束。第二步,BP网络测试:取测试样本进行BP网络测试,如果测试结果达到网络泛化能力要求,则保存网络结构相应的的参数。否则,调整网络结构,重新进行训练。
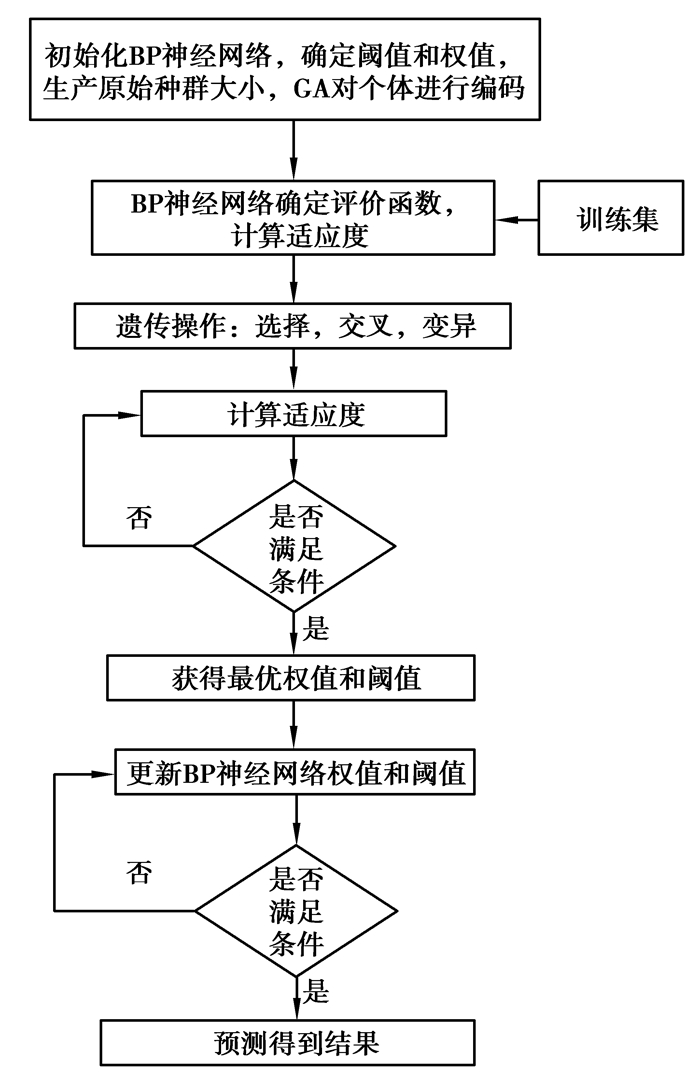
2 GA优化BP神经网络的空余车位预测算法 2.1 基本思路BP神经网络存在不足:第一,随机初始化网络的权值及阈值[11];第二,BP神经网络的收敛速度慢;第三,BP神经网络算法的梯度下降非凸问题,出现局部极小值是不可避免的。由于遗传算法具有全局优化搜索的特点[12],采用GA优化BP神经网络的方法,通过遗传算法的遗传算子选择、交叉和变异操作,对种群个体进行逐代择优,找到BP神经网络初始权值和阈值的最优解并进行赋值,然后对BP神经网络模型进行训练,最终获得全局最优预测值。GA优化BP神经网络的流程图 2所示。下面介绍具体操作。
|
图 2 GA优化BP神经网络流程图 Figure 2 The flowchart of BP network optimized by GA |
算法基本步骤如下
步骤1:设定种群大小。种群中个体数为P,初始化数据范围,随机生成原始种群W=(W1; W2;…; Wp)T,利用线性插值函数来生成个体Wi,采用Wi的实数向量W1,W2,…,Ws作为算法的一个染色体,采取实数编码方法。
步骤2:确定个体的评价函数。给BP神经网络的阈值和权值使用步骤1中得到的染色体进行赋值,然后输入训练样本,开始训练网络,达到预设的精度要求后停止训练,最后获得网络训练输出值。种群W中个体Wi的适应度由训练误差平方和来表示。
步骤3:采用轮盘赌法。选择概率为
| $ {p_i} = {f_i}/\sum\limits_{i = 1}^P {{f_i}, } \;i = 1, 2, \cdots, p, $ | (1) |
其中:fi为适应度值倒数,p为种群规模。
步骤4:采用实数交叉法。基因Wq在j位的交叉操作和基因Ws在j位的交叉操作如下
| $ \begin{array}{l} {\mathit{\boldsymbol{W}}_{qj}} = {\mathit{\boldsymbol{W}}_{qj}}\left( {1 - b} \right) + {\mathit{\boldsymbol{W}}_{sj}}b, \\ {\mathit{\boldsymbol{W}}_{sj}} = {\mathit{\boldsymbol{W}}_{sj}}\left( {1 - b} \right) + {\mathit{\boldsymbol{W}}_{qj}}b, \end{array} $ | (2) |
其中b是[0, 1]间的随机数。
步骤5:变异操作。第i个个体的第j个基因的变异操作如下
| $ {\mathit{\boldsymbol{W}}_{ij}} = \left\{ \begin{array}{l} \mathit{\boldsymbol{W}}{_{ij}} + ({\mathit{\boldsymbol{W}}_{ij}} - {\mathit{\boldsymbol{W}}_{{\rm{max}}}})f\left( g \right), r \ge 0.5, \\ {\mathit{\boldsymbol{W}}_{ij}} + ({\mathit{\boldsymbol{W}}_{{\rm{min}}}} - {\mathit{\boldsymbol{W}}_{ij}})f\left( g \right), r < 0.5, \end{array} \right. $ | (3) |
| $f\left( g \right) = {r_2}(1 - g/{G_{{\rm{max}}}}), $ | (4) |
其中:Wmax是最大值;Wmin为最小值;Gmax为进化次数最大值;g是迭代次数;r是位于[0, 1]间的随机数;r2是随机数。
步骤6:获得GA的最优个体,即BP神经网络预测模型的初始权值和阈值的最优值,训练模型,最终输出最优解。
3 仿真实验 3.1 实验环境实验利用Matlab R2015a,利用该环境下的工具箱构建模型。算法程序用Matlab语言编写。实验的误差评价体系采用平均相对误差(MRE),均方误差(MSE),平均绝对误差(MAE)[13]。即
| $ {\rm{MAE}} = \frac{1}{{{N_p}}}\sum\limits_{i = 1}^{{N_p}} {\left| {{x_i} - {{\hat x}_i}} \right|}, $ | (5) |
| $ {\rm{MRE}} = \frac{{\sum\limits_{i = 1}^{{N_p}} {{{\left( {{x_i} - {{\hat x}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^{{N_p}} {{{\left( {{x_i}} \right)}^2}} }}, $ | (6) |
| $ {\rm{MSE}} = \frac{1}{{{N_p}}}\sum\limits_{i = 1}^{{N_p}} {{{\left( {{x_i} - {{\hat x}_i}} \right)}^2}}, $ | (7) |
其中: xi为实际值,
BP神经网络使用n-2n+1-1经典3层结构[14],其参数设置如表 1。训练函数采用L-M优化算法trainlm,传递函数使用线性purelin函数和对数型logsig函数。GA的参数设置如表 2。
| 表 1 BP神经网络参数设置 Table 1 Parameters setting of BP naural netunrk |
| 表 2 GA参数设置 Table 2 Parameters setting of GA |
影响有效停车空余泊位变化的因素有很多,如季节、天气、节假日以及停车场周围车流量等,但是由于这些因素难以量化[16],并且考虑到车位的变化在时间上是渐进的过程,其变化一定具有规律性的特点。历史的停车数据基本上蕴含了该停车场的停车规律,所以考虑利用已有的停车场车位数的历史统计数据来构造对未来短期有效空余泊位数预测模型。这种研究方法是对历史数据潜在的变化规律的一种探索,从属于对时间序列分析的范畴。
以成都某地下停车场为例,对有效泊车位数的变化数据进行了预测分析。研究发现,智能停车场中某一时刻的泊车位数与前几个时刻的泊车位数有关,因此把停车场在t、t-5、t-10、t-15时刻的有效泊车位数作为网络的输入,输出节点是表示未来5 min的有效泊车位数。实验数据是从成都市某商场地下停车场的系统接口获取。实验获取从2016年5月的7天观测时间为08:00—23:00,间隔5 min的数据,共产生1 355个数据。实验数据分为2部分,一部分是前1 255个作为实验训练数据,另一部分是剩下的100个作为实验测试数据。采用BP模型和GABP模型对有效泊车位数的变化数据进行了预测分析并对实验结果进行了对比分析。
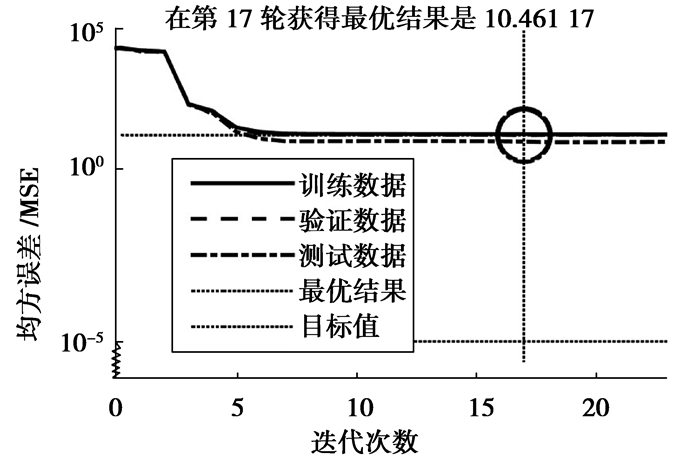
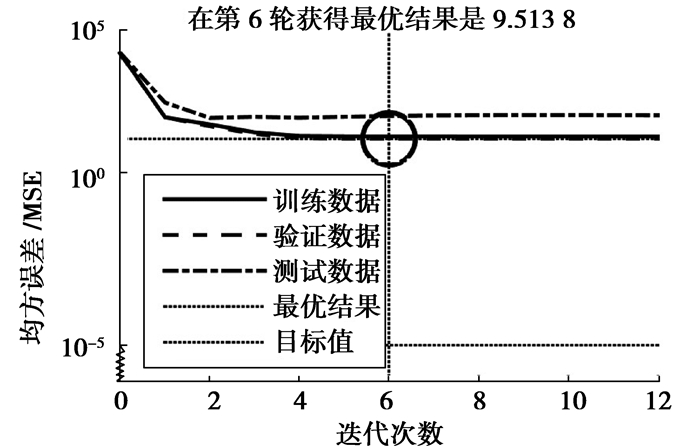
从图 2和图 3可以看出,BP模型需要18轮训练才能达到最好的网络结构,而GABP模型仅需要6轮训练就能得到最优解,使得网络快速收敛,避免出现发散现象。
|
图 3 BP网络训练 Figure 3 BP network training |
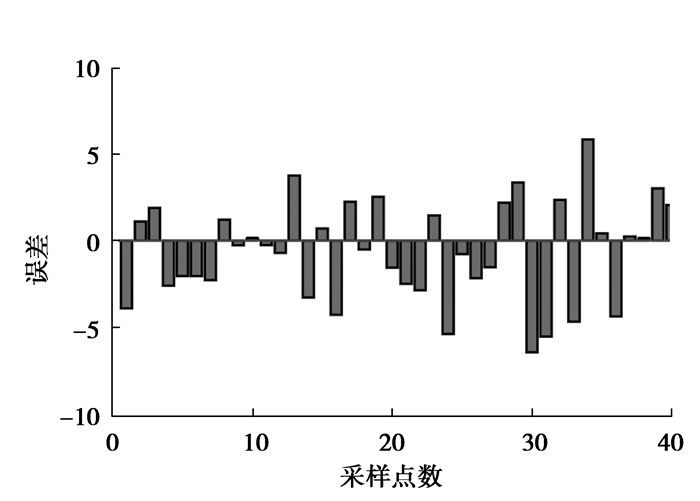
从图 4和图 6可以看出,虽然两种模型预测结果都能很好的反应泊车位数量的变化趋势,但是GA-BP模型更接近真实值,稳定性也更高。从图 5和图 7对比40个测试数据可以看出,传统BP算法模型个别时段的绝对误差比较大,其他时段相对误差均在10%左右,而GABP相对于传统BP相对误差减小,在6%左右。
|
图 4 GA-BP网络训练 Figure 4 GA-BP network training GA-BP网络训练 |

|
图 5 BP模型预测结果 Figure 5 The predicting results of BP |

|
图 6 BP神经网络误差图 Figure 6 The error figures of BP neural network |

|
图 7 GA-BP模型预测结果 Figure 7 The predicting results of GA-BP |
|
图 8 GA-BP误差图 Figure 8 The error figures of GA-BP |
表 3是GABP模型和BP模型在不同数量训练数据的情况下,100个预测数据误差体系中的3种误差值。从表 3中可以看出,GABP模型训练样本数量变化对精度影响不大,且训练样本越来越少的时候,GABP模型的预测精度的优越性约显著。这对小数据量样本短期预测来说尤为重要。
| 表 3 不同训练样本预测误差 Table 3 Prediction error of different training samples |
虽然GABP预测模型稳定性增强,预测精度也提高许多,但是遗传算法迭代时间很长,导致预测实时性较差,笔者将进一步研究新的方法以改善系统的实时跟踪性能。
4 结论研究提出改进后的模型利用GA遗传算子的相关操作,找到BP神经网络权值和阈值的最优值,并对该模型进行训练,最终获得全局最优预测值。最后,通过对成都某商场的地下停车场的泊车数据进行了验证分析。实验结果表明,GABP模型有效地提高了BP神经网络稳定性,避免陷入局部最小值,从而提高了有效泊车位的短期预测精度,表现出更好的非线性拟合能力,为有效泊车位进一步研究奠定了基础。
| [1] | Guo Z. Does residential parking supply affect household car ownership-the case of New York city[J]. Journal of Transport Geography, 2013, 26: 18–28. DOI:10.1016/j.jtrangeo.2012.08.006 |
| [2] | Syed Adnan S A A, Kadar Hamsa A A, et al. Factors influencing the parking demand of the park and ride facility at putrajaya public transportation terminal[J]. Journal of the Eastern Asia Society for Transportation Studies, 2015, 11: 78–81. |
| [3] |
赵崧淞. 区域泊车诱导系统诱导标志布局及设计[D]. 北京: 北京交通大学, 2014. ZHAO Songsong. Layout and design of parking guidance signs of regional parking guidance information system[D]. Beijing: Beijing Jiaotong University, 2014. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10004-1014152371.htm |
| [4] |
徐戊矫, 李武华, 王玉松, 等.
基于BP神经网络和SQP算法的轮毂锻模优化设计[J]. 重庆大学学报:自然科学版, 2014, 37(3): 16–22.
XU Wujiao, LI Wuhua, WANG Yusong, et al. BP neural network and SQP algorithm for the optimization of wheel die cavity[J]. Journal of Chongqing University:Natural Science Edition, 2014, 37(3): 16–22. (in Chinese) |
| [5] |
何伟. 模糊神经网络在交通流量预测中的应用研究[D]. 兰州: 兰州交通大学, 2012. HE Wei. Research on prediction of traffic flow using fuzzy neural networks[D]. Lanzhou: Lanzhou Jiaotong University, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10732-1012449437.htm |
| [6] |
彭显刚, 胡松峰, 吕大勇, 等.
基于RBF神经网络的短期负荷预测方法综述[J]. 电力系统保护与控制, 2011, 39(17): 144–148.
PENG Xiangang, HU Songfeng, LUE Dayong, et al. Review on grid short-term load forecasting methods based on RBF neural network[J]. Power System Protection and Control, 2011, 39(17): 144–148. (in Chinese) |
| [7] |
刘颖. 基于BP神经网络预测的城区占道停车智能管理系统的设计与实现[D]. 北京: 北京邮电大学, 2015. LIU Ying. Design and implement of city area parking intelligent management system based on BP neural network forecast[D]. Beijing: Beijing University of Posts and Telecommunications, 2015. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10013-1015583588.htm |
| [8] |
商林.
基于BP神经网络的PGIS空车位数预测建模研究[J]. 西部交通科技, 2010(7): 83–85.
SHANG Lin. Study on prediction modelling for pgis empty parking spot based on BP neutral network[J]. Western China, 2010(7): 83–85. (in Chinese) |
| [9] |
赵戊辰, 张玉茹.
BP神经网络用于停车场空余泊位的预测研究[J]. 哈尔滨商业大学学报:自然科学版, 2015(1): 44–46.
ZHAO Wuchen, ZAHNG Yuru. Application research of parking lot free parking number prediction based on back propagation neural network[J]. Journal of Harbin University of Commerce:Natural Sciences Edition, 2015(1): 44–46. (in Chinese) |
| [10] |
刘天舒. BP神经网络的改进研究及应用[D]. 哈尔滨: 东北农业大学, 2011. LIU Tianshu. The research and application on BP neural network[D]. Haerbin: Northeast Agricultural University, 2011. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10224-1011225712.htm |
| [11] | Yu F, Xu X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network[J]. Applied Energy, 2014, 134: 102–113. DOI:10.1016/j.apenergy.2014.07.104 |
| [12] | Grefenstette J J. Genetic Algorithms and their applications:proceedings of the second international conference on genetic algorithms[M]. UK: Psychology Press, 2013. |
| [13] | Leng Z, Gao J, Qin Y, et al. Short-term forecasting model of traffic flow based on GRNN[C]//2013 25th Chinese Control and Decision Conference (CCDC). [S. l. ]: IEEE, 2013: 3816-3820. |
| [14] | Wang L, Zeng Y, Chen T, et al. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting[J]. Expert Systems with Applications, 2015, 42(2): 855–863. DOI:10.1016/j.eswa.2014.08.018 |
| [15] |
曹智慧. 基于BP神经网络的空余泊位的短时预测和自动寻车系统的研究[D]. 广州: 华南理工大学, 2012. CAO Zhihui. Free parking spaces in short-term prediction based on BP neural network and automatic car locator system[D]. Guangzhou: South China University of Technology, 2011. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10561-1012451205.htm |
| [16] |
郭树明. 智能停车场管理系统中车位信息预测子系统的设计与实现[D]. 吉林: 吉林大学, 2012. GUO Shuming. Design and implementation of parking information forecasting subsystem in intelligent parking management system[D]. Jilin: Jilin University, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10183-1012371194.htm |
 2018, Vol. 41
2018, Vol. 41



