2. 武汉大学 数学与统计学院, 武汉 430072
2. School of Mathematics and Statistics, Wuhan University, Wuhan 430072, P. R. China
图像分割就是将图像区域聚类成不同性质的同质区域,它是由图像处理到图像分析的关键步骤。近年来,基于曲线演化和变分水平集的几何活动轮廓(GAC, geometric active contour model)模型,其较好的理论基础和分割效果得到了广泛关注。
GAC模型[1-3]基本思想是:首先将演化曲线隐含地表示为二元函数z=φ(x, y)的零水平集φ(x, y)=0,并建立耦合图像信息关于水平集函数φ的能量泛函。然后利用变分理论和梯度下降法得到水平集函数φ的发展方程,一般为偏微分方程。最后利用发展方程不断地更新水平集函数,从而驱动隐含其中的零水平集向目标物体的边界运行,发展方程的稳态解所对应的零水平集即为最终的分割结果。GAC模型最大的优点是能方便地在能量泛函中引入各种图像信息,并且能灵活地处理演化曲线拓扑结构的变化。
GAC模型主要分为基于边缘和基于区域的两类[4]。基于边缘的模型[5-6]利用图像梯度信息来识别目标边界,这类模型易受图像噪声的影响, 并且分割结果非常依赖于初始曲线的选择。基于区域的模型[7-9]利用不同性质区域之间统计信息的差异,驱动活动轮廓向同质区域之间的分界线上运动。这类模型具有较强的抗噪性,并且分割结果对初始曲线的选择不敏感。Chan和Vese基于MS泛函[10]提出一个无边缘活动轮廓模型[11](CV, Chan-Vese),该模型是一个非常著名的基于全局区域信息的几何活动轮廓模型,它利用活动轮廓内外区域的图像灰度均值差异驱动活动轮廓运动。后续很多专家学者根据不同的分割需求,基于CV模型提出了很多改进模型,例如为了分割灰度不均图像,Li等[9-12]提出了局部二值拟合(LBF, local binary fitting)模型;Vese等[13]为了进行多目标物体的分割,提出了多相水平集分割模型。Tang等[14]为了提高模型的抗噪性,提出了结合FCMS聚类的变分水平集模型,简称VFCMS模型。
CV模型基于图像全局信息,所以对噪声有一定鲁棒性。但是对于强噪声污染图像,CV模型并不能取得很好的分割效果。变分图像分解是一种新的图像处理技术,通过泛函极小化将图像f:Ω→R分解成f=u+v,其中u表示图像的结构分量,包含图像的主要特征,是图像f的简化逼近;v是图像的振荡成分或者是一个采样统计,一般包括纹理和噪声。笔者将BV-L2变分图像分解[15]和CV模型相结合,提出了一个新的变分图像分割模型,该模型利用BV-L2分解提取图像的结构分量,利用CV模型对结构分量进行分割,这样可以提高模型对噪声的鲁棒性,并且实现噪声图像的同时分割与去噪。
1 背景知识 1.1 BV-L2分解Rudin, Osher和Fatemi(ROF)[15]在1992年提出了著名的全变分(TV, total variation)极小化模型以进行图像去噪。他们采用TV(也称为BV半模)度量图像的结构分量u(即去噪图像);采用L2范数度量噪声。ROF模型的能量泛函定义为
| $ {E_1}\left( {u,f} \right) = \alpha {\left| u \right|_{{\rm{TV}}}} + \beta {\left\| {f - u} \right\|_{{L^2}}} = \alpha \int_\mathit{\Omega } {\left| {\nabla u} \right|{\rm{d}}x{\rm{d}}y} + \beta \int_\mathit{\Omega } {{{\left( {f - u} \right)}^2}{\rm{d}}x{\rm{d}}y} , $ | (1) |
其中,∇u表示图像函数u的弱梯度。极小化能量泛函(1),噪声图像f∈L2被分解为u+v,其中u∈BV表示去噪图像,v=f-u∈L2表示噪声分量,所以此模型也被称为BV-L2分解模型。此模型的优点有:1)能量泛函(1)是严格凸的,所以它存在唯一极小值点;2)函数u∈BV允许函数沿曲线出现间断,所以图像的边缘和轮廓可以在去噪图像u中得到很好的保持;3)u趋近于一个分片常值函数,所以模型具有很好的去除震荡(噪声)效果。正是因为具有这些优点,BV-L2分解模型到现在还是研究的热点,例如文献[16-18]。
1.2 CV模型Chan和Vese[11]基于MS(mumford shah)泛函提出了一个无边缘活动轮廓模型——CV模型,此模型归类为基于区域的图像分割模型。CV模型的基本思想是寻找一条闭合曲线C将图像区域划分为内部和外部区域,使得在内部与外部图像灰度平均值差最大,那么曲线C就可以看成是目标的轮廓。CV模型能量泛函定义为
| $ {E_2}\left( {{c_1},{c_2},\varphi } \right) = \mu \int_\mathit{\Omega } {\left| {\nabla H\left( \varphi \right)} \right|{\rm{d}}x{\rm{d}}y} + {\lambda _1}\int_\mathit{\Omega } {{{\left| {u - {c_1}} \right|}^2}H\left( \varphi \right){\rm{d}}x{\rm{d}}y} + {\lambda _2}\int_\mathit{\Omega } {{{\left| {u - {c_2}} \right|}^2}\\ \left( {1 - H\left( \varphi \right)} \right){\rm{d}}x{\rm{d}}y} 。$ | (2) |
利用变分法和梯度下降法,可得式(2)的梯度下降流为
| $ \frac{{\partial \varphi }}{{\partial t}} = \delta \left( \varphi \right)\mu {\rm{div}}\left( {\frac{{\nabla \varphi }}{{\left| {\nabla \varphi } \right|}}} \right) + \delta \left( \varphi \right)\left( {{\lambda _2}{{\left( {u - {c_2}} \right)}^2} - {\lambda _1}{{\left( {u - {c_1}} \right)}^2}} \right), $ |
其中c1和c2分别表示活动轮廓内部和外部区域的图像灰度均值,采用如下公式进行计算
| $ {c_1} = \frac{{\int_\mathit{\Omega } {u\left( {x,y} \right)H\left( {\varphi \left( {x,y} \right)} \right){\rm{d}}x{\rm{d}}y} }}{{\int_\mathit{\Omega } {H\left( {\varphi \left( {x,y} \right)} \right){\rm{d}}x{\rm{d}}y} }};{c_2} = \frac{{\int_\mathit{\Omega } {u\left( {x,y} \right)\left( {1 - H\left( {\varphi \left( {x,y} \right)} \right)} \right){\rm{d}}x{\rm{d}}y} }}{{\int_\mathit{\Omega } {\left( {1 - H\left( {\varphi \left( {x,y} \right)} \right)} \right){\rm{d}}x{\rm{d}}y} }}。$ | (3) |
由于CV模型采用了图像的全局信息,对噪声具有一定的鲁棒性。但是对于强噪声图像,CV模型会将部分对比度较大的噪声点作为目标提取出来,产生错误的分割。由于BV-L2分解模型具有很好的去噪效果,研究将其融合到CV模型,提出一个新的变分模型。此模型可以较好地分割噪声图像,并且作为副产品,模型还可以获得原噪声图像的一个去噪图像。为了叙述简便,简称此模型为ROF-CV模型。
2 研究模型 2.1 模型描述结合BV-L2分解和CV模型,笔者提出了一个新的变分模型以实现噪声图像的同时去噪和分割。模型定义如下
| $ \begin{array}{l} E\left( {u,\varphi ,{c_1},{c_2}} \right) = \alpha \int_\mathit{\Omega } {\left| {\nabla u} \right|{\rm{d}}x{\rm{d}}y} + \beta \int_\mathit{\Omega } {{{\left( {f - u} \right)}^2}{\rm{d}}x{\rm{d}}y} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\gamma \left( {\int_\mathit{\Omega } {{{\left( {u - {c_1}} \right)}^2}H\left( \varphi \right){\rm{d}}x{\rm{d}}y} + \int_\mathit{\Omega } {{{\left( {u - {c_2}} \right)}^2}\left( {1 - H\left( \varphi \right)} \right){\rm{d}}x{\rm{d}}y} } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mu \int_\mathit{\Omega } {\delta \left( \varphi \right)\left| {\nabla \varphi } \right|{\rm{d}}x{\rm{d}}y} , \end{array} $ |
其中,参数α, β, γ和μ是正的权重参数。
为了使得活动轮廓在演化过程中保持稳定,需要水平集函数在演化过程中保持为符号距离函数。所以在数值计算中,需要不断地重新初始化水平集函数为符号距离函数,这大大增加了计算的复杂度。Li等[19]在能量泛函中引入一个内部能量,定义为‖|∇φ|-1‖22,约束水平集函数在演化过程中保持为一个符号距离函数,第一个较好的解决了重新初始化这个难题。笔者将这个内部能量作为一个正则项引入到研究模型中。极小化此能量泛函的过程中,水平集函数φ将满足条件|∇φ|≈1,这说明水平集函数φ在演化过程中将近似保持为符号距离函数。
由于标准的Heaviside函数和Dirac函数在零点不可导,所以其在数值计算中很难进行处理。实验中采用正则化的Heaviside函数和Dirac函数,分别定义为
| $ {H_\varepsilon }\left( z \right) = \frac{1}{2}\left( {1 + \frac{2}{\pi} \arctan \left( {\frac{z}{\varepsilon }} \right)} \right);{\delta _\varepsilon }\left( z \right) = {{H'}_\varepsilon }\left( z \right) = \frac{1}{\pi} \cdot \frac{\varepsilon }{{{\varepsilon ^2} + {z^2}}}, $ |
当ε→0时,Hε(·)与δε(·)分别趋近于标准的Heaviside函数和Dirac函数。
采用上述2个策略对原能量泛函E(u, φ, c1, c2)进行改动,则最终的能量泛函定义为
| $ \begin{array}{l} E\left( {u,\varphi ,{c_1},{c_2}} \right) = \alpha \int_\mathit{\Omega } {\left| {\nabla u} \right|{\rm{d}}x{\rm{d}}y} + \beta \int_\mathit{\Omega } {{{\left( {f - u} \right)}^2}{\rm{d}}x{\rm{d}}y} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\gamma \left( {\int_\mathit{\Omega } {{{\left( {u - {c_1}} \right)}^2}{H_\varepsilon}\left( \varphi \right){\rm{d}}x{\rm{d}}y} + \int_\mathit{\Omega } {{{\left( {u - {c_2}} \right)}^2}\left( {1 - {H_\varepsilon }\left( \varphi \right)} \right){\rm{d}}x{\rm{d}}y} } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mu \int_\mathit{\Omega } {{\delta _{\rm{t}}}\left( \varphi \right)\left| {\nabla \varphi } \right|{\rm{d}}x{\rm{d}}y} + \frac{1}{2}\int_\mathit{\Omega } {{{\left( {\nabla \varphi - 1} \right)}^2}{\rm{d}}x{\rm{d}}y} 。\end{array} $ |
在能量泛函E(u, φ, c1, c2)中固定φ, c1, c2,求其关于u的极小值点。求E(u, φ, c1, c2)关于u的Gâteaux导数并令其等于零,得到E(u, φ, c1, c2)关于u取得极小值的必要条件—Euler-Lagrange方程
| $ - \alpha {\rm{div}}\left( {\frac{{\nabla u}}{{\left| {\nabla u} \right|}}} \right) - \beta \left( {f - u} \right) + \gamma \left( {\left( {u - {c_1}} \right){H_\varepsilon }\left( \varphi \right) + \left( {u - {c_2}} \right)\left( {1 - {H_\varepsilon }\left( \varphi \right)} \right)} \right) = 0。$ | (4) |
研究采用梯度下降法求解方程(4),其对应的梯度下降流方程为
| $ \frac{{\partial u}}{{\partial t}} = \alpha {\rm{div}}\left( {\frac{{\nabla u}}{{\left| {\nabla u} \right|}}} \right) + \beta \left( {f - u} \right) - \gamma \left( {\left( {u - {c_1}} \right){H_\varepsilon }\left( \varphi \right) + \left( {u - {c_2}} \right)\left( {1 - {H_\varepsilon }\left( \varphi \right)} \right)} \right)。$ | (5) |
初始条件为u(0, x, y)=f(x, y),边界条件为
在能量泛函中固定u, c1, c2,求能量泛函E(u, φ, c1, c2)关于水平集函数φ的极小值点。类似地,求能量泛函E(u, φ, c1, c2)关于φ的Gâteaux导数并令其等于零,得到Euler-Lagrange方程,采用梯度下降法得到发展方程
| $ \frac{{\partial \varphi }}{{\partial t}} = \gamma \delta \left( \varphi \right)\left( {{{\left( {u - {c_2}} \right)}^2} - {{\left( {u - {c_1}} \right)}^2}} \right) + \mu \delta \left( \varphi \right){\rm{div}}\left( {\frac{{\nabla \varphi }}{{\left| {\nabla \varphi } \right|}}} \right) + \left( {\Delta \varphi - {\rm{div}}\left( {\frac{{\nabla \varphi }}{{\left| {\nabla \varphi } \right|}}} \right)} \right)。$ | (6) |
在能量泛函中固定u, φ,求能量泛函E(u, φ, c1, c2)关于c1, c2的极小值点。分别求能量泛函E(u, φ, c1, c2)关于c1, c2导数并令其等于零,得到E(u, φ, c1, c2)关于c1, c2取得极小值的必要条件
| $ \int_\mathit{\Omega } {\left( {u - {c_1}} \right){H_\varepsilon }\left( \varphi \right){\rm{d}}x{\rm{d}}y} = 0;\int_\mathit{\Omega } {\left( {u - {c_1}} \right){H_\varepsilon }\left( \varphi \right){\rm{d}}x{\rm{d}}y} = 0。$ |
通过以上2个式子分别求c1和c2可得
| $ {c_1} = \frac{{\int_\mathit{\Omega } {u\left( {x,y} \right){H_\varepsilon }\left( {\varphi \left( {x,y} \right)} \right){\rm{d}}x{\rm{d}}y} }}{{\int_\mathit{\Omega } {{H_\varepsilon }\left( {\varphi \left( {x,y} \right)} \right){\rm{d}}x{\rm{d}}y} }}, $ | (7a) |
| $ {c_2} = \frac{{\int_\mathit{\Omega } {u\left( {x,y} \right)\left( {1 - {H_\varepsilon }\left( {\varphi \left( {x,y} \right)} \right)} \right){\rm{d}}x{\rm{d}}y} }}{{\int_\mathit{\Omega } {\left( {1 - {H_\varepsilon }\left( {\varphi \left( {x,y} \right)} \right)} \right){\rm{d}}x{\rm{d}}y} }}。$ | (7b) |
实际上c1和c2分别是活动轮廓内部和外部区域的图像灰度均值。
2.2 算法描述研究采用交替迭代算法求解模型。首先固定水平集函数φ和图像函数u,计算区域均值c1, c2;然后固定区域均值c1, c2和水平集函数φ,更新图像函数u;最后固定区域均值c1, c2和图像函数u,更新水平集函数φ,如此交替计算直至收敛。算法的停机准则:连续迭代T次的零水平集弧长L(φ=0)的改变量小于某个事先设定的阈值ξ,则停止迭代。事实上,如果相邻2次零水平集弧长的改变量L(φn+1=0)-L(φn=0)≤ξ第一次满足,活动轮廓也许并没有到达真正的目标边界,有可能只是放慢了演化速度或者到达局部极小。为了能够在一定程度上杜绝这种情况的发生,继续进行迭代,如果连续迭代T次的零水平集弧长的改变量小于事先设定的阈值ξ,则认为活动轮廓到达真正的目标边界。试验中,选择2个阈值参数分别为T=10和ξ=5,具体算法描述如下
步骤1 :初始水平集函数φn和图像函数un=f,令n=0,k=1。
步骤2 :利用式(7a)-式(7b)计算区域均值c1, c2。
步骤3 :利用偏微分方程(5)更新图像函数un+1。
步骤4 :利用偏微分方程(6)更新水平集函数φn+1。
步骤5 :如果L(φn+1=0)-L(φn=0)≤ξ,转向Step6,否则返回Step 2。
步骤6 :如果k=T,结束迭代,否则令k=k+1,返回Step2。
步骤7 :输出最后分割轮廓φn=0和分割二值图像c1H(φ)+c2(1-H(φ))。
3 实验结果及分析以不同噪声水平污染的人工图像和自然图像为实验对象验证ROF-CV模型的有效性:1)可以分割强噪声污染图像;2)可以同时获得去噪图像。并且和经典的CV模型和VFCMS模型进行了对比实验,显示模型在强噪声图像分割上的优势。为了对分割结果做量化评价,采用如下2个指标:Jaccard相似系数[20](JC, jaccard coefficient)和骰子相似系数[21](DSC, dice similarity coefficient),它们分别定义为
| $ JC = \frac{{N\left( {{S_1} \cap {S_2}} \right)}}{{N\left( {{S_1} \cup {S_2}} \right)}};{\rm{DSC}} = \frac{{2N\left( {{S_1} \cap {S_2}} \right)}}{{N\left( {{S_1}} \right) + N\left( {{S_2}} \right)}}, $ |
其中S1表示基准前景区域,S2表示采用分割模型找到的前景区域,N(S)表示区域S内像素点的个数。
3.1 参数选择对于初始水平集函数的选择,由于模型引入了约束水平集函数为符号距离函数的正则项,所以初始水平集函数的选择可以比较随意,研究在试验中选择为阶梯函数定义为
| $ {\varphi _0}\left( {x,y} \right) = \left\{ \begin{array}{l} 1,\left( {x,y} \right) \in {\rm{inside}}\left( C \right),\\ 0,\left( {x,y} \right) \in C,\\ - 1,\left( {x,y} \right) \in {\rm{outside}}\left( C \right), \end{array} \right. $ |
实验中参数的选择如下:参数α和β控制对图像进行平滑去噪的程度,为了不同试验中降低参数选择的难度,将参数α固定为α=1,去噪程度通过β控制:如果图像被低水平噪声污染,希望对其进行较弱的平滑,此时β取较大值;相反如果图像被高水平噪声污染,希望对其进行较强的平滑,此时β取较小值。所以参数β的取值要根据不同图像和不同的受噪声污染程度灵活地选取。
参数μ代表弧长项权重,控制活动轮廓的长度和光滑性。取值太小,分割结果中可能会出现伪边界和较小的孤立分割区域,取值太大,可能使得活动轮廓过度光滑而不能分割尖角型物体。为了在分割结果中较好地保持细节,同时分割尖角型物体,在所有试验中折中地选择μ=50。
正则化参数ε控制活动轮廓捕捉边界的范围,如果ε取值太小,捕捉范围小,此时活动轮廓有可能不能捕获离初始轮廓较远的边界。相反,如果ε取值太大,捕捉范围大,此时活动轮廓有“全局”的性质,则有可能不能捕获细节轮廓。为了能捕获离初始轮廓较远的边界,同时在分割结果中较好地保持细节,在所有试验中,笔者折中地选择ε=3。
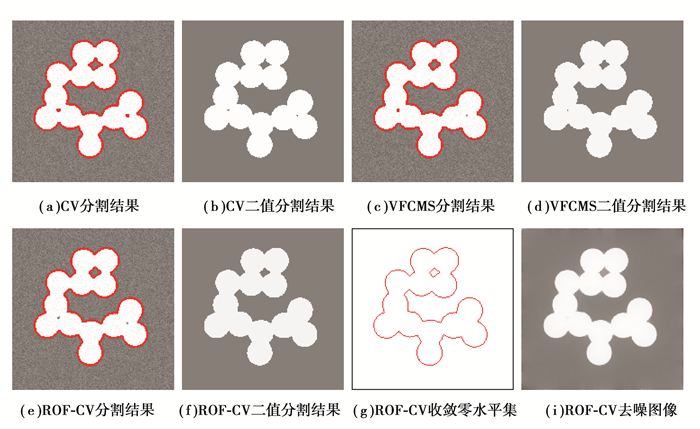
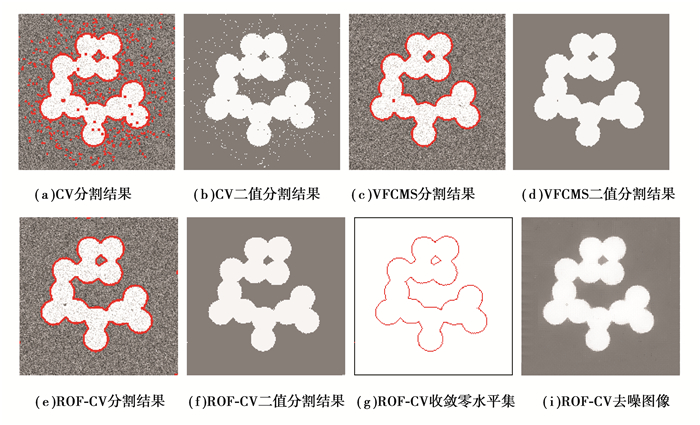
3.2 噪声人造图像分割图 1~图 3展示了CV模型,VFCMS模型和ROF-CV模型对3幅加入不同水平高斯噪声的人造图像的分割结果。初始轮廓选择为圆心在图像中心,半径为50的圆周。对于实验中参数β的取值,采用反复实验的方法进行选择,从β=1开始,以-0.05为步长,取βk=1-0.05 k反复进行实验,使得JC指标值第一次达到最大的βk值作为最优的参数值。实验中发现噪声强度越大,最优β取值越小。图 1~图 3实验中所取得的β值分别为0.85,0.70和0.55。
|
图 1 人造噪声图像的分割结果(噪声方差σ=10) Figure 1 The segmentation results of synthetic noisy image (noise variance σ=10) |
|
图 2 人造噪声图像的分割结果(噪声方差σ=30) Figure 2 The segmentation results of synthetic noisy image (noise variance σ=30) |

|
图 3 人造噪声图像的分割结果(噪声方差σ=50) Figure 3 The segmentation results of synthetic noisy image (noise variance σ=50) |
从实验结果可以看出,对于低噪声水平图像(例如σ=10,实验结果见图 1),3个模型在视觉上都取得较好的分割结果,并且通过JC与DSC指标量化比较(见表 1),仅仅利用图像全局信息的CV模型取得了比采用了平滑约束的VFCMS模型和ROF-CV模型更好的分割质量。但是随着噪声强度的增加(例如σ=30,实验结果见图 2),噪声的对比度变大,一部分噪声点的灰度值到达了目标物体灰度。此时CV模型将这一部分和目标灰度相近的噪声点也作为目标提取出来,出现了很多伪边界,而导致了错误的分割。VFCMS模型和ROF-CV模型由于采用了平滑约束,所以可以取得较好的分割效果。当图像被强噪声污染(例如σ=50,实验结果见图 3),由于结合了去噪能力很强的BV-L2分解,所以模型取得了比VFCMS模型和CV模型更优的分割质量。作为模型的副产品,还可以得到噪声图像的去噪恢复图像,分别见图 1到图 3的最后一幅图像。从实验结果可以看出,模型可以很好地去除噪声,得到视觉上较为满意的去噪结果。
表 2展示了图 1到图 3分割试验中,3个模型的计算CPU时间。通过时间比较可以看出,模型由于在CV模型中结合了BV-L2变分分解,所以计算复杂度要高于纯粹的CV模型,需要更多的运行时间。但是相对于结合模糊聚类算法的VFCMS模型,模型在计算速度上有较大优势。
3.3 噪声自然图像的分割图 4展示了2幅加入不同噪声水平的照相人图像(图中圆圈表示初始轮廓),图 4(a)和图 4(b)分别是加入了方差σ为30和50的高斯噪声的噪声图像。此自然图像相对于图 1—图 3中的人造图像包含了更多的复杂边界和细节,分割难度较大。以此人造图像为实验对象展示ROF-CV模型在分割噪声图像中去除噪声和同时保持细节的能力。

|
图 4 测试噪声照相人图像 Figure 4 Noisy "Cameraman" image |
图 5和图 6分别展示了图 4中2幅噪声照相人图像的分割结果。对于参数β的选择,直接采用噪声人造图像分割实验中参数β的选择数值,即加入方差σ=30高斯噪声,β选择为0.70;加入方差σ=50高斯噪声,β选择为0.55。从实验结果可以看出,CV模型受到噪声的影响,一部分孤立噪声点被当成目标被提取出来,使得分割结果中出现了大量的孤立区域,导致分割结果不准确,但是此模型具有较强的细节保持能力。VFCMS模型由于引入了图像的空间信息,相当于对分割结果进行了磨光,所以对噪声有一定鲁棒性。实验结果也显示了VFCMS模型可以在一定程度上排除噪声的影响得到较好的分割结果,并且细节轮廓也可以得到较好地保持。ROF-CV模型由于结合了去噪能力很强的BV-L2分解,所在这个3个分割模型中,对于噪声的鲁棒性最强。并且由于BV-L2分解可以较好的保持图像边缘和细节,所以模型也可以较好地分割图像的细节轮廓。

|
图 5 噪声照相人图像的分割结果(噪声方差σ=30) Figure 5 The segmentation results of noisy "Cameraman" image (noise variance σ=30) |

|
图 6 噪声照相人图像的分割结果(噪声方差σ=50) Figure 6 The segmentation results of noisy "Cameraman" image (noise variance σ=50) |
结合BV-L2变分分解和CV模型,提出了一个新的变分图像分割模型,该模型可以实现图像的同时分割和去噪。实验结果显示了模型对噪声图像分割的有效性和鲁棒性。并且和经典的CV模型与VFCMS模型相对,对于强噪声污染图像模型具有明显优势。但是模型也存在以下缺点:1)对于强噪声污染图像,在分割结果的同质区域会出现块状阶梯;2)模型只是一个二相分割模型,对于复杂图像不能取得好的分割效果。后续工作将集中在这2个问题的解决上。
| [1] |
刘瑞娟, 何传江, 原野, 等.
融合局部和全局图像信息的活动轮廓模型[J]. 计算机辅助设计与图形学学报, 2012, 24(03): 364–371.
LIU Ruijuan, HE Chuanjiang, YUAN Ye, et al. Active contours driven by local and global image fitting energy[J]. Journal of Computer-Aided Design & Computer Graphics, 2012, 24(03): 364–371. DOI:10.3969/j.issn.1003-9775.2012.03.012 (in Chinese) |
| [2] | Du X J, Cho D W, Bui T D. Image segmentation and inpainting using hierarchical level set and texture mapping[J]. Signal Processing, 2011, 91(4): 852–863. DOI:10.1016/j.sigpro.2010.09.002 |
| [3] | Estellers V, Zosso D, Lai R, S, et al. Efficient algorithm for level set method preserving distance function[J]. IEEE Transactions on Image Processing, 2012, 21(12): 4722–4734. DOI:10.1109/TIP.2012.2202674 |
| [4] | Xie X M, Wang C M, Zhang A J, et al. A robust level set method based on local statistical information for noisy image segmentation[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(9): 2199–2204. DOI:10.1016/j.ijleo.2013.10.026 |
| [5] | Caselles V, Kimmel R, Sapiro G, et al. Geodesic active contours[J]. International Journal of Computer Vision, 1997, 22(1): 61–79. DOI:10.1023/A:1007979827043 |
| [6] | Ning H, Ke L, Hong B. An improved geometric active contour model for concrete CT Image segmentation based on edge flow[J]. Chinese Journal of Electronics, 2010, 19(4): 387–390. |
| [7] | Liu S, Peng Y. A local region-based Chan-Vese model for image segmentation[J]. Pattern Recognition, 2012, 45(7): 2769–2779. DOI:10.1016/j.patcog.2011.11.019 |
| [8] | Zhang K H, Song H H, Zhang L, et al. Active contours driven by local image fitting energy[J]. Pattern Recognition, 2010, 4(43): 1199–1206. |
| [9] | Li C M, Kao C, Gore J, et al. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Transactions on Image Processing, 2008, 17(10): 1940–1949. DOI:10.1109/TIP.2008.2002304 |
| [10] | Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational problems[J]. Communications on Pure and Applied Mathematics, 1989, 42(5): 577–685. DOI:10.1002/(ISSN)1097-0312 |
| [11] | Chan T F, Vese L A. Active contours without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2): 266–277. DOI:10.1109/83.902291 |
| [12] | Locam K C. Implicit active contours driven by local binary fitting energy//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR). : IEEE Computer Society Press, 2007: 1-7. |
| [13] | Vese L A, Chan T F. A multiphase level set framework for image segmentation using the mumford and shah model[J]. International Journal of Computer Vision, 2002, 50(3): 271–293. DOI:10.1023/A:1020874308076 |
| [14] |
唐利明, 田学全, 黄大荣, 等.
结合FCMS与变分水平集的图像分割模型[J]. 自动化学报, 2014, 40(6): 1233–1248.
TANG Liming, TIAN Xuequan, HUANG Darong, et al. Image segmentation model combined with fcms and variational level set[J]. Acta Automatica Sinica, 2014, 40(6): 1233–1248. (in Chinese) |
| [15] | Rudin L I, Osher S, Fatemi E, et al. Nonlinear total variation based noise removal algorithms[J]. Physica D:Nonlinear Phenomena, 1992, 60(1): 259–268. |
| [16] | Chen F, Shen L, Xu Y, et al. The moreau envelope approach for the L1/TV image denoising model[J]. Inverse Problems and Imaging, 2014, 8(1): 53–77. DOI:10.3934/ipi |
| [17] | Duan Y, Huang W. A fixed-point augmented Lagrangian method for total variation minimization problems[J]. Journal of Visual Communication and Image Representation, 2013, 24(7): 1168–1181. DOI:10.1016/j.jvcir.2013.07.014 |
| [18] | Legarda S R, Brito L C, Espinosa R A, et al. Total variation regularization cost function for demodulating phase discontinuities[J]. Applied Optics, 2014, 53(11): 2297–2301. DOI:10.1364/AO.53.002297 |
| [19] | Li C M, Xu C Y, Gui C F, et al. Level set evolution without re-initialization: a new variational formulation//Proceedings of the 2005 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). : IEEE Computer Society Press, 2005: 430-436. |
| [20] | Zheng Q, Lu Z, Yang W, et al. A robust medical image segmentation method using KL distance and local neighborhood information[J]. Computers in Biology and Medicine, 2013, 43(5): 459–470. DOI:10.1016/j.compbiomed.2013.01.002 |
| [21] | Agrawal R, Sharma M. Review of segmentation methods for brain tissue with magnetic resonance images[J]. International Journal of Computer Network and Information Security (IJCNIS), 2014, 6(4): 55–62. DOI:10.5815/ijcnis |
 2018, Vol. 41
2018, Vol. 41

