2. 汽车噪声振动和安全技术国家重点实验室, 重庆 400039
2. State Key Laboratory of Vehicle NVH and Safety Technology, Chongqing 400039, P. R. China
振动系统中绝对振动位移的测量是振动主动控制[1-3]、系统辨识[4-6]等工程实践中的关键环节。车载光学平台、汽车悬架、无人机平台等振动平台的主动控制,需要实时准确的绝对状态(位移、速度)反馈才能获得良好的主动控制效果[7-9]。在振动系统中,通常用加速度计来测量绝对加速度信号,但很少有能方便、直接、准确测量绝对振动位移的传感器。在以前的研究工作中,很多学者用绝对加速度信号来估计或复原绝对位移信号,用这类方法复原的绝对位移信号往往存在低频带宽限制、积分初始值难以确定及延时等问题[10-11]。虽然有时候适当的延时有益于振动控制,但是通过积分滤波等方法得到的延时通常难以控制,且远大于主动控制需要的延时[12-14]。也有学者采用雷达或激光技术对绝对位移进行测量,但在传感系统的安装工艺和空间位置要求等方面存在很多问题[15-16]。
近几年,有学者采用准零刚度技术设计绝对振动位移传感系统,对微幅绝对振动位移进行直接、准确、实时的测量。Sun等[17-18]通过并联水平预压缩螺旋弹簧和竖直螺旋弹簧设计了绝对垂向振动位移传感系统,通过并联预压缩剪铰结构和竖直螺旋弹簧设计了三自由度平动绝对振动位移传感系统。然而,绝对垂向振动位移传感系统在使用过程中,水平弹簧一直处于压缩状态且有小幅的旋转运动,这给水平预压缩弹簧的安装带来了困难。妥吉英等[19]提出了一种带有凸轮滚珠装置的扭转准零刚度振动角度传感系统,可以对小幅扭转振动角位移进行直接测量。
笔者采用2根对称安装的欧拉压杆作为负刚度机构,提出了一种新型的准零刚度绝对振动位移传感系统。该传感系统在平衡位置附近具有很小的动刚度特性,在较宽频段上能对微幅绝对振动位移进行准确、实时的测量。
1 振动位移传感系统的工作机理如图 1所示,绝对位移传感系统由欧拉压杆、竖直螺旋弹簧、压力传感器、质量块和传感系统外壳组成。竖直弹簧的刚度为k, 上端与质量块相连,下端与压力传感器相连。压力传感器固定安装在传感系统外壳的底部中心。2根欧拉压杆对称地安装在质量块两侧,内端铰接在质量块上,外端铰接在传感系统外壳上。欧拉压杆两端均为铰接,易于安装。传感系统的安装初始位置如图 1(a)所示,竖直弹簧和欧拉压杆均处于自由状态,2根欧拉压杆向上倾斜,倾斜角为θ;传感系统的平衡位置如图 1(b)所示,2根欧拉压杆的4个端点处于同一水平线上,竖直弹簧处于压缩状态,压缩量为h。
|
图 1 绝对振动位移传感系统原理图 Figure 1 The schematic of absolute vibration displacement sensor system |
在绝对振动位移传感系统中,压缩的欧拉压杆提供负刚度,竖直螺旋弹簧提供正刚度。测量时需将竖直弹簧和质量块安装在被测对象的振动方向上,传感系统外壳直接与被测对象连接。质量块在平衡位置附近的绝对振动位移记为u,传感系统外壳的绝对振动位移记为z,z也即为被测对象的振动位移。当传感系统外壳与质量块有一个较小的相对位移y=u-z时,压力传感器的压力变化可表示为F=ky=k(u-z);当传感系统在平衡位置附近具有准零刚度特性时,质量块的振动响应u将远小于被测振动z,因此F≈-kz,即可用压力传感器的压力变化值来近似测量绝对振动位移。所以可以通过图 1所示的绝对振动位移传感系统来近似测量被测对象的绝对振动位移。
2 振动位移传感系统的静力学分析 2.1 欧拉压杆的静力学特性如图 2所示的两端铰支欧拉压杆结构,设在初始状态时,其中心点的横向变形为w=q0,当欧拉压杆发生的变形为小变形(w < 0.2L)时,其轴向载荷与轴向位移的关系可以近似表示为[20]
| $ P = {P_{\rm{e}}}\left\{ {1 - \frac{{{\rm{ \mathsf{ π} }}{q_0}}}{L}{{\left[ {{{\left( {\frac{{{\rm{ \mathsf{ π} }}{q_0}}}{L}} \right)}^2} + \frac{{4l}}{L}} \right]}^{ - 1/2}}} \right\}\left[ {1 + \frac{1}{8}{{\left( {\frac{{{\rm{ \mathsf{ π} }}{q_0}}}{L}} \right)}^2} + \frac{l}{{2L}}} \right], $ | (1) |

|
图 2 两端铰支欧拉压杆受力变形示意图 Figure 2 The compressed Euler beam with hinged-hinged boundary |
式中:Pe=EI(π/L)2为两端铰支欧拉压杆受轴向力时的临界屈服载荷;L为欧拉压杆长;l为欧拉压杆的轴向变形。
将2根欧拉压杆按照一定的倾斜角对称安装,组成传感系统的负刚度机构,如图 1(a)所示,此时2根欧拉压杆都处于自由状态,不考虑图中的竖直螺旋弹簧和质量块的质量。若在质量块上施加一个竖直向下的力F,记物块竖直向下的位移为x,则可得到2根欧拉压杆在竖直方向上的力与位移的关系为
| $ F = {P_{\rm{e}}}\left\{ {1 - \frac{{{\rm{ \mathsf{ π} }}{q_0}}}{L}{{\left[ {{{\left( {\frac{{{\rm{ \mathsf{ π} }}{q_0}}}{L}} \right)}^2} + 4\delta } \right]}^{ - 1/2}}} \right\}\left[ {2 + {{\left( {\frac{{{\rm{ \mathsf{ π} }}{q_0}}}{L}} \right)}^2} + \delta } \right] \\\times \frac{{\sqrt {1 - {\gamma ^2}} - \left( {x/L} \right)}}{{{{\left[ {{{\left( {x/L} \right)}^2} - \left( {2x/L} \right)\sqrt {1 - {\gamma ^2}} + 1} \right]}^{1/2}}}}, $ | (2) |
式中:
如图 1(b)所示,当2根欧拉压杆的4个端点在同一水平线上时,欧拉压杆产生的力均在水平方向上,且相互抵消,在竖直方向上的恢复力为零,称其为平衡位置。欧拉压杆在竖直方向上产生的恢复力是关于平衡位置对称的,所以将坐标原点在初始位置的位移x换成坐标原点在平衡位置的位移u(-h < u < h,
| $ u = x - L\sqrt {1 - {\gamma ^2}} 。$ | (3) |
将式(3)代入到式(2)中,并进行量纲一处理,可得负刚度机构的量纲一的力与位移的关系为
| $ \begin{array}{*{20}{c}} {{\hat F} = \left\{ {1 - {\rm{ \mathsf{ π} }}{{\hat q}_0}{{\left[ {{{\left( {{\rm{ \mathsf{ π} }}{{\hat q}_0}} \right)}^2} + 4\left( {1 - \hat \varepsilon } \right)} \right]}^{ - 1/2}}} \right\} \times }\\ {\left[ {\hat \varepsilon - {{\left( {\frac{{{\rm{ \mathsf{ π} }}{{\hat q}_0}}}{2}} \right)}^2} - 3} \right] \times \frac{{\hat u}}{{\hat \varepsilon }},} \end{array} $ | (4) |
式中:
将式(4)对
| $ \begin{array}{*{20}{c}} {\hat K = \frac{{2{\rm{ \mathsf{ π} }}{{\hat q}_0}{{\hat u}^2}\left[ {3 + {{\left( {\frac{{{\rm{ \mathsf{ π} }}{{\hat q}_0}}}{2}} \right)}^2} - \sqrt {{{\hat u}^2} + {\gamma ^2}} } \right]}}{{\left( {{{\hat u}^2} + {\gamma ^2}} \right){{\left[ {{{\left( {{\rm{ \mathsf{ π} }}{{\hat q}_0}} \right)}^2} + 4 - 4\sqrt {{{\hat u}^2} + {\gamma ^2}} } \right]}^{3/2}}}} + }\\ {\left\{ {1 - \frac{{{\gamma ^2}\left[ {3 + {{\left( {\frac{{{\rm{ \mathsf{ π} }}{{\hat q}_0}}}{2}} \right)}^2}} \right]}}{{{{\left( {{{\hat u}^2} + {\gamma ^2}} \right)}^{3/2}}}}} \right\}\left[ {1 - \frac{{{\rm{ \mathsf{ π} }}{{\hat q}_0}}}{{{{\left[ {{{\left( {{\rm{ \mathsf{ π} }}{{\hat q}_0}} \right)}^2} + 4 - 4\sqrt {{{\hat u}^2} + {\gamma ^2}} } \right]}^{1/2}}}}} \right]。} \end{array} $ | (5) |
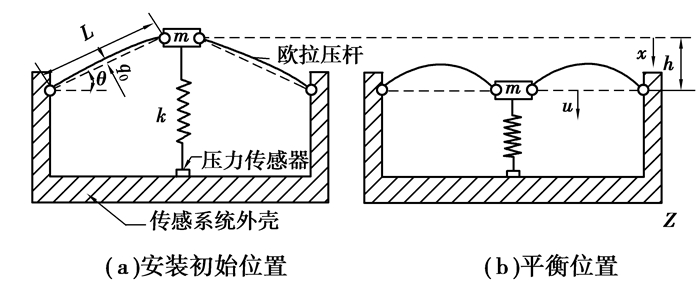
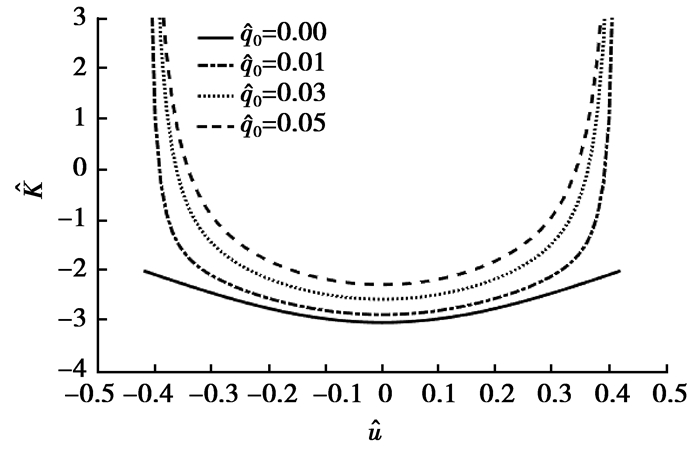
式(2)~(5)都只适用欧拉压杆的横向变形为小变形的情况,即w < 0.2L,可得欧拉压杆的初始安装倾角θ≈0°~26.6°。由式(5)可以得到负刚度机构在不同初始横向变形q0和不同初始安装倾角θ下量纲一的刚度与位移的关系如图 3和图 4所示。
|
图 3 不同初始横向变形时负刚度机构的量纲一的刚度曲线(初始安装倾斜角为25°) Figure 3 Non-dimensional stiffness curves of negative stiffness mechanism with different initial lateral deformation for θ=25° |
|
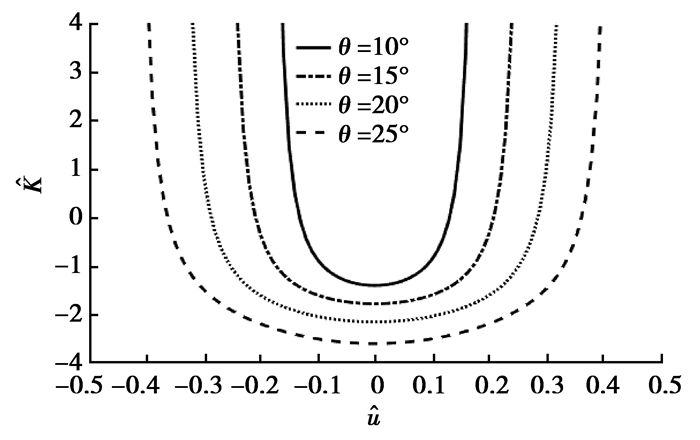
图 4 不同初始安装倾角时负刚度机构的量纲一的刚度位移曲线(初始横向变形为0.03)
Figure 4 Non-dimensional stiffness curves of negative stiffness mechanism with different initial installation angles for |
从图 3可以看出,当初始安装倾角一定时,欧拉压杆的初始横向变形越小,负刚度机构的最小刚度越小且负刚度区间越大。从图 4可以看出,当欧拉压杆的初始横向变形一定时,初始安装倾角越大,负刚度机构的最小刚度越小,负刚度区间就越大,欧拉压杆的初始安装倾角对负刚度系统的负刚度区间影响更显著。结合负刚度机构的刚度特性和欧拉压杆的特性,在之后的计算中,负刚度机构中欧拉压杆的初始横向变形为
将2根欧拉压杆组成的负刚度机构与刚度为k的线性螺旋弹簧并联,构造一种准零刚度振动位移传感系统,如图 1所示。用同样的方法可以得到传感系统的恢复力Fs、量纲一的恢复力
| $ {F_{\rm{s}}} = F + kx, $ | (6) |
| $ {{\hat F}_{\rm{s}}} = \lambda \cdot \hat F + \left( {\hat u + \sqrt {1 - {\gamma ^2}} } \right), $ | (7) |
| $ {{\hat K}_{\rm{s}}} = \lambda \cdot \hat K + 1, $ | (8) |
式中:
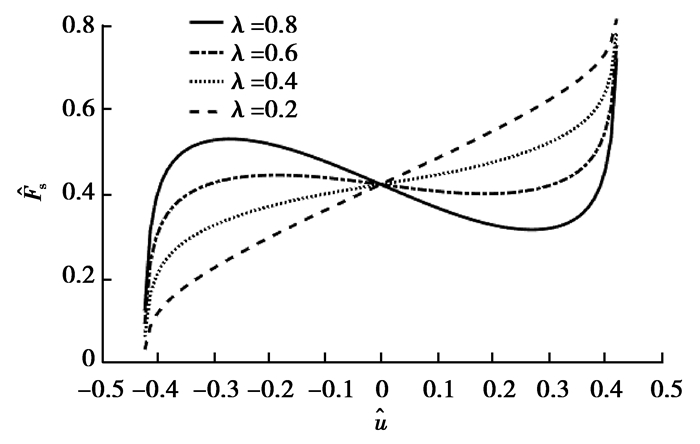
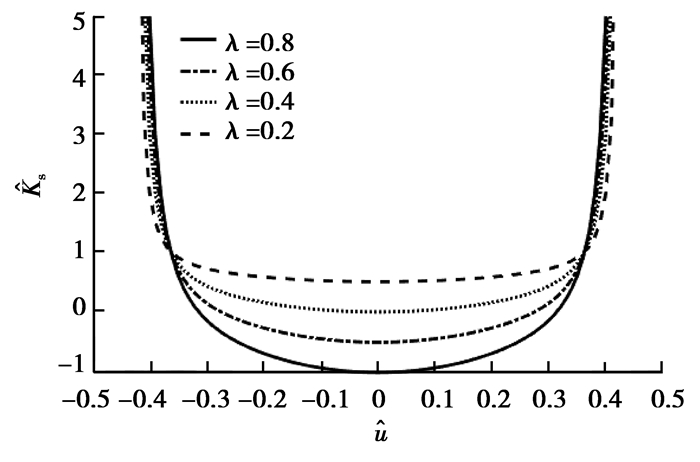
根据式(7)(8),可以得到不同λ值时,传感系统的量纲一的恢复力位移曲线和量纲一的刚度位移曲线如图 5、6所示。
|
图 5 不同刚度比时传感系统量纲一的力位移曲线 Figure 5 Non-dimensional force-displacement curves of sensor system with different stiffness ratio |
|
图 6 不同刚度比时传感系统量纲一的刚度曲线 Figure 6 Non-dimensional stiffness curves of sensor system with different stiffness ratio |
从图 5、6可以看出,当欧拉压杆的初始横向变形和初始安装倾角一定时,随着刚度比逐渐减小,传感系统在平衡位置即
| $ {\lambda _0} = - \frac{1}{{\left[ {1 - {\rm{ \mathsf{ π} }}{{\hat q}_0}/\sqrt {{{\left( {{\rm{ \mathsf{ π} }}{{\hat q}_0}} \right)}^2} + 4 - 4\gamma } } \right]\left\{ {1 - \left( {1/\gamma } \right)\left[ {3 + \frac{1}{4}{{\left( {{\rm{ \mathsf{ π} }}{{\hat q}_0}} \right)}^2}} \right]} \right\}}}。$ | (9) |
将式(9)代入到式(7)中,可以得到准零刚度传感系统的量纲一的恢复力位移表达式为
| $ {{\hat F}_{\rm{s}}} = {\lambda _0} \cdot \hat F + \left( {\hat u + \sqrt {1 - {\gamma ^2}} } \right)。$ | (10) |
为简化计算,采用泰勒公式将准零刚度传感系统的量纲一的恢复力在平衡位置处展开为三阶泰勒展开式
| $ {{\hat F}_{{\rm{st}}}} = \sqrt {1 - {\gamma ^2}} + \alpha {{\hat u}^3} + o\left( {{{\hat u}^5}} \right), $ | (11) |
式中
| $ \alpha = \frac{1}{{2{\gamma ^2}}} + \frac{2}{{\gamma \left[ {{{\left( {{\rm{ \mathsf{ π} }}{{\hat q}_0}} \right)}^2} - 4\gamma + 12} \right]}} + \frac{{{\rm{ \mathsf{ π} }}{{\hat q}_0}}}{{\gamma \left\{ {{{\left[ {{{\left( {{\rm{ \mathsf{ π} }}{{\hat q}_0}} \right)}^2} - 4\gamma + 4} \right]}^{3/2}} - {\rm{ \mathsf{ π} }}{{\hat q}_0}\left[ {{{\left( {{\rm{ \mathsf{ π} }}{{\hat q}_0}} \right)}^2} - 4\gamma + 4} \right]} \right\}}}。$ | (12) |
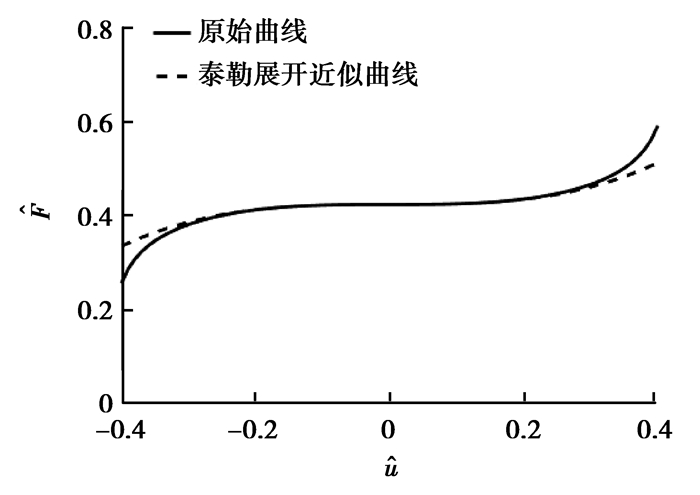
通过式(10)(11)可以得到原始的力位移曲线和用泰勒展开的近似力位移曲线,如图 7所示。由图 7可以看出,在平衡位置附近的大部分区域(占总区域的70%以上),泰勒展开的近似值都与原始值非常接近。因为传感系统测量的是小幅振动位移,质量块在平衡点附近振动的幅度也很小,所以用三阶泰勒展开式来代替原始精确表达式进行计算是可行的。
|
图 7 准零刚度系统的量纲一的力位移原始曲线与泰勒展开近似曲线对比 Figure 7 The comparison between the original curve and the Taylor expansion approximation curve of non-dimensional force-displacement of quasi-zero-stiffness system |
设图 1中的质量块的质量为m,且系统恰好在零刚度点达到平衡。平衡时2根欧拉压杆端点都在同一水平线上,质量块仅由竖直弹簧支撑。所以振动位移传感系统的静态方程为
| $ kL\sqrt {1 - {\gamma ^2}} - mg = 0。$ | (13) |
由于弹簧和欧拉压杆内部都存在阻尼,设系统的等效阻尼为线粘性阻尼,大小为c。在传感系统的外壳上施加一个竖直方向的小幅位移激励z=Z0cos ωt。利用牛顿第二定律,可得传感系统的运动方程为
| $ mg - kL\left[ {\alpha {{\left( {\hat u - \hat z} \right)}^3} + \sqrt {1 - {\gamma ^2}} } \right] - c\frac{{{\rm{d}}\left( {u - z} \right)}}{{{\rm{d}}t}} = m\frac{{{{\rm{d}}^2}u}}{{{\rm{d}}{t^2}}}, $ | (14) |
式中
| $ m\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} + c\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + kL\left( {\alpha {{\hat y}^3} + \sqrt {1 - {\gamma ^2}} } \right) - mg = m{\omega ^2}{Z_0}\cos \omega t, $ | (15) |
式中
| $ \frac{{{{\rm{d}}^2}\hat y}}{{{\rm{d}}{\tau ^2}}} + 2\xi \frac{{{\rm{d}}\hat y}}{{{\rm{d}}\tau }} + \alpha {{\hat y}^3} = {\mathit{\Omega }^2}{z_0}\cos \mathit{\Omega }\tau , $ | (16) |
式中:
采用谐波平衡法求解振动位移传感系统的动力学模型,得到稳态响应幅值与频率之间的近似关系。设传感系统的稳态响应为y=a cos ωt+b sin ωt,其量纲一表达式为
| $ \hat y = \hat a\cos \mathit{\Omega }\tau + \hat b\sin \mathit{\Omega }\tau , $ | (17) |
式中:
| $ \begin{array}{*{20}{c}} { - \hat a{\mathit{\Omega }^2}\cos \mathit{\Omega }\tau - \hat b{\mathit{\Omega }^2}\sin \mathit{\Omega }\tau + 2\xi \hat b\mathit{\Omega }\cos \mathit{\Omega }\tau - }\\ {2\xi \hat a\mathit{\Omega }\sin \mathit{\Omega }\tau + \frac{{\alpha {{\hat a}^3}}}{4}\left( {3\cos \mathit{\Omega }\tau + \cos 3\mathit{\Omega }\tau } \right) + }\\ {\frac{{\alpha {{\hat b}^3}}}{4}\left( {3\sin \mathit{\Omega }\tau - \sin 3\mathit{\Omega }\tau } \right) + \frac{{3\alpha {{\hat a}^2}\hat b}}{4}\left( {\sin \mathit{\Omega }\tau + \sin 3\mathit{\Omega }\tau } \right) + }\\ {\frac{{3\alpha \hat a{{\hat b}^2}}}{4}\left( {\cos \mathit{\Omega }\tau + \cos 3\mathit{\Omega }\tau } \right) = {\mathit{\Omega }^2}{z_0}\cos \mathit{\Omega }\tau 。} \end{array} $ | (18) |
忽略其中的高次谐波项,令等式左右两边的一次谐波项的系数分别相等,则
| $ \left\{ \begin{array}{l} - \hat a{\mathit{\Omega }^2} + 2\xi \hat b\mathit{\Omega } + \frac{3}{4}\alpha {{\hat a}^3} + \frac{3}{4}\alpha \hat a{{\hat b}^2} = {z_0}{\mathit{\Omega }^2},\\ - \hat b{\mathit{\Omega }^2} - 2\xi \hat a\mathit{\Omega }+\frac{3}{4}\alpha {{\hat b}^3} + \frac{3}{4}\alpha {{\hat a}^2}\hat b = 0。\end{array} \right. $ | (19) |
振动位移传感系统的测量精度可以用测量值y与被测值z的稳态幅值比T和相位差Φ描述, T和Φ可以表示为
| $ T = \frac{{\left| y \right|}}{{{Z_0}}} = \frac{{\sqrt {{{\hat a}^2} + {{\hat b}^2}} }}{{{Z_0}}}, $ | (20) |
| $ \mathit{\Phi } = \arctan \frac{{\hat b}}{{\hat a}}。$ | (21) |
定义传感系统的幅值误差在5%以内,且相位偏差在5°以内,则认为传感系统能对被测振动进行有效测量,即
| $ \left\{ \begin{array}{l} \left| {T - 1} \right| \times 100\% \le 5\% ,\\ \left| \mathit{\Phi } \right| \le {5^ \circ }。\end{array} \right. $ | (22) |
取振动位移传感系统的结构参数如表 1所示。下面通过求解式(19)~(22),讨论等效阻尼c、刚度比λ和被测幅值Z0对传感系统测量精度的影响和传感系统的起始测量频率。传感系统在不同参数条件下的起始测量频率在图中用星号(*)标出。
| 表 1 准零刚度振动位移传感系统结构参数表 Table 1 Structural parameters of quasi-zero-stiffness vibration displacement sensor system |
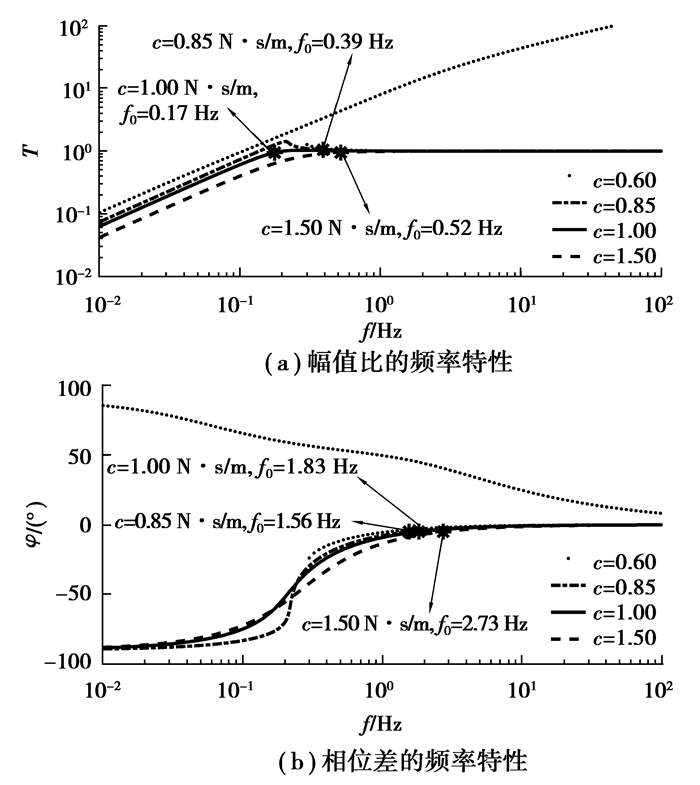
图 8为不同等效阻尼下传感系统的测量效果对比图。当等效阻尼过小(如c≤0.60 N·s/m)时,传感系统会在很宽频段上出现跳频现象,导致传感系统无法进行测量;适当增大等效阻尼可以有效抑制共振峰附近的幅值误差,缩小或消除跳频现象出现的频段,但会稍微增加相位误差;当等效阻尼过大(如c≥1.50 N·s/m)时,传感系统在低频段的幅值误差略有增大,相位误差明显增大。如图 8所示,不同阻尼下,传感系统满足幅值精度要求的频率非常低(0.60 Hz以内),但满足相位精度要求的频率较高(1.50 Hz以上),所以传感系统的起始测量频率主要由相位误差决定。当c=0.85 N·s/m时,传感系统的起始测量频率为1.56 Hz。
|
图 8 传感系统在不同等效阻尼时频率特性图 Figure 8 Frequency characteristic diagram of sensor system with different equivalent damping |
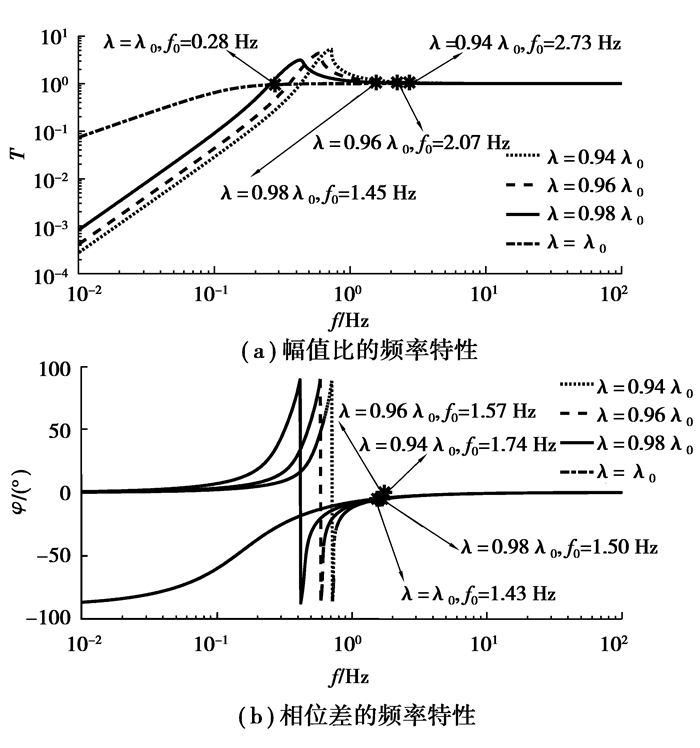
刚度比对共振峰附近的测量精度有很大的影响,如图 9所示。当刚度比从满足准零刚度条件的刚度比值逐渐减小时,传感系统能满足幅值精度要求的起始频率明显增加,对满足相位精度要求的起始频率影响很小且都在1.50 Hz左右。当刚度比满足准零刚度条件时,传感系统的起始测量频率为1.43 Hz。由式(8)和图 6可知,当刚度比大于满足准零刚度条件的刚度比值时,传感系统存在不稳定的负刚度区间,导致传感系统无法进行测量。
|
图 9 传感系统在不同刚度比时频率特性图 Figure 9 Frequency characteristic diagram of sensor system with different stiffness ratio |
从图 10发现,传感系统只能测量振动幅值Z0≤0.005 0 m的振动位移。当测量幅值Z0>0.005 0 m时,传感系统处于不稳定状态,不能进行测量。在可测量振动幅值范围内,被测振动幅值对传感系统满足幅值精度要求和相位精度要求的起始频率影响很小,传感系统的起始测量频率为1.54 Hz。
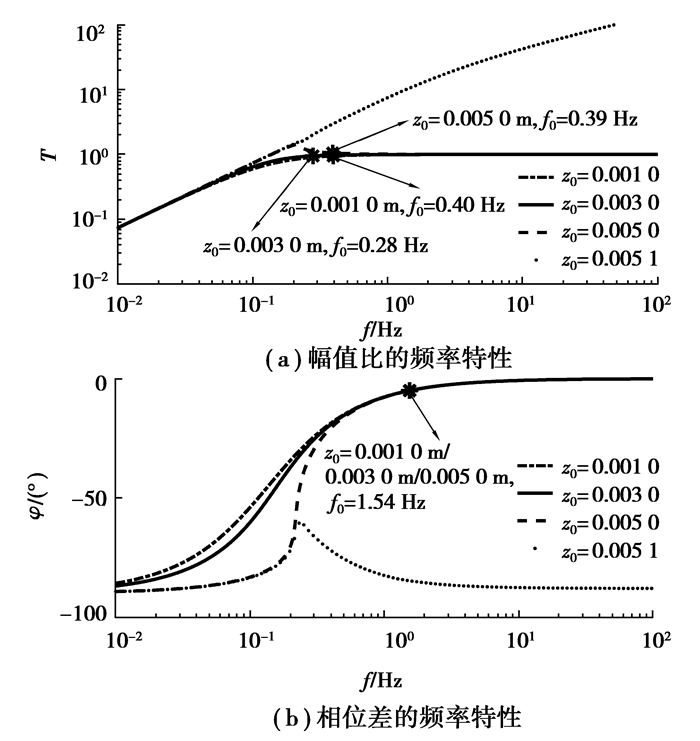
|
图 10 传感系统在不同测量幅值时频率特性图 Figure 10 Frequency characteristic diagram of sensor system with different amplitude of measured signal |
从图 8~10发现,不同的等效阻尼和刚度比主要影响传感系统的起始测量频率,且满足相位精度要求的起始频率较高,决定了传感系统的起始测量频率。在传感系统的可测量范围内,随着被测振动频率的增加,传感系统的测量精度越高,且受结构参数的影响越小。当选取合适的等效阻尼和刚度比时,传感系统的幅值测量范围为Z0≤0.005 0 m,适用频率范围为f≥1.60 Hz。
4.3 振动位移传感系统的时域测量效果根据上述分析,给出了一种传感系统结构参数方案如表 1所示。采用龙格库塔法求解传感系统的动力学模型,得到传感系统的时域响应信号-y。通过对比测量值-y和被测值z可以得到传感系统的时域测量效果。下面讨论被测信号为谐波信号、周期信号及随机信号时传感系统的测量效果。
当被测谐波信号为z=0.003sin(3.2πt+0.2π)时,传感系统的测量值与被测值之间的对比和测量值与被测值之间的误差如图 11所示。传感系统的测量值与被测值很接近,被测振动的峰值为0.003 00 m,测量误差的峰值约为0.000 15 m。因此,在谐波激励下,该新型振动位移传感系统的测量值-y可以近似代表绝对振动信号z。

|
图 11 传感系统在谐波激励下的测量值与被测振动的对比 Figure 11 The comparison between the measured value and original signal value under harmonic excitation |
当被测周期信号为z=0.001sin(3π+0.2π)+0.003sin(4π-0.3π)+0.005sin(8π-0.7π)时,传感系统的测量效果如图 12所示。传感系统的测量值与被测值非常接近,被测振动的峰值为0.008 50 m,测量误差的峰值约为0.000 32 m。因此,在周期激励下,该新型振动位移传感系统的测量值-y可以近似代表绝对振动信号z。
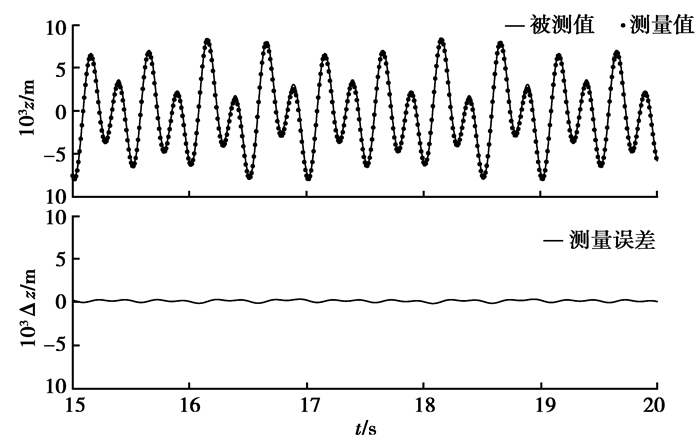
|
图 12 传感系统在周期激励下的测量值与被测振动的对比 Figure 12 The comparison between the measured value and original signal value under period excitation |
图 13中,被测随机振动信号z的均值为0,均方根值为0.000 85 m,频谱范围为1 Hz到10 Hz。传感系统的测量值与被测值非常接近,被测振动的峰值为0.004 10 m,测量误差的峰值约为0.000 16 m。因此,在随机激励下,该新型振动位移传感系统的测量值-y可以近似代表绝对振动信号z。

|
图 13 传感系统在随机激励下的测量值与被测振动的对比 Figure 13 The comparison between the measured value and original signal value under random excitation |
笔者设计了一种新型准零刚度振动位移传感系统。分析了等效阻尼、刚度比及测量幅值等参数对传感系统测量性能的影响和不同激励形式下的动态测量性能。理论分析和数值仿真结果表明,通过合理地设计传感系统的结构参数,该新型准零刚度传感系统可以直接对微幅振动位移进行准确、实时的测量。进一步的研究工作是加工传感系统样件进行实验验证。
| [1] | Le T D, Ahn K K. A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat[J]. Journal of Sound and Vibration, 2011, 330(26): 6311–6335. DOI:10.1016/j.jsv.2011.07.039 |
| [2] |
徐高楠, 黄海, 李伟鹏, 等.
空间挠性结构的Stewart平台主动基座振动控制[J]. 宇航学报, 2015, 36(4): 438–445.
XU Gaonan, HUANG Hai, LI Weipeng, et al. Active vibration control of space flexible structure using stewart platform as active base[J]. Journal of Astronautics, 2015, 36(4): 438–445. (in Chinese) |
| [3] |
张泉, 王瑞洲, 周丽平, 等.
柔性并联平台的动力学建模及主动振动控制[J]. 振动、测试与诊断, 2013, 33(6): 1025–1031.
ZHANG Quan, WANG Ruizhou, ZHOU Liping, et al. Dynamic modeling and active vibration control of flexible parallel platform[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(6): 1025–1031. (in Chinese) |
| [4] | Schon T B, Wills A, Ninness B. System identification of nonlinear state-space models[J]. Automatica, 2011, 47(1): 39–49. DOI:10.1016/j.automatica.2010.10.013 |
| [5] | Peeters M, Kerschen G, Golinval J C. Dynamic testing of nonlinear vibrating structures using nonlinear normal modes[J]. Journal of Sound and Vibration, 2011, 330(3): 486–509. DOI:10.1016/j.jsv.2010.08.028 |
| [6] | Yang Y, Peng Z K, Dong X J, et al. Nonlinear time-varying vibration system identification using parametric time-frequency transform with spline kernel[J]. Nonlinear Dynamics, 2016, 85(3): 1679–1694. DOI:10.1007/s11071-016-2786-1 |
| [7] | Benallegue A, Mokhtari A, Fridman L. Feedback linearization and high order sliding mode observer for a quadrotor UAV[C]//International Workshop on Variable Structure Systems, June 5-7, 2006, Alghero, Italy. [S. l. ]: IEEE, 2006: 365-372. |
| [8] | Xiao Z, Jing X. Frequency-Domain analysis and design of linear feedback of nonlinear systems and applications in vehiclesuspensions[J]. IEEE/ASME Transactions on Mechatronics, 2015, 21(1): 506–517. |
| [9] |
郑玲, 王宜, 谢熔炉.
主动约束层阻尼结构的振动控制[J]. 重庆大学学报, 2010, 33(2): 1–7.
ZHENG Ling, WANG Yi, XIE Ronglu. Vibration control of active constrained layer damping structure[J]. Journal of Chongqing University, 2010, 33(2): 1–7. (in Chinese) |
| [10] |
林腾蛟, 宋建军, 孟令宽, 等.
风机增速齿轮箱动力学性能优化方法[J]. 重庆大学学报, 2016, 39(4): 16–23.
LIN Tengjiao, SONG Jianjun, MENG Lingkuan, et al. A dynamic behavior optimization method of wind power speed-increase gearbox[J]. Journal of Chongqing University, 2016, 39(4): 16–23. DOI:10.11835/j.issn.1000-582X.2016.04.003 (in Chinese) |
| [11] |
张小龙, 潘登, 姜山, 等.
基于加速度的汽车悬架位移实时测试方法试验研究[J]. 农业机械学报, 2013, 44(10): 15–22.
ZHANG Xiaolong, PAN Deng, JIANG Shan, et al. Experiment on realtime test method for automotive suspension distance based on acceleration[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(10): 15–22. DOI:10.6041/j.issn.1000-1298.2013.10.003 (in Chinese) |
| [12] | Li H, Jing X, Karimi H R. Output-feedback-based control for vehicle suspension systems with control delay[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 436–446. DOI:10.1109/TIE.2013.2242418 |
| [13] | Zhao Y, Xu J. Effects of delayed feedback control on nonlinear vibration absorber system[J]. Journal of Sound and Vibration, 2007, 308(1-2): 212–230. DOI:10.1016/j.jsv.2007.07.041 |
| [14] | Sun X, Xu J, Fu J. The effect and design of time delay in feedback control for a nonlinear isolation system[J]. Mechanical Systems and Signal Processing, 2017, 87: 206–217. DOI:10.1016/j.ymssp.2016.10.022 |
| [15] |
毕运波, 涂国娇, 方伟, 等.
环形轨自动化制孔系统孔位修正方法[J]. 浙江大学学报(工学版), 2015, 49(10): 1863–1869.
BI Yunbo, TU Guojiao, FANG Wei, et al. Correcting method of hole position for flexible track automatic drilling system[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(10): 1863–1869. (in Chinese) |
| [16] |
毕运波, 李永超, 顾金伟, 等.
机器人自动化制孔系统[J]. 浙江大学学报(工学版), 2014, 48(8): 1427–1433.
BI Yunbo, LI Yongchao, GU Jinwei, et al. Robotic auto-matic drilling system[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(8): 1427–1433. (in Chinese) |
| [17] | Sun X, Jing X, Jian X, et al. A quasi-zero-stiffness-based sensor system in vibration measurement[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5606–5614. DOI:10.1109/TIE.2013.2297297 |
| [18] | Sun X, Jing X, Cheng L, et al. A 3-D quasi-zero-stiffness-based sensor system for absolute motion measurement and application in active vibration control[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(1): 254–262. DOI:10.1109/TMECH.2014.2338932 |
| [19] |
妥吉英, 邓兆祥, 张河山, 等.
新型扭转准零刚度的振动角度传感系统[J]. 西安交通大学学报, 2017, 51(8): 90–95.
TUO Jiying, DENG Zhaoxiang, ZHANG Heshan, et al. A new type of sensor system for angular vibration measurementof torsion quasizero-stiffness[J]. Journal of Xi'an Jiaotong University, 2017, 51(8): 90–95. DOI:10.7652/xjtuxb201708015 (in Chinese) |
| [20] | Liu X, Huang X, Hua H. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector[J]. Journal of Sound and Vibration, 2013, 332(14): 3359–3376. DOI:10.1016/j.jsv.2012.10.037 |
 2018, Vol. 41
2018, Vol. 41



