2. 重庆大学 自动化学院, 重庆 400044
2. School of Automation, Chongqing University, Chongqing 400044, P. R. China
双馈式感应电机已经广泛应用于并网的变速恒频风力发电系统中[1-2]。随着风力发电在供电体系中所占的比重快速增加,对双馈式风力发电机组的要求也越来越高。因此提高发电效率、减小负荷和降低机械效应,从而提高系统可靠性、延长使用寿命、降低发电成本成为研究的热点[3]。双馈式感应电机是一个多变量非线性系统,对其采用的控制方法主要分为两类:线性控制和非线性控制。然而,线性控制主要借助泰勒公式对系统的动态模型在特定的区域线性化,该方法仅有效作用于线性化区域,过于依赖系统的精确模型,且对参数变化、外界干扰的鲁棒性不强[3-4]。非线性控制主要有模糊控制[5]、神经网络控制[6]、反馈线性化控制[7]以及滑模控制[8]。滑模控制对系统参数变化和外界干扰鲁棒性强,相较于其他的非线性控制具有响应速度快、控制器易于工程实现,具有严格的稳定性等优点[8-9]。
抖振现象是滑模控制所固有的特性,抖振的大小与控制输入的幅值成正比,是阻碍滑模控制应用的主要原因[10]。传统的抑制抖振的方法主要采用高阶滑模控制、动态增益、趋近律等方法[11]。高阶滑模通常需要计算滑模变量的高阶导数,而二阶滑模中的Super-twisting算法,不需要滑模变量导数信息。但是该算法控制增益的精确确定需要干扰项可微且有具体界值,在实际控制中这个界值却很难准确获得[9-12]。故笔者选用自适应滑模控制,根据滑模变量的大小调节控制增益,以降低抖振。
笔者结合高阶滑模控制、自适应控制在抑制抖振现象中各自的优点,将自适应Super-twisting算法应用于风力发电系统中,不需要确定干扰项的准确界值即可确定控制增益。首先分析了风力发电系统以及双馈式感应电机在同步旋转坐标系下的降阶模型。接着将上述方法应用于双馈式发电机的变速恒频风力发电系统中,可通过调节风力发电机的转矩控制有功功率,实现低风速时最大风能捕获和高风速时额定功率运行。同时,根据电网功率因数需求调节定子侧无功功率,提高系统运行的动、静态性能。最后通过仿真验证了该可控制方案的可行性。
1 风机简介风机从风能中捕获的机械功率Pw以及风机获得的机械转矩Tw可以表示为[3-4]
| $ {P_{\rm{w}}} = \frac{1}{2}\rho {\rm{ \mathsf{ π} }}{R^2}{C_{\rm{p}}}\left( {\lambda ,\beta } \right){v^3}, $ | (1) |
| $ {T_{\rm{w}}}\left( {{\omega _{{\rm{rm}}}}} \right) = \frac{{{P_{\rm{w}}}}}{{{\omega _{{\rm{rm}}}}}} = \frac{{\rho {\rm{ \mathsf{ π} }}{R^5}{C_{\rm{p}}}\left( {\lambda ,\beta } \right)\omega _{{\rm{rm}}}^3}}{{2{\lambda ^3}}}, $ | (2) |
式中:ρ是空气密度;R是风机的叶片半径;v是风速;β是桨距角;ωrm是风机的转速;λ=ωrmR/v是叶尖速比;Cp(λ, β)是风能利用系数,与参数β、λ相关,可以表示为
| $ \left\{ \begin{array}{l} {C_{\rm{p}}}\left( {\lambda ,\beta } \right) = \frac{1}{2}\left( {\frac{{116}}{{{\lambda _1}}} - 0.4\beta - 5} \right){{\rm{e}}^{\left( { - \frac{{21}}{{{\lambda _1}}}} \right)}},\\ \frac{1}{{{\lambda _1}}} = \frac{1}{{\lambda + 0.08\beta }} - \frac{{0.035}}{{{\beta ^3} + 1}}。\end{array} \right. $ | (3) |
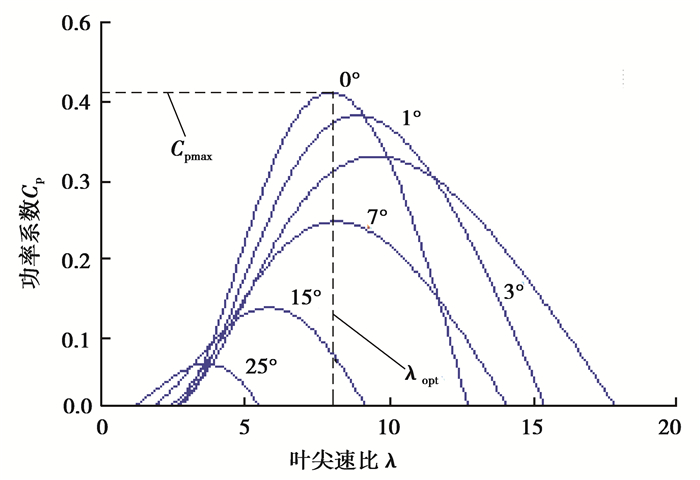
Cp(λ, β)的特性曲线如图 1所示,对于不同的β总存在唯一的λ使Cp取得极大值。当β=0,λopt=8.1时,Cp取得最大值Cpmax=0.41。
|
图 1 功率系数Cp(λ, β)曲线图 Figure 1 curves of wind power coefficient |
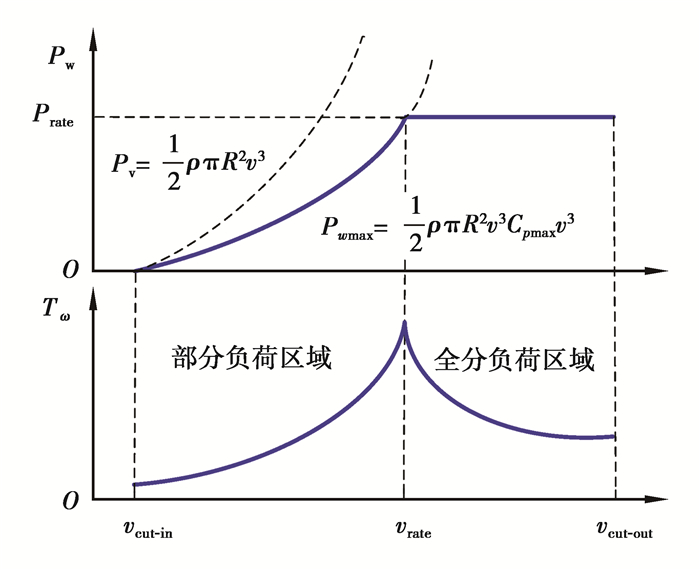
当风速达到切入风速vcut-in时,风机开始启动;当风速达到额定风速vrate,发电功率达到额定值;当风速达到切出速度vcut-out,风机停止运行[14]。不同风速区域的控制目标不同,如图 2所示。
|
图 2 有功功率分区域控制目标 Figure 2 the aim of active power in different zones |
为了分析的方便,可以将风机运行过程主要分为3部分。
1) 当风速在vcut-in与vrate区间时,即部分负荷区域,控制的目标是最大限度获得电能,即最大功率跟踪,此时通常保持β为零,使λ=λopt,则Cp=Cpmax。此时风机的机械转矩Topt与风机的转速相关,即
| $ {T_{{\rm{opt}}}}\left( {{\omega _{{\rm{rm}}}}} \right) = \frac{{\rho {\rm{ \mathsf{ π} }}{R^5}{C_{{\rm{pmax}}}}}}{{2\lambda _{{\rm{opt}}}^3}}\omega _{{\rm{rm}}}^2。$ | (4) |
2) 当风速在vrate与vcut-out区间时,即全负荷区域,控制的目标是保持从风中获得的功率为额定功率,可以通过调节β和λ来实现[8]。通过控制电磁转矩和桨距角调节Cp,进而控制功率。桨距系统可看作一阶惯性环节,且惯性系数为T,若风机获得功率为Pt,则桨距角的控制如图 3所示。

|
图 3 桨距角控制结构图 Figure 3 Control structure diagram of pitch angle |
此时风机机械转矩与额定功率和风机转速相关,即
| $ {T_{{\rm{opt}}}}\left( {{\omega _{{\rm{rm}}}}} \right) = \frac{{{P_{{\rm{rate}}}}}}{{{\omega _{{\rm{rm}}}}}}。$ | (5) |
3) 当风速达到vcut-out,为了风机免遭破坏需停止风机运行。
若忽略机组的阻尼系数、刚度系数,则风力发电机的简化轴动态运动方程可以表示为[13-14]
| $ {J_t}{{\dot \omega }_{{\rm{rm}}}} = {T_{\rm{w}}}\left( {{\omega _{{\rm{rm}}}}} \right) - {T_{\rm{g}}}, $ | (6) |
式中:Tg=kgTe是发电机电磁转矩在风机侧的等效值;Jt=Jr+kg2Jg是系统的总转动惯量。其中,kg是增速箱的增速比,Te是发电机的电磁转矩,Jr,Jg分别是风机与发电机的转动惯量。
为了使系统按照既定的目标稳定运行,根据公式(4)(5)可知发电机电磁转矩的参考值T*应当满足:
| $ {T^ * }\left( {{\omega _{{\rm{rm}}}}} \right) = \left\{ \begin{array}{l} \frac{{\rho {\rm{ \mathsf{ π} }}{R^5}{C_{{\rm{pmax}}}}}}{{2\lambda _{{\rm{opt}}}^3{k_{\rm{g}}}}}\omega _{{\rm{rm}}}^2,v \ge {v_{{\rm{rate}}}};\\ \frac{{{P_{{\rm{rate}}}}}}{{{\omega _{{\rm{rm}}}}{k_{\rm{g}}}}},{v_{{\rm{rate}}}} < v < {v_{{\rm{cut}}}};\\ 0,v > {v_{{\rm{rate}}}}。\end{array} \right. $ | (7) |
在两相同步旋转d,q坐标系下,双馈式感应发电机的定子和转子电压可以表示为[15]
| $ \left\{ \begin{array}{l} {u_{{\rm{s}}d}} = {{\dot \psi }_{{\rm{s}}d}} + {R_{\rm{s}}}{i_{{\rm{s}}d}} - {\omega _{\rm{s}}}{\psi _{{\rm{s}}q}},\\ {u_{{\rm{s}}q}} = {{\dot \psi }_{{\rm{s}}q}} + {R_{\rm{s}}}{i_{{\rm{s}}q}} + {\omega _{\rm{s}}}{\psi _{{\rm{s}}d}},\\ {u_{{\rm{r}}d}} = {{\dot \psi }_{{\rm{r}}d}} + {R_{\rm{r}}}{i_{{\rm{r}}d}} - \left( {{\omega _{\rm{s}}} - p{\omega _{\rm{r}}}} \right){\psi _{{\rm{r}}q}},\\ {u_{{\rm{r}}q}} = {{\dot \psi }_{{\rm{r}}q}} + {R_{\rm{r}}}{i_{{\rm{r}}q}} - \left( {{\omega _{\rm{s}}} - p{\omega _{\rm{r}}}} \right){\psi _{{\rm{r}}q}}。\end{array} \right. $ | (8) |
式中:ψsd,ψsq和ψrd,ψrq分别是定子磁链和转子磁链在d,q轴分量,满足
| $ \left\{ \begin{array}{l} {\psi _{{\rm{s}}d}} = {L_{\rm{s}}}{i_{{\rm{s}}d}} + {L_{\rm{m}}}{i_{{\rm{r}}d}},\\ {\psi _{{\rm{s}}q}} = {L_{\rm{s}}}{i_{{\rm{s}}q}} + {L_{\rm{m}}}{i_{{\rm{r}}q}},\\ {\psi _{{\rm{r}}d}} = {L_{\rm{r}}}{i_{{\rm{r}}d}} + {L_{\rm{m}}}{i_{{\rm{s}}d}},\\ {\psi _{{\rm{r}}q}} = {L_{\rm{r}}}{i_{{\rm{r}}q}} + {L_{\rm{m}}}{i_{{\rm{s}}q}}。\end{array} \right. $ | (9) |
其中,usd,usq和urd,urq(ird,irq,isd,isq)分别是定子和转子电压(电流)在d,q轴分量;Rs,Rr分别是定子电阻和转子电阻;ωs,ωr分别是网侧电压频率、电机转子角速度,p为电磁极对数,Ls,Lr和Lm分别是定子、转子自感和定子与转子绕组间的互感。
为了简化系统模型达到对系统进行降阶的目的,假定同步旋转坐标系的d轴与定子磁链方向一致,即ψsd=ψs,ψsq=0,且忽略定子绕组的电阻[8, 15]。Us为网侧电压,满足
| $ \left\{ \begin{array}{l} {\psi _{{\rm{r}}d}} = {L_{\rm{m}}}{U_{\rm{s}}}/\left( {{\omega _{\rm{s}}}{L_{\rm{s}}}} \right) + \sigma {i_{{\rm{r}}d}}/{L_{\rm{s}}},\\ {\psi _{{\rm{r}}q}} = \sigma {i_{{\rm{r}}q}}/{L_{\rm{s}}}。\end{array} \right. $ | (10) |
其中σ=LsLr-Lm2。
将式(10)代入式(8)后两项可得:
| $ \left\{ \begin{array}{l} \frac{{d{i_{{\rm{r}}d}}}}{{dt}} = \frac{{{L_{\rm{s}}}}}{\sigma }\left( {{u_{{\rm{r}}d}} - {R_{\rm{r}}}{i_{{\rm{r}}d}}} \right) + \left( {{\omega _{\rm{s}}} - p{\omega _{\rm{r}}}} \right){i_{{\rm{r}}q}},\\ \frac{{d{i_{{\rm{r}}q}}}}{{dt}} = \frac{{{L_{\rm{s}}}}}{\sigma }\left( {{u_{{\rm{r}}q}} - {R_{\rm{r}}}{i_{{\rm{r}}q}}} \right) - \left( {{\omega _{\rm{s}}} - p{\omega _{\rm{r}}}} \right)\left( {\frac{{{L_{\rm{m}}}{U_{\rm{s}}}}}{{\sigma {\omega _{\rm{s}}}}} + {i_{{\rm{r}}d}}} \right)。\end{array} \right. $ | (11) |
| $ \left\{ \begin{array}{l} {T_{\rm{e}}} = \frac{{3p{L_{\rm{m}}}}}{{2{L_{\rm{s}}}}}\left( {{\psi _{{\rm{s}}q}}{i_{{\rm{r}}d}} - {\psi _{{\rm{s}}d}}{i_{{\rm{r}}q}}} \right) = - \frac{{3{U_{\rm{s}}}p{L_{\rm{m}}}{i_{{\rm{r}}q}}}}{{2{L_{\rm{s}}}{\omega _{\rm{s}}}}},\\ {Q_{\rm{s}}} = \frac{3}{2}\left( {{u_{{\rm{s}}q}}{i_{{\rm{s}}d}} - {u_{{\rm{s}}d}}{i_{{\rm{s}}q}}} \right) = \frac{{3{U_{\rm{s}}}}}{{2{L_{\rm{s}}}}}\left( {\frac{{{U_{\rm{s}}}}}{{{\omega _{\rm{s}}}}} - {L_{\rm{m}}}{i_{{\rm{r}}d}}} \right)。\end{array} \right. $ | (12) |
对于一个单输入单输出非线性控制系统,
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{f}}\left( {t,x} \right) + \mathit{\boldsymbol{g}}\left( {t,x} \right)\mathit{\boldsymbol{u}}, $ | (13) |
其中x∈Rn和u∈R分别是系统的状态和输入;f(t, x)∈Rn可微有界;g(t, x)∈R是控制向量。根据期望的动态性能构建滑模变量s=s(t, x),若系统的动态性能稳定,则动态性能可表示为[11]:
| $ \mathit{\boldsymbol{\dot s}} = \underbrace {\frac{{\partial \mathit{\boldsymbol{s}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{s}}}}{{\partial \mathit{\boldsymbol{x}}}}\mathit{\boldsymbol{f}}\left( {t,x} \right)}_{\varphi \left( {t,x} \right)} + \underbrace {\overbrace {\frac{{\partial \mathit{\boldsymbol{s}}}}{{\partial \mathit{\boldsymbol{x}}}}\mathit{\boldsymbol{g}}\left( {t,x} \right)}^{B\left( {t,x} \right)}\mathit{\boldsymbol{u}}}_{h\left( {t,x} \right)}。$ | (14) |
式中:φ(t, x)是扰动项;h(t, x)是控制项。滑模控制由两部分组成[15]:等效输入ueq和切换输入uw,即
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{u}}_{{\rm{eq}}}} + {\mathit{\boldsymbol{u}}_{\rm{w}}}。$ | (15) |
1) 等效输入:可使系统在无外界干扰的情况下沿滑模面运动,影响着系统的响应速度和静态误差。若B(t, x)≠0,令
2)切换输入:使系统从任意初始阶段趋向于滑模面。自适应Super-twisting不需滑模变量一阶导数就可以使系统的滑模变量及其一阶导数在有限的时间内到达滑模面s(t, x)=
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_{\rm{w}}} = - \alpha {\left| \mathit{\boldsymbol{s}} \right|^{1/2}}{\rm{sign}}\;\mathit{\boldsymbol{s}} + \mathit{\boldsymbol{v}},\\ \mathit{\boldsymbol{\dot v}} = - \beta {\rm{sign}}\;\mathit{\boldsymbol{s}}。\end{array} \right. $ | (16) |
式中控制增益α,β满足
| $ \begin{array}{l} \dot \alpha = \left\{ \begin{array}{l} \omega \sqrt {\frac{\gamma }{2}} {\rm{sign}}\left( {\left| \mathit{\boldsymbol{s}} \right| - \mathit{\boldsymbol{u}}} \right),\alpha \ge {\alpha _{\rm{m}}};\\ \eta ,\alpha < {\alpha _{\rm{m}}}。\end{array} \right.\\ \beta = 2\varepsilon \alpha 。\end{array} $ | (17) |
ω,γ,u,η,ε,αm为任意的正实数。为避免滑模变量在滑模面附近时控制增益估值过高,增加抖振效应;同时又为防止滑模变量远离滑模面时控制增益估值过小,影响系统的快速性,建立一个观测区域M:{s, |s|≤u}。当s到达该区域,α(t),β(t)的取值开始下降,以降低脉动;当s离开该区域,α(t),β(t)的取值开始上升直至s再次进入该区域,以提高系统控制的快速性。文献[11]已对该算法稳定性进行了证明。
3.2 风力发电系统控制器设计为了实现风力发电系统发电功率在不同风区调节,并实现功率补偿,可以通过控制电磁转矩调节风机转速,进而控制发电机输出功率。这里选用加入积分环节的滑模变量sT, sQ,以消除静态误差,即
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{s}}_{\rm{T}}} = {T_{\rm{e}}} - {T^ * } + {c_{\rm{T}}}\int {\left( {{T_{\rm{e}}} - {T^ * }} \right){\rm{d}}t} ,\\ {\mathit{\boldsymbol{s}}_{\rm{Q}}} = {Q_{\rm{s}}} - {Q^ * } + {c_{\rm{Q}}}\int {\left( {{Q_{\rm{s}}} - {Q^ * }} \right){\rm{d}}t} 。\end{array} \right. $ | (18) |
式中:cT,cQ为积分系数;T*,Q*分别是电磁转矩参考值、无功功率参考值,其中T*由风速大小和额定功率决定,Q*可以根据网侧功率补偿的实际需要加以调整。对sT,sQ分别求一阶导数,可得:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot s}}}_{\rm{T}}} = {c_{\rm{T}}}\left( {{T_{\rm{e}}} - {T^ * }} \right) - {{\dot T}^ * } - \frac{{3p{L_{\rm{m}}}{U_{\rm{s}}}}}{{2{L_{\rm{s}}}{\omega _{\rm{s}}}}}\left\{ {\frac{{{L_{\rm{s}}}}}{\sigma } \times \left( {{u_{{\rm{r}}q}} - {R_{\rm{r}}}{i_{{\rm{r}}q}}} \right) - \left( {{\omega _{\rm{s}}} - p{\omega _{\rm{r}}}} \right)\left( {\frac{{{L_{\rm{m}}}{U_{\rm{s}}}}}{{\sigma {\omega _{\rm{s}}}}} + {i_{{\rm{r}}d}}} \right)} \right\},\\ {{\mathit{\boldsymbol{\dot s}}}_{\rm{Q}}} = {c_{\rm{Q}}}\left( {{Q_{\rm{s}}} - {Q^ * }} \right) - {{\dot Q}^ * } - \frac{{3{L_{\rm{m}}}{U_{\rm{s}}}}}{{2{L_{\rm{s}}}}}\left\{ {\frac{{{L_{\rm{s}}}}}{\sigma } \times \left( {{u_{{\rm{r}}d}} - {R_{\rm{r}}}{i_{{\rm{r}}d}}} \right) + \left( {{\omega _{\rm{s}}} - p{\omega _{\rm{r}}}} \right){i_{{\rm{r}}q}}} \right\}。\end{array} \right. $ | (19) |
其中
| $ \left\{ \begin{array}{l} \partial {{\mathit{\boldsymbol{\dot s}}}_T}/\partial {u_{{\rm{r}}q}} = - 3p{L_{\rm{m}}}{U_{\rm{s}}}/\left( {2{\omega _{\rm{s}}}\sigma } \right) \ne 0,\\ \partial {{\mathit{\boldsymbol{\dot s}}}_{\rm{Q}}}/\partial {u_{{\rm{r}}d}} = - 3{L_{\rm{m}}}{U_{\rm{s}}}/2\sigma \ne 0。\end{array} \right. $ | (20) |
从式(20)可知,此系统的相对度为1,可选用自适应Super-twisting滑模控制。滑模控制输入urq,urd可以分别表示为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_{{\rm{r}}q}} = {\mathit{\boldsymbol{u}}_{{\rm{r}}q{\rm{eq}}}} + {\mathit{\boldsymbol{u}}_{{\rm{r}}q{\rm{w}}}},\\ {\mathit{\boldsymbol{u}}_{{\rm{r}}d}} = {\mathit{\boldsymbol{u}}_{{\rm{r}}d{\rm{eq}}}} + {\mathit{\boldsymbol{u}}_{{\rm{r}}d{\rm{w}}}}。\end{array} \right. $ | (21) |
式中urqeq,urdeq为等效输入,可以通过令
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_{{\rm{r}}q{\rm{eq}}}} = - \frac{{2\sigma {\omega _{\rm{s}}}}}{{3p{L_{\rm{m}}}{U_{\rm{s}}}}}\left[ {{{\dot T}^ * } - {c_{\rm{T}}}\left( {{T^ * } - {T_{\rm{e}}}} \right)} \right] + {R_{\rm{r}}}{i_{{\rm{r}}d}} + \frac{{{\omega _{\rm{s}}} - p{\omega _{\rm{r}}}}}{{{L_{\rm{s}}}}}\left( {\frac{{{U_{\rm{s}}}{L_{\rm{m}}}}}{{{\omega _{\rm{s}}}}} + \sigma {i_{{\rm{r}}d}}} \right),\\ {\mathit{\boldsymbol{u}}_{{\rm{r}}q{\rm{w}}}} = - {\alpha _{\rm{T}}}{\left| {{\mathit{\boldsymbol{s}}_{\rm{T}}}} \right|^{1/2}}{\rm{sign}}\;{\mathit{\boldsymbol{s}}_{\rm{T}}} - \int {{\beta _{\rm{T}}}{\rm{sign}}\;{\mathit{\boldsymbol{s}}_{\rm{T}}}{\rm{d}}t} 。\end{array} \right. $ | (22) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_{{\rm{r}}d{\rm{eq}}}} = - \frac{{2\sigma }}{{3{L_{\rm{m}}}{U_{\rm{s}}}}}\left[ {{{\dot Q}^ * } + {c_{\rm{Q}}}\left( {{Q^ * } - {Q_{\rm{s}}}} \right)} \right] + {R_{\rm{r}}}{i_{{\rm{r}}d}} - \left( {{\omega _{\rm{s}}} - p{\omega _{\rm{r}}}} \right)\frac{{\sigma {i_{{\rm{r}}q}}}}{{{L_{\rm{s}}}}},\\ {\mathit{\boldsymbol{u}}_{{\rm{r}}d{\rm{w}}}} = - {\alpha _{\rm{Q}}}{\left| {{\mathit{\boldsymbol{s}}_{\rm{Q}}}} \right|^{1/2}}{\rm{sign}}\;{\mathit{\boldsymbol{s}}_{\rm{Q}}} - \int {{\beta _{\rm{Q}}}{\rm{sign}}\;{\mathit{\boldsymbol{s}}_{\rm{Q}}}{\rm{d}}t} 。\end{array} \right. $ | (23) |
式(22)(23)中αT、βT,αQ、βQ满足
| $ \left\{ \begin{array}{l} {{\dot \alpha }_{\rm{T}}} = \left\{ \begin{array}{l} {\omega _{\rm{T}}}\sqrt {\frac{{{\gamma _{\rm{T}}}}}{2}} {\rm{sign}}\left( {\left| {{\mathit{\boldsymbol{s}}_{\rm{T}}}} \right| - {u_{\rm{T}}}} \right),{\alpha _{\rm{T}}} \ge {\alpha _{{\rm{m}}t}};\\ {\eta _{\rm{T}}},{\alpha _{\rm{T}}} < {\alpha _{{\rm{m}}t}}。\end{array} \right.\\ {\beta _{\rm{T}}} = 2{\varepsilon _{\rm{T}}}{\alpha _{\rm{T}}}。\end{array} \right. $ | (24) |
| $ \left\{ \begin{array}{l} {{\dot \alpha }_{\rm{Q}}} = \left\{ \begin{array}{l} {\omega _{\rm{Q}}}\sqrt {\frac{{{\gamma _{\rm{Q}}}}}{2}} {\rm{sign}}\left( {\left| {{\mathit{\boldsymbol{s}}_{\rm{Q}}}} \right| - {u_{\rm{Q}}}} \right),{\alpha _{\rm{Q}}} \ge {\alpha _{{\rm{m}}q}};\\ {\eta _{\rm{Q}}},{\alpha _{\rm{Q}}} < {\alpha _{{\rm{m}}q}}。\end{array} \right.\\ {\beta _{\rm{Q}}} = 2{\varepsilon _{\rm{Q}}}{\alpha _{\rm{Q}}}。\end{array} \right. $ | (25) |
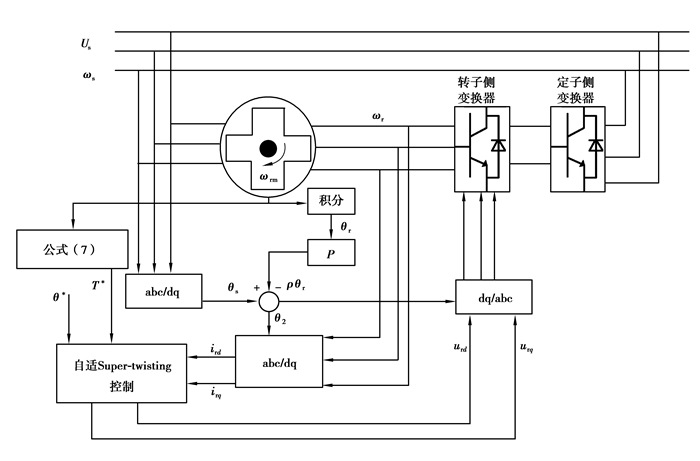
根据以上分析得该系统的结构图如图 4所示。
|
图 4 自适应Super-twisting控制器结构图 Figure 4 Control diagram of the adaptive Super-twisting controller |
笔者以30 kW小型水平轴变速恒频风电系统为算例,其主要参数如下:Prate=30 kW,ρ=1.224 kg/m3,vrate=8.95 m/s, kgb=25, J=3.662 kg·m2,R=7.3 m, β=0,λopt=8.1, Cpmax=0.41;双馈式发电机的参数:p=2,Rs=82 mΩ,Rr=228 mΩ,Lr=Ls=35.5 mH,Lm=35.7 mH;电网参数:Us=380 V,ωs=100 π(rad/s)。其中控制器参数选cT=1,ωT=20,γT=2,uT=3,ηT=0.1,εT=0.5,αmt=0.02,cQ=1,ωQ=10,γQ=2, uQ=2,ηQ=0.02,εQ=1,αmq=0.02。仿真连续运行260 s,以检验该控制方法的有效性。
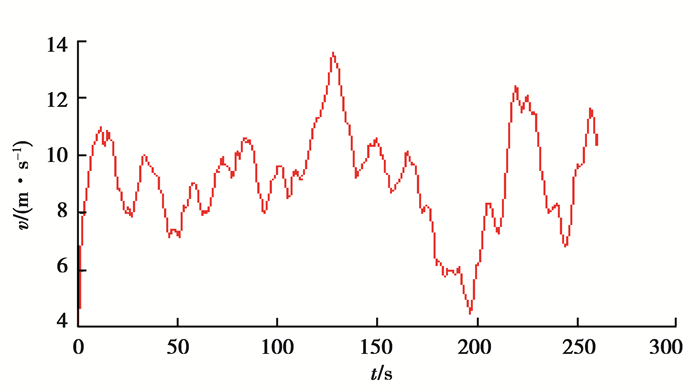
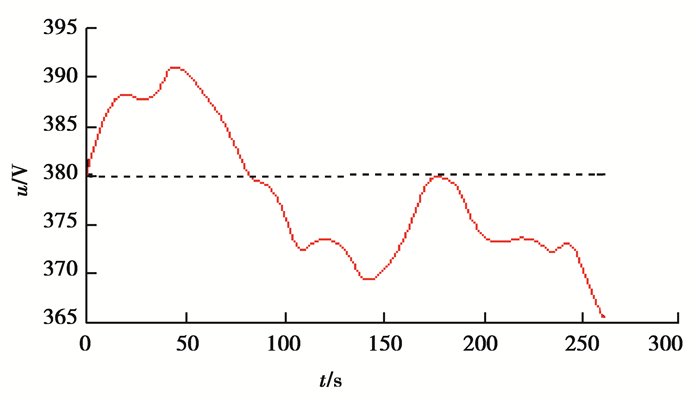
选用在额定风速附近波动的风速,风速曲线如图 5所示。同时,为验证控制系统对参数变化的鲁棒性,选用在额定电压附近波动且具有一定界限的网侧电压,网侧电压曲线如图 6所示。
|
图 5 风速曲线 Figure 5 Curve of wind speed |
|
图 6 网侧电压变化曲线 Figure 6 The voltage variable of grid |
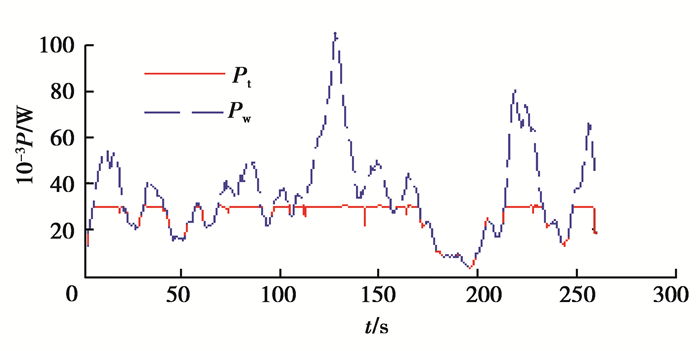
风机获得功率曲线如图 7所示,其中Pw为风机理论上可获得的最大功率,Pt为风机所获得的实际功率。从图可知,当Pw小于额定功率Prate时,风机工作于最大功率跟踪状态,具有良好的追踪性能;当Pw大于Prate时,限制发电功率,使风机工作于额定功率状态,避免因风力过大对风机造成破坏。
|
图 7 风机可获得最大功率Pw和实际获得功率Pt Figure 7 Maximum extractable power Pw and actual captured power Pt |
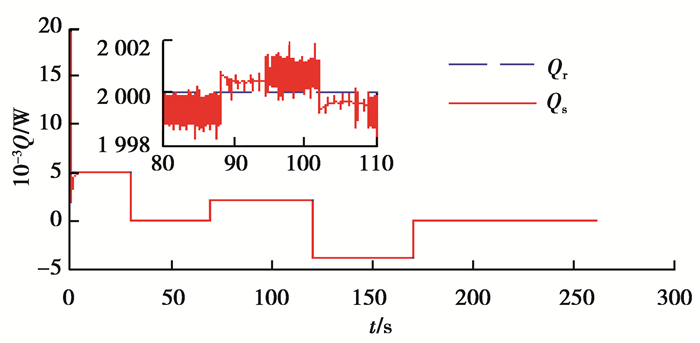
定子侧无功功率如图 8所示,定子侧无功功率根据电网功率补偿的实际需要调节,从图中可以看出无功功率的参考值与实际无功功率的误差在2 W之内,调节效果较好。同时从图 7和图 8可以看出当风速和电网电压波动时,有功功率和无功功率都能够快速调节,表明控制系统具有较强的鲁棒性。
|
图 8 定子侧无功功率Qs以及参考无功功率Qr Figure 8 stator reactive power Qs and its reference Qr |
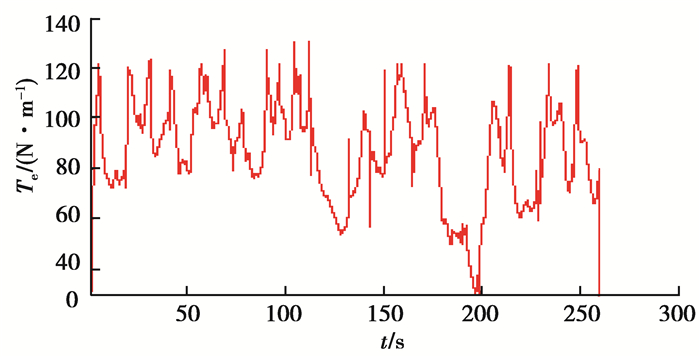
发电机的电磁转矩变化曲线如图 9所示,可知,电磁转矩变化基本平稳,可以有效减少电磁转矩因风速突变所造成的机械磨损,降低机械效应,提高风机的总体运行寿命。
|
图 9 风机电磁转矩 Figure 9 The electromagnetic torque of wind turbine |
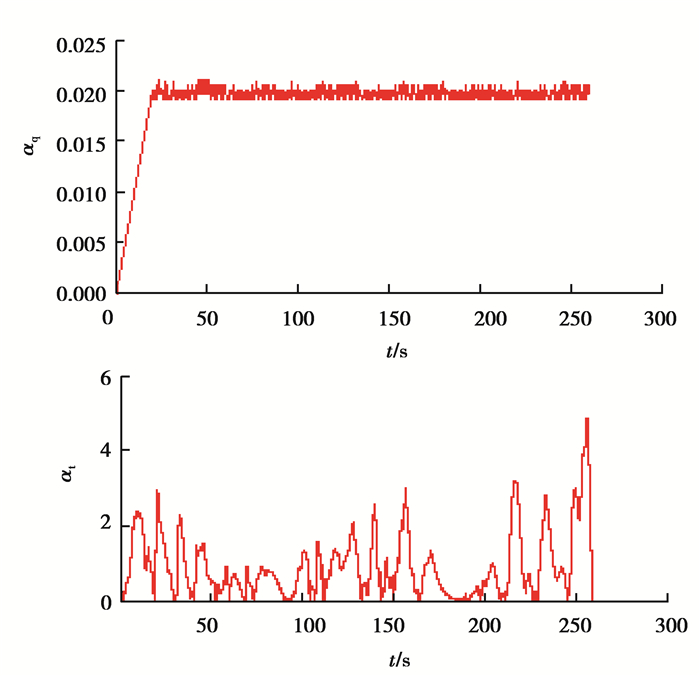
随着控制过程中风速的变化以及网侧电压的波动,为了提升系统的快速响应,需对切换控制增益做出适当调整,如图 10所示。
|
图 10 自适应增益变化 Figure 10 Adaptive gain variations |
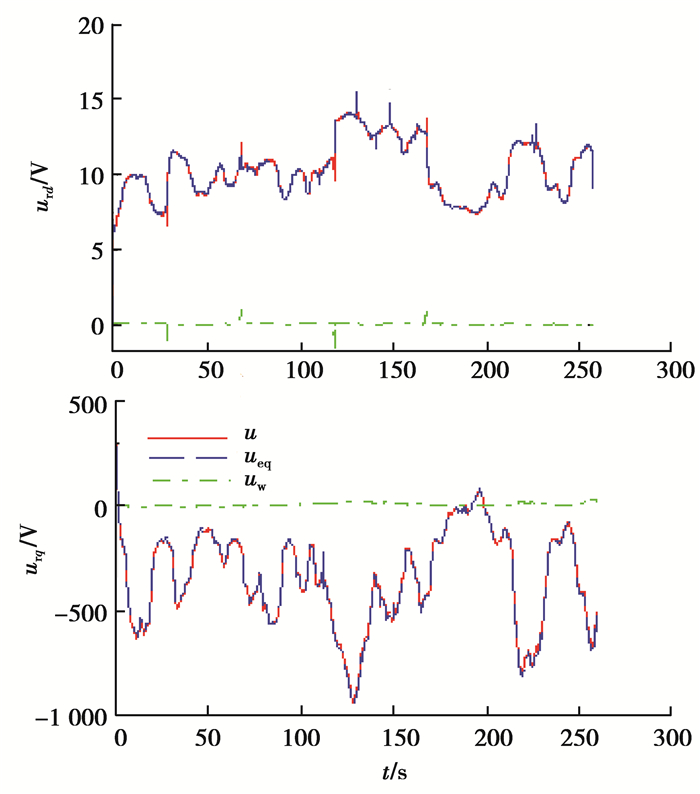
控制输入urq,urd以及其分量如图 11所示。从图知,随着风速的不停波动,等效输入迅速变化,切换输入在外界扰动和系统参数变化时,可有效提升系统的鲁棒性。同时可以看出控制输入的脉动较小,验证该控制方法具有降低抖振的作用。
|
图 11 控制输入电压以及对应组成部分 Figure 11 Control voltages and its components |
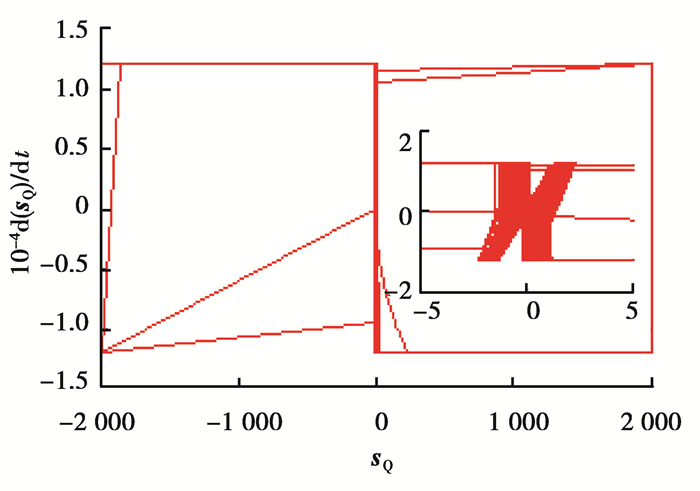
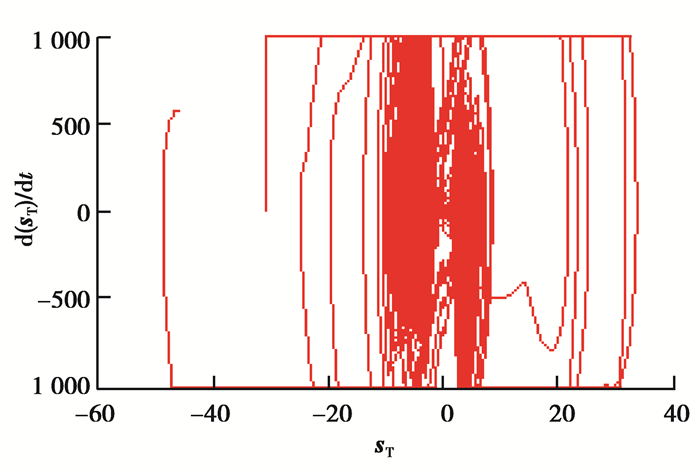
随着风速的变化,滑模变量sQ和sT与各自导数之间的收敛曲线如图 12、13所示,从图中可以看出,sQ和sT以及其一阶导数都在向滑模面s(t, x)=
|
图 12 在sQ- |
|
图 13 在sT- |
笔者提出一种新的控制方法来控制变速恒频风力发电系统,解决了其受电网电压波动、外界风速干扰而导致控制稳定性变差问题。首先,建立风力发电系统以及双馈式感应电机降阶模型,在此基础上将自适应Super-twisting控制方法应用于系统模型的控制器中。通过算例进行仿真分析,仿真结果表明所设计的控制器能够实现理想的控制效果,不仅具有很强的鲁棒性,且能实现控制增益随着系统运行状态的实时调整, 进而保证了系统的快速性,降低了滑模控制所固有的抖振效应。后续可与实际风机试验结合,进一步验证控制器的有效性。
| [1] |
年珩, 程鹏, 贺益康.
故障电网下双馈风电系统运行技术研究综述[J]. 中国电机工程学报, 2015, 35(16): 4184–4196.
NIAN Heng, CHENG Peng, HE Yikang. Review on operation techniques for DFIG-based wind energy conversion systems under network faults[J]. Proceedings of the CSEE, 2015, 35(16): 4184–4196. (in Chinese) |
| [2] |
杨涛, 刘国平, 黄淼.
双馈风电场柔性高压直流输电并网控制策略[J]. 重庆大学学报, 2015, 38(1): 1–11.
YANG Tao, LIU Guoping, HUANG Miao. A new control design for grid integration of DFIG wind farm with VSC-HVDC[J]. Journal of Chongqing University, 2015, 38(1): 1–11. (in Chinese) |
| [3] | Liu X X, Su X J, Song Y D. Switched control of repeated scalar non-linear systems via sliding mode control technique[J]. Iet Control Theory & Applications, 2017, 11(8): 1088–1097. |
| [4] | Chen J, Chen J, Gong C. On optimizing the aerodynamic load acting on the turbine shaft of PMSG-based direct-drive wind energy conversion system[J]. IEEE Transactions on Industrial Electronics, 2014, 61(8): 4022–4. DOI:10.1109/TIE.2013.2284148 |
| [5] | Kamal E, Oueidat M, Aitouche A. Robust scheduler fuzzy controller of DFIG wind energy systems[J]. IEEE Transactions on Sustainable Energy, 2013, 4(3): 706–715. DOI:10.1109/TSTE.2013.2242500 |
| [6] | Wang L, Zuo S, Song Y D, et al. Variable torque control of offshore wind turbine on spar floating platform using advanced RBF neural network[J]. Abstract and Applied Analysis, 2014(4): 1–7. |
| [7] |
王磊, 沈涛, 陈晨.
基于自适应神经网络的高阶非仿射变速风力机系统全局跟踪控制方法[J]. 太阳能学报, 2017, 38(8): 2083–2089.
WANG Lei, SHEN Tao, CHEN Chen. Universal tracking control method for high-order non-affine variable speed wind turbine system based on adaptive neural network[J]. Acta Energiae Solaris Sinica, 2017, 38(8): 2083–2089. (in Chinese) |
| [8] | Evangelista C A, Valenciaga F, Puleston P. Active and reactive power control for wind turbine based on a MIMO 2-sliding mode algorithm with variable gains[J]. IEEE Transactions on Energy Conversion, 2013, 28(3): 682–689. DOI:10.1109/TEC.2013.2272244 |
| [9] | Li P, Zheng Z. Robust adaptive second-order sliding-mode control with fast transient performance[J]. IET Control Theory Appl, 2012, 6(2): 305–312. DOI:10.1049/iet-cta.2010.0621 |
| [10] | Utkin V, Poznyak A. Adaptive sliding mode control with application to super-twist algorithm:Equivalent control method[J]. Automatica, 2013, 49(1): 39–47. DOI:10.1016/j.automatica.2012.09.008 |
| [11] | Shtessel Y, Taleb M, Plestan F. A novel adaptive-gain supert wisting sliding mode controller:Methodology and application[J]. Automatica, 2012, 48(5): 759–769. DOI:10.1016/j.automatica.2012.02.024 |
| [12] |
李鹏, 郑志强.
基于类二次型Lyapunov函数的Super-twisting算法收敛性分析[J]. 控制与决策, 2011, 26(6): 949–952.
LI Peng, ZHENG Zhiqiang. Convergence of super-twisting algorithm based on quadratic-like Lyapunov function[J]. Control and Decision, 2011, 26(6): 949–952. (in Chinese) |
| [13] | Wang L, Shen T, Chen C. Adaptive neural universal tracking control for high-order nonaffine varied-speed wind turbine system[C]//Proceedings of the 34th Chinese Control Conference, Hangzhou, 2015. [S. l. ]: IEEE, 2015: 7901-7905. |
| [14] | Merida J, Aguilar L, Davila J. Analysis and synthesis of sliding mode control for large scale variable speed wind turbine for power optimization[J]. Renewable Energy, 2014, 71(1): 715–728. |
| [15] | Valenciaga F, Evangelista C. 2-sliding active and reactive power control of a wind energy conversion system[J]. IET Control Theory and Applications, 2010, 4(11): 2479–2490. DOI:10.1049/iet-cta.2009.0437 |
 2018, Vol. 41
2018, Vol. 41



