1b. 重庆大学 重庆大学机械工程学院, 重庆, 400044;
2. 汽车噪声振动和安全技术国家重点实验室, 重庆, 400039
1b. College of Mechanical Engineering, Chongqing University, Chongqing 400044, P. R. China;
2. State Key Laboratory of Vehicle NVH and Safety Technology, Chongqing 400039, P. R. China
求解目标函数的最优解一直是学术界、工业界关注和研究的问题,近年来学术界已经提出并改进了很多优秀的优化算法并取得较好的解析解。随着计算机技术的进步, 进化算法也得到了飞速的发展。学者们从生物及其进化得到启发并提出一系列的进化算法,比如遗传算法、人工鱼群算法及蚁群算法等。这些算法都有各自的优点和缺点,但在高维、高度非线性的优化问题上往往容易陷入局部最优解而找不到全局最优解,这些算法的程序实现也比较复杂。
优化问题存在于很多的领域,比如无人驾驶汽车的路径规划[1]、数据处理[2]和计算机视觉、控制系统[3]、机械结构的参数优化等,其中涉及到的高维的优化问题往往很难得到较为准确的数值解。
用仿生算法求解这类优化问题都是对目标问题赋予初始解然后进行不断地迭代,直到目标函数达到终止的条件或者收敛到一个稳定的解。常用的仿生算法都是采用这样的步骤进行,比如常见的进化算法(进化策略算法、遗传算法(GA)、差分算法等),群体智能算法(粒子群算法(PSO)、人工蜂群算法(ABC)),SOS算法[4]、授粉算法(FPA))[5]以及回溯搜索算法[6]。
对于一些低维的问题,经典的优化方法能取得很好的结果,比如牛顿下山法、梯度下降法等,它们大都依赖目标函数的梯度信息[7],随着问题维数的增加和高度的非线性化,获取目标函数的梯度信息也就变得越来越困难。进化算法一般不需要目标函数的梯度信息,因此广泛应用于传统搜索算法解决不了的复杂问题或者高度非线性的优化问题中,但是仿生算法也存在搜索效率不够高、不稳定、可能收敛到局部最优解而得不到全局最优解[8],所以寻找一种高效的进化算法一直是学者们研究的方向。笔者在文化算法结构的基础上,将种群分为精英群体和普通群体,不同的群体按照不同的方式进化,普通群体在全局范围寻优,精英群体在其局部范围寻优,这样的进化方式保证了算法能够寻到全局最优解,并对初始种群进行了个体初始化,MATLAB实验表明改进的文化算法提高了求解优化问题的准确性和效率。
1 文化算法 1.1 优化问题背景介绍工程中遇到的各类优化问题可以概括性地表示为:
| $ \min f\left( \mathit{\boldsymbol{x}} \right):l \le \mathit{\boldsymbol{x}} \le u $ |
式中:f(x)表示高维的连续非线性目标函数,x=(x1, x2, …,xD)是D维向量;l, u为自变量x的上限和下限,并且满足关系:l≤u。
1.2 文化算法简介人们受到生物进化的启示先后提出了很多的算法用于解决生活中遇到的复杂问题,Dorigo在1991年受到蚁群捕食的启发提出了蚁群进化算法;Eberhard和Kennedy基于鱼群、鸟群提出了粒子群算法,这些遗传算法、进化策略等都属于传统的进化算法,它只能提供有限的或隐性的个体经验知识指导种群的进化,于是人们就想能不能利用显性机制来表达和指导种群的进化。
文化的社会内涵主要包含习惯、知识以及道德等,这些文化影响人们的社会活动并在人们的社会活动中不断的进化和升华,然后进一步指导和影响人们的社会活动,后来这一现象被学者们称之为文化进化机制。Reynolds基于进化算法和文化进化机制于1994年提出了双层进化结构的文化算法, 一开始算法的寻优速度比较慢,后来通过引入社会环境概念才使速度高于传统的生物进化算法[9]。
在微观层面(种群空间),个体不断地进化并形成知识,在宏观层面(信念空间),个体通过另外一种方法进化并指导种群空间中个体的进化,两个空间具有相应的通信协议,方便信息的交流。种群空间中个体具有较高的适应度值,其中的个体有较大的概率成为目标问题的最优解。
1.3 文化算法原理文化算法从框架上可以分为种群空间和信念空间两部分(见图 1),种群空间和信念空间分别通过不同的方式进行进化,种群空间基于种群进化,信念空间基于信念文化进化。首先种群空间的个体按照一定的进化规则进化,选择函数Accept()提取适应度强的个体信息,导致信念空间的进化并通过更新函数Update()更新, 信念空间则继续指导种群个体的进化,直到获得较好的种群个体(优化问题的最优解)[10]。
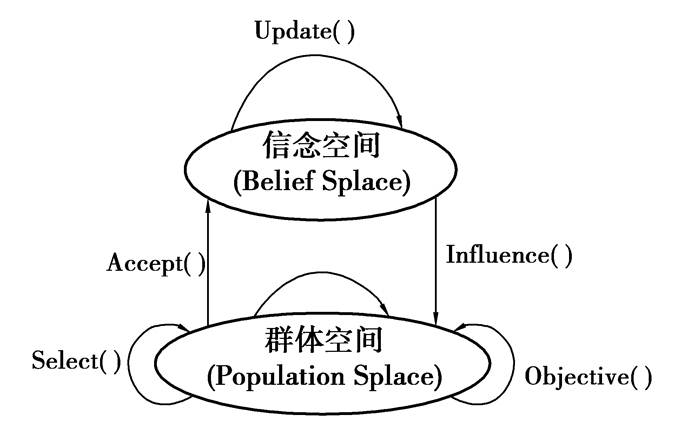
|
图 1 文化算法结构图 Figure 1 Structure of culture algorithm |
文化算法的特点:
1) 两个空间可以按照不同的进化方式及速度进化。
2) 双层进化系统,种群空间和信念空间分别继承各自父代的信息。
3) 文化算法支持不同算法的混合问题求解。
文化算法的特点决定了它能够解决复杂系统的问题[11]。
2 改进的文化算法 2.1 算法原理笔者对已有文化算法进行改进,提出了一种新型文化算法,该方法也是采用种群空间和信念空间双层结构,将种群空间划分为两个部分,其中适应度值高的一部分种群称之为精英群体(有丰富知识和文化,有自己的信仰且不会经常性地改变),剩下的部分称为普通群体(会被有知识和文化的群体所影响,个体差异也较大,易改变自己的信仰),对种群进行初始值优化,让种群个体在初始化阶段就尽可能地去逼近最优个体,提高寻找最优个体的速度及搜索的准确性。该方法容易理解,参数较少且易于编程实现,并进行了仿真实验对比,结果表明在高维非线性问题中改进后的文化算法表现出很好的性能。
文化算法可以通过很多的方法去实现,比较经典的文化算法实现收敛的速度很快,但很容易收敛到局部最优解[12],最近Yang等[13]提出一种实现方法称为CulQPSO,由于太多的控制变量使得实现起来比较麻烦。
文化算法的实现方法:该实现方法根据个体的适应度值将种群分为精英群体和普通群体,精英群体比普通群体有更高的适应度值,代表种群所信仰的“文化”。
精英群体中个体按照如下的方式进行进化:
| $ x{'_{i, j}} = \left\{ \begin{array}{l} {l_j} + {r_j}({u_j}{\rm{-}}{l_j}){\rm{, if}}\;|{x_{i, j}}{\rm{-}}{x_{k, j}}| \le \varepsilon ;\\ {x_{i, j}} + {\varphi _{i, j}}({x_{i, j}}{\rm{-}}{x_{k, j}}){\rm{, otherwise。}} \end{array} \right. $ | (1) |
式中:xi是优化方程的一组解;xi, j是xi第j个分量,j∈(1, 2,…, D);ε是人为设定的误差精度;xk是文化群体中另一个随机的解;rj是[0, 1]间的一个随机数;φi, j是[-1, 1]间的一个随机数。方程(1)采用的是人工蜂群的进化算法,随着xi, j和xk, j差值的减小,其步长也自适应地减小,如果步长减小为0, 或者小于ε,那么xi, j就随机地从[lj, uj]中随机选择;如果x′i, j超出了优化问题的边界,可以用下面的方法将其拉回到边界范围之内。
| $ x{'_{i, j}} = \left\{ \begin{array}{l} {l_j}, \;{\rm{if}}\;{x_{i, j}} + {\varphi _{i, j}}({x_{i, j}}{\rm{-}}{x_{k, j}}) < {l_j}{\rm{;}}\\ {u_j}{\rm{, if}}\;{x_{i, j}} + {\varphi _{i, j}}\left( {{x_{i, j}}{\rm{-}}{x_{k, j}}} \right) > {u_j}。\end{array} \right. $ | (2) |
普通群体中个体按照如下的方式进行进化[14]:
| $ x{'_{i, j}} = \left\{ \begin{array}{l} {x_{i, j}} + {\varphi _{i, j}}({x_{i, j}}{\rm{-}}{x_{k, j}}){\rm{, if}}\;{r_1} < C_{r, i}\;\;{\rm{or}}\;j = {r_j}\\ \;{x_{i, j}}{\rm{, otherwise。}} \end{array} \right. $ | (3) |
式中:Cr, i∈[0, 1]是交叉率;xk是整个种群中的随机解;r1∈[0, 1]的随机数;φi, j∈[-1, 1]的随机数;rj是1到D之间的随机整数。从方程(3)中可以看出,如果满足r1 < Cr, i or j=rj,普通群体中的个体后代是父代中个体的线性组合,否则子代就直接从父代继承,交叉率的取值也直接影响了普通群体中后代的继承方式,交叉率越大后代的多样性也就也大,该方法采用自适应的交叉率如下:
| $ {C_{r, i}} = \frac{{f({x_i})}}{{{\rm{max}}\;f}}{\rm{, }} $ | (4) |
式中:f(xi)为当前个体的适应度值;max f是种群个体的最大适应度值,随着进化的进行,伴随着种群的多样性下降,交叉率会逐渐减小,最终收敛到一个稳定的解。
在每代进化后都会从种群中根据适应度值的大小选择固定比例的个体作为精英群体,周而复始,直到收敛到一个稳定的最优解。从精英群体和普通群体的进化方式可以看出,精英群体从事局部范围的搜素,在精英个体周围去寻找更优的个体;普通群体从事全局范围的搜索,如果找到较好的个体就更新为精英个体,正是因为普通群体全局寻找个体,保证了该算法不会陷入局部最优解,两个群体分工合作,提高了搜索的效率。
2.2 种群的初始值优化种群个体初始值直接影响了优化问题收敛到最优解的速度、迭代的次数以及求解的稳定性,好的初始种群个体可以提高获得数值解的速度,减少迭代的次数[15]。
对于一维函数min f(x):l≤x≤u,其最优解出现在极小值点(点2)或者边界处(点1),通过对比边界值点和极小值点的目标函数值就可以确定最优解,如图 2所示。
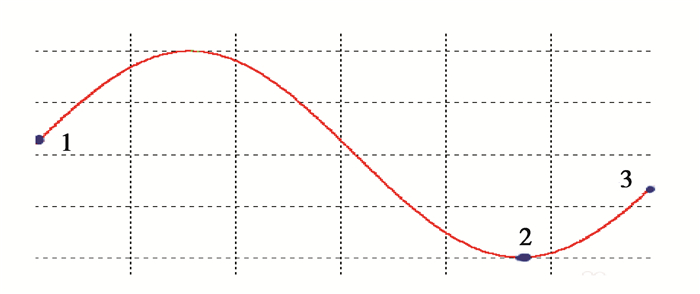
|
图 2 一维优化问题最优解分布图 Figure 2 Optimal solution distribution of 1-D problem |
对于二维函数min f(x):l≤x≤u,其最优解出现在谷底或者边界处,如图 3所示。
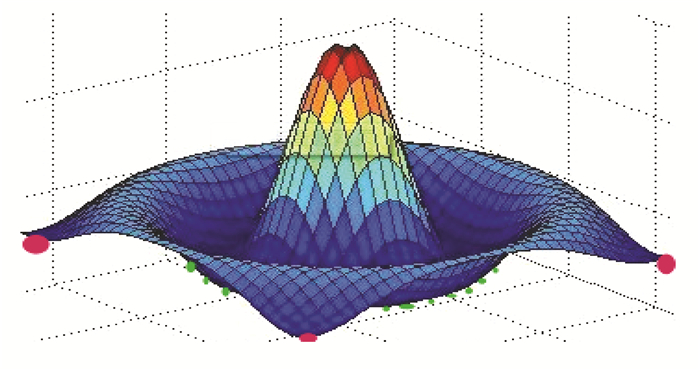
|
图 3 二维优化问题最优解分布图 Figure 3 Optimal solution distribution of 2-D problem |
图 3所表示目标函数的最优解大概率分布在谷底区域(图中绿色点所示)和边界区域(图中红色点所示区域),通过比较谷底和边界区域的函数值确定最优解。从一维优化问题和二维优化问题可以发现,最优解出现在边界处或者导数(偏导数)为零的概率较大。
实际工程中经常遇到高维的优化问题,可以通过分量偏导数的性质求得部分分量极小值点和边界条件的值作为初始化种群的备选值,从中取出对应的值初始化种群个体,使初始种群尽可能去接近最优解,从而达到提高搜索效率的目的。
对于要求解的优化问题,首先要对种群进行初始化,可以按照以下几个步骤进行:
1) 确定初始种群个体数量;
2) 对各个分量求偏导(可能只有一部分能求出),对能求出偏导的分量求出该分量的极小值点,并将其作为该分量的初始值;
3) 对于不能求出偏导的分量,在该分量上下限中随机选出一个值,作为该分量的初始值,完成种群个体的初始优化。
对于高维问题:f(X)=f(x1, x2, …, xD),D表示优化问题的维数,对其求导,如果关于xj的偏导数f′(xj)只含有xj一个自变量,就可以通过偏导数等于0获得xj的可能最优解集pj。所以可以按照下面的方法初始化种群个体:
| $ {x_{i, j}} = \left\{ \begin{array}{l} {\rm{random}}\;{\rm{of}}\;{p_j}{\rm{, }}\;\;{\rm{如果}}f'({x_j}){\rm{只含有}}{x_j};\;\\ {\rm{random}}\;{\rm{of}}\;{\rm{\;}}[{l_{j, }}{u_j}]{\rm{;}}\;\;\;{\rm{否则。}} \end{array} \right. $ | (5) |
在实际的工程问题中很多都是高维问题,对这些变量求偏导数可以获得优化问题最优解中变量的可能解集,在种群初始化过程中直接从该可能解集取值,减少该变量的寻优次数,相当于降低了问题的维数,可以更快收敛到最优解。
2.3 算法的MATLAB实现根据方程(5)初始化种群的个体xi
根据个体适应度值的大小,选出适应度值大的k%作为精英群体
WHILE终止条件不被满足DO
FOR每一个个体xi DO
IF xi是精英群体中的个体
采用方程(1)进化产生后代x′i,并计算相应的适应度值
ELSEIF xi是普通群体中的个体
采用方程(4)计算交叉率,
采用方程(3)进化(交叉、变异)产生后代x′i,并计算相应的适应度值
ENDIF
ENDFOR
从后代中选出适应度值大的k%作为精英群体
ENDWHILE
3 实验仿真Rastrigin函数因为有很多的局部最小值而常常被用来测试遗传算法,这里也用该函数测试新型文化算法的性能。
| $ {\rm{Ras}}\left( x \right) = 20 + x_1^2 + x_{^2}^2{\rm{-}}10({\rm{cos}}2{\rm{ \mathsf{ π} }}{x_1} + {\rm{cos}}2{\rm{ \mathsf{ π} }}{x_2})。$ |
实验选取精英群体的比例为40%,初始化种群个体数量为60,自变量下限为-10,上限为10, 迭代次数为100次,实验结果发现在40代左右算法就已经收敛,故选取前50次迭代数据作出图像, 结果如图 4所示。
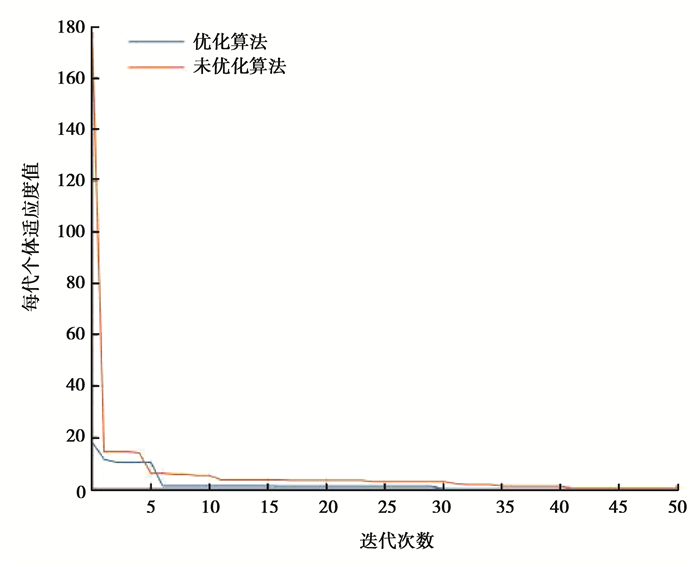
|
图 4 优化前后实验结果对比 Figure 4 Result contrast of optimized and origin |
从图 4所示的实验结果可以看出进行初始种群优化的算法性能远远高于未优化的算法,初始种群的适应度值更加接近收敛值,这一步就决定了优化后的算法有更高的收敛速度,提高了算法的效率。对于精英群体选取的比例,以及仿真实验的初始种群个体数量对算法的影响都还可以做进一步的研究和探讨。
在很多实际工程优化问题中都用该文化算法进行了求解,实验发现优化后的文化算法在速度和收敛性方面远远高于未优化的算法,并且在高维优化问题中,优势更加明显。
4 结论文化算法是基于人类进化机理而提出的一种寻优算法,将文化算法的种群分为两部分并进行初始种群优化可以提高算法寻优的速度,在稳定性、收敛性上表现出很好的性能,也进一步提高了算法的效率。针对不可求导的优化问题,该种群初始优化方法还具有一定的局限性,这也是后期重点研究的问题。
| [1] |
黎明, 江乐旗, 陈昊.
基于文化算法的无人飞行器航迹规划[J]. 模式识别与人工智能, 2017, 30(2): 152–161.
LI Ming, JIANG Leqi, CHEN Hao. Route planning method for unmanned aerial vehicle based on cultural algorithm[J]. Pattern Recognition and Artificial Intelligence, 2017, 30(2): 152–161. (in Chinese) |
| [2] |
朱志洁, 张宏伟, 王春明.
基于人工蜂群算法优化支持向量机的采场底板破坏深度预测[J]. 重庆大学学报, 2015, 38(6): 37–43.
ZHU Zhijie, ZHANG Hongwei, WANG Chunming. Prediction of floor damaged depth in working area based on support vector machine and artificial bee colony algorithm[J]. Journal of Chongqing University, 2015, 38(6): 37–43. DOI:10.11835/j.issn.1000-582X.2015.06.006 (in Chinese) |
| [3] |
刘新平, 吴晓玲, 张艳艳.
基于文化遗传算法的水浴温度模糊控制器设计[J]. 计算机测量与控制, 2015, 23(10): 3409–3411.
LIU Xinping, WU Xiaoling, ZHANG Yanyan. Fuzzy temperature controller design for Water-bath based cultural genetic algorithm[J]. Computer Measurement & Control, 2015, 23(10): 3409–3411. (in Chinese) |
| [4] | Cheng M Y, Prayogo D. Symbiotic organism search: A new metaheuristic optimization algorithm[J]. Computers Structures, 2014, 139: 98–112. DOI:10.1016/j.compstruc.2014.03.007 |
| [5] | Reynolds R G. An introduction to cultural algorithms[C]//Proceedings of the Third Annual Conference on Evolutionary Programming, San Diego, 1994. San Diego: [s. n], 1994: 131-139. |
| [6] | CMcioglu P. Backtracking search optimization algorithm for numerical optimization problem[J]. Applied Mathematics & Computation, 2013, 219(15): 8121–8144. |
| [7] |
姚新, 陈国良, 徐惠敏, 等.
进化算法研究进展[J]. 计算机学报, 1995, 18(9): 694–706.
YAO Xin, CHEN Guoliang, XU Huiming, et al. A survey of evolutionary algorithms[J]. Chinese Journal of Computers, 1995, 18(9): 694–706. (in Chinese) |
| [8] |
黄海燕, 顾幸生.
基于文化算法的神经网络及其在建模中的应用[J]. 控制与决策, 2008, 23(4): 477–480.
HUANG Haiyan, GU Xingsheng. Neural network based on cultural algorithms and its application on modeling[J]. Control and Decision, 2008, 23(4): 477–480. (in Chinese) |
| [9] | Engelbrecht A P. Computational intelligence: An introduction[C]//Internet of Things. 2nd ed. [S. l. ]: IEEE, 2007: 675-680. |
| [10] |
刘纯青. 文化算法及其应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2007. LIU Chunqing. Research on culture algorithm and their application[D]. Harbin: Harbin Engineering University, 2007. (in Chinese) |
| [11] | Yang K, Maginu K, Nomura H. Cultural algorithm-based quantum-behaved particle swarm optimization[J]. International Journal of Computer Mathematics, 2010, 87(10): 2143–2157. DOI:10.1080/00207160802676588 |
| [12] | Ali M Z, Reynolds R G. Cultural algorithms: A Tabu search approach for the optimization of engineering design problems[J]. Soft Computing, 2014, 18(8): 1631–1644. DOI:10.1007/s00500-013-1169-5 |
| [13] | Yang K, Maginu K, Nomura H. Cultural algorithm-based quantum-behaved particle swarm optimization[M]. . |
| [14] | Akay B, Karaboga D. A modified artificical bee colony algorithm for real-parameter optimization[J]. Information Sciences, 2012, 192(1): 120–142. |
| [15] |
李江云, 汪慧, 盛旺, 等.
用遗传算法进行RFD装置优化设计[J]. 重庆大学学报, 2016, 39(3): 13–20.
LI Jiangyun, WANG Hui, SHENG Wang, et al. Optimizition design of RFD set based on genetic algorithm[J]. Journal of Chongqing University, 2016, 39(3): 13–20. DOI:10.11835/j.issn.1000-582X.2016.03.002 (in Chinese) |
 2018, Vol. 41
2018, Vol. 41


