2. 重庆大学 输配电装备及系统安全与新技术 国家重点实验室, 重庆 400044;
3. 国网北京市电力公司, 北京 100045
2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China;
3. Dispatching Control Center, Jiangsu Electric Power Company, Nanjing 210024, P. R. China
电网可靠性评估方法需要对枚举或者抽样到的系统状态进行分析,包括解列判断、潮流计算、静态安全约束校验,以及运行约束背后的机组出力调整、负荷削减等校正措施[1],求解过程较为耗时,而为满足精度要求,电网可靠性评估又需要对大量系统状态进行分析,高度的计算复杂性严重制约了电网可靠性评估的实际工程应用[2-3]。
为提高电网可靠性评估的计算效率,现多从两个方面开展研究:①通过筛选关键系统状态减少分析数量。文献[4, 5]采用解析计算思路,对高阶系统状态截尾,减小了系统状态分析总数;文献[6-10]引入方差削减技术,在实现对可靠性指标无偏估计的前提下,通过改造抽样方式[6-8]或构造新的概率密度抽样函数[9, 10],提高了系统状态抽样的效率,有效减少了系统状态分析的数目。基于上述思路的类似研究较多,但为了达到较好的计算精度,仍需对数量庞大的系统状态进行分析,在系统状态分析速度未有效突破的情况下,可靠性评估仍然相当耗时。②通过改进负荷削减模型提高系统状态分析速度。文献[11-12]基于故障影响的同心松弛现象[13],提出启发式负荷削减模型;文献[14]提出基于拓扑变换的最大流模型;文献[15]为减少系统状态分析的计算量,提出一种用于识别偶发事件的函数型连接神经网络(FLNN)分类模型。上述模型从不同视角对负荷削减模型进行改进,但由于针对电网整体进行负荷削减计算,模型求解效率与电网整体规模大小耦合紧密,网络规模越大,计算越耗时。可见,建立计算时间与网络规模解耦的高效负荷削减模型对加速电网可靠性评估具有重要意义。
潮流灵敏度可以有效反映支路潮流与节点注入功率的互动关系,在连锁故障分析[16]、输电断面安全分析[17-18]、电网安全校正分析[19-20]等方面已有一定的研究。鉴于此,笔者提出一种基于潮流灵敏度的启发式负荷削减模型,该模型基于基态下的潮流灵敏度信息,通过推导故障状态下潮流灵敏度的解析表达式,实现故障状态下潮流灵敏度的快速计算;根据过载支路—节点注入功率的潮流灵敏度,提出发电机出力调整和负荷削减控制节点的选取规则,并基于反向等量配对原理构建基于潮流灵敏度的启发式负荷削减算法;此外,还提出配对节点组的功率调节量修正公式,消除了常规方法在调整中出现正常支路反复过载的拉锯现象,同时由于避免了潮流校验,有效提高了负荷削减计算速度。
1 故障系统状态潮流灵敏度的解析推导设除平衡节点外的电网节点数为NB,支路总数为NL,支路有功潮流组成的行向量为Pl,节点注入有功功率组成的行向量为Ps,节点电压相角组成的行向量为θs。由直流潮流方程可知,Pl不仅可表示为Ps的函数,还可表示为θs的函数。
| $ {P_1}\left( {{P_{\rm{s}}}} \right) = {P_1}\left( {{\theta _{\rm{s}}}} \right)。$ | (1) |
对上式等号两边同时求偏微分,可得下式:
| $ \Delta {P_1} = \frac{{\partial {P_1}}}{{\partial {P_{\rm{s}}}}}\Delta {P_{\rm{s}}} = \frac{{\partial {P_1}}}{{{\rm{d}}{P_{\rm{s}}}}}B - 1\Delta {P_{\rm{s}}} \\= X - {1_{NL \times NL}}A_{NB \times NL}^TB - {1_{NB \times NB}}\Delta {P_{\rm{s}}}, $ | (2) |
式中:XNL×NL为支路电抗组成的对角阵;ANB×NL为节点—支路关联矩阵;BNB×NB为节点电纳矩阵。
| $ \left\{ \begin{array}{l} {B_{ij}} = - \frac{1}{{{x_{ij}}}},\\ {B_{ii}} = \sum\limits_{\begin{array}{*{20}{c}} {j \in NB}\\ {j \ne i} \end{array}} {\frac{1}{{{x_{ij}}}}} ; \end{array} \right. $ | (3) |
式中:xij为支路(i, j)的电抗。由式(2)可知:
| $ {S_1} = \frac{{\partial {P_1}}}{{\partial {P_{\rm{s}}}}} = X - {1_{NL \times NL}}\mathit{\boldsymbol{A}}_{NB \times NL}^{\rm{T}}B - {1_{NB \times NB}}, $ | (4) |
式中:Sl为支路有功对节点注入有功的灵敏度矩阵,其推导隐含了一个假设,即平衡节点的机组出力随其他节点同步调整,以维持全网有功平衡。对发电机节点s,∂Pl/∂Ps表示节点s增加/减少单位出力,且平衡节点机组同步减少/增加单位出力时,支路l的有功潮流变化量;对负荷节点s,∂Pl/∂Ps表示节点s减少单位有功功率,同时平衡节点机组也减少单位出力时,支路l的有功潮流变化量。
电网可靠性评估需要对大量故障系统状态进行计算分析,式(4)虽然可直接求取每一故障状态下的潮流灵敏度矩阵,但由于涉及大规模矩阵求逆运算,求解较为耗时。因此,引入Wood-Bury矩阵求逆定理[21],基于基态下的潮流灵敏度矩阵信息推导故障系统状态下的潮流灵敏度矩阵的快速计算式。
由式(4)可知,潮流灵敏度矩阵Sl仅与网络拓扑结构和支路参数有关,当支路故障导致网络拓扑或支路参数改变,Sl也相应改变,但如果只有发电机故障,潮流灵敏度矩阵将保持不变。
设基态下的潮流灵敏度矩阵为S(0)l,即
| $ \mathit{\boldsymbol{S}}{\left( 0 \right)_1} = \frac{{\partial P{{\left( 0 \right)}_1}}}{{\partial {P_{\rm{s}}}}} = \mathit{\boldsymbol{X}}{\left( 0 \right)_{NL \times NL}} - 1\mathit{\boldsymbol{A}}{\left( 0 \right)_{NB \times NL}}^{\rm{T}}\mathit{\boldsymbol{B}}{\left( 0 \right)_{NB \times NB}} - 1, $ | (5) |
式中:X(0)NL×NL, A(0)NB×NL, B(0)NB×NB分别为基态下的支路电抗矩阵、节点-支路关联矩阵和节点电纳矩阵。
当电网出现支路故障,设故障支路总数为FL,正常支路总数为NL-FL,当前故障状态下的支路电抗矩阵、节点-支路关联矩阵和节点电纳矩阵分别为X(1)(NL-FL)×(NL-FL), A(1)NB×(NL-FL), B(1)NB×NB;ENL×NL为NL阶单位对角矩阵,其中由故障支路编号所对应的行向量组成的矩阵为LFL×NL,由正常支路编号对应的行向量组成的矩阵为L(NL-FL)×NL;则X(1)(NL-FL)×(NL-FL)、A(1)NB×(NL-FL)、B(1)NB×NB可表示为
| $ \mathit{\boldsymbol{A}}{\left( 1 \right)_{NB \times \left( {NL - FL} \right)}} = \mathit{\boldsymbol{A}}{\left( 0 \right)_{NB \times NL}}\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}^{\rm{T}}, $ | (6) |
| $ \mathit{\boldsymbol{X}}{\left( 1 \right)_{\left( {NL - FL} \right) \times \left( {NL - FL} \right)}} - 1 = {\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}}\mathit{\boldsymbol{X}}{\left( 0 \right)_{NL \times NL}} - 1\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}^{\rm{T}}, $ | (7) |
| $ \mathit{\boldsymbol{B}}{\left( 1 \right)_{NB \times NB}} = \mathit{\boldsymbol{B}}{\left( 0 \right)_{NB \times NB}} + \Delta {\mathit{\boldsymbol{B}}_{NB \times NB}}, $ | (8) |
| $ \begin{array}{l} \Delta {\mathit{\boldsymbol{B}}_{NB \times NB}} = - \left( {\mathit{\boldsymbol{A}}{{\left( 0 \right)}_{NB \times NL}}\mathit{\boldsymbol{L}}_{FL \times NL}^{\rm{T}}} \right) \times \\ \left( {{\mathit{\boldsymbol{L}}_{FL \times NL}}\mathit{\boldsymbol{X}}{{\left( 0 \right)}_{NL \times NL}} - 1\mathit{\boldsymbol{L}}_{FL \times NL}^{\rm{T}}} \right){\left( {\mathit{\boldsymbol{A}}{{\left( 0 \right)}_{NB \times NL}}\mathit{\boldsymbol{L}}_{FL \times NL}^{\rm{T}}} \right)^{\rm{T}}}。\end{array} $ | (9) |
将式(6)(9)代入式(4),故障系统状态下的灵敏度矩阵为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_1} = \left( {{\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}}\mathit{\boldsymbol{X}}{{\left( 0 \right)}_{NL \times NL}} - 1\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}^{\rm{T}}} \right){{\left( {\mathit{\boldsymbol{A}}{{\left( 0 \right)}_{NB \times NL}}\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}^{\rm{T}}} \right)}^{\rm{T}}} \times }\\ {\left[ {\mathit{\boldsymbol{B}}{{\left( 0 \right)}_{NB \times NB}} - \left( {\mathit{\boldsymbol{A}}{{\left( 0 \right)}_{NB \times NL}}\mathit{\boldsymbol{L}}_{FL \times NL}^{\rm{T}}} \right)\left( {{\mathit{\boldsymbol{L}}_{FL \times NL}}\mathit{\boldsymbol{X}}{{\left( 0 \right)}_{NL \times NL}} - 1\mathit{\boldsymbol{L}}_{FL \times NL}^{\rm{T}}} \right) \times } \right.}\\ {\left. {{{\left( {\mathit{\boldsymbol{A}}{{\left( 0 \right)}_{NB \times NL}}\mathit{\boldsymbol{L}}_{FL \times NL}^{\rm{T}}} \right)}^{\rm{T}}}} \right] - 1。} \end{array} $ | (10) |
根据Wood-Bury矩阵修正引理,可对公式(10)作如下变换:
| $ \begin{array}{l} {\mathit{\boldsymbol{S}}_1} = {\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}}\mathit{\boldsymbol{X}}{\left( 0 \right)_{NL \times NL}} - 1\left( {\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}^{\rm{T}}{\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}}} \right) \times \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{A}}{\left( 0 \right)_{NB \times NL}}^{\rm{T}}\mathit{\boldsymbol{B}}{\left( 0 \right)_{NB \times NB}} - 1 \times \\ \;\;\;\;\;\;\;\left[ {{\mathit{\boldsymbol{E}}_{NB \times NB}} - {\mathit{\boldsymbol{M}}_{NB \times FL}}\left( {{\mathit{\boldsymbol{W}}_{FL \times FL}} + \mathit{\boldsymbol{M}}_{NB \times FL}^{\rm{T}}\mathit{\boldsymbol{B}}{{\left( 0 \right)}_{NB \times NB}} - 1{\mathit{\boldsymbol{M}}_{NB \times FL}}} \right) - } \right.\\ \;\;\;\;\;\;\;\left. {1\mathit{\boldsymbol{M}}_{NB \times FL}^{\rm{T}}\mathit{\boldsymbol{B}}{{\left( 0 \right)}_{NB \times NB}} - 1} \right]。\end{array} $ | (11) |
式中:WFL×FL=LFL×NLX(0)NL×NLLFL×NLT;MNB×FL=A(0)NB×NLTLFL×NL。
经进一步推导,式(11)可表示为如下形式:
| $ \begin{array}{l} {\mathit{\boldsymbol{S}}_1} = {\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}}\mathit{\boldsymbol{X}}{\left( 0 \right)_{NL \times NL}} - 1\mathit{\boldsymbol{A}}{\left( 0 \right)_{NB \times NL}}^{\rm{T}}\mathit{\boldsymbol{B}}{\left( 0 \right)_{NB \times NB}} - 1 \times \\ \;\;\;\;\;\;\;\left[ {{\mathit{\boldsymbol{E}}_{NB \times NB}} - {\mathit{\boldsymbol{M}}_{NB \times FL}}\left( {{\mathit{\boldsymbol{W}}_{FL \times FL}} + \mathit{\boldsymbol{M}}_{NB \times FL}^{\rm{T}}\mathit{\boldsymbol{B}}{{\left( 0 \right)}_{NB \times NB}} - 1{\mathit{\boldsymbol{M}}_{NB \times FL}}} \right) - } \right.\\ \;\;\;\;\;\;\;\left. {1\mathit{\boldsymbol{M}}_{NB \times FL}^{\rm{T}}\mathit{\boldsymbol{B}}{{\left( 0 \right)}_{NB \times NB}} - 1} \right]\\ \;\;\;\;\;\;\; = {\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}}\mathit{\boldsymbol{S}}{\left( 0 \right)_1}\left( {{\mathit{\boldsymbol{E}}_{NB \times NB}} - {\mathit{\boldsymbol{M}}_{NB \times FL}}{\mathit{\boldsymbol{K}}_{FL \times FL}}\mathit{\boldsymbol{M}}_{NB \times FL}^{\rm{T}}\mathit{\boldsymbol{B}}{{\left( 0 \right)}_{NB \times NB}} - 1} \right)。\end{array} $ | (12) |
式中:KFL×FL= (WFL×FL+MNB×FLTB(0)NB×NB-1MNB×FL)-1 。
由于输电线路和变压器等支路的故障概率通常很小,因此,出现多条支路同时故障的概率也很小,即FL一般较小,因此,WFL×FL, KFL×FL与MNB×FL的阶数也较小,由于基态下的S(0)l和B(0)NB×NB-1为已知量,故求取Sl涉及的主要计算量为FL阶矩阵的求逆,如果采用式(4)计算Sl,则涉及NL阶矩阵的求逆,可见式(12)使得求取故障系统状态下灵敏度矩阵所需计算量大幅降低。
令FNB×NB=MNB×FLKFL×FLMNB×FLT,式(12)可简化为
| $ {S_1} = {\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}}\mathit{\boldsymbol{S}}{\left( 0 \right)_1}\left( {{\mathit{\boldsymbol{E}}_{NB \times NB}} - {\mathit{\boldsymbol{F}}_{NB \times FB}}\mathit{\boldsymbol{B}}{{\left( 0 \right)}_{NB \times NB}} - 1} \right)。$ | (13) |
综上所述,对于任意故障系统状态,潮流灵敏度矩阵的快速计算解析表达式为
| $ {S_1} = \left\{ {\begin{array}{*{20}{c}} {S{{\left( 0 \right)}_1}}&{发电机故障,}\\ {{\mathit{\boldsymbol{L}}_{\left( {NL - FL} \right) \times NL}}\mathit{\boldsymbol{S}}{{\left( 0 \right)}_1}\left( {{\mathit{\boldsymbol{E}}_{NB \times NB}} - {\mathit{\boldsymbol{F}}_{NB \times FB}}\mathit{\boldsymbol{B}}{{\left( 0 \right)}_{NB \times NB}} - 1} \right)}&{支路型故障;} \end{array}} \right. $ | (14) |
任意故障系统状态下的支路潮流表达式为
| $ {P_1} = {S_1}{P_{\rm{s}}}。$ | (15) |
本节潮流灵敏度矩阵的快速计算表达式适用于发电机故障或不引起网络解列的支路型故障。对于导致网络解列的支路故障,可直接采用式(4)计算各解列子网络的潮流灵敏度矩阵,并采用式(15)求取各解列子网络的支路有功潮流。由于支路故障导致网架解列的故障系统状态并不多,即绝大多数抽取到的故障系统状态并不会出现网络解列,都可采用式(14)进行计算,因此,本节推导仍具很好的实用性。
2 控制节点的选取规则潮流灵敏度矩阵可有效揭示支路有功潮流对节点注入有功的敏感程度,选取灵敏度大的节点为控制节点,通过改变控制节点的有功注入可有效缓解或消除支路过载。若过载支路有功潮流实际流向与潮流分布计算所规定的参考方向相同,则对潮流灵敏度为正和为负的控制节点,分别降低和增加节点注入有功功率;反之,若过载支路有功潮流的实际流向与潮流参考方向相反,则对其潮流灵敏度为正或为负的控制节点,应分别增加或降低对应节点注入有功功率。
为便于下一节启发式反向等量配对负荷削减模型的描述,对式(13)灵敏度矩阵作如下变换:令对角阵D=E(NL-FL)×(NL-FL)×[d1, d2, …, d(NL-FL)]T表征支路有功潮流实际流向与潮流计算参考方向的一致性信息,其中第l行对角元素dl的取值为:若支路l有功潮流实际流向与参考方向相同,dl=1;反之dl=-1。考虑方向一致性信息后对式(13)变换如下:
| $ {S_1} = {L_{\left( {NL - FL} \right) \times NL}}S{\left( 0 \right)_1}\left( {{E_{NB \times NB}} - {F_{NB \times FB}}B{{\left( 0 \right)}_{NB \times NB}} - 1} \right)D。$ | (16) |
经过变换后,式(16)的Sl已是以支路实际有功潮流方向作为参考方向的潮流灵敏度。根据过载支路有功潮流对节点注入有功的灵敏度信息,对发电机和负荷控制节点采用如下规则进行筛选:
设过载支路编号为l,发电机节点i的实际出力为PG, i,其有功出力的上下限为(PG, imax, PG, imin),负荷节点j的有功负荷为PL, j,在灵敏度矩阵Sl的第l行中,令第i列和第j列元素分别为Sl, i和Sl, j。
① 对发电机节点i:当Sl, i>0且PG, i-PG, imin>0时,选节点i为减出力的发电机控制节点,即减小发电机有功出力以降低支路l过载程度;当Sl, i < 0且PG, imax-PG, i>0时,选节点i为加出力的发电机控制节点,即增加发电机有功出力以降低支路l的过载程度。
② 对负荷节点j:当Sl, j < 0时,选节点j为切负荷控制节点,即切除部分负荷可降低支路过载程度。
3 启发式反向等量配对负荷削减模型基于潮流灵敏度的常规启发式负荷削减模型按照潮流灵敏度的绝对值大小对控制节点进行降序排序,并按此顺序依次调整节点注入功率,在节点注入功率调整过程中引起的系统有功不平衡量默认由平衡节点机组来平衡,同时在节点注入功率调整过程中往往忽略对正常支路有功潮流的影响,容易导致平衡节点机组出力越限和引起正常支路潮流过载等问题。据此,采用反向等量配对调节原理,使配对节点组的注入功率调节量大小相等,方向相反,从而降低对平衡节点机组的有功变动要求,以避免其出力越限;同时,在计及配对节点组功率调节量对正常支路影响的基础上,提出反向配对控制节点组的功率调节量修正公式,以防止调节中引起正常支路过载,有效避免了常规方法为防止正常支路过载所需的反复潮流校验过程。
3.1 反向等量配对调节算法流程基于过载支路有功潮流对节点注入有功的潮流灵敏度,采用反向等量配对调节思路:对每一个加出力控制节点配对一个减出力控制节点,形成配对节点组,并在节点注入功率调整中保持节点组加、减出力的功率调节量相等。按此方式,可有效避免配注入功率调整引起的系统有功不平衡。
反向等量配对调节的算法流程如下:
① 确定当前控制节点:建立加出力发电机控制节点集ξG, +,减出力发电机控制节点集ξG, -和切负荷控制节点集ξL, -。
② 将各集合所包含的控制节点分别按潮流灵敏度绝对值降序排列,将切负荷控制节点看作反向加出力的发电机控制节点,并为尽可能避免切负荷,令ξG', +=ξG, +∪ξL, -,将ξL, -排在ξG, +的后面。
③ 从(ξG', +, ξG, -)首端各取一个控制节点构成配对节点组,根据功率调节量的计算公式进行注入功率调整(详见3.2节)。在实际计算中,每次配对节点组的注入功率调整完毕,其中至少有一个控制节点达到最大调节能力,此时将该控制节点从相应的控制节点集合中删除。
④ 根据式(2)计算过载支路的有功潮流改变量,判断过载现象是否消除,若是,记录切负荷量,算法流程结束;否则,转③。
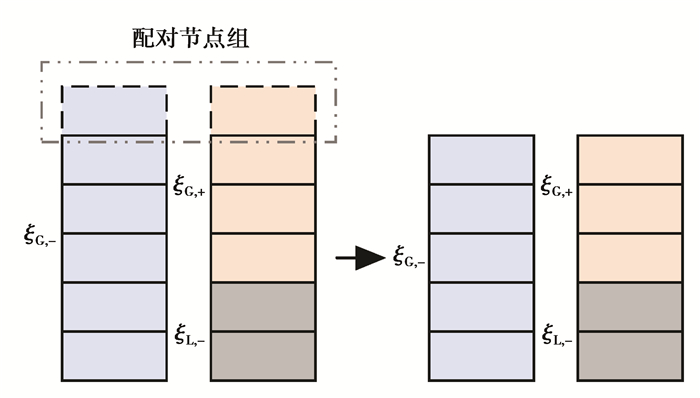
图 1给出了反向等量配对原理的示意图。
|
图 1 反向等量配对示意图 Figure 1 Illustration of adjustment for reverse equivalent pairing |
需注意,在算法流程的步骤③中,在配对调整后已达最大调节能力的控制节点将从控制节点集合中不断被移除,最终可能导致ξG', +、ξG, -其中之一为空集的情况,此时节点注入有功调节过程不再进行配对调节,而是在非空的控制节点集与平衡节点之间开展注入功率调整。
3.2 功率调节量的计算设节点i为减出力控制节点,节点j为加出力控制节点,两者构成配对节点组i-j。对任一条支路l,节点组的潮流灵敏度为
| $ {S_{1,i - j}} = {S_{1,i}} - {S_{1,j}}。$ | (17) |
对支路l,若该支路为过载支路,Sl, i-j>0始终成立,调整配对节点组注入功率将缓解支路l过载程度;但对于其他正常支路,可能存在Sl, i-j < 0,即配对节点组功率的调整将使正常支路潮流升高。
为实现对过载支路潮流有效快速的校正调节,对配对节点组的功率调整量分析如下:
① 针对过载支路,通过调整节点组功率消除支路过载的功率调节量为
| $ \Delta {P_1} = \frac{{\left( {{P_1} - P_1^{\max }} \right)}}{{{S_{1,i - j}}}}, $ | (18) |
式中:Plmax为过载支路的传输容量。
② 针对节点组i-j,节点组调节能力受节点i的可减功率范围和节点j可加功率范围的制约,节点组调节量不能大于如下值:
| $ \Delta {P_2} = \min \left\{ {\left( {{P_i} - P_i^{\min }} \right),\left( {P_j^{\max } - {P_j}} \right)} \right\}, $ | (19) |
式中:(Pi, Pj)为节点i与节点j的实际注入功率;Pimin和Pjmax分别为节点i的最小和最大注入功率。
③ 针对正常支路,考虑到重载和受调节影响较大的正常支路可能在调节中过载,应保证调节过程不引起这两类支路过载。设重载支路与受调节影响较大的正常支路组成的集合为(ψ1, ψ2):
a.若|Pl|>0.9Plmax,当前支路属于重载型线路,此时l∈ψ1;
b.若Sl, i-j < -a(a为预设阀值,本文取0.05),此时该支路潮流随配对节点组注入功率调节而变化敏感,支路有功潮流增量可能较大,过载的可能性也较大,此时l∈ψ2。
为保证启发式调节过程中正常支路不过载。配对节点组的功率调节量不应大于如下值:
| $ \Delta {P_3} = \min \left\{ {\mathop {\min }\limits_{1 \in \psi 1} \left( {\frac{{\left( {P_{1,i}^{\max } - {P_{1,i}}} \right)}}{{\left| {{S_{1,i - j}}} \right|}}} \right),\mathop {\min }\limits_{l \in \psi 2} \left( {\frac{{\left( {P_{1,i}^{\max } - {P_{1,i}}} \right)}}{{\left| {{S_{1,i - j}}} \right|}}} \right)} \right\}, $ | (20) |
式中:Pl, imax, Pl, i分别为支路传输容量和实际有功潮流。
综上所述,配对节点组i-j的功率调节量为
| $ \Delta {P_{i - j}} = \min \left\{ {\Delta {P_1},\Delta {P_2},\Delta {P_3}} \right\}。$ | (21) |
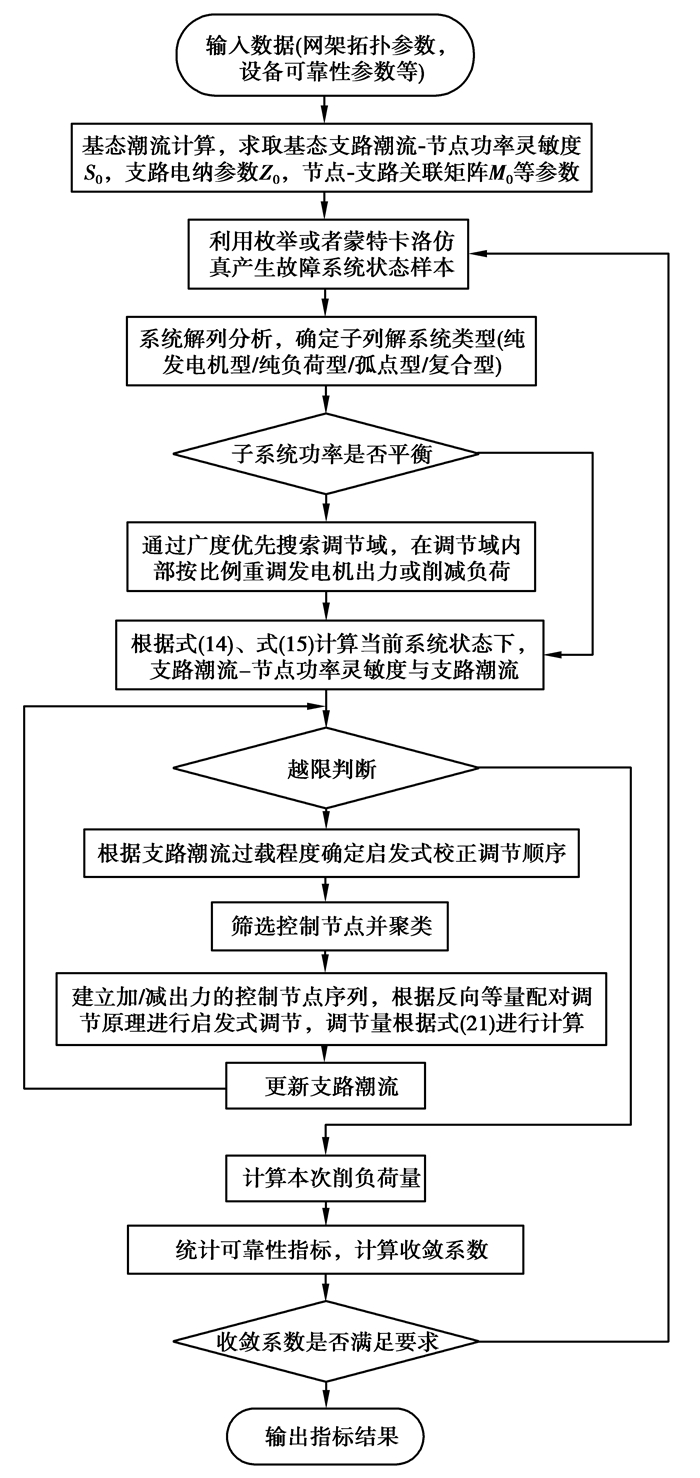
电网可靠性评估的算法流程如图 2所示,其中系统状态分析部分的流程为
|
图 2 电网可靠性评估流程 Figure 2 Process of reliability evaluation for power grid |
① 计算基态下的潮流分布P(0)l和支路有功对节点注入有功的灵敏度矩阵S(0)l;
② 基于基态潮流灵敏度矩阵S(0)l,对抽取到的故障系统状态采用式(14)计算灵敏度矩阵Sl,采用式(15)计算支路潮流Pl;
③ 越限判断,确定是否有支路过载;若是,转式(4);否则,转式(8);
④ 筛选当前过载支路对应的控制节点;
⑤ 建立加/减出力的控制节点排列,按照反向等量配对调节原理进行启发式调节,配对节点组功率调节量根据式(21)进行计算;
⑥ 若当前过载支路被消除,记录发电机控制节点与切负荷节点的可调功率和切负荷量,转入下一条过载支路的校正调节;否则,转式(7);
⑦ 若所有过载支路均被校正完毕,计算总切负荷量,进行系统可靠性指标的累加统计;抽取下一个故障系统状态,转步骤②。
5 算例分析 5.1 模型有效性验证采用非序贯蒙特卡洛仿真对RBTS[22],IEEE-RTS79和IEEE-RTS96[23]可靠性测试系统按如下3个方案进行可靠性评估分析。
方案1:基于直流潮流的线性规划最优负荷削减模型[1]。
方案2:基于潮流灵敏度的常规启发式负荷削减模型,即根据过载支路有功对控制节点注入有功灵敏度的绝对值降序排列,依次序调整节点注入有功,故障系统状态下的潮流灵敏度矩阵采用式(4)计算,控制节点的功率调节量按下式确定。为避免调整导致正常支路过载,每次调节后都进行潮流校验。
| $ \Delta {P_{i - j}} = \min \left\{ {\Delta {P_1},\Delta {P_2}} \right\}。$ | (22) |
方案3:基于本文潮流灵敏度及反向等量配对启发式负荷削减模型。
表 1给出了不同方案下的可靠性指标。可见:
| 表 1 不同负荷削减模型下的可靠性评估结果 Table 1 Reliability evaluation results for different load shedding schemes |
① 基于潮流灵敏度的启发式负荷削减模型进行电网可靠性评估,所得可靠性指标与线性规划最优负荷削减模型很接近,这说明基于潮流灵敏度的启发式负荷削减模型的计算精度能够满足要求。
② 与线性规划最优负荷削减模型相比,基于潮流灵敏度的启发式负荷削减模型所得可靠性指标偏大。这是因为:线性规划最优负荷削减模型进行全网发电机出力优化调整和负荷削减优化,而基于潮流灵敏度的启发式负荷削减模型采用启发式调节思路,通过部分控制节点上的发电机出力调整或负荷削减以消除支路过载现象,是局部优化调整,因此,负荷削减量比线性规划最优负荷削减模型偏大,但计算时间会明显降低。
③ 随着电网规模增大,基于潮流灵敏度的启发式负荷削减模型与线性规划最优负荷削减模型所得可靠性指标的相对误差逐渐减小。这是因为电网规模越大,采用基于潮流灵敏度的启发式负荷削减模型时,能够进行节点注入有功调节的控制节点数也越多,这种局部优化调整的效果越接近全网优化调整;反之电网规模越小,控制节点的数目也越少,在局部控制节点进行发电机出力调整以消除支路过载的效果比较有限,此时往往需要进行负荷削减才能使系统恢复正常。以线性规划最优负荷削减模型的结果为参照基准,表 2给出了基于潮流灵敏度的启发式负荷削减模型所得指标的相对误差情况。可见,与常规启发式负荷削减模型相比,本文模型相对误差更小,这验证了本文模型具有更好的准确性。
| 表 2 可靠性指标误差比较 Table 2 Comparison of reliability indices error |
采用增益系数作为评判依据,比较基于灵敏度的启发式负荷削减模型的计算效率,定义如下:
| $ \eta = \frac{{{t_B}\sigma _B^2}}{{{t_A}\sigma _A^2}}, $ | (23) |
式中:(tA, σA)和(tB, σB)为分别为采用方法A和B的计算耗时和方差系数,其中方差系数σ是计算准确性的衡量依据,其表达式如下:
| $ \sigma = \frac{{\sqrt {Var\left( {\hat L} \right)} }}{{\hat L}}, $ | (24) |
式中:
当η>1,方法B计算效率优于方法A;η越大,方法B计算优势越明显,反之当η < 1,方法B计算效率比方法A差。
表 3给出了基于潮流灵敏度的负荷削减模型相对线性规划最优负荷削减模型的增益系数。可见,基于潮流灵敏度的负荷削减模型的增益系数大于1,这说明其计算效率优于线性规划最优负荷削减模型。原因在于:线性规划最优负荷削减模型的计算速度与系统规模相关,系统规模越大,计算速度越慢;而基于潮流灵敏度的启发式负荷削减模型是启发式局部优化调整,计算效率受系统规模影响较小。随着网络规模增大,基于潮流灵敏度的启发式负荷削减模型具有更高的计算效率。
| 表 3 增益系数对比结果 Table 3 Comparison result of gain coefficient |
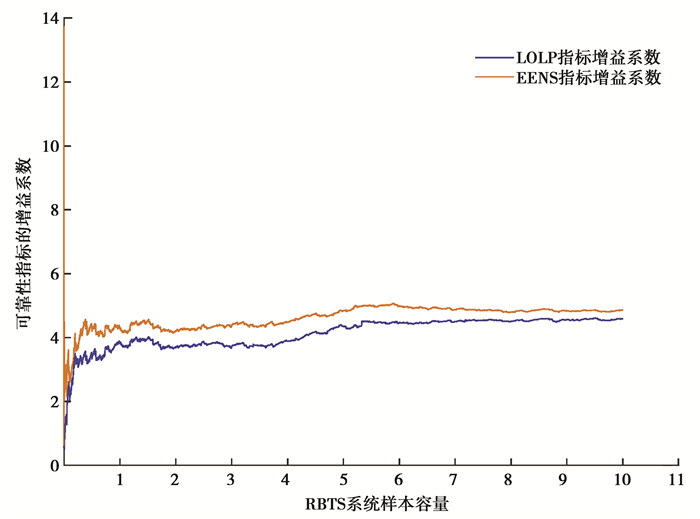
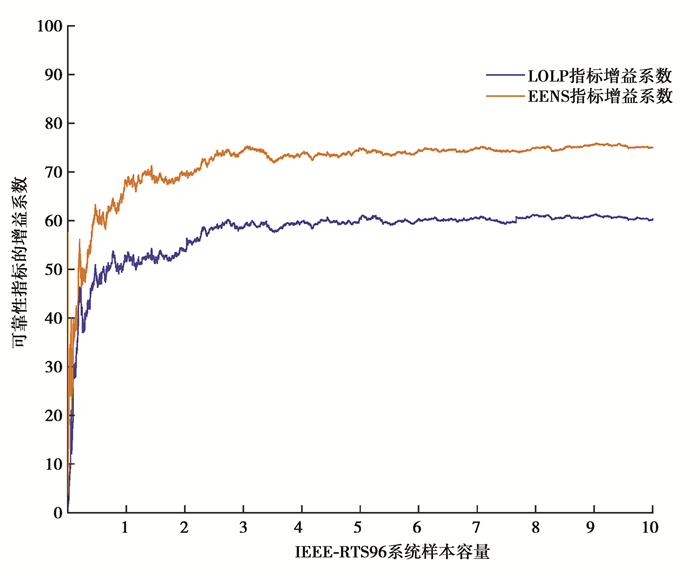
分别采用缺供电量和失负荷概率指标的方差系数来衡量可靠性评估结果的准确性,采用固定抽样样本数,图 3~5给出了以基于潮流灵敏度的常规启发式负荷削减模型为参考,本文模型的增益系数变化过程。可见本文模型效率更好,原因如下:
|
图 3 RBTS系统各项指标的增益系数 Figure 3 gain factor of each index for RBTS system |
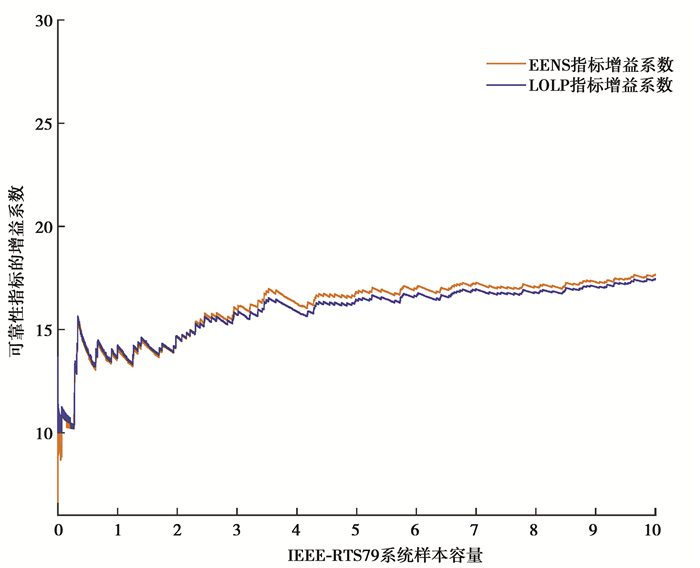
|
图 4 IEEE-79系统各项指标的对数增益 Figure 4 gain factor of each index for IEEE-79 system |
|
图 5 IEEE-96系统指标的增益系数 Figure 5 logarithmic index gain for IEEE-96 system |
① 潮流灵敏度矩阵求解算法不同:基于潮流灵敏度的常规启发式负荷削减模型,在每个故障系统状态下的潮流灵敏度矩阵计算均涉及大规模矩阵求逆,计算量较大;而本文模型在潮流灵敏度矩阵求解时利用了基态下的潮流灵敏度信息,进行求逆计算的矩阵阶数大大降低。
② 节点注入功率调节量调整方式不同:基于潮流灵敏度的常规启发式负荷削减模型按潮流灵敏度绝对值进行逐个调节,每次只针对一个控制节点;本文模型根据反向等量配对原理进行调节,每次调节包括两个控制节点,调节效率更高。
③ 节点注入功率调节量的计算不同:基于潮流灵敏度的常规启发式负荷削减模型,其控制节点注入功率调节量的计算仅考虑节点自身调节能力和为消除支路过载所需要的调节量约束,易导致正常支路在调节过程中反复出现过载,因此,需要进行反复潮流校验;而本文模型基于潮流灵敏度与反向等量配对原理,配对节点组的注入功率调节量考虑了调节过程对正常支路潮流的影响,故不会在调节过程中引起正常支路过载,避免了潮流校验过程。
6 结语笔者提出一种可快速评估电网可靠性的启发式负荷削减模型。首先在现有潮流灵敏度求解基础上,借助基态潮流灵敏度矩阵信息,根据Wood bury矩阵变换推导了故障状态下潮流灵敏度矩阵的快速计算解析表达式。其次,给出了控制节点的筛选规则,为避免启发式调节过程引起正常支路反复过载的拉锯现象,计及调节过程对正常支路的影响,给出了配对节点组功率调节量的修正公式,避免了常规启发式模型的潮流校验过程,一定程度上提高了校正调节的有效性和快速性。
| [1] | Billinton R, Li W Y. Reliability assessment of electric power systems using Monte Carlo methods[M]. New York: Plenum Press, 1994. |
| [2] |
李文沅. 电力系统风险评估: 模型、方法和应用[M]. 周家启, 卢继平, 胡小正, 等, 译. 北京: 科学出版社, 2006: 1-9. LI Wenyuan. Risk assessment of power system models, methods, and applications[M]. Translated by Zhou Jiaqi, Lu Jiping, Hu Xiaozheng, et al. Beijing: Science Press, 2006: 1-9(in Chinese) |
| [3] | Billinton R, Allan R N. Reliability evaluation of power systems[M]. London: Pitman Publishing Limited, 1984. |
| [4] | Merlin A, Oger P. Application of variance reducing technique to a Monte Carlo simulation model of power transmission system[C]//Workshop Proceedings on Power System Reliability, Research Needs and Priorities, 1978. |
| [5] | Akbari M, Khazaee P, Sabetghadam P K, et al. Failure modes and effects analysis (FMEA) for power transformers[C]// Power Transmission & Distribution Research Center Niroo Research Institute (NRI) Tehran, Iran. 28th international Power System Conference, Iran, November 2013. |
| [6] | Merlin A, Oger P. Application of variance reducing technique to a Monte Carlo simulation model of power transmission system[C]//Workshop Proceedings on Power System Reliability, Research Needs and Priorities, 1978. |
| [7] | Sun R, Singh C, Cheng L, et al. Short-term reliability evaluation using control variable based dagger sampling method[J]. Electric Power Systems Research, 2010, 80(6): 682–689. DOI:10.1016/j.epsr.2009.10.037 |
| [8] |
石文辉, 别朝红, 王锡凡.
大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J]. 中国电机工程学报, 2005, 25(4): 40–45.
SHI Wenhui, BIE Zhaohong, WANG Xifan. The applications of Markov Chain Monte Carlo in Large-scale System Reliability Evaluation[J]. Proceedings of the CSEE, 2005, 25(4): 40–45. (in Chinese) |
| [9] | Pickles J H, Russell I H. Importance sampling for power system security assessment[C]//Probabilistic Methods Applied to Electric Power Systems. 1991. Third International Conference On 3-5 Jul 1991 Page(s): 47-52. |
| [10] | Gonzalez-Fernandez R A, Leite da Silva A M, Resende L C, et al. Composite systems reliability evaluation based on Monte Carlo simulation and cross-entropy methods[J]. Power Systems, IEEE Transactions on, 2013, 28(4): 4598–4606. DOI:10.1109/TPWRS.2013.2267154 |
| [11] |
肖炎, 郭永基, 席勇健.
一种评估大规模电力系统可靠性的新算法[J]. 清华大学学报(自然科学版), 1999, 39(1): 12–15.
XIAO Yan, GUO Yongji, XI Jianyong. New algorithm for large power reliability evaluation[J]. Journal of Tsinghua University(Science and Technology), 1999, 39(1): 12–15. (in Chinese) |
| [12] |
赵渊, 周家启, 周念成.
发输电系统可靠性评估的启发式就近负荷削减模型[J]. 电网技术, 2008(23): 34–39.
ZHAO Yuan, ZHOU Jiaqi, ZHOU Niancheng. A Heuristic Approach to Local Load Shedding Scheme for Reliability Assessment of Composite Generation and Transmission System[J]. Power System Technology, 2008(23): 34–39. (in Chinese) |
| [13] | Zaborsky J, Whang K W, Prasad K. Fast contingency evaluation using concentric relaxation[J]. IEEE Trans on Power Apparatus and Systems, 1980, 99(1): 28–36. |
| [14] |
赵渊, 周家启, 谢开贵.
基于网流规划的发输电组合系统可靠性评估模型研究[J]. 电网技术, 2003, 27(10): 21–24.
ZHAO Yuan, ZHOU Jiaqi, XIE Kaigui. Study on reliability assessment model of composite generation and transmission system based on network flow programming[J]. Power System Technology, 2003, 27(10): 21–24. DOI:10.3321/j.issn:1000-3673.2003.10.005 (in Chinese) |
| [15] |
王韶, 周家启.
基于函数型连接神经网络的发输电系统可靠性评估研究[J]. 中国电机工程学报, 2004, 24(9): 142–146.
WANG Shao, ZHOU Jiaqi. Reliability assessment of composite generation and transmission system based on functioned link neural network[J]. Proceedings of the CSEE, 2004, 24(9): 142–146. (in Chinese) |
| [16] |
徐岩, 郅静.
基于直流潮流和虚拟母线的多控制节点防连锁过载跳闸策略[J]. 电工技术学报, 2015, 30(13): 77–86.
XU Yan, ZHI Jing. A Multi Control-node Emergency Control Strategy Based on DC Power Flow and Virtual Bus[J]. Transactions of china electro technical society, 2015, 30(13): 77–86. DOI:10.3969/j.issn.1000-6753.2015.13.011 (in Chinese) |
| [17] |
张保会, 姚峰, 周德才.
输电断面安全性保护及其关键技术研究[J]. 中国电机工程学报, 2006, 26(21): 1–7.
ZHANG Baohui, YAO Feng, ZHOU Deicai. Study on Security Protection of Transmission Section and Its Key Technologies[J]. Proceedings of the CSEE, 2006, 26(21): 1–7. DOI:10.3321/j.issn:0258-8013.2006.21.001 (in Chinese) |
| [18] |
程临燕, 张保会, 郝治国, 等.
基于综合灵敏度分析的快速控制算法研究[J]. 电力自动化设备, 2009, 29(4): 46–49.
HENG Linyan, ZHANG Baohui, HAO Zhiguo, et al. Fast control algorithm based on integrative sensitivity analysis[J]. Electric Power Automation Equipment, 2009, 29(4): 46–49. (in Chinese) |
| [19] |
邓佑满, 黎辉, .
电力系统有功安全校正策略的反向等量配对调整法[J]. 电力系统自动化, 1999, 23(18): 5–8.
DENG Youman, LI Hui, Zhang Boming, et al. Adjustment of equal and opposite quantities in pairs for strategy of active power secturity correction of power systems[J]. Automation of Electric Power Systems, 1999, 23(18): 5–8. DOI:10.3321/j.issn:1000-1026.1999.18.002 (in Chinese) |
| [20] |
赵晋泉, 江晓东, 张伯明.
一种基于连续线性规划技术的在线静态安全校正算法[J]. 电网技术, 2003, 27(10): 21–24.
ZHAO Jinquan, CHIANG HsiaoDong, ZHANG Boming. A successive linear programming based on-line static security corrective control approach[J]. Power System Technology, 2003, 27(10): 21–24. DOI:10.3321/j.issn:1000-3673.2003.10.005 (in Chinese) |
| [21] | Sherman J, Morrison W J. Adjustment of an inverse matrix corresponding to a change in one element of a given matrix[J]. Annals of Mathematical Statistics, 1950, 21(1): 124–127. DOI:10.1214/aoms/1177729893 |
| [22] | Billinton R, Kumar S N, Chowdhury N, et al. A reliability test system for educational purposes-basic data[J]. IEEE Trans. on Power Systems, 1989, 4(3): 1238–1244. DOI:10.1109/59.32623 |
| [23] | IEEE Subcommittee. The IEEE reliability test system 1996[J]. IEEE Trans. on Power Systems, 1999, 14(3): 1010–1020. DOI:10.1109/59.780914 |
 2018, Vol. 41
2018, Vol. 41

