大数据时代的本质是在数据处理的基础上实现硬件智能化,其目标是真正实现人与物的智能交互,甚至物与物的智能交互,建立一个全新的生产模式及产业结构。现在全球数据量呈现井喷式的增长,最近几年数据量的增长速度都是保持在50%以上,而当前数据总量的80%都是最近两年产生。如此庞大的数据不仅仅对现有计算机的计算能力提出了挑战,也让传统的数据处理办法显得捉襟见肘,分类相关算法在这样的背景下应运而生。
分类算法是解决分类问题的方法,是数据挖掘、机器学习和模式识别中一个重要的研究领域。常见的分类算法有决策树分类、KNN算法、支持向量机、朴素贝叶斯、随机森林算法等。随机森林算法是Breiman L[1]于2001年提出的一个可处理高维度和非线性样本的分类器组合模型,并在众多领域得到了广泛应用。
在随机森林算法发展的过程中,算法对非平衡数据分类时性能不足缺陷逐渐地显露出来。黄衍等人[2]对比非平衡分类问题上随机森林和支持向量机的性能,随机森林算法在非平衡分类数据的处理显著逊色于支持向量机的结论。
现有国内外对随机森林算法改进方法大致可以分为3类:①将新的理论引入随机森林算法,随机森林算法本身就是Breriman将自己的Bagging算法[3]与Tin Kam Ho的Random Subaspace算法[4]结合得到的算法,很多学者致力于将其他算法与随机森林算法结合来提升性能,例如Gall[5],Ishwaran等人[6]。②数据预处理融入随机森林算法、针对随机森林算法处理非平衡数据时性能不足的问题,将数据预处理后再利用随机森林算法分类,可有效提升随机森林对非平衡数据的敏感度。例如,吴琼[7]、杜军[8]等人。③对随机森林算法构建过程进行优化。在构建随机森林算法的过程中,增加决策树的强度可以有效提升随机森林算法的性能,例如雍凯等人[9]为属性进行权重评估,在生成决策树时优先选择权重大的属性借此提升单个决策树的分类性能。
1 随机森林算法处理非平衡数据数据集多而复杂造成了实际中同一种算法处理不同数据集时的性能波动。为了高效处理数据集,客观衡量算法的性能。根据数据集自身的某一个特点或者某一类特点对数据进行分类成为一种行之有效的方法。非平衡数据就是基于这一背景下诞生的产物。
当一个数据集呈现出不等分布的特性时这些数据集叫做非平衡数据集。非平衡数据集是指数据集中某一类的样本数量明显少于其他类样本的数目,其中占数量最多的一类样本被称为多数类(正类),而占数量最少的一类则称为少数类(负类)。如果数据集中某一类的数量远远大于另一类的数量时,这类数据集叫做类间不平衡。现实生活中非平衡数据并不少见,例如疾病监测,生病人数往往远远少于健康的人数,例如网络攻击监测,攻击行为数远远少于正常访问,因此,非平衡数据研究具有重要的应用价值和理论意义。
为了方便表述有如下定义:
① 假设样本集S中样本数为|S|=m。
② S={(xi, yi)}, i=1, …, m,这里xi满足xi∈X,而X是维度为n的空间,X={f1, f2, …, fn},并且yi∈Y={1, …, C}是样本的特征值。
③ Smin是少数类样本,Smax是多数类样本,满足Smin∩Smax={∅}并且Smin∩Smax={S}。
④ R为数据集不平衡度,
由于非平衡数据本身的特殊性,所以非平衡数据并不可平衡数据,主要依靠训练精度作为标准来评价分类性能。针对上述问题,建立非平衡数据分类精度混淆矩阵:
其中Pos为正类样本,Neg为负类样本;
N=Pos+Neg是全体学习样本。
TP(true positive)和TN(true negative)分别表示被分类正确的多数类样本和被分类正确的少数类样本。
FP(false positive)和FN(false negative)分别表示被分类错误的多数类样本和被分类错误的少数类样本。
| 表 1 混淆矩阵 Table 1 Confusion matrix |
各个指标的具体计算公式如下:
| $ TP\;rate = TP/Pos = TP/\left( {TP + FN} \right), $ | (1) |
| $ FP\;rate = FP/Neg = FP/\left( {TN + FP} \right), $ | (2) |
精度为
| $ {\rm{accuracy}} = \left( {TP + TN} \right)/{\rm{N,}} $ | (3) |
查准率为
| $ {\rm{precision}} = TP/\left( {TP + FP} \right), $ | (4) |
查全率为
| $ {\rm{recall}} = TP\;rate。$ | (5) |
根据以上定义考虑非平衡数据分类器分类性能时要考虑精度(accuracy),查准率(precision)以及查全率(recall)。对于一个非平衡数据分类器而言这些指标越高,分类器性能越好。
1.2 真正类趋势图为了直观地比较算法之间性能的差异还可以通过TP/FP散点对比图,也就是算法把正类数据分类正确的程度。TP/FP散点对比图中以FP rate为横轴,以TP rate为纵轴。上图中每一个黑点都代表了一个分类器。
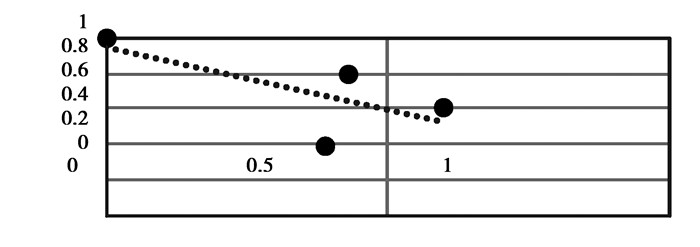
|
图 1 TP/FP散点对比图 Figure 1 Comparison of TP/FP |
点越靠近左上角分类器性能越好,也就是代表分类器的点与(0,1)距离越小分类性能越好,在实际应用中FP rate越小,TP rate越大分类性能越好。
随机森林算法中决策树的数量与分类性能成正相关,因为决策树的数量越多相当于投票的专家越多,分类结果越好,相应的时间复杂度和空间复杂度就会增加,在到达一定的数量时分类性能达到最佳。刘敏等[10]利用UCI数据集对随机森林算法中决策树的数量与数据集的关系进行了实验分析,得出当决策树的数量为100时大部分的分类性能最好。当决策树数目不同得到的ROC点也不同,将这些点连起来,如果一个分类器的ROC散点图总在另外一个分类器左上方,可以说在ROC散点图左上方的那条分类性能较好。
接下来会用两种评价来对比改进后的随机森林算法与原始随机森林算法的区别。
2 处理非平衡数据分类的方法 2.1 数据预处理,过抽样与欠抽样非平衡数据的处理方法可以总结为过抽样和欠抽样,也就是通过重抽样,以及去噪声和冗余数据等方法来降低数据不平衡度
常见的过抽样方法代表是由Chawla等[11]提出的SMOTE技术,其核心思想是通过插值在少数类样本插入人造样本。Han等[12]在SMOTE方式的基础上提出了Borderline-SMOTE技术,通过在适当的地方插值,从而保证增加的样本是有意义的。
而欠抽样技术常见的有Tomek link、一致子集(consistent subset)、编辑技术(Wilson’s editing)editing)以及单边选择(one-sided selection)等[13-14]。Barandela等[15]整理对比了上述算法的优缺点。另外Dehmeshki等[16]提出了数据过滤技术,根据构造的规则将发现数据中的安全区,将安全区中的样本点舍弃不用,这种方法本质上也是一种欠抽样技术。
所有的欠抽样技术或者过抽样技术都取得了很好的效果,因此,在处理一个非平衡数据问题时人们常常两种技术同时使用。
2.2 算法层面的改进改进现有算法对非平衡数据的敏感性[10]和根据非平衡数据的特点设计新的算法都是处理非平衡数据分类的方法。
例如:考虑误分代价[17-19]的Cost-sensitive学习。
Step1 建立代价矩阵C,其中C(i, j)表示,将类标号为j的样本误分为类i的代价,一般假设C(i, i)=0。
Step2 最小化条件风险[17]。
| $ R\left( {i\left| x \right.} \right) = \sum\limits_j {P\left( {j\left| x \right.} \right)C\left( {i,j} \right)} 。$ | (6) |
这里的R(i|x)表示将x分为i类的平均代价。对x来说应该选择k=argminR(i|x)作为其类别号。
Step3 假设j是少数类时,一般情况下选择C(i, j)>C(j, i)的情况。一方面这样降低少数类的误分代价,在实际情况下少数类被错分的情况造成的后果往往比多数类被错分造成的结果严重得多,另一方面误分代价将分类边界向多数类偏移,可以提升少数类的分类精度。
2.3 组合方法组合方法的主要思想在于将多个分类器组合成一个分类器,以提高分类性能。其中,提升是被广泛使用的技术。通过提升,多个弱分类器可以组合成一个强分类器。AdaBoost是采用提升技术算法的代表。在该算法中,最终得到的分类器是多个弱分类器的线性组合形式:
| $ H\left( x \right) = sign\left( {\sum {{a_t}{H_t}\left( x \right)} } \right)。$ | (7) |
抽样方法的最终目的都是期望通过抽样得到的样本尽可能靠近总体。随机森林算法使用的Bootstrap算法是随机森林分类算法随机性的保证。Bootstrap重抽样方法每次抽取总体的2/3作为一个训练样本,不断地重复这一个抽取动作,以期望用一系列大小为原训练样本2/3的训练样本搭建出一个空间,通过这个空间达到无限接近总体的目的。
这样做显然具有很高的合理性,因为当抽样的数目越多,搭建出来空间的特点越接近整体的特点。当抽样的次数达到一定的程度后,是可以无限趋近于原样本的。但这样做具有很强的随机性,具体体现在以下3个方面:
1) 每一次抽样的样本彼此不同,相互独立。
2) 每一组抽样结果都是唯一的,每再抽一次样都会得到一组全新的抽样结果。
3) 训练样本不同,不同的训练样本训练出来的决策树显然也不会相同,因此,同一组数据,会训练出很多不同的随机森林。
但是Bootstrap的随机性会加剧抽样子集的非平衡性问题。非平衡数据之所以难处理,从本质上来说是因为数据分配不均匀造成,从非平衡系数R的角度可以把Bootstrap重抽样的结果分成3种情况:
1) 训练子集中没有少数类,训练子集中非平衡系数R′无法计算。
2) 训练子集中少数类很少,训练子集中非平衡系数R′大于原非平衡系数R。
3) 训练子集中少数类样本充足,训练子集中非平衡系数R′小于等于原非平衡系数R。
由于Bootstrap抽取每一个子集时是简单随机抽样,所以上述3种情况出现的概率是相同的。但是第1种和第2种情况抽样得到的子集对于处理非平衡问题没有帮助的,可以称之为无效子集。无效子集的存在会导致构建出来可以代替整体的子集空间所需要的子集数量增加。这样一方面增加了抽样成本,另一方面在用这些无效子集训练出来的决策树效率不仅低下,而且会干扰最终的投票结果。
3.1.2 添加约束条件的Bootstrap重抽样提出了一种增加约束条件的Bootstrap重抽样算法,对抽样结果进行筛选,剔除抽样结果中的无效子集,从而保证得到的训练子集中非平衡系数R′小于等于原非平衡系数。
改进后的随机森林算法的Bootstrap重抽样的工作步骤如下:
Step1 从数据S中抽取2/3的数据样本,记录观测值再放回。
Step2 从数据S中抽取数据时设定代价,保证抽样得到的数据集非平衡度不超过原数据集:
| $ \left| {\frac{{{{S'}_{\max }}}}{{{{S'}_{\min }}}}} \right| \le R, $ | (8) |
S′max为抽样后的多数类数据集,S′min为抽样后的少数类数据集,其中
| $ \left| {{{S'}_{\max }} \cup {{S'}_{\min }}} \right| = \frac{2}{3}\left| S \right|。$ | (9) |
Step3 如果抽样得到的数据集满足step2中的条件则重复step1,总计重复c次,c为拟构造决策数的数量。
实验证明上述改进的抽样算法是可以有效地提升原算法对非平衡数据的敏感性,但是增加限制条件毫无疑问地增加了训练成本。即使训练的复杂度并不会影响分类器的复杂度,但毕竟每次都要计算抽样出的训练集的非平衡系数R′,这确实增加了训练成本。
对于一个非平衡系数为R的数据集,在去除单位后,可以令
| $ \left| {{S_{\min }}} \right| = 1\& \left| {{S_{\max }}} \right| = R, $ | (10) |
这样
| $ \left| S \right| = R + 1。$ | (11) |
那么相应抽样后的少数类样本数量|S′min|∈[0, 1], 根据公式(8),有以下的推导:
| $ \left| {\frac{{{{S'}_{\max }}}}{{{{S'}_{\min }}}}} \right| = R' \le R \Rightarrow \frac{{\frac{2}{3}\left( {R + 1} \right) - {{S'}_{\min }}}}{{{{S'}_{\min }}}} \le R \Rightarrow \\ {{S'}_{\min }}R \ge \frac{2}{3}R + \frac{2}{3} - {{S'}_{\min }} \Rightarrow \left( {{{S'}_{\min }} - \frac{2}{3}} \right){\rm{R}} \ge \left( {\frac{2}{3} - {{S'}_{\min }}} \right), $ |
因此,有且只有
| $ {{S'}_{\min }} \ge \frac{2}{3}{S_{\min }}。$ | (12) |
式(8)才成立。从而上述改进的Bootstrap重抽样算法的约束条件也可以改为保证每次抽到的少数类样本至少要占总体少数类样本的2/3。
3.2 加权的随机森林算法 3.2.1 决策树分类性能差异分析传统随机森林算法使用的基分类器是CART决策树,该决策树使用的是随机选取属性进行分裂。CART算法采取的是最小基尼系数分割。具体分割方法如下:
| $ Gin{i_{{\rm{split}}}}{\rm{S}} = \left| {\frac{{{S_1}}}{S}} \right|Gini\left( {{S_1}} \right) + \left| {\frac{{{S_2}}}{S}} \right|Gini\left( {{S_2}} \right), $ |
其中:
| $ Gini\left( S \right) = 1 - \sum\limits_{i = 1}^m {P_i^2} 。$ |
在一个非平衡系数为R′R′二类非平衡数据问题中
| $ \sum\limits_{i = 1}^m {P_i^2} = {\left( {\frac{1}{{R' + 1}}} \right)^2} + {\left( {\frac{{R'}}{{R' + 1}}} \right)^2}Gini\left( S \right) = 1 - \sum\limits_{i = 1}^m {P_i^2} = 1 - \left\{ {{{\left( {\frac{1}{{R' + 1}}} \right)}^2} + {{\left( {\frac{{R'}}{{R' + 1}}} \right)}^2}} \right\}, $ |
| $ Gin{i_{{\rm{split}}}}S = \left| {\frac{{{S_1}}}{S}} \right|\left\{ {1 - \left( {{{\left( {\frac{1}{{{{R'}_1} + 1}}} \right)}^2} + {{\left( {\frac{{{{R'}_1}}}{{{{R'}_1} + 1}}} \right)}^2}} \right)} \right\} +\\ \left| {\frac{{{S_2}}}{S}} \right|\left\{ {1 - \left( {{{\left( {\frac{1}{{{{R'}_2} + 1}}} \right)}^2} + {{\left( {\frac{{{{R'}_2}}}{{{{R'}_2} + 1}}} \right)}^2}} \right)} \right\}, $ |
在理想的基础上S1/S2=R,这意味着多数类和少数类被完全分开。
| $ Gin{i_{{\rm{split}}}}S = \left| {\frac{R}{{R + 1}}} \right|\left\{ {1 - \left( {{{\left( {\frac{1}{{{{R'}_1} + 1}}} \right)}^2} + {{\left( {\frac{{{{R'}_1}}}{{{{R'}_1} + 1}}} \right)}^2}} \right)} \right\} +\\ \left| {\frac{1}{{R + 1}}} \right|\left\{ {1 - \left( {{{\left( {\frac{1}{{{{R'}_2} + 1}}} \right)}^2} + {{\left( {\frac{{{{R'}_2}}}{{{{R'}_2} + 1}}} \right)}^2}} \right)} \right\}, $ |
| $ Gin{i_{{\rm{split}}}}S = \left| {\frac{R}{{R + 1}}} \right|\left\{ {1 - \left( {\frac{{1 + {{R'}_1}^2}}{{{{R'}_1}^2 + 2{{R'}_1} + 1}}} \right)} \right\} + \left| {\frac{1}{{R + 1}}} \right|\left\{ {1 - \left( {\frac{{1 + {{R'}_2}^2}}{{{{R'}_2}^2 + 2{{R'}_2} + 1}}} \right)} \right\}。$ |
这样在对于非平衡数据求最小基尼系数时就可以转换为一个关于非平衡系数的问题。目标节点S1是多数类样本,S2是少数类样本。根据非平衡数据节点尽量纯的原则,R′1一定满足1<R<R′1。R′2一定满足0<R′2<1。那么如何使GinisplitS最小,就是R′1趋近于R,R′2趋近于0,因此,构造决策树的数据集的非平衡系数R越靠近1越能纯净地把正负类分开。
3.2.2 加权的随机森林分类算法Bootstrap重抽样由Bootstrap重抽样可知,训练CART决策树的数据集是随机产生的,因此,这些数据集的非平衡系数是不同的,这就导致由这些数据集训练出来的决策树的能力是有差异的。但是在随机森林算法中,这些决策树并不会区别对待,分类性能差的决策树和分类性能好的决策树拥有相同的投票权,这显然是不合理的。如果能对这些决策树进行区别对待,提升性能好的决策树的话语权无疑可以提升随机森林算法的投票效率。在这一基础上提出了一种基于非平衡系数的加权随机森林算法。具体实现步骤如下:
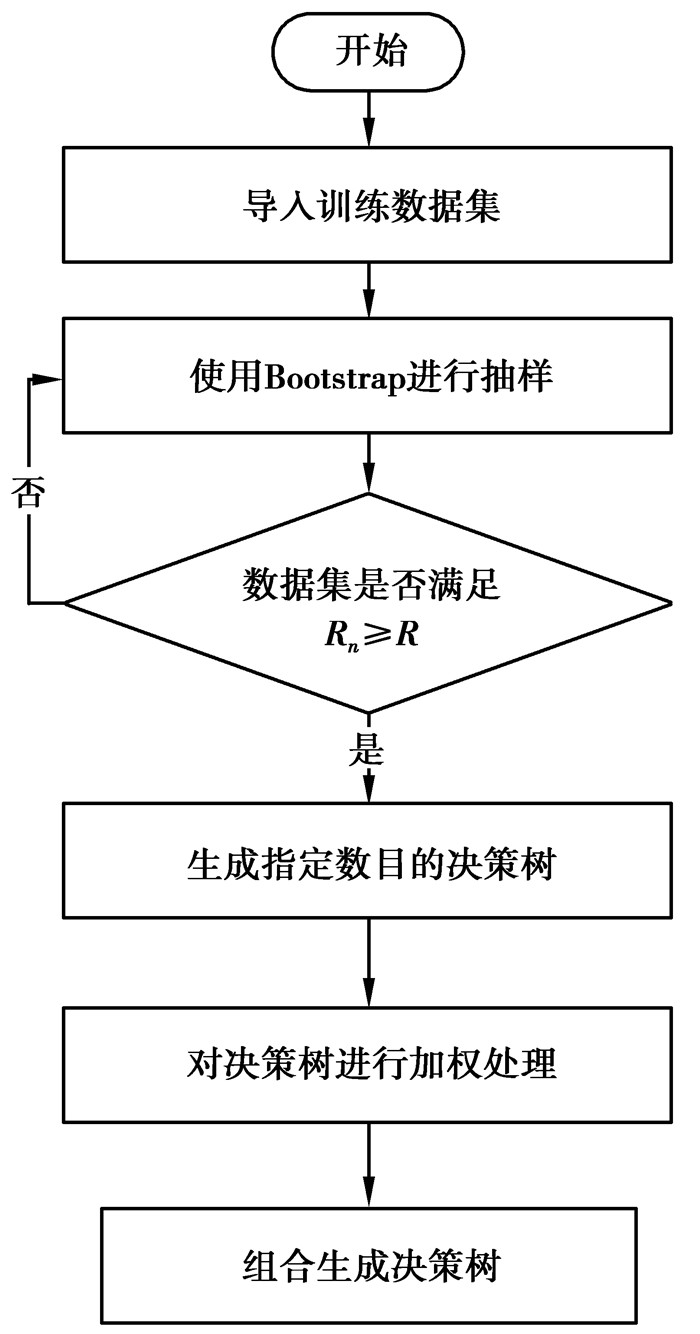
|
图 2 改进后的算法流程图 Figure 2 The improved random forests algorithm flowchart |
假设所有决策树原始投票权重为1,计算每棵树的权重方式为每棵树自身数据集的Rn比上所有抽样后数据集的平均数,权重函数如下:
| $ C\left( n \right) = \frac{{{R_n}}}{{\sum\nolimits_1^N {{R_n}/N} }}, $ | (13) |
把构造好的决策树每一个决策树的投票权重设定为1,这对随机森林算法决定一个样本类别是没有影响的。除以平均数是为了降低某些非平衡度高的数据集对结果有过分的影响力。
例如:对于一颗决策树来说,该决策树的非平衡度Rn为9而所有抽样数据集非平衡度的平均数为10,该决策树的投票权重为9/10×1=0.9。
4 算法合理性分析 4.1 实验设计笔者提出了2种改进,一是改进的Bootstrap重抽样,二是在第1种改进的基础上利用非平衡系数对决策树进行加权后投票,为了可以清晰地证明算法改进的有效性。
每种算法分别比较决策树的数量N在10,20,…,90,100时的分类精度以及ROC曲线图。由于随机森林算法处理非平衡数据时的不稳定性,所以为了保证结果的稳定性,每次实验都重复100次取平均数。
实验数据采用来自KEEL [20],数据集仓库中9个非平衡二类分类数据,这些数据集的不平衡系数(imbalance ratios,R) [21]分布在1.5~9范围内。表 2描述了Dataset为数据集名,total为数据集总样本数,dim为维数,R为不平衡系数。
| 表 2 实验数据集 Table 2 Experimental data sets |
从图 3可以清晰地看出改进后的算法相比于原算法对herbeman的分类精度有明显提升,其中在改进的Bootstrap重抽样算法基础上进行的加权随机森林算法可以进一步提升精度。
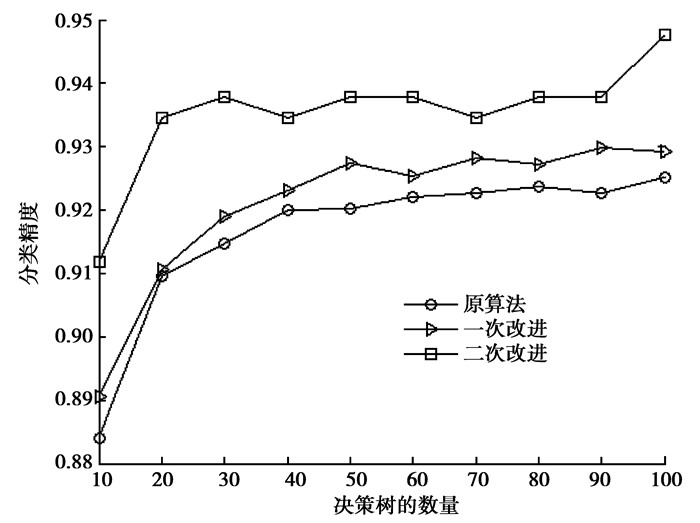
|
图 3 精度对比图 Figure 3 Comparison of accuracy |
从图 4可以发现改进的算法不仅可以提升分类精度,更多的正类被正确地分到了目标类当中。
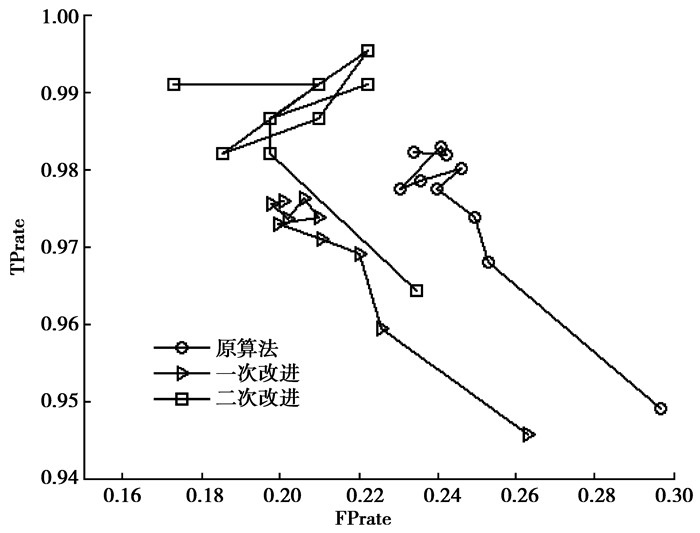
|
图 4 TP/FP散点对比图 Figure 4 Comparison of TP/FP |
实验表明,改进后的算法不仅对herbman分类有所提升,也可以对其他实验数据的分类性能也有显著的提升。
由表 3不难看出,在进行了算法改进后,随机森林算法拥有相同的决策树数目时,第一次改进和第二次改进都可以提升算法的分类精度,其中在一次改进基础上进行的二次改进分类精度也是优于仅仅进行一次改进的分类精度。
| 表 3 部分实验结果 Table 3 Part of the experimental results |
针对随机森林处理非平衡数据性能不足的问题,在原算法的基础上,提出了2种改进。改进的Bootstrap重抽样和加权的随机森林算法。实验表明2种改进均可以有效提升随机森林算法处理非平衡数据的性能,这一提升在决策树数量不足的情况下效果尤其明显。
| [1] | Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5–32. DOI:10.1023/A:1010933404324 |
| [2] |
黄衍, 查伟雄.
随机森林与支持向量机分类性能比较[J]. 软件, 2012(6): 107–110.
HUANG Yan, ZHA Weixiong. Comparison on classification performance between random forests and support vector machine[J]. Software, 2012(6): 107–110. (in Chinese) |
| [3] | Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123–140. |
| [4] | Ho T K. Random Decision forests[C]// International Conference on Document Analysis and Recognition. Washington, DC: IEEE Computer Society, 1995. |
| [5] | Gall J, Lempitsky V. Class-specific Hough forests for object detection[C]// Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Los Alamitos: IEEE Computer Society Press, 2009. |
| [6] | Ishwaran H, Kogalur U B, Blackstone E H, et al. Random survival forests[J]. Journal of Thoracic Oncology Official Publication of the International Association for the Study of Lung Cancer, 2011, 6(12): 1974–1975. |
| [7] |
吴琼, 李运田, 郑献卫.
面向非平衡训练集分类的随机森林算法优化[J]. 工业控制计算机, 2013, 26(7): 89–90.
WU Qiong, LI Yuntian, Zheng Xianwei. Optimized random forests algorithm for imbalanced training sets[J]. Industrial Control Computer, 2013, 26(7): 89–90. (in Chinese) |
| [8] |
杜均. 代价敏感学习及其应用[D]. 武汉: 中国地质大学, 2009. DU jun. Cost sensitive learning and its application[D]. China University of Geosciences, 2009. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1661819 |
| [9] |
雍凯. 随机森林的特征选择和模型优化算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2008. YONG Kai. Research on feature selection and model optinization of random forest[D]. Harbin: Harbin Institute of Technology, 2008. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D255976 |
| [10] |
刘敏, 郎荣玲, 曹永斌.
随机森林中树的数量[J]. 计算机工程与应用, 2015, 51(5): 126–131.
LIU Min, LANG Rongling, CAO Yongbin. Number of trees in random forest[J]. Computer Engineering and Applications, 2015, 51(5): 126–131. (in Chinese) |
| [11] | Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2011, 16(1): 321–357. |
| [12] | Han H, Wang W Y, Mao B H. Bordeline-SMOTE: A new over-sampling method in imbalanced data sets learning[J]. Lecture Notes in Computer Science, 2005, 3644(5): 878–887. |
| [13] | Batista G E A P A, Prati R C, Monard M C. A study of the behavior of several methods for balancing machine learning training data[J]. Acm Sigkdd Explorations Newsletter, 2004, 6(1): 20–29. DOI:10.1145/1007730 |
| [14] | Kubat M, Matwin S. Addressing the curse of imbalanced training sets: One-sided selection[C]// International Conference on Machine Learning, 2000. http://www.researchgate.net/publication/2624358_Addressing_the_Curse_of_Imbalanced_Training_Sets_One-Sided_Selection |
| [15] | Barandela R, Valdovinos R M, Sánchez J S, et al. The imbalanced training sample problem: Under or over sampling[J]. Lecture Notes in Computer Science, 2004. |
| [16] | Dehmeshki J, KarakÖY M, Casique M V. A rule-based scheme for filtering examples from majority class in an imbalanced training set[C]// International Conference on Machine Learning and Data Mining in Pattern Recognition. Verlag: Springer, 2003. http://www.researchgate.net/publication/221506274_A_Rule-Based_Scheme_for |
| [17] | Elkan C. The foundations of cost-sensitive learning[C]// Proc of the 17th International Joint Conference on Artificial Intelligence(IJCAI01). Washington DC: University of California, San Diego, 2001. |
| [18] | Domingos P. Metacost: A general method for making classifiers cost-sensitive[C]// ACM Sigkdd International Conference on Knowledge Discovery and Data Mining. ACM, 2002. http://dl.acm.org/citation.cfm?id=312220 |
| [19] | Fan W, Stolfo S J, Zhang J, et al. AdaCost: Misclassification cost-sensitive boosing[C]// Sixteenth International Conference on Machine Learning. Morgan Kaufmann Publishers Inc. 1999. http://dl.acm.org/citation.cfm?id=657651 |
| [20] | Alcalá-Fdez J, FernáNdez A, Luengo J, et al. KEEL data-mining software tool: Data set repository, integration of algorithms and experimental analysis framework[J]. Jaurnal of Multiple-Valued Logic & Soft Computing, 2011, 17: 255–287. |
| [21] |
彭立志. 基于机器学习的流量识别关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. PENG Lizhi. Research on key technologies of machine learning based traffic identification[D]. Harbin: Harbin Institute of Technology, 2015. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D751862 |
 2018, Vol. 41
2018, Vol. 41


