b. 宝山钢铁股份有限公司研究院, 上海 201900
b. Research Institute, Baoshan Iron & Steel Co., Ltd., Shanghai 201900, P. R. China
在热轧及厚板轧制过程中,轧制力预测是过程控制模型的核心,其精度不仅影响产品的厚度精度,保证轧制过程的稳定进行,而且对板形控制,设备保护等均有重要意义。传统计算轧制力的变形抗力模型,考虑了材料成分的影响,变形条件包括变形程度、变形速率和变形温度的影响[1-4]。然而,对于部分碳含量较高的钢种,其奥氏体区,铁素体区及两相区的流变应力随变形温度的变化较为平滑,一个变形抗力模型就能大致预测整个高温过程流变应力。但对于另一部分材料而言,流变应力在奥氏体区,铁素体区及两相区的变化较大,往往在两相区流变应力呈现出较大的降幅,此时则不能用单一的变形抗力模型来预测[5-11]。这种情况下,往往采取分段函数的方法来分别计算奥氏体区、铁素体区及两相区的变形抗力[12-13]。但这种方法需要一个前提,即能预测出试样在该变形条件下的铁素体相变开始温度。
关于铁素体相变开始温度,之前也有不少学者通过热膨胀的方法确定,除了考虑主要合金元素,部分还考虑了冷却速率和钢板规格[14-15]。本研究通过分析所研究钢种的实测流变应力,提取流变应力特征值,包括两相区流变应力的降幅,以及铁素体相变开始温度,建立模型用以描述主要化学成分对这两个特征值的影响。
1 试验材料与方法本研究所用钢种包含10种不同的化学成分,如表 1所示。其中钢种BA为常规Q235的成分,A1,A2和A3在BA的基础上调整了C的成分。类似地,B1、B2和B3为BA的基础上调整了Si的成分,C1、C2和C3为BA的基础上调整了Mn的成分。
| 表 1 试验钢种的化学成分/% Table 1 The chemical composition of the studied steels/% |
在实验室的真空感应炉中铸造上述成分的铸锭,然后直接锻造成长方体试样,锻造后的试样被进行了热轧。为了保证试样的成分均匀,热轧后的试样变形后直接淬火至室温。最后,从热轧板上加工出直径8 mm,高度12 mm的圆柱形试样。
试验在Thermomaster-z热模拟实验机上进行。如图 1所示,在小于7 Pa压力的真空状态下,试样被以20 ℃/s升温速率从室温加热到1 050 ℃,并在该温度保持300 s,然后以10 ℃/s的冷却速度冷却至变形温度,在变形前保温30 s,然后在不同变形温度进行60%变形量的等温变形,变形温度从600 ℃到1 000 ℃,温度间隔为40 ℃,应变速率为1 s-1。变形后,试样立即被淬灭到室温。通过热模拟机自动记录变形温度、应变和应力值。

|
图 1 热模拟压缩试验方案示意图 Figure 1 Schematic diagram of thermal simulation compression test |
图 2显示了钢种A1、BA、A2和A3在高温热模拟压缩试验得到的应力应变曲线。从单个应力应变曲线而言,曲线整体呈现出明显的稳态流变特征。在变形初期的弹性变形阶段,应力随应变的增加而急剧上升。发生塑性变形之后,位错增值引起的加工硬化和动态回复和动态再结晶带来的软化效应达到平衡,应力逐渐趋于平缓[3-4]。

|
图 2 试验钢种在不同变形温度下的应力应变曲线(a)A1、(b)BA、(c)A2和(d)A3 Figure 2 Stress-strain curves of studied steels at different deformation temperatures (a)A1、(b)BA、(c)A2 and(d)A3 |
对同一钢种不同变形温度下的曲线而言,图 2(b)、(c)、(d)中的应力随着变形温度的升高而降低,一方面主要因为变形温度升高造成原子热振动增强,原子间作用力减弱,变形阻力减小;另一方面更高温度下的变形,使相变或者再结晶的形核和晶粒长大更加容易,其带来的软化效应更明显。但在图 2(a)中,变形温度提高到840 ℃时,其应力却比800 ℃和760 ℃时更高,这主要因为840 ℃变形是在奥氏体区进行,而800 ℃变形却在两相区进行导致。
对每个钢种在不同变形温度下的变形抗力曲线,进行应变0到0.8的积分,得到该钢种在对应变形温度下的流变应力值。按照不同的C含量、Si含量及Mn含量分类,获得图 3所示的3个流变应力-变形温度曲线。从图 3(a)可以发现,对于低C的钢种A1而言,在800 ℃有变形抗力的明显降低。类似的现象也出现在了图 3(b)中B3钢种的流变应力-变形温度曲线和图 3(c)中C1钢种的流变应力-变形温度曲线上。

|
图 3 试验钢种的流变应力-变形温度曲线 Figure 3 Flow stress-deformation temperature curves of studied steels |
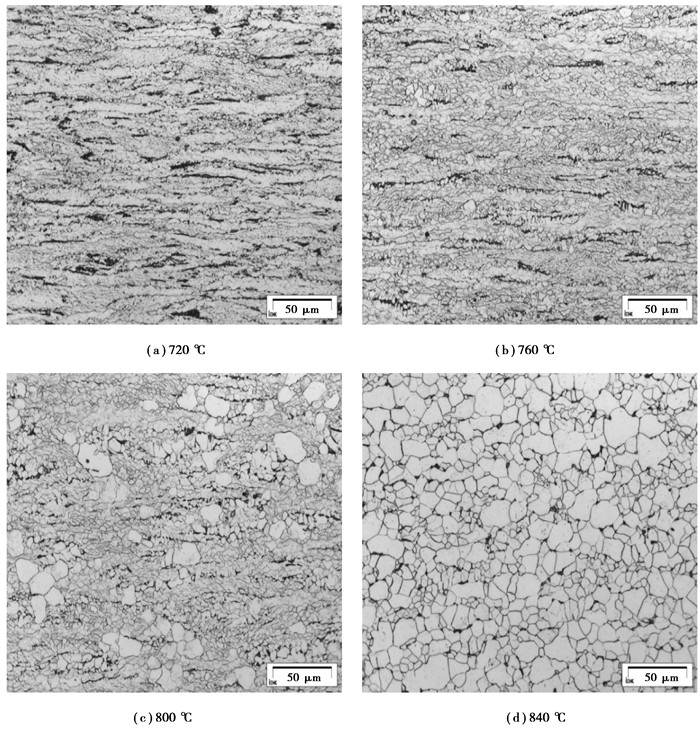
图 4为钢种A在不同变形温度下变形及淬火后的组织,对比这4张组织可以发现, 在840 ℃变形后,组织为等轴的铁素体晶粒,显示该试样在变形时为完全奥氏体状态,在变形后发生铁素体相变,因此,得到等轴的铁素体晶粒。从800 ℃变形温度开始,组织中呈现大小不一的混晶组织,并且部分呈纤维状分布,显示该温度下变形时,试样部分已经发生铁素体转变,即已经进入两相区。而760 ℃和720 ℃变形条件下,淬火后的组织进一步呈拉长状态,显示试样已经发生更多的铁素体转变。据此,对于试样A1而言,在试验冷却速度下,可以定义其铁素体相变开始温度Ar3为800 ℃。按此方法,可以获得所有试验钢种的Ar3温度。
|
图 4 钢种A1在不同温度下变形后的显微组织 Figure 4 Microstructures of steel A1 after deformation at different temperatures |
同时,在图 3(a)中,试样A1的流变应力在高于840 ℃的高温段,流变应力随着变形温度的降低而升高,然而在800 ℃的变形温度时,其流变应力却明显降低,小于840 ℃变形温度下的流变应力。该现象主要因为试样A1在800 ℃下发生铁素体相变,相同温度下铁素体组织的流变应力小于奥氏体。因此,流变应力-变形温度上这个转折,也说明了试样A1在该条件下的铁素体相变转变温度Ar3大约为800 ℃。然而,用这个方法确定Ar3只对部分钢种有效,因为对于另一部分钢种而言,在两相区流变应力的值并没有发生转折而降低,比如A2、C3等。
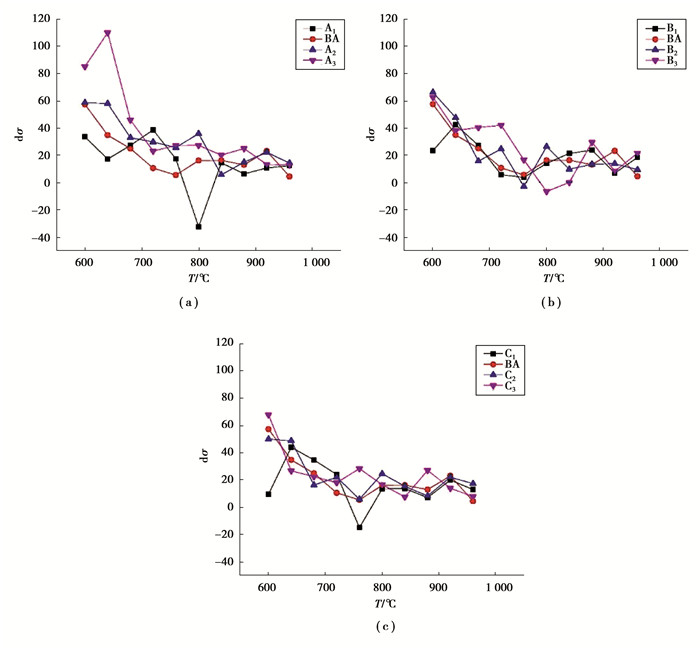
2.3 流变应力的降幅dσ的确定将某个变形温度下的流变应力值和比它高40 ℃变形温度下的流变应力值作差,即StressT-StressT+40定义这个差值为流变应力的降幅dσ。将这个变化量dσ作为纵坐标,将变形温度作为横坐标,可以得到如图 5所示的流变应力差值-变形温度曲线。在此曲线中,当流变应力的变化量为正值时,表明该温度下相对比它高40 ℃的温度,流变应力有所增加。当此变化量为负值时,则说明在此温度随着变形温度的降低,流变应力同步降低。
|
图 5 研究钢种在不同变形温度下流变应力差值-变形温度曲线 Figure 5 Flow stress difference-deformation temperature curves at different deformation temperatures for studied steels |
按照上述方法,记录所有10个试验钢种在两相区的流变应力降幅。如果在图 5中,对某个钢种只有一个流变应力变化值为负的情况,则取这个负值作为降幅。如果对某个钢种在连续多个温度下,流变应力的变化值若为负值,则将这个负值的和作为流变应力在两相区的降幅,比如钢种B3。
2.4 合金元素对Ar3和dσ的影响不同试验钢种的铁素体相变开始温度Ar3和流变应力的降幅dσ值汇总于表 2。利用MATLAB,将C,Si,Mn含量对Ar3的影响进行多元一次回归,其影响关系可以用式(1)表征。
| 表 2 试验钢种中C、Si、Mn含量、铁素体相变温度Ar3和流变应力降幅dσ Table 2 Ferrite transformation start temperature Ar3 and flow stress decrease dσ for studied steels |
| $ {\rm{A}}{{\rm{r}}_3} = 806-163{\rm{C}} + 58.3{\rm{Si}}-67.2{\rm{Mn}}。$ | (1) |
其中,模型的标准方差S为26.3279,R-Sq为83.9%,R-Sq(adj)为75.8%,显示了较好的相关性。式(1)显示主要合金元素中,C对铁素体相变开始温度Ar3的影响效果最明显,增加碳含量可以极大地降低Ar3的值。由于热模拟试验中没有改变试样变形前的冷却速度,同时在试样变形前进行了30 s的等温,因此,相对于其他研究者的结果,此处没有将冷却速率纳入考虑。
类似的方法对流变应力的降幅进行多元一次回归,获得式(2)所示模型。
| $ {\rm{d}}\sigma =-34.7 + 93.2{\rm{C}}-1.93{\rm{Si}} + 30.2{\rm{Mn}}{\rm{。}} $ | (2) |
其中,模型的标准方差S为10.3580,R-Sq为86.5%,R-Sq(adj)为79.8%,同样显示较好的相关性。
3 结论1) 流变应力-变形温度曲线显示,由于相同温度下奥氏体的变形抗力比铁素体大,研究钢种在低C含量、高Si含量以及低Mn含量的情况下,在钢种的两相区出现了流变应力随着变形温度降低而降低的现象。
2) 通过变形后的显微组织,结合流变应力-变形温度曲线上流变应力的拐点,可以确定试验条件下钢种的铁素体相变开始温度Ar3。
3) 建立了主要合金元素对铁素体相变开始温度Ar3的影响模型,同时两相区内流变应力的降幅也可以通过拟合的模型进行预测。
| [1] |
王健, 王宇, 谢红飙, 等.
基于热连轧实测数据的金属材料变形抗力模型[J]. 塑性工程学报, 2015, 22(1): 55–60.
WANG Jian, WANG Yu, XIE Hongbiao, et al. Deformation resistance model based on measured data of hot rolling[J]. Journal of Plasticity Engineering, 2015, 22(1): 55–60. (in Chinese) |
| [2] |
张有余.
高级别管线钢的组织性能及变形抗力模型[J]. 钢铁研究学报, 2013, 25(6): 40–43.
ZHANG Youyu. Deformation resistance modeling and microstructure and properties of high grade pipeline steel[J]. Journal of Iron and Steel Research, 2013, 25(6): 40–43. (in Chinese) |
| [3] |
王勇, 胡建旗, 徐永红, 等.
电刷材料Ag-Pd-Cu-X合金的热变行为分析[J]. 重庆大学学报, 2014, 37(3): 10–15.
WANG Yong, HU Jianqi, XU Yonghong, et al. Study on hot compression deformation behavior of a brush alloy Ag-Pd-Cu-X[J]. Journal of Chongqing University, 2014, 37(3): 10–15. DOI:10.11835/j.issn.1000-582X.2014.03.002 (in Chinese) |
| [4] |
彭晓东, 李俊辰, 易泓宇, 等.
AZ31-0.5Sr-1.5Y热变形行为分析[J]. 重庆大学学报, 2013, 36(9): 106–112.
PENG Xiaodong, LI Junchen, XU Yonghong, et al. Deformation behavior of alloy AZ31-0.5Sr-1.5Y at elevated temperature[J]. Journal of Chongqing University, 2013, 36(9): 106–112. DOI:10.11835/j.issn.1000-582X.2013.09.017 (in Chinese) |
| [5] | Gokyu I, Kihara J. On the temperature and strain-rate dependence of low carbon steels and an ultra low carbon 2% aluminum iron[J]. Tetsu-to-Hagane, 2010, 52(5): 837–853. |
| [6] | Sakai T, Ohashi M. Effect of temperature, strain rate, and carbon content on hot deformation of carbon steels[J]. Tetsu-to-Hagane, 2009, 67(11): 2000–2009. |
| [7] | Nagasaki C, Kihara J. Dependence of flow stress of steels at elevated temperature on the content of micro alloying elements[J]. Tetsu-to-Hagane, 2010, 81(8): 773–779. |
| [8] | Nagasaki C, Kihara J. Effect of cabon content on deformation resistance of cabon steels in austenite temperature range(hot rolling)[J]. Tetsu-to-Hagane, 2009, 74(7): 1418–1425. |
| [9] |
刘战英, 周满春, 王涛.
IF钢铁素体区轧制的变形抗力模型[J]. 塑性工程学报, 2005, 12(5): 92–95.
LIU Zhanying, ZHOU Manchun, WANG Tao, et al. Resistance matrix of IF steel rolled in ferrite region[J]. Journal of Plasticity Engineering, 2005, 12(5): 92–95. (in Chinese) |
| [10] |
孙本荣.
(γ+α)两相区控轧时变形抗力与显微组织的关系[J]. 钢铁, 1991, 26(9): 37–40.
SUN Benrong. Deformation resistance and microstructure in (γ+α) region during controlled rolling[J]. Iron and steel, 1991, 26(9): 37–40. (in Chinese) |
| [11] |
王涛.
IF钢两相区变形抗力规律[J]. 河北理工大学学报, 2008, 30(4): 23–26.
WANT Tao. The law of deformation resistance of IF steel in two-phase region[J]. Journal of Hebei polytechnic university, 2008, 30(4): 23–26. (in Chinese) |
| [12] |
李维刚, 陈水宣, 刘相华.
热轧带钢精轧过程考虑相变的轧制力模型[J]. 东北大学学报(自然科学版), 2013, 34(10): 1425–1429.
LI Weigang, CHEN Shuixuan, LIU Xianghua. Rolling force model considering phase transformation for hot strips during finishing process[J]. Journal of Northeastern University(Natural Science), 2013, 34(10): 1425–1429. DOI:10.3969/j.issn.1005-3026.2013.10.014 (in Chinese) |
| [13] |
李维刚, 冯宁, 王慎德, 等.
热轧相变过程变形抗力模型研究与开发[J]. 钢铁, 2017, 52(6): 61–66.
LI Weigang, FENG Ning, WANG Shende, et al. Research and development of deformation desistance model for phase transformation process of hot-rolled strips[J]. Iron and Steel, 2017, 52(6): 61–66. (in Chinese) |
| [14] | Mintz B, Banerjee J R, Banks K M. Regression equation for temperature for coarse grained as cast steels[J]. Ironmaking & Steelmaking, 2011, 38(3): 197–203. |
| [15] | Ouchi C, Sampei T, Kozasu I. The effect of hot rolling condition and chemical composition on the onset temperature of γ-α transformation after hot rolling[J]. ISIJ International, 2006, 22(3): 214–222. |
 2018, Vol. 41
2018, Vol. 41

