1b. 辽宁工程技术大学 煤炭资源安全开采与洁净利用工程研究中心, 辽宁阜新 123000;
2. 内蒙古霍林河露天煤业股份有限公司南露天煤矿, 内蒙古 霍林郭勒 029200
1b. Research Center of Coal Resources Safe Mining and Clean Utilization, Liaoning Technical University, Fuxin 123000, Liaoning, P. R. China;
2. South Open-pit Coal Mine, Inner Mongolia Huolinhe Open-pit Coal Industry Co., Ltd., Huolingle 029200, Inner Mongolia, P. R. China
排土场建设是露天矿山工程的重要环节之一,由于其自身费用占据矿山工程成本费用比重较大,长期以来一直作为矿山设计的重点研究方向。对于露天煤矿排土场规划问题通常包括排土场位置选择、排土参数确定以及排土场发展规划等三方面内容[1],其总体目标是确定一个技术上可行且总体经济利益最大化的排土计划编制,此类问题其本质上是一类大规模土岩搬运的系统工程。对于露天煤矿待排弃物料量通常是开采矿物量的几倍甚至十几倍,其运输费用占露天矿山总体成本费用的40%~50%。因此,在完成排土场设计的基础上深层次挖掘排土工程时空关系,优化土岩流向流量规划模型对进一步控制运输功、降低运输成本具有现实的经济意义。
目前,国内外针对排土规划的相关问题研究,所采用的方法主要集中于基于边坡稳定性分析计算的排土参数优化、考虑节地及土壤恢复的排土工程设计和以经验编制为主的排土方案费用比选等[2-7],其中不乏基于安全、土地复垦、节地等考虑的新方法、新论断,对于排土场优化设计、改善排土场结构均起到了积极的作用,部分成果在工程管理及成本费用控制等方面具有较为突出的优化效果,但其采用的方法多围绕排土场建设、排土参数优化以及排土程序方案设计展开,优化结果中均缺乏对于排土场内部土岩流向及流量的规划编制,缺乏对于物料堆置位置的最优化考虑。但随着露天矿山开采深度逐步加深,排土运输工程费用过高等不合理问题变得越发尖锐,传统的人工经验设计很难达到待优化的目标。因此,有计划的进行排土场内部土岩结构及流向流量等相关优化,对进一步降低排土运输成本具有显著的现实意义。近年来,也不断有学者提出在对已完成设计的排土场进行堆置次序优化,对于控制排土费用成本的重要意义。如刘佶林等[8-9]提出基于最优堆置体的搜索算法,用以解决土岩派往排土场哪个位置堆置最优的问题;Li等[10-13]提出采用混合整数规划求解排土堆置次序优化模型的方法。
在上述研究成果基础之上,笔者总结了传统排土规划方法在多排土场间规划存在的缺陷,并针对于现阶段尚未解决的多排土间物料规划问题,提出一种面向多排土场间自身堆排发展建设的最优化模型,并基于动态规划嵌套0-1整数规划决策的方法设计了一种求解优化模型的高效算法。结合神华新疆黑山露天矿外排期间多排土场间排土物料规划不合理、运输成本高等现实工程问题,应用文中算法进一步优化该矿排土运输费用成本,并获得较为理想的优化效果。
1 土岩物料堆置规划建模为优化排土场结构,进一步控制矿山排土运输成本,以分治思想为算法基础,从排土场自身发展建设及多排土间时空关系约束入手,分阶段构建排土场规划模型。
1.1 术语定义1) 发展方式概化模型:该术语由文献[14]定义,具体划分方法可参见文献[14],其本质是一类根据排土设计而人为按照排土场发展方式进行规则序列化的概念模型。
2) 概化模型阶段:在概化模型基础上,按照指定条带数划分形成,且存在一定工程联系的作业区域;
3) 规划模型阶段:为适应动态规划算法达到分割问题规模的目的,通过人为引进时空约束的方法建立的规划算法决策范围。
4) 块体模型:为进一步刻划地质统计学属性信息而构建的离散化规则体元模型,表现形式为具有次级块体的规则立方体模型。
1.2 参数指标体系的建立T={t|t=1, 2, 3, …, n}表示排土场集合;Bt={b|b=1, 2, 3, …,n}表示排土场内块体模型集合;w表示阶段内的总运输功函数,t表示排土场序号;i表示排土阶段序号;j表示阶段内排土带序号;k表示排土条带内的第k个块体;变量Mt, j, ki表示对应位置块体物料量;变量dt, j, ki表示自排土场入口至对应位置块体的运距;变量St, j, ki表示对应位置块体是否被堆置;Rc状态变量,记录当前概化模型阶段以及块体序号;JtRc当前排土位置所处阶段的排土条带总和。
1.3 决策变量定义| $ S_{t, j, k}^i = \left\{ \begin{array}{l} 1\;\;\;\;\;B_{t, j, k}^i 是否被占用, \\ 0\;\;\;\;\;\;\;\;\;\;\;\; 其他, \end{array} \right. $ | (1) |
式中:i表示排土阶段序号;j表示阶段内排土带序号;k表示排土条带内的第k个块体。
1.4 目标函数整个堆置次序优化问题建立在排土场内部总体运输功最小的目标之下,需计算每个移运块体的运输功,并由计算结果决定块体被优化堆置的实际位置。通常,对于该类问题进行整体求解常无法得到有效解。为此,文中在发展方式概化模型基础上,提出一种阶段内动态决策方法,用以实现总体问题的分阶段动态决策。其方法是在排土场内部的每一个排土决策阶段均建立一个运输功计算模型,如式(2)所示。
| $ W = \sum\nolimits_{t = 1}^T {\sum\nolimits_{j = 1}^{J_t^i} {\sum\nolimits_{k = 1}^{{K_j}} {\left( {M_{t, j, k}^i \cdot d_{t, j, k}^i} \right)} } }, $ | (2) |
式中:i=1, 2, 3…,I; dt, j, ki变量的距离计算起点为当前排土场的排土干线入口。
其中规划的阶段是依靠上一阶段决策结果动态划分产生的,各阶段的决策会产生下一个阶段的新状态,其决策过程即为求解式(2)中的最小化问题,按照0-1整数规划建立最优化模型如式(3)所示。
| $ J = \min \left\{ {\sum\nolimits_{t = 1}^T {\sum\nolimits_{j = 1}^{J_t^i} {\sum\nolimits_{k = 1}^{{K_j}} {\left( {M_{t, j, k}^i \cdot d_{t, j, k}^i \cdot S_{t, j, k}^i} \right)} } } } \right\}, $ | (3) |
式中符号含义同上。
1.5 约束条件充分考虑到排土工程在时空关系以及工程量等方面的约束,对0-1整数规划模型建立如下几方面的约束:
阶段性工程量约束
| $ \begin{array}{l} \sum\nolimits_{t = 1}^T {\sum\nolimits_{i={R_{\rm{c}}}}^{i = R{'_{\rm{c}}}} {\sum\nolimits_{j = 1}^{J_t^i} {\sum\nolimits_{k = 1}^{{K_j}-1} {\left( {M_{t, j, k}^i \cdot S_{t, j, k}^i} \right)} } } } < M_{\rm{S}}^i \le \\ \sum\nolimits_{t = 1}^T {\sum\nolimits_{i={R_{\rm{c}}}}^{i = R{'_{\rm{c}}}} {\sum\nolimits_{j = 1}^{J_t^i} {\sum\nolimits_{k = 1}^{{K_j}} {\left( {M_{t, j, k}^i \cdot S_{t, j, k}^i} \right)} } } } ; \end{array} $ | (4) |
条带间发展次序约束
| $ S_{t, j, k}^i \ge S_{t, j + 1, x}^i; $ | (5) |
阶段间发展约束
| $ \left\{ \begin{array}{l} ①\sum\nolimits_{j = 1}^{J_t^{{R_{\rm{c}}}}} {\sum\nolimits_{k = 1}^{{K_j}} {\left( {S_{t, j, k}^{{R_{\rm{c}}}}} \right)} } = \sum\nolimits_{j = 1}^{J_t^{{R_{\rm{c}}}}} {\sum\nolimits_{k = 1}^{{K_j}} 1 } \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;R{'_{\rm{c}}}-{R_{\rm{c}}} = 1, \\ ②\sum\nolimits_{i = {R_{\rm{c}}}}^{R{'_{\rm{c}}}-1} {\sum\nolimits_{j = 1}^{J_t^i} {\sum\nolimits_{k = 1}^{{K_j}} {\left( {S_{t, j, k}^i} \right)} } } = \sum\nolimits_{i = {R_{\rm{c}}}}^{R{'_{\rm{c}}}-1} {\sum\nolimits_{j = 1}^{J_t^i} {\sum\nolimits_{k = 1}^{{K_j}} 1 } } \;\;\;{\rm{if}}\;R{'_{\rm{c}}} - {R_{\rm{c}}} > 1; \end{array} \right. $ | (6) |
决策变量与排土场块体数量关系
| $ \sum\nolimits_{t = 1}^T {\sum\nolimits_{i = {R_{\rm{c}}}}^{i = R{'_{\rm{c}}}} {\sum\nolimits_{j = 1}^{J_t^i} {\sum\nolimits_{k = 1}^{{K_j}} {\left( {S_{t, j.k}^i} \right)} } } } = \sum\nolimits_{t = 1}^T {K_t^i} 。$ | (7) |
动态规划算法[15-20]是一类解决多阶段决策的优化方法,同时也是一种在分阶段可选策略中逼近预期目标的最优化手段。因此,算法本身要求求解模型具有时间或空间上的阶段划分,以便对原问题进行分治求解。根据预先设计好的发展方式概化模型及排土运输线路,进行动态的决策阶段划分,具体划分方法需从如下几方面考虑:
1) 概化模型[14]阶段划分。在设计位置基础上,按照排土场发展方式设计,以该矿排土带宽度为基础划分单元,按照发展方式构建排土条带的工程发展次序模型。
2) 阶段内块体属性赋值。由优化模型式(3)可知,整个规划问题的综合评价指标即为阶段内的运输功,为进一步构造优化模型中目标函数,需对每个块体赋予物料量及运距等计算参数。其计算方法需首先对规则块体模型尺寸参数进行反向计算,获得块体容纳物料量;并对运距实施的推估,具体方法需要依据现阶段所处位置及排土运输系统设计,并利用前一阶段的路径状态迭代推估下一个条带内各块体的运距属性,最终将上述属性单独赋值给各块体模型。
3) 决策阶段动态划分。动态阶段划分的目标是为使动态规划算法获得依赖工程实际的子问题划分,具体的划分原理如图 1所示,其中式(8)表示各阶段工程量计算表达式,图 1中A、B分别表征南部和北部卡车排土场,A1中序号表征南部卡车排土场概化模型第一阶段,MA1、MB1分别示意A、B排土场概化模型第一阶段的物料量,其形成的阶段间物料总量计算方法如式(8)示。在划分过程中,将概化模型中的不同排土阶段作为划分模型的变量初始状态,首先将A、B两排土场总量作为决策阶段的物料总量,进行位置决策。若假设MA1和MB1的量全部派往A排土场最优,则依赖决策结果动态生成第二决策阶段。执行上述操作即可获得阶段的动态划分。在上述物料决策阶段会存在两类不同的计算策略:
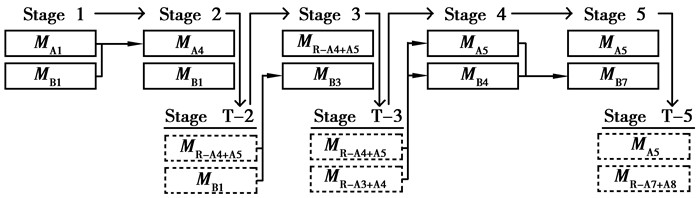
|
图 1 阶段划分原理图 Figure 1 Phase division schematic diagram |
策略1:如Stage 1至Stage T-2在第二阶段规划中MA4并非完整的条带,规划过程会采用式(8)②式策略在A排土场规划量基础上追加A5,以保证所有规划过程初始化时均为完整条带;
策略2:如Stage T-3至Stage 4,Stage T-3的物料在Stage 4排弃时可直接获得完整的初始化条带,因此直接采用式(8)①式进行计算,规定Stage 1的前向阶段量
| $ M_{\rm{s}}^i = \left\{ \begin{array}{l} ①\sum\nolimits_{t = 1}^T {\left[{\sum\nolimits_{j = 1}^{J_t^{{R_{\rm{c}}}}} {\sum\nolimits_{k = 1}^{{K_j}} {\left( {{M_{t, j, k}}} \right)} }-\sum\nolimits_{j = 1}^{{{\left( {J_t^{{R_{\rm{c}}}}} \right)}^*}} {\sum\nolimits_{k = 1}^{{{\left( {K_{_j}^{{R_{\rm{c}}}}} \right)}^*}} {\left( {{M_{t, j, k}}} \right)} } } \right]}, \\ ②\sum\nolimits_{t = 1}^T {\left[{\sum\nolimits_{j = 1}^{J_t^{{R_{\rm{c}}}} + 1} {\sum\nolimits_{k = 1}^{{K_j}} {\left( {{M_{t, j, k}}} \right)} }-\sum\nolimits_{j = 1}^{{{\left( {J_t^{{R_{\rm{c}}}}} \right)}^*}} {\sum\nolimits_{k = 1}^{{{\left( {K_{_j}^{{R_{\rm{c}}}}} \right)}^*}} {\left( {{M_{t, j, k}}} \right)} } } \right]}, \end{array} \right. $ | (8) |
式中:Msi表示i阶段的物料总量;Rc状态变量,记录当前概化模型阶段以及块体序号;JtRc当前排土位置所处阶段的排土条带总和;Mt, j, kRc当前排土区段上的块体物料量;(JtRc)*完成规划的排土条带总数;(KjRc)*完成规划的排土块体总数。
2.2 优化决策过程对于黑山露天矿整个次序规划问题的核心部分即为优化决策阶段,决策过程是产生当前阶段的最优化堆排位置的前提,同时也是阶段划分的状态基础。决策过程实质是对阶段内物料量进行运输功最小化的0-1整数规划过程,具体步骤如图 2所示,算法的核心步骤如下:
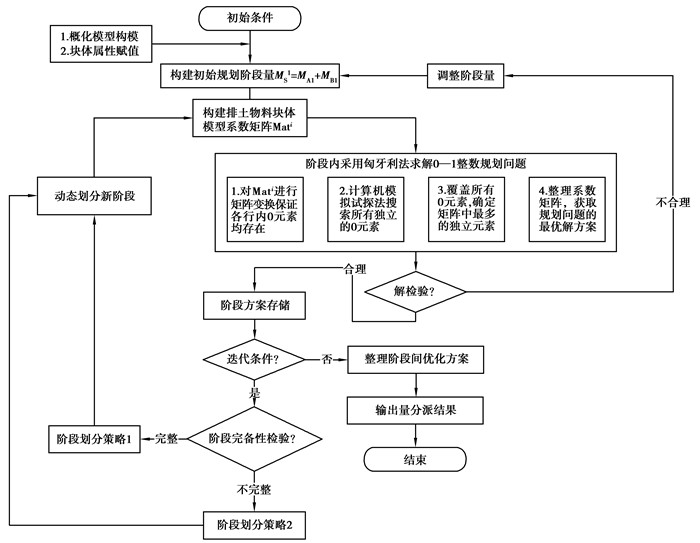
|
图 2 阶段内次序规划算法决策过程 Figure 2 The decision-making process of sequence planning algorithm in phase |
1) 在已建立的黑山露天矿发展方式概化模型的基础上,根据式(8)中式①计算第一阶段堆置物料总量Ms1,并构建第一个动态规划阶段;
2) 自概化模型第一阶段开始,枚举各排土场单独完整收容Ms1时所占用的排土区段,并提取区段内部块体标记为集合Bi,进一步将决策问题求解范围缩小至Bi中,以控制决策变量规模;
3) 枚举集合Bi中块体的物料量及运距,构建系数矩阵,将矩阵映射的属性参数带入式(3)的0-1整数规划模型,规划出在式(4)~(7)约束下物料Ms1在集合Bi中的最优堆排位置;
4) 提取各排土场当前所处区段记为Rc,排土条带记为JtRc,条带内块体序号记为KJtRc,并组织上述信息进行完备性检验,并构建新的排土阶段,其初始状态记为S2;
5) 提取第一阶段决策变量St, j, ki为1的块体,标记为第一阶段堆置优化序列P1存储;
6) 以第二排土阶段状态量S2中各排土所处区段位置为界限约束,动态划分第二排土阶段,并计算第二阶段堆置物料总量时,如果KJtRc >0则采用式(8)中②式计算方法,在阶段剩余条带基础上追加完整条带,如图 1中Stage T-2所示,否则如图 1中Stage 4所示;
7) 判断迭代条件,成立则迭代执行(2)~(5),阶段性输出Pi,i>1,否则结束。
3 实例分析 3.1 工程背景神华新疆托克逊黑山露天煤矿设计生产能力10.0 Mt/a,服务年限104 a,地表走向平均长15.84 km,地表倾向平均宽2.70 km,开采深度50~318 m,最终帮坡角北帮20°。黑山露天煤矿煤层埋藏较深、倾角大,初期纵向开采无法实现内排,同时该矿地貌主要为高山、沟谷地形,受山区地形条件的限制,外排土场分散布置
多处。煤层倾斜赋存、高山、沟谷发育的地形地貌,导致露天开采的剥离物运距大、提升高度大。2015年平均运距达到3.8 km,最大单程运距超过5 km;2015年平均提升高程达到100 m,最大提升运距超过180 m;随着矿山工程的发展,运距和提升高度将不断增大,生产效益会进一步恶化。
黑山露天煤矿初始拉沟位置在首采区东北部,上部表土剥离采用单斗-卡车开采工艺,由于首采区不具备内排条件,首采区物料全部外排,设计规划两个外排土场包括北部卡车排土场和南部卡车排土场,其中北部卡车排土场占地1.77 km2,南部卡车排土场占地9.09 km2。规划北部排土场具有一条运输干线,现阶段干线入口距采场出口0.56 km;规划南部卡车排土场具备两条排土干线,现阶段东部干线入口距采场出口1.82 km,西部干线入口距采场出口1.68 km,具体排土场设计参数如表 1所示。
| 表 1 卡车外排土场参数 Table 1 Parameters of track dump |
根据排土设计规划该矿2025年初始内排,2028年实现完全内排,故期间剥离物料量均由南、北卡车排土场收容,其中各年的物料排弃量如表 2所示。由于南部卡车排土场规划距离首采区较远,北排排弃空间耗尽至完全内排期间,将面临运距不断增大,生产效益不断恶化。因此,对于该矿外排期间进行合理的物料流流向流量规划对于该矿具有现实的经济意义。
| 表 2 外排土场计划分配物料量 Table 2 The planned distribution of materials in truck dump |
为论证文中算法的现实有效性,文中采用动态规划方法对黑山露天矿南部卡车排土场及北部卡车排土场建模,并优化原有2017—2027年间外排规划设计,该方法能保证在阶段内目标最优条件下,动态的调整多排土场间多阶段内的物料调配,较之原始设计中以最短距离为依据的经验主义设计、缺乏多排土场间协调调运配合的方法,具有极为明显的能耗优化效果,整个优化算法的决策阶段划分及阶段间物料量分配情况如表 3所示。
| 表 3 阶段间规划量 Table 3 The planning material quantity between stages |
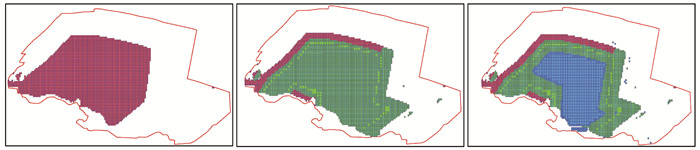
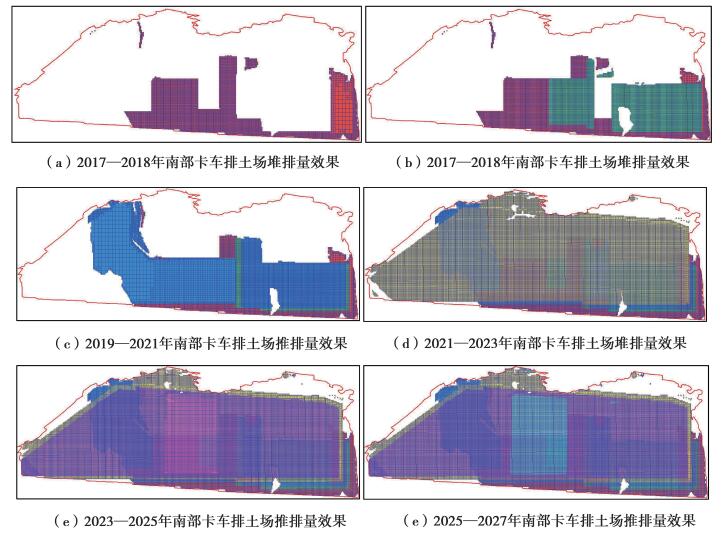
根据表 3规划结果,文中采用3DMine矿业软件对规划进行可视化建模,其中图 3和图 4分别为2017—2027年间南、北外排土场最优规划位置。
|
图 3 北部卡车排土场块体模型堆排结果 Figure 3 The results of the pile row of the north truck dump |
|
图 4 南部卡车排土场块体模型堆排结果 Figure 4 The results of the pile row of the south truck dump |
文中将整个次序优化问题抽象为一个基于运输功能耗最小化为目标的决策问题,其核心目标是达到规划问题的全局能耗最优解。因此,根据表 3中的规划结果,文中建立图 5的运输功耗费对比图用以衡量优化效果。从能耗对比图中不难看出,黑山露天矿原有设计随着北部排土场逐步接近最终收容状态,受南部排土场运距较大限制,总体运输功大幅增长。文中算法在原有设计待排量基础上,通过细化两排土场间堆置位置决策、求解各决策阶段内的排土最优化位置,有效的压缩了整体运输功,获得最终运输功能耗最小时的堆排位置,较大幅度的优化了原始设计的运输能耗。
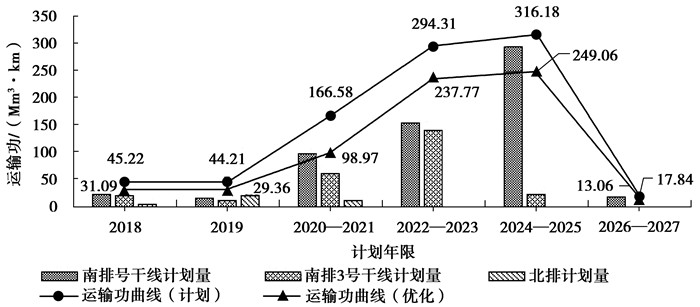
|
图 5 运输功能耗对比图 Figure 5 Transport functional comparison chart |
对于优化效果的最直接表现即为费用成本对比,为进一步表现文中算法对于原设计的优化效果,文中根据黑山露天煤矿的历史实践中卡车的单位体积剥离物料运输成本统计,并对图 5中对比结果进行了费用换算,并绘制费用对比曲线图 6。其中对成本指标取值为:剥离卡车运输距离小于3 km时,单位体积运输成本取5.34元;考虑运距过大对整个运输系统综合的影响,当超出3 km运距范围时每公里追加运输成本1.27元;卡车单位提升成本取0.019元/m。
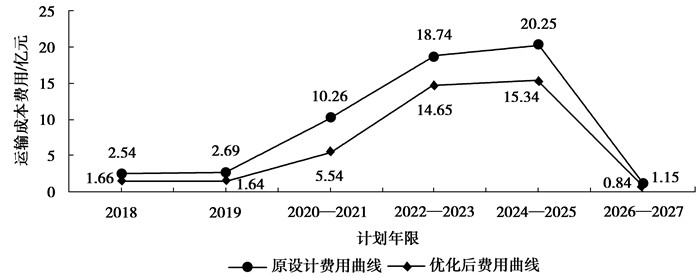
|
图 6 运输费用变化曲线 Figure 6 Transport cost curve |
通过对比图 6中费用变化曲线可发现,优化算法量化了传统基于经验的决策过程,较大幅度的优化了排土场自建设过程中的费用成本,针对黑山露天矿受南排运距影响的费用成本过高等现实问题,文中引进的排土场内部结构优化算法可为矿山每年节省1~2亿元的运输费用成本,对于改进排土结构优化具有较为明显的现实意义。
4 结论1) 针对于传统排土设计缺乏内部堆置规划的现实问题,建立以最小运输功为优化目标的次序规划模型,并提出一种阶段间嵌套0-1整数规划辅助决策的动态求解算法,有效解决了设计中物料流分配不合理的问题。
2) 优化算法基于多排土间规划问题建立,同时适用于单排土场问题求解,对于排土规划问题求解具有普适性。
3) 由于受地形等条件限制黑山露天矿南部卡车排土场规划位置较远,原设计运输成本较高,通过优化南、北卡车排土场内部堆置次序,有效压缩了该矿2017—2027年首采区外排期间的物料运输功能耗,进一步控制了运输成本。
4) 通过运输费用对比发现,与原设计运输费用投入相比,2018年节省0.88亿元、2019年节省1.05亿元、2020—2021年节省4.72亿元、2022—2023年节省4.09亿元、2024—2025年节省4.91亿元、2025—2027年节省0.31亿元。
| [1] |
北京矿业学院露天采矿教研组, 阜新煤矿学院露天采矿教研组. 露天采矿学[M]. 北京: 中国工业出版, 1981: 154-166.
Beijing Institute of Mining Open-pit Mining Research Group, Fuxin Institute of Coal Mining Open-pit Mining Research Group. Open-pit mining[M]. Beijing: China Industry Press, 1981: 154-166. (in Chinese) |
| [2] |
石建勋, 刘新荣, 廖绍波.
矿区排土场堆载对边坡稳定性影响的分析[J]. 采矿与安全工程学报, 2011, 28(2): 258–262.
SHI Jianxun, LIU Xinrong, LIAO Shaobo. Analysis of slope stability affected by load of waste dump of mining area[J]. Journal of Mining & Safety Engineering, 2011, 28(2): 258–262. (in Chinese) |
| [3] |
孙永凡, 张瑞新.
露天矿排土场段高及境界的优化[J]. 中国矿业大学学报, 1992, 21(4): 41–47.
SUN Yongfan, ZHANG Ruixin. The optimization of the boundary and bench height of the surface mine dumps[J]. Journal of China University of Mining & Technology, 1992, 21(4): 41–47. (in Chinese) |
| [4] |
蔡利平, 李钢, 史文中.
增地节地型露天矿排土场优化设计[J]. 煤炭学报, 2013, 38(12): 2208–2214.
CAI Liping, LI Gang, SHI Wenzhong. Optimal design for land l expanding and conserving open-pit dump[J]. Journal of China Coal Society, 2013, 38(12): 2208–2214. (in Chinese) |
| [5] |
李三川, 白润才, 刘光伟, 等.
露天煤矿排土场建设发展程序优化研究[J]. 煤炭科学技术, 2017, 45(3): 49–55.
LI Sanchuan, BAI Runcai, LIU Guangwei. Optimized study on construction and development program of dumping site in surface mine[J]. Coal Science and Technology, 2017, 45(3): 49–55. (in Chinese) |
| [6] |
郭成, 马萃林.
露天矿排土场堆置要素的优化[J]. 金属矿山, 2011, 40(1): 42–44, 63.
GUI Cheng, MA Cuilin. Optimization of heap parameters of open-pit waste dump[J]. Metal Mine, 2011, 40(1): 42–44, 63. (in Chinese) |
| [7] |
卫博, 付梅臣, 白中科.
基于节地的露天矿排土场设计[J]. 农业工程学报, 2006, 22(6): 230–232.
WEI Bo, FU Meichen, BAI Zhongke. Dump design for open cast mine based on land-conserving[J]. Transaction of the CASE, 2006, 22(6): 230–232. (in Chinese) |
| [8] |
刘佶林, 戴晓江, 王孝东.
露天矿排土运输优化的最优排土堆置体搜索算法研究[J]. 矿业研究与开发, 2016, 36(12): 13–18.
LIU Jilin, DAI Xiaojiang, WANG Xiaodong. The optimized dumping region searching algorithm of dumping transportation for open-pit mine[J]. Ming R&D, 2016, 36(12): 13–18. (in Chinese) |
| [9] |
刘佶林. 基于数字矿床模型的露天排运规划优化研究[D]. 昆明: 昆明理工大学, 2015. LIU Jielin. Optimization research of outdoor row transportation planning based on digital deposit model[D]. Kuming: Kunming University of Science and Technology, 2015. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10674-1016036841.htm |
| [10] | Li Y, Topala E, Williams D. Waste rock dumping optimisation using mixed integer programming (MIP)[J]. International Journal of Mining, Reclamation and Environment, 2013, 27(6): 425–436. DOI:10.1080/17480930.2013.794513 |
| [11] | Li Y, Topal E, Williams D J. Optimisation of waste rock placement using mixed integer programming[J]. Mining Technology, 2014, 123(4): 220–229. DOI:10.1179/1743286314Y.0000000070 |
| [12] | Li Y, Topal E, Ramazan S. Optimising the long-term mine waste management and truck schedule in a large-scale open pit mine[J]. Mining Technology, 2016, 125(1): 35–46. DOI:10.1080/14749009.2015.1107343 |
| [13] | Li Y. Optimum waste dump planning using mixed integer programming (MIP)[D]. Perth: Curtin University, 2014. |
| [14] |
罗阳华, 简文彬, 李宏达.
基于堆置效应的排土场稳定性分析[J]. 有色金属(矿山部分), 2016, 68(1): 89–93.
LUO Yanghua, JIAN Wenbin, LI Hongda. Stability analysis of the waste dump based on stacking effect[J]. Nonferrous Metals Engineering, 2016, 68(1): 89–93. (in Chinese) |
| [15] | Bolender M, Doman D. A non-linear model for the longitudinal dynamics of a hypersonic air-breathing vehicle[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston, Virigina: American Institute of Aeronautics and Astronautics, 2005: 2005-6255. |
| [16] | Song R, Xiao W, Zhang H, et al. Adaptive dynamic programming for a class of complex-valued nonlinear systems[J]. IEEE Transactions on Neural Networks & Learning Systems, 2014, 25(9): 1733–1739. |
| [17] | Fu J, He H, Zhou X. Adaptive learning and control for MIMO system based on adaptive dynamic programming[J]. IEEE Transactions on Neural Networks, 2011, 22(7): 1133–48. DOI:10.1109/TNN.2011.2147797 |
| [18] | Liu W, Venayagamoorthy G K, Wunsch D C. A heuristic-dynamic-programming-based power system stabilizer for a turbogenerator in a single-machine power system[J]. IEEE Transactions on Industry Applications, 2005, 41(5): 1377–1385. DOI:10.1109/TIA.2005.853386 |
| [19] | Wang D, Liu D, Li H, et al. Neural-network-based robust optimal control design for a class of uncertain nonlinear systems via adaptive dynamic programming[J]. Information Sciences, 2014, 282: 167–179. DOI:10.1016/j.ins.2014.05.050 |
| [20] | Wang D, Liu D, Li H. Policy iteration algorithm for online design of robust control for a class of continuous-time nonlinear systems[J]. IEEE Transactions on Automationence & Engineering, 2014, 11(2): 627–632. |
 2018, Vol. 41
2018, Vol. 41


