2. 中铁第一勘察设计院集团有限公司, 西安 710043;
3. 甘肃铁道综合工程勘察院有限公司, 兰州 730000;
4. 国家测绘地理信息局第一大地测量队, 西安 710054;
5. 东华理工大学 测绘工程学院, 南昌 330013
2. China Railway First Survey and Design Institute Group Co., Ltd., Xi'an 710043, P. R. China;
3. The General Engineering Survey Institute of Railways of Gansu Co., Ltd., Lanzhou 730000, P. R. China;
4. First Survey Team of State Bureau of Surveying and Mapping Geographic Information, Xi'an 710054, P. R. China;
5. School of Surveying and Mapping Engineering, Donghua University of Science and Technology, Nanchang 330013, P. R. China
目前,中国各省市之间正在加快开展高铁建设工作,由于高铁线路呈条带形状,高斯投影[1-3]容易导致长度变形并且容易超限,为防止投影长度变形超限,以往的做法主要是三种[4-6]:第一,抬高或抬低投影面,从而使投影高程归化改正值减小;第二,调整中央子午线,从而使投影长度变形减小;第三,投影面和中央子午线同时进行改变,从而使投影长度变形值满足限差允许值[7-11]。但是,方法一所述,通过抬高或降低投影面使其与椭球面尽量接近,无法很好地解决高斯投影对长度变形的影响,位于投影带边缘的横坐标数量值较大,必然导致投影变形过大[12-15]。方法二所述,调整中央子午线,对高程归化改正方面作用较小。方法三所述,在某些测区能起到很好的效果,特别是测区为块状的地形。然而,较长线路工程,测区长度可达上千公里,对于东西向跨度较大、远离中央子午线,以及地形起伏变化较大的条带测区,如果按照上述三种方法来解决高斯投影长度变形的问题显然很难满足国家规范的要求。鉴于此,文献[16-17]中采用法截面子午线来建立斜轴椭球的方法,目的是通过建立法截面子午线椭球来减小测区与斜轴椭球中央子午线的距离。然而,此方法的不便之处在于要选择合适的基准点和线路方位角来对斜轴椭球进行定位和定向,会使得计算过程及相关参数计算略显繁琐,也不便于相关软件的编制。因此,为减少投影分带以及投影变形,引入一种新的建立工程独立坐标系统对应椭球的方法[18],并通过高铁GPS控制网的具体实例对建立的工程椭球进行了验证和分析,试验结果表明文中所建立的工程椭球特别适合东西跨度较大的长线路工程,且长度综合投影变形值符合规范要求,对线路工程测量具有借鉴作用。
1 长度综合投影变形分析东西走向的带状测区,在进行高斯投影时会出现变形,对于东西跨度较大的测区,甚至无法满足工程建设需求。
在高斯投影中,长度变形主要由测区表面归算至参考椭球面的高程归化长度变形和参考椭球面投影至高斯平面产生的投影长度变形两部分组成,通常把高斯平面上的长度与实际测区地面的长度之差,称为长度综合变形,用计算式表达为
| $ \frac{{\Delta S}}{S} = \frac{{-{H_{\rm{m}}}}}{{{R_{\rm{A}}}}} + \frac{1}{2}{\left( {\frac{{{y_{\rm{m}}}}}{{{R_{\rm{m}}}}}} \right)^2}, $ | (1) |
式中:Hm为测区边相对于参考椭球面的高程,ym为测区边两点横坐标的平均值,S为投影边长,RA为测区边方向的参考椭球面法截弧的平均曲率半径。
在计算中,取Rm=RA=6 371 km,则式(1)可以写成
| $ \frac{{\Delta S}}{S} =-\frac{{{H_{\rm{m}}}}}{{{R_{\rm{A}}}}} + \frac{1}{2}{\left( {\frac{{{y_{\rm{m}}}}}{{{R_{\rm{m}}}}}} \right)^2} =-1.57 \times {10^{-4}}{H_{\rm{m}}} + 1.23 \times {10^{ - 8}}{y_{\rm{m}}}^2。$ | (2) |
由式(2)知:长度综合变形与测区的平均高程和测区的投影带位置有关,把长度综合变形的允许值±2.5 cm/km代入(2)式得
| $ \pm 2.5 =-1.57 \times {10^{-4}}{H_{\rm{m}}} + 1.23 \times {10^{-8}}{y_{\rm{m}}}^2。$ | (3) |
为顾及单位的统一和计算的方便,式(3)可以写成
| $ \pm 2.5 \times {10^{-5}} =-0.157 \times {10^{-5}}{H_{\rm{m}}} + 0.001{\rm{ }}23 \times {10^{ - 5}}{y_{\rm{m}}}^2, $ | (4) |
式(4)中,令H=Hm,ym=y,建立y与H之间的函数关系式,由式(4)可以整理得
| $ H = 0.783{y^2}({10^{-4}}) \pm 0.159。$ | (5) |
以H为纵坐标轴,y为横坐标轴,绘制式(5)的函数图像,如图 1所示。
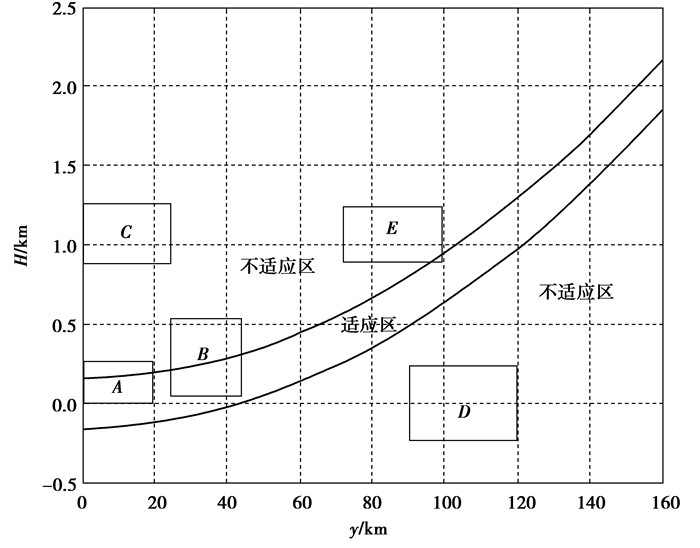
|
图 1 投影面高程与横坐标投影变形 Figure 1 Projection plane height and horizontal coordinate projection deformation |
图 1所示,A、B区表示在该区域范围内可以采用国家统一的坐标系,不适应区表示需要建立独立坐标系才能满足工程建设的需要。C区表示该区域主要为高海拔地区,长度变形主要是高程归化的影响。D区域距离中央子午线较远,长度变形主要是高斯投影带来的影响。而E区域会同时受到高程归化和高斯投影对边长变形的综合影响。
2 工程椭球的构建工程椭球建立的基本思想是:建立一个新椭球,该椭球是以地球参考椭球E0(也叫“基础椭球”)为基础,通过对基础椭球进行旋转、变形,让其中央子午线沿测区线路的延伸方向[19, 20]。在建立工程椭球时,为便于区分不同椭球,通常记E0为基础椭球,E1为旋转椭球,E2为工程椭球,具体建立步骤如图 2所示[18]。
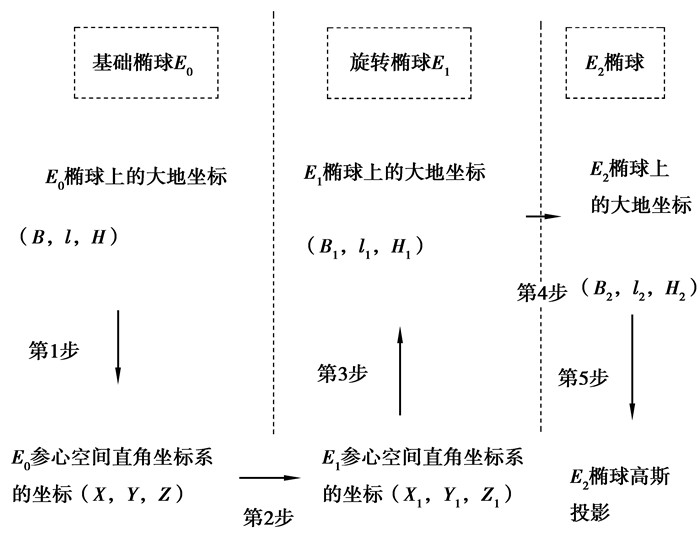
|
图 2 E2椭球构建步骤 Figure 2 E2 ellipsoid construction step |
如图 3所示,E0→E1参心空间直角坐标系的建立方法为[21]:在E0椭球中,分别以0°子午面与赤道交点C和赤道交点E建立X轴和Y轴,以指向北极的K方向建立Z轴,建立参心空间直角坐标系O-XYZ。
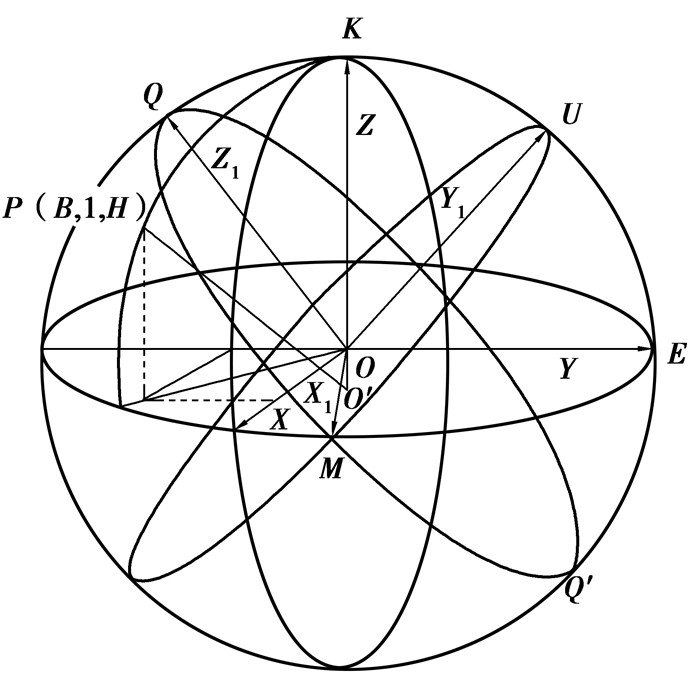
|
图 3 E0→E1参心空间直角坐标系的建立 Figure 3 E0→E1 the establishment of reference space rectangular coordinate system |
从E0椭球参心空间直角坐标到E1椭球参心空间直角坐标的转换,主要经过2个步骤:第一,E0椭球上的大地坐标(B, l, H)到E0参心空间直角坐标系的坐标(X, Y, Z)的转换;第二,通过旋转,E0参心空间直角坐标系的坐标(X, Y, Z)向E1参心空间直角坐标系的坐标(X1, Y1, Z1)的转换。经过以上2步,就可以实现E0→E1参心空间直角坐标系的转换,转换模型为[18]
| $ {\left[{{X_1}\;\;{Y_1}\;\;{Z_1}} \right]^{\rm{T}}} = J{\left[{X\;\;Y\;\;Z} \right]^{\rm{T}}}。$ | (6) |
式(6)中,(X1, Y1, Z1)为E1参心空间直角坐标系的坐标,J为E0→E1参心空间直角坐标系的旋转矩阵,(X, Y, Z)为E0参心空间直角坐标系的坐标。
需要说明的是,E0参心空间直角坐标系通过旋转矩阵J转换到E1参心空间直角坐标系之后,X1轴可能会出现2种情况:当X1轴指向线路测区时,解得测点相对于E1椭球的经差很小,可直接按照式(6)计算;当X1轴反向指向线路测区时,解得测点相对于E1椭球的经差的绝对值接近π,由于不方便高斯投影公式的运用,需将该空间直角坐标系绕Z1轴旋转180°作为E1参心空间直角坐标系,根据三个方向分量指向,令G=diag[-1 -1 1]。则给出更为合适的转换公式
| $ {\left[{{X_1}\;\;{Y_1}\;\;{Z_1}} \right]^{\rm{T}}} = \mathit{\boldsymbol{G}}J{\left[{X\;\;Y\;\;Z} \right]^{\rm{T}}}, $ | (7) |
如图 3中,第1步,第2步,第3步的计算方法和具体推导公式以及椭球E1的参数计算公式参考文献[18]。
如果直接对E1椭球进行高斯投影,由于测区内各点在该椭球内大地高较大,必然导致投影之后长度综合变形值较大。从椭球变形法的相关理论进行分析,从而可以得到点在E2椭球上的大地坐标表达式为[18]
| $ \left. \begin{array}{l} {B_2} = {B_1} + \frac{{{K_1}{e_1}^2{\rm{sin}}{B_1}{\rm{cos}}{B_1}}}{{a{\rm{ }}({M_1} + \Delta H)}}{\rm{d}}a + \frac{{{M_1}}}{{({M_1} + \Delta H)(1-{f_1})}}\cdot{\rm{sin}}{B_1}{\rm{cos}}{B_1}(2-{e_1}^2{\rm{si}}{{\rm{n}}^2}{B_1}){\rm{d}}f\\ {l_2} = {l_1}\\ {H_2} = {H_1}-\frac{{{K_1}(1 - {e_1}^2{\rm{si}}{{\rm{n}}^2}{B_1})}}{a}{\rm{d}}a + \frac{{{M_1}(1 - {e_1}^2{\rm{si}}{{\rm{n}}^2}{B_1})}}{{1 - {f_1}}}{\rm{si}}{{\rm{n}}^2}{B_1}{\rm{d}}f \end{array} \right\}, $ | (8) |
式中
| $ \left. \begin{array}{l} {\rm{d}}a = ({W_{\rm{s}}} + \Delta H)\sqrt {1-\frac{{{W_{\rm{s}}}}}{{{W_{\rm{s}}} + \Delta H}}{e_1}^2{\rm{sin}}{B_{\rm{s}}}}-a, \\ {\rm{d}}f = 1-\sqrt {1 - \frac{{{W_{\rm{s}}}}}{{{W_{\rm{s}}} + \Delta H}}{e_1}^2} - {f_1} \end{array} \right\}, $ | (9) |
式中:da,df,ΔH分别表示从E1椭球到E2椭球变换前后的长半径变化量、扁率变化量、基准点处的大地高变化量;f1是E1椭球的扁率;Bs是基准点在E1椭球上的纬度;Ws是测区基准点所对应的卯酉圈曲率半径;K1是E1椭球的卯酉圈曲率半径;M1是E1椭球的子午圈曲率半径。
3 E2椭球高斯投影方法“E2椭球高斯投影方法”的定义为:投影椭球为椭球E2,并以椭球E2的中央子午线为纵轴,与传统高斯投影方法一致进行投影,工程椭球高斯投影方法也属于等角切椭圆柱投影。投影时,所采用的椭球参数是椭球E2的几何参数[18],从而实现椭球E2上大地坐标到平面坐标的转换[22]。其计算公式为
| $ \left. \begin{array}{l} {X_2} = {X_s} + \frac{W}{{2\rho '{'^2}}}{\rm{sin}}{B_2}\Delta {l_2}^2 + \frac{W}{{24\rho '{'^4}}}{\rm{sin}}{B_2}{\rm{co}}{{\rm{s}}^3}{B_2}(5-{t^2} + 9{\eta ^2} + 4{\eta ^4})\Delta {l_2}^4 + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{W}{{720\rho '{'^6}}}{\rm{sin}}{B_2}{\rm{co}}{{\rm{s}}^5}{B_2}(61-58{t^2} + {t^4})\Delta {l_2}^6, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{Y_2} = \frac{W}{{\rho ''}}{\rm{cos}}{B_2}\Delta {l_2} + \frac{W}{{6\rho '{'^3}}}{\rm{co}}{{\rm{s}}^3}{B_2}(1-{t^2} + {\eta ^2})\Delta {l_2}^3 + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{W}{{120\rho '{'^5}}}{\rm{co}}{{\rm{s}}^5}{B_2}(5 - 18{t^2} + {t^4} + 14{\eta ^2} - 58{\eta ^2}{t^2})\Delta {l_2}^5, \end{array} \right\} $ | (10) |
式中:X2,Y2为E2椭球投影后的高斯平面坐标,Xs为E2椭球的纬度B2对应的中央子午线上的弧长,W为E2椭球卯酉圈曲率半径,Δl2为经差(Δl2=l2-l0,l0为中央子午线经度),t=tan B2,η=e′22cos B2(e′22为E2椭球第二偏心率平方)。
需要强调的是,由于式(10)不适用于大地纬度B1→π/2的情况,当测区位于椭球E2的极区位置时,可借助极区非奇异高斯投影复变函数表示式进行计算[23]。
4 算例分析 4.1 椭球参数和旋转矩阵计算测区路线呈东西跨度且长达600 km,位于东经95°00′E-104°30′E,北纬39°00′N-45°00′N。坐标系统:采用2000国家大地坐标系,椭球参数(长半轴a=6 378 137 m,扁率f=298.257 222 101),按高斯投影的方法建立工程独立坐标系,边长综合投影变形值要求小于2.5 cm/km。高程基准:采用1985国家高程基准。测区略图见图 4。
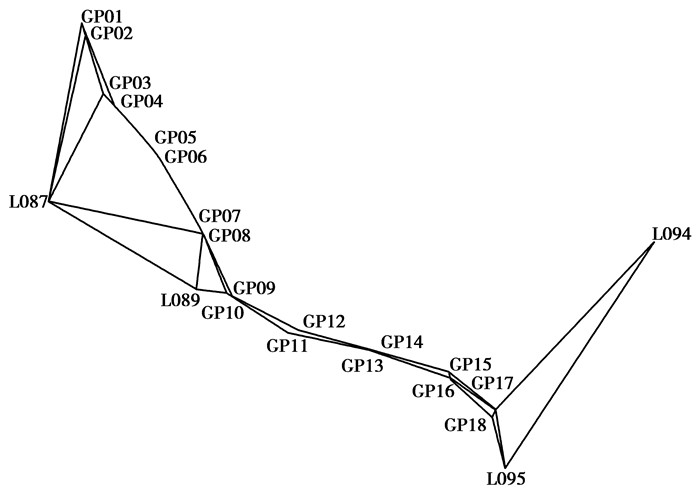
|
图 4 测区略图 Figure 4 Sketch map of survey area |
要实现E0→E1参心空间直角坐标系的转换,关键就是求出它们之间的旋转矩阵。当某一截面椭圆与测区高铁线路在E0椭球上的分布靠近,可以设截面椭圆QMQ′的法向量为φ=[p q 1]。通过计算,p=-0.634 72380,q=-0.779 87994。Q在E0椭球上的大地坐标为(45°31′30.29″,51°06′24.39″,0),E1椭球的短半轴b1=6 367 293.564 001 42,E1椭球的第一偏心率e1=0.058 286 247 16。
计算得到,E0椭球到E1椭球的参心空间直角坐标系的旋转矩阵为
| $ \mathit{\boldsymbol{G = }}\left[{\begin{array}{*{20}{c}} {-0.788{\rm{ }}698}&{0.611{\rm{ }}731}&0\\ {-0.423{\rm{ }}082}&{-0.561{\rm{ }}571}&{0.701{\rm{ }}083}\\ {0.431{\rm{ }}881}&{0.557{\rm{ }}941}&{0.713{\rm{ }}107} \end{array}} \right]。$ | (11) |
取基准点处的纬度Bs=55.8°,ΔH=2 915 m,将E1椭球投影到E2椭球上,计算出E2椭球的第一偏心率e2=0.058 271 984 03。
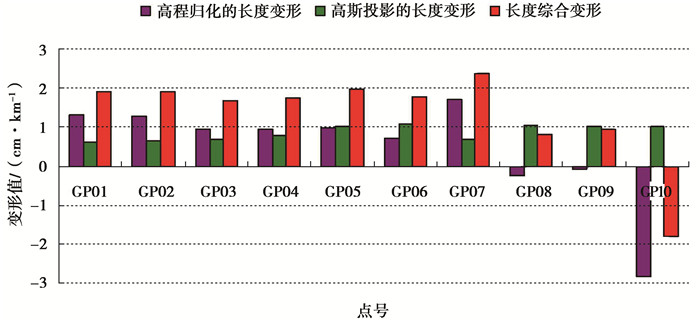
4.2 E2椭球高斯投影方法计算“E2椭球高斯投影方法”计算的各点长度投影变形数据和长度投影变形统计见(表 1和图 5)所示。通过计算,E2椭球与测区最左端的经差为-19′30.462″,中央子午线与测区最左端的距离为-18.5 km,E2椭球与测区最右端的经差为11′37.023″,中央子午线与测区最右端的距离为10.1 km。从表 1和图 5可知,在测区内,高程归化长度变形值的绝对值最大值为2.83 cm/km,高斯投影的长度变形值最大值为1.07 cm/km,长度综合变形的最大值为2.37 cm/km,整条线路各点的综合长度变形值均小于2.5 cm/km[24],因此满足规范要求的允许值。
| 表 1 “E2椭球高斯投影方法”的各点长度投影变形结果 Table 1 The deformation results of each site of "E2 ellipsoid Gauss projection method" |
|
图 5 各点长度投影变形统计图 Figure 5 Projection deformation statistics of the length of each point |
1) 若采用“调整中央子午线”的方法,设中央子午线的值为103°,则投影变形的最大值为232.5 mm;中央子午线与测区的最大距离值为-242.5 km。
2) 若采用“抵偿投影面高斯投影”的方法,通过抬高或抬低投影面,设投影面高程的值为2 900 m,则投影变形的最大值为677.298 mm;中央子午线与测区的最大距离值为-248.5 km。
从以上两种方法的分析结果可以看出,两种方法都无法满足工程规范的要求,要满足限差要求要将全线分为20个带。
3) 若采用本文方法,无需进行多次换带,全线只需1个带就能满足工程要求,并且投影变形值显著减小。
5 结论论述了建立工程椭球的具体思路、流程和方法,并对高铁线路的实际案例进行分析,得出了以下结论:
1) 建立的工程椭球特别适用于东西跨度较大的条带测区,避免了实际工作中高斯投影变形过大需要频繁分带的现象,可以有效避免因分带带来的误差和有效降低高差带来的影响,减少了投影综合变形。
2) 本文方法的优势是,通过抬高或抬低投影面,以及使中央子午线倾斜,对高程归化改正和高斯投影变形两方面的改善效果比较显著,这样建立工程椭球的方法具有实际应用价值。
3) 可以大大减少测区的高斯投影横坐标,使得测区位于一个高斯投影条带内。当测区线路有比较大的弯转,若要保证投影后变形值较小,可以对线路弯转大的地方进行分段处理。
| [1] |
李祖锋, 赵彦华, 巨天灵.
限制GPS边长综合投影变形加权尺度比算法[J]. 工程勘察, 2010, 38(7): 76–79.
LI Zufeng, ZHAO Yanhua, JU Tianling. A weighted scaling-ratio algorithm for reducing the integrated GPS side length projection deformation[J]. Geotechnical Investigation & Surveying, 2010, 38(7): 76–79. (in Chinese) |
| [2] |
李祖锋.
限制边长投影变形最佳抵偿投影面的确定[J]. 工程勘察, 2010, 38(2): 75–78.
LI Zufeng. Determination of optimal compensation projecting plane for restrictions of the length projection deformation[J]. Geotechnical Investigation & Surveying, 2010, 38(2): 75–78. (in Chinese) |
| [3] |
梁海文, 史成梅, 李旭强, 等.
削弱道路勘测放线中投影变形的允差分析法[J]. 测绘通报, 2015(2): 84–87.
LIANG Haiwen, SHI Chengmei, LI Xuqiang, et al. Analysis of allowable error for weakening projection deformation in road setting-out survey[J]. Bulletin of Surveying and Mapping, 2015(2): 84–87. (in Chinese) |
| [4] |
李沛鸿, 王富麒, 刘陶胜.
长距离线路工程投影变形值控制方法分析[J]. 江西理工大学学报, 2012, 33(3): 34–37.
LI Peihong, WANG Fulin, LIU Taosheng. Analysis of deformation control on long-distance projection[J]. Journal of Jiangxi University of Science and Technology, 2012, 33(3): 34–37. (in Chinese) |
| [5] |
杨志, 覃辉, 文鸿雁, 等.
基于投影变形大小的投影带和投影面选择[J]. 公路工程, 2016, 41(1): 59–63.
YANG Zhi, QIN Hui, WEN Hongyan, et al. The selection of projection zone and plane is based on the size of projection distortion[J]. Highway Engineering, 2016, 41(1): 59–63. (in Chinese) |
| [6] |
李邱林, 董武钟, 龚秋全.
基于高海拔地区大型光伏电厂GPS控制网投影变形问题的应用研究[J]. 测绘与空间地理信息, 2016, 39(9): 80–82, 85.
LI Qiulin, DONG Wuzhong, GONG Qiuquan, et al. The research of GPS control network projection deformation of large-scale photovoltaic power plants in high altitude localities[J]. Geomatics & Spatial Information Technology, 2016, 39(9): 80–82, 85. (in Chinese) |
| [7] |
尹晖, 李小祥, 甘喆渊.
椭球变换法建立地方独立坐标系的变形研究[J]. 测绘工程, 2016, 25(2): 1–5.
YIN Hui, LI Xiaoxiang, GAN Zheyuan. Deformation of local independent coordinate established with ellipsoid transform method[J]. Engineering of Surveying and Mapping, 2016, 25(2): 1–5. (in Chinese) |
| [8] |
焦明连.
矿区GPS控制网投影变形的处理[J]. 矿业工程, 2007, 5(2): 72–74.
JIAO Minglian. Projection deformation processing for mine GPS control network[J]. Mining Engineering, 2007, 5(2): 72–74. (in Chinese) |
| [9] |
李祖锋, 高建军, 缪志选, 等.
利用最优抵偿投影面算法限制GPS边长投影变形[J]. 测绘工程, 2010, 19(1): 75–77.
LI Zufeng, GAO Jianjun, MIU Zhixuan, et al. Study on the controlling of GPS length projection deformation with the calculation of optimal compensation projecting plane[J]. Engineering of Surveying and Mapping, 2010, 19(1): 75–77. (in Chinese) |
| [10] |
刘杨, 周世健, 朱煜峰.
相山铀矿田矿区E级GPS控制网投影变形的探讨[J]. 江西科学, 2011, 29(2): 197–199, 215.
LIU Yang, ZHOU Shijian, ZHU Yufeng. Discussion on the projection distortion of E-class GPS surveying control network of Xiangshan uranium mine area[J]. Jiangxi Science, 2011, 29(2): 197–199, 215. (in Chinese) |
| [11] |
冯光东, 王鹏.
高速铁路GPS控制网投影变形处理方法的探讨[J]. 铁道勘察, 2011, 37(1): 4–8.
FENG Guangdong, WANG Peng. Discussion on projection distortion methods of GPS control network on high speed railway[J]. Railway Investigation and Surveying, 2011, 37(1): 4–8. (in Chinese) |
| [12] |
余鹏, 郑健.
高速铁路CPⅢ平面控制网长度投影变形处理方法研究[J]. 铁道勘察, 2011, 37(5): 22–24.
YU Peng, ZHENG Jian. Research on processing length projective deformations for CPⅢ plane network of high-speed railways[J]. Railway Investigation and Surveying, 2011, 37(5): 22–24. (in Chinese) |
| [13] |
于亚杰, 赵英志, 张月华.
基于椭球膨胀法实现独立坐标系统的建立[J]. 测绘通报, 2011(12): 33–36.
YU Yajie, ZHAO Yingzhi, ZHANG Yuehua. The establishment of independent coordinate system based on ellipsoid expansion method[J]. Bulletin of Surveying and Mapping, 2011(12): 33–36. (in Chinese) |
| [14] |
张运华.
高速铁路工程投影变形量的控制[J]. 铁道勘测与设计, 2009(5): 1–3.
ZHANG Yunhua. Control of projection deformation in high speed railway engineering[J]. Railway Survey and Design, 2009(5): 1–3. (in Chinese) |
| [15] |
杨柳.
高铁测量中的投影变形处理方法探讨[J]. 北京测绘, 2012(1): 44–46.
YANG Liu. Discussion of projection deformation processing methods on high railway survey[J]. Beijing Surveying and Mapping, 2012(1): 44–46. (in Chinese) |
| [16] |
金立新. 法截面子午线椭球高斯投影理论: 高速铁路坐标系统投影变形控制理论与应用研究[D]. 北京: 北京交通大学, 2012. JIN Lixin. Gaussian projection theory based on ellipsoid with normal section as the central meridian: Theory and application of projection deformation in high speed railway coordinates system design[D]. Beijing: Beijing Jiaotong University, 2012. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2428391 |
| [17] |
布金伟, 左小清, 常军, 等.
长线路工程法截面子午线椭球建立方法研究[J]. 工程勘察, 2017, 45(8): 48–55.
BU Jinwei, ZUO Xiaoqing, CHANG Jun, et al. Research on the method of establishing normal section meridian ellipsoid for long line engineering[J]. Geotechnical Investigation & Surveying, 2017, 45(8): 48–55. (in Chinese) |
| [18] |
边少锋, 刘强, 李忠美, 等.
斜轴变形椭球高斯投影方法[J]. 测绘学报, 2015, 44(10): 1071–1077.
BIAN Shaofeng, LIU Qiang, LI Zhongmei, et al. An alteration of Gauss projection based on oblique deformed ellipsoid[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1071–1077. (in Chinese) |
| [19] |
金立新, 付宏平. 法截面子午线椭球高斯投影理论[M]. 西安: 西安地图出版社, 2012.
JIN Lixin, FU Hongping. Gaussian projection theory based on ellipsoid with normal section as the central meridian[M]. Xi'an: Xi'an Maps Press, 2012. (in Chinese) |
| [20] |
金立新, 付宏平, 陈向阳. 法截面子午线椭球空间几何理论[M]. 西安: 西安地图出版社, 2013.
JIN Lixin, FU Hongping, CHEN Xiangyang. Spatial geometry theory based on ellipsoid with normal section as the central meridian[M]. Xi'an: Xi'an Maps Press, 2013. (in Chinese) |
| [21] |
金立新, 付宏平. 法截面子午线椭球工程应用研究[M]. 西安: 西安地图出版社, 2017.
JIN Lixin, FU Hongping. Engineering application based on ellipsoid with normal section as the central meridian[M]. Xi'an: Xi'an Maps Press, 2017. (in Chinese) |
| [22] |
孔云祥, 郭际明. 控制测量学:下册[M]. 第三版. 武汉: 武汉大学出版社, 2006.
KONG Yunxiang, GUO Jiming. Control surveying:Volume Ⅱ[M]. 3rd edition. Wuhan: Wuhan University Press, 2006. (in Chinese) |
| [23] |
边少锋, 李忠美, 李厚朴.
极区非奇异高斯投影复变函数表示[J]. 测绘学报, 2014, 43(4): 348–352.
BIAN Shaofeng, LI Zhongmei, LI Houpu. The non-singular formula of Gauss projection in polar regions by complex numbers[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 348–352. (in Chinese) |
| [24] |
中国有色金属工业协会. 工程测量规范: GB50026-2007[S]. 北京: 中国计划出版社, 2008. China Nonferrous Metals Industry Association. Code for Engineering Surveying: GB50026-2007[S]. Beijing: People's Republic of China national standard. Beijing: China Planning Press, 2008. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41


