无线传感器网络(WSN, wireless sensor network)中存在大量传感器节点,其中每个节点的位置均会直接影响WSN的感知能力和工作效率,只有合理部署各节点的位置才能保证WSN对目标区域进行高效稳定的监测[1-3]。因此WSN节点部署算法研究对WSN的发展具有重要意义。文献[4]将混沌算法与粒子群算法相结合,增强粒子群逃逸局部最优的能力,但运用此种方法收敛速度和平均覆盖率均不理想。文献[5]针对WSN节点分布优化问题,以果蝇算法为基础,改进气味函数,使其更好地应用于点覆盖。但此算法中的目标函数需要对ω进行设定,不同的ω对WSN的优化效果有较大影响。文献[6]所用算法吸取了粒子群算法与协同进化算法的优势,进一步增强搜索进化能力,由于每次变异交叉操作均采用简单的随机方式,因此搜索效率低,寻优速度较慢。文献[7]采用人工蜂群算法对WSN部署方案进行制定,所得方案覆盖率高,但收敛速度过慢。文献[8]将差分进化算法与蜂群算法相结合,增强蜜蜂的搜索能力,可以在短时间内获取最佳部署方案。
为了更好地优化WSN节点分布,采用覆盖率较高的传统人工蜂群算法(ABC,artificial bee colony)作为基础算法,再借鉴贝叶斯预测算法的思想,在收敛速度方面进行改进,提出贝叶斯预测人工蜂群算法(BPABC, Bayesian prediction artificial bee colony algorithm),并应用此算法制定节点分布方案,再与传统蜂群算法及全局引导蜂群算法(GABC, global artificial bee colony)的优化方案进行对比,以验证BPABC算法的优越性。
1 问题描述在实际应用中,最简单的WSN节点分布方法是随机部署,这种方式会出现大量重复覆盖的区域,造成资源浪费,无法完成预定的监测任务。而经过优化后的部署方案,可以使WSN最大限度地覆盖监测区域。因此,WSN的节点分布情况会直接影响其对目标区域的监测效果,合理部署其中各节点可以提升WSN的工作性能以及监测能力。此问题具体模型描述如下[9-11]:
设存在二维监测区域A,用于目标区域的WSN中存在N个传感器节点,每个节点的感知半径都是r,所有节点可记为{s1, s2, …, sN}。(xi, yi)代表节点si在区域A中的位置坐标。为了方便计算覆盖率,将目标区域A离散成m×n个点pj,其中m、n分别为横纵坐标的离散点总数,任意点的坐标为(x, y)。定义节点si与离散点pj之间的距离为
| $ d({s_i}, {p_j}) = \sqrt {{{({x_i}-x)}^2} + {{({y_i}-y)}^2}} 。$ | (1) |
根据实际应用情况,采用传感器感知概率模型为
| $ P\{ {s_i}, {p_j}\} = \left\{ {\begin{array}{*{20}{c}} {1, }&{d({s_i}, p) \leqslant r, } \\ {{{\rm{e}}^{-qd({s_i}, p)}}, }&{{{\rm{e}}^{-qd({s_i}, p)}} > \theta, } \\ {0, }&{{{\rm{e}}^{-qd({s_i}, p)}} < \theta, } \end{array}} \right. $ | (2) |
式中:P{si, pj}为节点si能够感知到离散点pj的概率,θ为感知极限,q为传感器感知性能衰减速率。当节点与离散点之间的距离小于感知半径,则感知概率恒为1;反之,感知概率会以指数方式减小直至为0。由于WSN中节点之间的感知概率互为独立,因此综合每个节点的状态即可确定对应离散点能否被有效监测,此时概率可表示为
| $ {P_j} = P(\bigcup\limits_{i = 1}^N P \{ {s_i}, {p_j}\} ) = 1-\prod\limits_{i = 1}^N {(1-P\{ {s_i}, {p_j}\} )}, $ | (3) |
式中:Pj为某离散点pj被传感器网络感知到的概率。
综合考虑每个离散点的被感知概率即可掌握WSN对目标区域的监测情况,为了清晰地反映WSN的感知能力,将能所有被感知的点与所有离散点的比值定义为WSN的覆盖率
| $ Z = \frac{{\sum\limits_{j = 1}^{m \times n} {{P_j}} }}{{m \times n}}。$ | (4) |
WSN节点优化问题就是将网络中的每个节点放置在最合适的位置,使网络覆盖率最大化。由此可见,算法的适应度函数应该定义为
| $ f\left( x \right) = {\text{max}}\left( Z \right) = {\text{max}}(\frac{{\sum\limits_{j = 1}^{m \times n} {{P_j}} }}{{m \times n}})。$ | (5) |
人工蜂群算法(ABC,artificial bee colony a lgorithm)是仿照蜜蜂种群中各蜜蜂之间协作搜寻蜜源的过程而演化成的一种智能算法[12]。此种算法将蜂群中的蜜蜂划分为雇佣蜂、跟随蜂、侦查蜂3类。3种蜜蜂相互配合搜索最优蜜源。算法中的蜜源为优化问题的可行解。
ABC算法中设蜂群的规模为P,其中每个个体均含有d个元素,且定义Xminj与Xmaxj(j=1, 2, …, d)为每个元素的上、下极限值。X(t)=(X1, t, X2, t, …, XP, t)为经过t次迭代后的蜂群,t=1, 2, …, Gmax,其中Gmax为最大迭代次数。在传统ABC算法中,雇佣蜂与跟随蜂数量均为P/2,侦查蜂的数量是根据算法运行状况而确定[13-15]。
ABC算法初始化为
| $ x_{_i}^{^j} = x_{_{{\text{min}}}}^{^j} + \alpha (x_{_{{\text{max}}}}^{^j}-x_{_{{\text{min}}}}^{^j}), $ | (6) |
式中:xij为第i个蜜源的第j个元素,i=1, 2, …, P/2,j=1, 2, …, d;α在0~1的随机数。
雇佣蜂的更新为
| $ v_{_i}^{^j} = x_{_i}^{^j} + \omega (x_{_i}^{^j}-x_{_k}^{^j}), $ | (7) |
式中:xkj为第k个蜜源的第j个元素,k=1, 2, …, P/2,且k≠i;ω为-1~1的随机数。再通过计算目标函数的函数值来评价对比蜜源的质量,并进行优劣更替。
传统ABC算法采用轮盘赌概率法反映各蜜源的状态,跟随蜂以此为依据对蜜源进行搜索更新。若算法运行过程中某一蜜源的局部搜索次数达到l(l为单个蜜源的最大搜索次数),则认为在这个蜜源的邻域内不存在适应度更好的蜜源,侦查蜂将舍弃该蜜源并按照式(6)重新获取新蜜源。
通过以上的分析可以得出,由于传统人工蜂群算法每次搜索只改变一个维度的元素,因此需要大量的迭代才能找到最优解,导致收敛速度过慢。除此之外,每次搜索都是以单纯的随机函数方式对元素进行更新,导致在搜索过程中产生大量较差的可行解,浪费计算资源,降低搜索效率。
3 贝叶斯预测人工蜂群算法针对传统蜂群算法搜索效率低,收敛速度慢等缺陷,文中算法借鉴文献[16]中的贝叶斯预测算法思想,对蜂群算法进行改进。首先需要对传统蜂群算法中的蜂群数量进行调整,在传统蜂群算法中,雇佣蜂和跟随蜂的数量是相等的,以满足所有蜜源的更新需求。在此算法中,设置少量初始雇佣蜂,其数量为a。雇佣蜂的更新公式与传统蜂群算法相同。跟随蜂的数量为b,其包括两部分:一部分用于局部搜索(b1);另一部分在搜索过程中当满足一定条件可转化为雇佣蜂(b2)。
贝叶斯预测算法的思想是根据先前经验与当前计算获得的信息预测问题每个分量存在最优解的概率。为了更准确地预测各雇佣蜂对应蜜源邻域存在最优解的概率,在BPABC算法设置先验概率与后验概率,其中先验概率Vt-1[n]是指前一次迭代各蜜源对应存在最优解的概率,后验概率是通过计算当前各蜜源对目标区域的覆盖率,并按照轮盘赌的方式获得各蜜源附近邻域存在最优解的概率。第t代的预测概率的获取是以先验概率为基础,在根据后验概率对其进行修正调整。其具体更新公式为
| $ {V_t}\left[n \right] = \frac{{{V_{t - 1}}\left[n \right] \times {P_{t, n}}}}{{\sum\limits_{i = 1}^E {{V_{t - 1}}} \left[i \right] \times {P_{t, j}}}}, $ | (8) |
式中:Vt[n]为第t代、第n个蜜源附近存在最优解的概率;Pt, n则为第t代通过计算得到第n个蜜源的后验概率;E为蜜源的总数,初始时为a,算法运行过程中,E值会变化为(a+ b2)。采用式(8)将算法运行经验与当前数据结合,可以更加客观准确地预测最优解的位置。
跟随蜂搜索环节所有跟随蜂会在预测概率向量Vt的指导下对用于搜索各蜜源的跟随蜂数量进行调整。第t代各蜜源具体分配的跟随蜂数目为
| $ {F_t}\left[i \right] = {V_t}\left[i \right] \times b, $ | (9) |
式中:Ft[i]为第t次迭代时算法指派在第i个蜜源附近搜索的跟随蜂数目,i=1, 2, …, E。在分配跟随蜂的过程中不可避免地会出现跟随蜂数目为小数的现象,算法采取向下取整的原则处理此种情况。依照以上的分配方法会出现少量闲置跟随蜂,此时算法会根据闲置跟随蜂的数量选取等量的未有效搜索蜜源(最优解存在概率小所导致)进行一对一匹配搜索。这样就可以保证跟随蜂的利用率以及算法搜索的全面性。
每只跟随蜂均按照式(10)和式(11)进行更新,
| $ w_{_m}^{^j} = x_{_i}^{^j} + r \times \beta, $ | (10) |
| $ r = 5-4 \times \frac{t}{{{G_{{\text{max}}}}}}, $ | (11) |
式中:wmj为第m个跟随蜂中的第j个元素,m=1, 2, …, Ft[i];xij则为第i个蜜源的第j个元素,i=1, 2, …, E;r为搜索半径;β为-1~1的随机数;t为算法迭代次数。每只跟随蜂均会以目标蜜源为基点,在半径为r的范围内随机取值。将跟随蜂的所有搜索结果与目标蜜源进行对比,适应度函数值最优的结果替换目标蜜源,若对比后目标蜜源的适应度函数值仍为最优,则保留目标蜜源,并且将局部搜索的次数c增加1。
在算法运行过程中,当某个蜜源的预测概率超过50%时,BPABC算法对蜜源划分成2个二级蜜源进行分区搜索,每个蜜源的预测概率均为原来的1/2,并且更新公式不变,只是2个二级蜜源的α取值与先前不同,分别为-1~0和0~1的随机数。筛选每个二级蜜源附近适应度函数值最好的跟随蜂作为新的蜜源,若此蜜源附近所有跟随蜂的结果均不如划分前的蜜源,则保留原来的原蜜源结果与预测概率,局部搜索次数加1。
贝叶斯预测蜂群算法具体运行流程如下:
Step1 初始化。对算法中的各参数进行设定,并初始化雇佣蜂搜索的蜜源,各蜜源的先验概率均设置为1/a。对每个蜜源进行评价并获得后验概率。按照式(6)计算初始蜜源的预测概率向量。
Step2 雇佣蜂环节。雇佣蜂对相应蜜源按照式(7)进行搜索。完成评价后,对所有蜜源和预测概率进行优化更新操作,局部搜索次数c置0。对于不满足更新条件的蜜源,则其局部搜索次数c增加1。
Step3 跟随蜂环节。对照预测概率产生二级蜜源,并根据式(9)对所有跟随蜂进行分配。按照式(10)和式(11)对各蜜源进行搜索,评价,并完成蜜源、局部搜索次数的替换更新工作。统计蜜源以及跟随蜂的数量。
Step4 蜜源淘汰环节。当蜜源的数量超过蜜源数量上限M时,算法按照上一环节所评价的质量,淘汰质量差的蜜源,直至蜜源数量满足要求。随后获取现存蜜源的预测概率向量。并记录全局最优蜜源xbest。
Step5 侦查蜂环节。若某一蜜源的局部搜索次数达到l,侦查蜂会对蜜源重新进行初始化。并更新预测概率向量。
Step6 若全局迭代次数t未到达Gmax,则跳转到Step2;否则,结束算法运行。
4 实验仿真研究采用Matlab编写算法对贝叶斯预测蜂群算法的运行效果进行测试,并对其应用于WSN节点分布优化方面的优越性进行验证。将BPABC、GABC、ABC 3种算法的优化结果进行对比。设WSN中存在60个完全相同的传感器节点,其感知半径皆为20 m。为了突显BPABC的算法性能,因此这里随机对算法的参数进行设定,预设的参数如下:a=20,b=80(其中b1=60,b2=20),l=20,Gmax=500。WSN应用于200 m×200 m的监测区域中。其他2种算法相关参数与上述参数相同,3种算法分别运行200次,运行结果如表 1所示。
| 表 1 3种算法的优化结果对比 Table 1 Comparison of 3 kinds of optimization results |
由表 1可知,经过多次实验,基于BPABC算法的WSN可以覆盖目标区域97%左右的面积,此种算法最差的覆盖结果也可达95%以上。在寻优速度方面,BPABC可以在大约166次时得到最优分布方案。对比其他2种算法可知,BPABC算法在以上这些方面具有明显的优势。3种算法的迭代优化曲线如图 1所示。

|
图 1 3种算法的覆盖率优化曲线图 Figure 1 The curve of coverage optimization of ABC, GABC, BPABC algorithm |
由图 1可知,相比于ABC、GABC算法,BPABC算法能够在最短时间内获取最佳节点分布方案,并且此方案的覆盖率同样优于其他2种算法。除此之外,运用BPABC算法覆盖率大致保持增长趋势,有效地摆脱局部最优的状态。因此,综上所述,应用BPABC算法可以更好地完成节点优化任务。
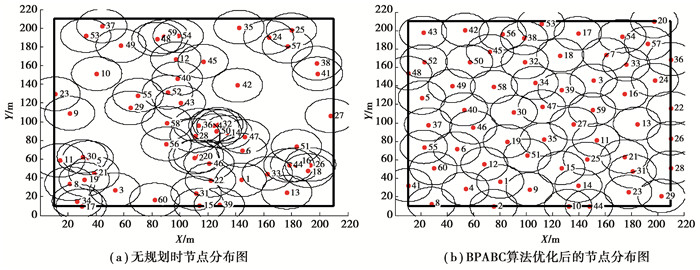
采用BPABC算法制定的WSN节点分布方案如图 2所示。对比2图可知,若不对节点分布进行规划则会出现大量的监测重叠区域(如图 2(a)),降低WSN的工作效率。采用BPABC算法对节点分布进行优化(如图 2(b)),优化结果显示,每个节点分布较为合理,覆盖盲区较少,大幅度提升WSN的监测性能。
|
图 2 基于BPABC算法的节点优化效果图 Figure 2 Node optimization distribution based on BPABC algorithm |
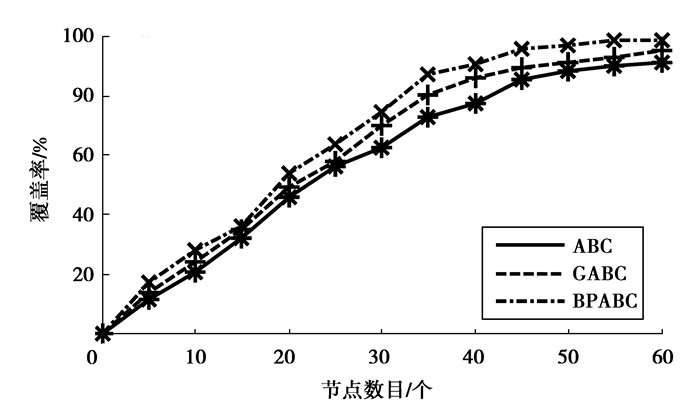
为了进一步检测BPABC算法的性能,采用3种算法对节点数目不同的WSN进行优化,在节点数目不同时,3种算法的覆盖率变化如图 3所示。当WSN中节点不充足时,对比3种算法生成的方案,节点之间的覆盖区域几乎不存在交集,因此3种方案具有相似的覆盖率。3种优化算法的覆盖率随着节点数目的增加而增加,增加速率逐渐变小,但BPABC的优化效果始终优于其他2种,并且当节点数达到60时,BPABC算法的优势体现得更加明显。
|
图 3 ABC、GABC、BPABC算法的覆盖率变化曲线 Figure 3 The curve of coverage based on ABC, GABC, BPABC algorithm |
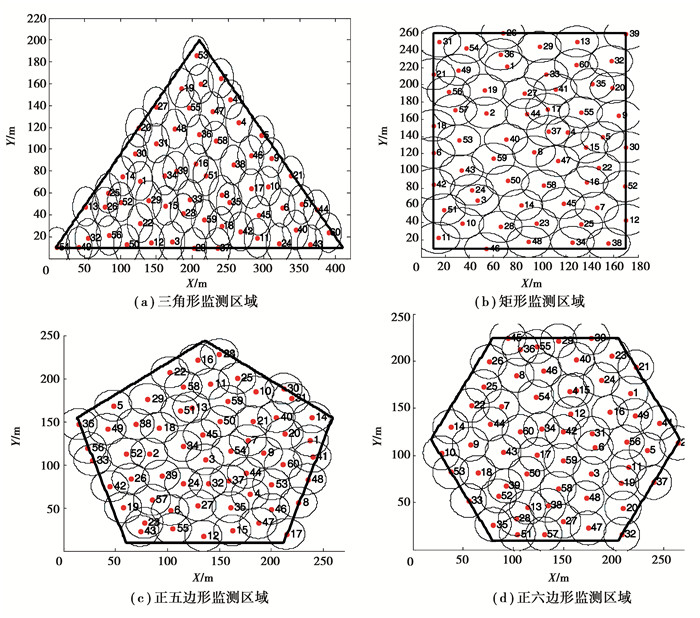
以上分析结果皆针对正四边形监测区域,为了验证文中所用算法的推广价值,将BPABC算法应用于与上述监测面积相同的正三角形、矩形、正五边形、正六边形监测区域。经过算法优化后,各监测区域的节点分布图如图 4所示。
|
图 4 不同监测区域的WSN节点分布方案 Figure 4 WSN node distribution scheme for different monitoring areas |
运用BPABC算法对各监测区域中的节点优化部署200次,运行结果如表 2。
| 表 2 不同监测区域的优化结果对比 Table 2 Comparison of optimization results for different monitoring areas |
根据以上的数据和分布图可知,经过BPABC算法优化后的节点部署方案对各监测区域具有较高的覆盖率,虽然运用ABC、GABC算法同样能实现较均匀部署,但覆盖率方面仍然不如BPABC算法制定的方案。通过仿真对比,BPABC算法对任意区域的平均覆盖率和最差覆盖率均可达到95%以上。且覆盖率的标准差不超过0.005。这说明采用BPABC算法具有很强的适应性和较高的稳定性,在进行节点分布优化时可以不受监测区域形状的影响,只与其面积有关。因此将BPABC算法应用于WSN节点分布优化问题具有一定的推广价值。
5 结论针对WSN网络节点优化问题提出了BPABC算法,此种算法引入贝叶斯预测算法思想,预测人工蜂群算法中各蜜源存在最优解的概率,根据所得的预测结果对各蜜源进行有针对性地搜索,有效地提高了搜索效率。对BPABC算法进行编程仿真,仿真实验表明,BPABC算法可以在较少的迭代次数下获取高覆盖率的节点分布方案,并且对于任意监测区域均可制定满足监测需求的方案,由此可见,算法具有良好的适应性。未来可以根据实际需求在算法中增加其他优化目标函数,使优化后的方案更好地在实际中进行应用。
| [1] | Benatia M A, Sahnoun M, Baudry D, et al. Multi-objective WSN deployment using genetic algorithms under cost, coverage, and connectivity constraints[J]. Wireless Personal Communications, 2017: 1–30. |
| [2] | Yang H, Xunbo L I, Wang Z, et al. A novel sensor deployment method based on image processing and wavelet transform to optimize the surface coverage in WSNs[J]. Chinese Journal of Elecironics, 2016, 25(3): 495–502. DOI:10.1049/cje.2016.05.015 |
| [3] | Cong C. A coverage algorithm for WSN based on the improved PSO[C]//International Conference on Intelligent Transportation, Big Data and Smart City. [S. l. ]: IEEE, 2015: 12-15. |
| [4] |
潘丽姣, 吴红英.
混沌逃逸粒子群优化箅法在WSN盖优化中的应用[J]. 重庆邮电大学学报(自然科学版), 2014, 26(2): 177–181.
PAN Lijiao, WU Hongying. Application of chaotic escape particle swarm optimization algorithm in coverage optimization of wireless sensor networks[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2014, 26(2): 177–181. DOI:10.3979/j.issn.1673-825X.2014.02.007 (in Chinese) |
| [5] |
姚勇涛, 吴雪, 吴喆.
祓于改进的果蝇优化箅法的WSN节点部署设计[J]. 华东理工大学学报(自然科学版), 2016, 42(4): 545–551.
YAO Yongtao, WU Xue, WU Zhe. Wireless sensor network node deployment design based on improved fruit fly optimization algorithm[J]. Journal of East China University of Science and Technology(Natural Science Edition), 2016, 42(4): 545–551. (in Chinese) |
| [6] |
王长清, 黄静.
雄于协同进化粒子群箅法的无线传感器网络节能优化概盖箅法[J]. 河南师范大学学报(自然版), 2016, 44(1): 54–58.
WANG Changqing, HUANG Jing. Energy-saving coverage algorithm for wireless sensor network based on co-cvolutionary particle swarm optimization[J]. Journal of Henan Normal UniversityCNatural Science Edition), 2016, 44(1): 54–58. (in Chinese) |
| [7] | Xu X, Zhou G, Chen T. Research on coverage optimisation of wireless sensor networks based on an artificial bee colony algorithrn[M]. Geneva: Inderscience Publishers, 2015. |
| [8] |
熊伟丽, 刘欣, 陈敏芳, 等.
难于差分蜂群箅法的无线传感器M络节点分布优化[J]. 控制T程, 2014, 21(6): 1036–1040.
XIONG Weili, LIU Xin, CHEN Minfang, et al. Node distribution optimization in wireless sensor networks based on differential bee colony algorithm[J]. Control Engineering of China, 2014, 21(6): 1036–1040. (in Chinese) |
| [9] | Yang H, Li X, Wang Z, et al. A novel sensor deployment method based on image processing and wavelet transform to optimize the surface coverage in WSNs[J]. Chinese Journal of Electronic, 2016, 25(3): 495–502. DOI:10.1049/cje.2016.05.015 |
| [10] | Guo Y N, Cheng J, Liu H Y, et al. A novel knowledge-guided evolutionary scheduling strategy for energy-efficient connected coverage optimization in WSNs[J]. Peer-to-Peer Networking and Applications, 2017, 10(3): 547–558. |
| [11] |
陈树, 钱成.
一种多目标的锻盖优化策略在WSNs中的应用[J]. 传感器与微系统, 2014, 33(10): 151–154.
CHEN Shu, QIAN Cheng. Application of a multi-objective coverage optimization strategy in WSNs[J]. Transducer and Microsystem Technologies, 2014, 33(10): 151–154. (in Chinese) |
| [12] |
朱志洁, 张宏伟, 王春明.
雄于人工蜂群箅法优化支持昀量机的采场底板破坏深度预测[J]. 重庆大学学报:自然科学版, 2015, 38(6): 37–43.
ZHU Zhijie, ZHANG Hongwei, WANG Chunming. Prediction of floor damaged depth in working area based on support vector machine and artificial bee colony algorithm[J]. Journal of Chongqing University, 2015, 38(6): 37–43. (in Chinese) |
| [13] | Kiran M S, Hakli H, Gunduz M, et al. Artificial bee colony algorithm with variable search strategy for continuous optimization[J]. Information Sciences, 2015, 300(S): 140–157. |
| [14] | Brajevic I. Crossover-based artificial bee colony algorithm for constrained optimization problems[J]. Neural Computing 6-Applications, 2015, 26(7): 1587–1601. |
| [15] | Maeda M, Tsuda S. Reduction of artificial bee colony algorithm for global optimization[J]. Neurocomputing, 2015, 148(33): 70–74. |
| [16] |
姜允志, 郝志峰, 张宇山, 等.
贝叶斯预测型进化算法[J]. 计算机学报, 2014, 37(8): 1846–1858.
JIANG Yunzhi, HAO Zhifeng, ZHANG Yushan, et al. Bayesian forecasting evolutionary algorithm[J]. Chinese Journal of Computers, 2014, 37(8): 1846–1858. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41

