2. 武汉第二船舶设计研究所, 武汉 430205;
3. 重庆大学 航空航天学院, 重庆 400044
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, P. R. China;
3. College of Aerospace Engineering, Chongqing University, Chongqing 400044, P. R. China
了解和预测薄膜表面的形态产生和形貌演化对物理学、生物学[1-5]以及工程领域具有重要的意义[6-10]。无论是自由薄膜(无基底)或者是液体基底-薄膜及固体基底-薄膜的弹性失稳研究均引起了人们的极大关注。例如,对于自由薄膜,Coman等[11]研究了环状薄膜在张力下的失稳;Klein等[12]研究了由于侧边的不均匀收缩导致的凝胶薄片的大尺度失稳及局部褶皱。现在被广泛研究的有附着于弹性基底的失稳薄膜,例如膨胀的凝胶薄膜[13]、受压缩的硬膜[14]和局部生长的薄片[15],还有液体表面的薄膜。液体表面的薄膜这种结构出现在很多情况下[16],如肺泡液-空气界面[17]的人肺表面活性剂(由脂质和蛋白质组成的薄膜),以及在液体表面的纳米颗粒膜[18]和厚度为10 μm的聚酯膜[19]。
已有不少学者建立了多种理论模型,从不同的角度对液体表面薄膜的失稳问题进行研究[16, 19-24]。例如,Pocivavsek等[19]引入标度律研究了膜的起皱和折叠状态,结果表明,周期褶皱只是薄膜失稳的一种可能形态;当薄膜两端的压缩量超过其初始失稳波长的三分之一时,局部的褶皱形貌将会出现。Brau等[16]给出了无限长薄膜从全局失稳到局部失稳的理论解。由于实验中只能使用有限长的薄膜进行观测,因此有些理论研究[20-21]考虑了薄膜长度的影响,以缩小与实验结果的差异。
现有的研究主要集中于探讨无缺陷薄膜的失稳问题。然而,实际中薄膜可能存在几何形状和材料性质等方面的缺陷。相较于固体基底,液体基底情况下的薄膜在受到面内压缩过程中,其失稳过程对于缺陷更加敏感。由于薄膜中缺陷的存在,其表面可能会产生更丰富的形态。缺陷对液体基底-薄膜失稳过程的影响仍然缺乏系统的研究。另外,由于所得到的形貌均为弹性失稳,即使卸载后,薄膜仍回复到初始状态,因此,有必要将所得到的形貌进行复制以利于应用。
文中对液体基底情况下表面含有缺陷的弹性薄膜进行有限元模拟和实验研究,探讨不同形式的缺陷对薄膜失稳的影响,并利用模具胶对失稳形貌进行复制。文章主要分为以下几个章节:第1节给出文中所研究的薄膜模型,并通过有限元模拟进行研究。第2节主要通过实验方法得到PET薄膜的失稳规律,并将失稳形貌复制到模具胶表面。第3节对研究工作进行总结。
1 有限元模拟考虑图 1所示的液体表面非均匀薄膜在面内压缩载荷作用下的失稳问题。赋予中间部分薄膜不同于两侧区域的材料属性,从而引入薄膜的非均匀性。图中L2部分与薄膜其余部分的材料属性不同,因此可以将其视为缺陷。假定薄膜各部分均为各向同性线弹性均匀材料。左右边界施加沿水平方向给定的压缩位移边界条件,薄膜的下表面受到液体基底的支撑作用,上表面为自由边界。

|
图 1 液体基底-薄膜系统在面内受压的模型示意图 Figure 1 Schematic of a fluid-supported inhomogeneous film under compression |
采用有限元软件ABAQUS的隐式动态分析方法对液体基底-薄膜系统的失稳过程进行模拟。采用如图 1所示的坐标系,薄膜总长度为L=L1+L2+L3=200 mm,在有限元模拟中选用二次梁单元(B22)对薄膜进行网格划分。液体基底对薄膜的支撑作用定义为施加在梁下表面的压力,其大小p与对应的局部梁挠度y的关系为p=-ρgy,方向始终垂直于梁,其中ρ为水的密度,g为重力加速度。通过改变薄膜缺陷部分的长度L2、位置参数q以及其弹性模量比例参数γ=E2/E1,模拟薄膜的失稳过程,并对模拟的结果进行分析讨论。其中q为缺陷中心水平坐标值与薄膜总长度L的比值,E2为缺陷部分的弹性模量,E1为薄膜其余部分的弹性模量。薄膜的泊松比均取为0.3。
首先,研究弹性模量E2对薄膜失稳过程的影响。选定缺陷部分的长度为L2=5 mm,q=0.5,E1=6 552 MPa。设定3组不同的弹性模量比例参数γ(γ=1/8, 1.0, 8.0),模拟薄膜的失稳形貌,模拟结果如图 2所示。

|
图 2 当L2=5 mm, q=0.5时,3种弹性模量参数下的薄膜失稳有限元模拟形貌图 Figure 2 FEM simulation results of instability pattern on film surface with three different modulus ratio |
如图 2(a)所示,当γ=1/8时,在加载一定压缩位移后,仅薄膜的缺陷部分形成折叠状的初始失稳形貌,并且随着压缩位移的逐渐增大,失稳形貌的幅值也逐渐增大。图 2(b)为无缺陷薄膜(γ=1)的失稳过程。其初始失稳形貌为全局周期性褶皱,随着压缩位移的增大,薄膜在中部形成幅值逐渐增大的折叠形貌,而其余部分的褶皱逐渐消失。在图 2(c)中,当γ=8时,薄膜初始形成全局周期形貌,然后逐渐在缺陷部分的一侧产生屈曲折叠形貌,最终的屈曲折叠形貌出现在缺陷部分的一侧。
由模拟结果可以得出,非均匀薄膜弹性模量参数的变化会在很大程度上影响薄膜的失稳形貌。大量非均匀薄膜的算例验证表明,当γ < 1时,薄膜仅会在缺陷附近产生局部的折叠形貌,而当γ≥1时,薄膜会先产生全局的失稳形貌,进而演化为局部的折叠形貌,如图 3所示。

|
图 3 不同弹性模量参数下薄膜的初始失稳有限元模拟形貌图 Figure 3 FEM simulation results of initial instability pattern on film surface with different modulus ratio |
考虑缺陷部分的宽度和位置因素的算例分析,结果表明,这两个因素不会对薄膜的演化规律产生本质影响,但会影响其局部形貌。其中部分结果将在第2节与实验结果进行对比分析时加以阐述,在此不作赘述。
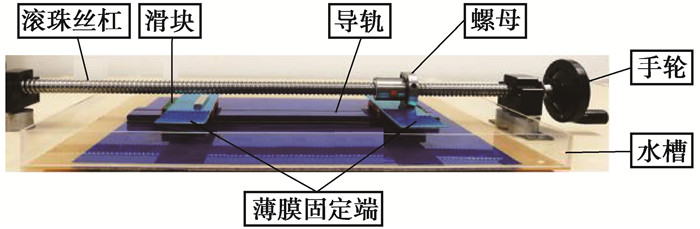
2 液体基底-薄膜位移加载实验为了开展液体基底-薄膜失稳的实验,自制如图 4所示的实验装置,装置主要由滚珠丝杠、滑块导轨副、水槽,以及用于夹持薄膜的铝片等部分组成。实验使用的薄膜为聚酯(PET,Polyethylene terephthalate)薄膜,选用了6 μm、12 μm这2种厚度,长度和宽度分别为200 mm和100 mm。
|
图 4 液体基底-薄膜受压失稳实验装置 Figure 4 Self-designed system for the experiment of a fluid-supported film under compression |
实验中,首先将薄膜两端用铝片夹持并固定于两滑块表面,然后在水槽中加入适量的水并使液面与薄膜下表面齐平,再通过旋转手轮实现薄膜右端的位移加载,同时利用工业相机记录薄膜的失稳过程。
2.1 液体基底-薄膜失稳形貌演化实验 2.1.1 均匀弹性薄膜选用长×宽×厚为200 mm×100 mm×12 μm的PET薄膜,将其固定到实验装置上进行位移加载,实验结果如图 5所示。
|
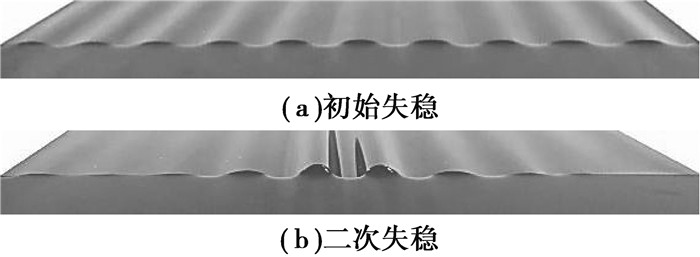
图 5 均匀薄膜失稳实验形貌图 Figure 5 Instability pattern of uniform film in experiment |
如图 5(a)所示,均匀弹性薄膜在压缩过程中首先在全局形成具有类似正弦形状褶皱的失稳形貌;随着压缩位移的增大,薄膜在中部形成幅值逐渐增大的折叠形貌,而其余部分的褶皱则逐渐消失,如图 5(b)所示。该实验结果与图 2(b)中的有限元模拟结果吻合较好。
2.1.2 非均匀薄膜为通过实验探讨缺陷部分的3个参量(弹性模量、长度、位置)对薄膜失稳的影响,首先需要在均匀薄膜表面构建缺陷。要改变缺陷部分的弹性模量,最直接的办法是通过化学手段对薄膜进行表面改性,但不易实施。对于薄膜,其主要的力学参数为薄膜的抗弯刚度Eh3/12,因此可以通过改变薄膜的厚度,以等效薄膜弹性模量的改变,两者在数值上存在3次方的换算关系。当弹性模量比例参数γ>1时,就在缺陷部分增加薄膜厚度,反之,则减少缺陷部分的薄膜厚度。在本次实验中,将均匀薄膜的厚度设定为h,当缺陷部分的厚度增加至2h时,弹性模量比例参数γ=8;当缺陷部分的厚度减小至h/2时,弹性模量参数γ=1/8。在这2种弹性模量取值条件下,再进一步通过改变缺陷部分的长度和位置来观察薄膜的失稳形貌并与模拟结果进行对照,研究缺陷3个属性对失稳形貌的影响规律。
当弹性模量比例参数大于1时,实验中仍选用厚度为12 μm的PET薄膜作为薄膜主体,在其表面加贴一段12 μm的膜以形成缺陷(γ=8)。图 6给出了实验结果,以及相应的有限元模拟结果。
|
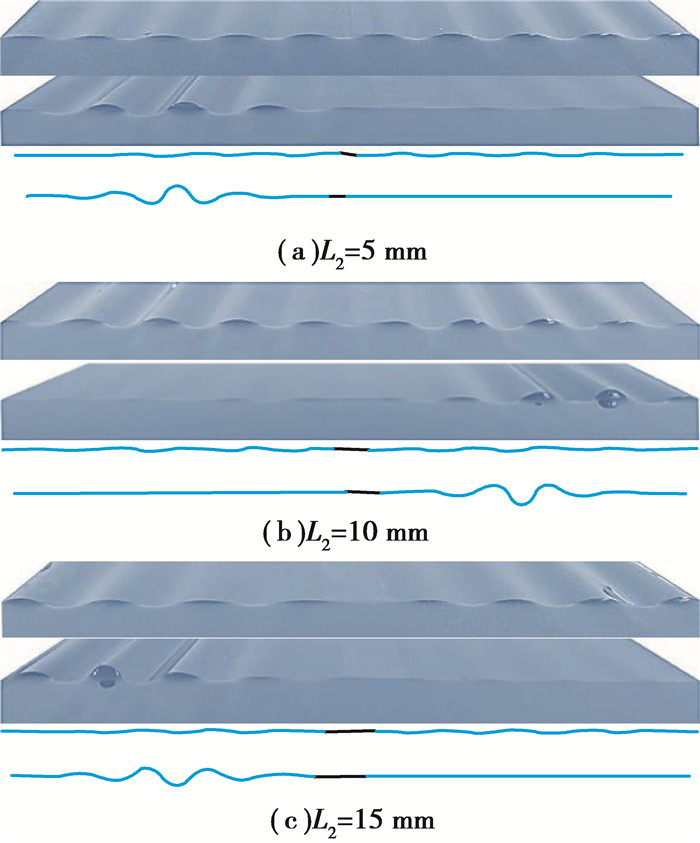
图 6 当γ=8, q=0.5时,实验和有限元模拟得到的带有不同长度缺陷的薄膜失稳形貌对比图 Figure 6 Comparison of film instability patterns by experiments and numerical simulations with different defect length, where γ=8, q=0.5 |
如图 6(a)所示,当L2=5 mm时,非均匀薄膜能在全局形成正弦形状褶皱的初始失稳形貌,与均匀薄膜失稳情况相似,而二次失稳则是发生在缺陷部分的一侧;图 6(b)所示为L2=10 mm的失稳形貌,可以看到由于缺陷部分的长度增大,初始失稳时失稳形貌的幅值在缺陷部分相对减小,而二次失稳同样是发生在缺陷部分的一侧;当L2=15 mm时,由于缺陷部分的长度进一步增大,薄膜初始失稳时缺陷部分的幅值更小,失稳形貌更趋于平坦,但二次失稳形貌与前两种情况依然类似,即出现在缺陷部分的一侧,如图 6(c)所示。从图中可以看出,整个实验结果与有限元模拟结果吻合较好。
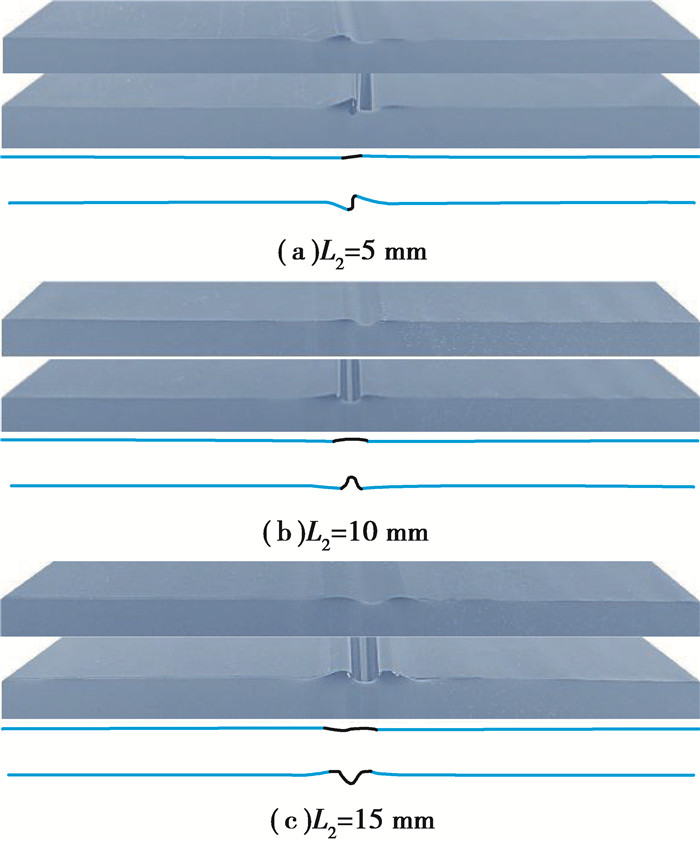
当缺陷的弹性模量比小于1时,实验中选用2片厚度为6 μm的PET薄膜粘叠在一起作为薄膜主体,只是将其中1片薄膜挖去一段以形成缺陷(γ=1/8)。如图 7所示,在不同的缺陷宽度条件下,薄膜均在缺陷处发生初次失稳,不同的是当缺陷宽度为5 mm时是反对称失稳,而缺陷宽度为10 mm和15 mm时是对称失稳,该实验结果和有限元模拟结果吻合。
|
图 7 当γ=1/8, q=0.5时,实验和有限元模拟得到的带有不同长度缺陷的薄膜失稳形貌对比图 Figure 7 Comparison of film instability patterns by experiments and numerical simulations with different defect length, where γ=1/8, q=0.5 |
在γ=1/8和γ=8这2种条件下,继续探讨缺陷部分在薄膜中的位置对薄膜失稳的影响。在有限元模拟和实验中,取缺陷部分长度L2=5 mm,设定3种不同的位置参数q(q=0.125, 0.25, 0.5)进行研究。
结果表明,当γ=1/8时,薄膜中缺陷部分的位置决定着薄膜发生失稳的区域,但基本不影响失稳形貌,与图 7的结果类似;当γ=8时,薄膜首先产生全局失稳,随着压缩位移的增大,其二次失稳形貌出现在缺陷和与其相距较远的端部之间的区域,结果与图 6相似。
以上关于缺陷部分的弹性模量、长度和位置3个参数对薄膜失稳影响的研究表明,缺陷部分弹性模量参数的变化在薄膜失稳行为中起着决定性的作用,其大小决定了薄膜在失稳过程中是否会产生全局性失稳,以及失稳形貌的演化规律。
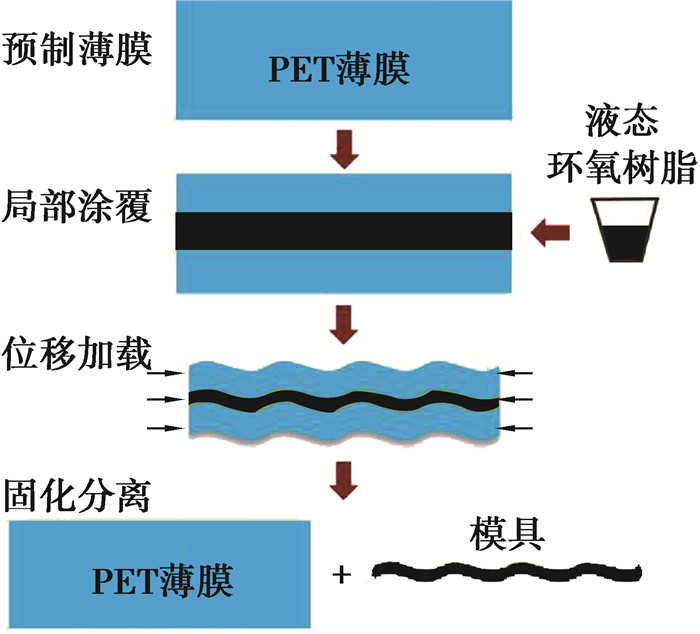
2.2 液体基底-薄膜失稳形貌复制实验 2.2.1 实验原理和步骤在前面的研究中得到了不同类型的失稳形貌。这些失稳形貌均为弹性形变,在外界载荷发生改变时,形貌也会随之产生变化。为了得到稳定的失稳形貌并在以后进行可能的利用,如制备特定形貌的表面,研究进一步采用模具胶将弹性失稳形貌加以复制。实验步骤如图 8所示:①在平整的薄膜表面局部涂覆一层厚度为0.1 mm的模具胶液态环氧树脂;②将预制好的薄膜放置在液面上并在其两端施加位移载荷;③当薄膜表面产生特定的屈曲形貌时,保持此时的位移压缩量;④待表面的环氧树脂完全固化后,将其与PET薄膜进行分离。实验中采用的环氧树脂牌号为DG-3s(中蓝晨光化工设计研究院)。环氧树脂为粘度很高的液体(粘度值为8~10 Pa·s),在薄膜失稳形貌形成过程中,环氧树脂可以在薄膜表面形成较均匀的液体薄层。另外,液体状环氧树脂的弯曲刚度远小于PET薄膜,其对PET薄膜本身失稳形貌的影响可以忽略。
|
图 8 液体表面薄膜失稳形貌复制过程图 Figure 8 The reproducing process of instability pattern on fluid-supported film surface |
通过模具胶复制的方法,最终得到了多种稳定的失稳形貌模具,如图 9和图 10所示。图 9(a)和图 9(b)分别是均匀薄膜的初次失稳和二次失稳形貌模具,其形貌和图 2(b)的有限元模拟结果以及图 5的实验结果均吻合较好,从而也验证了液态环氧树脂层对PET薄膜失稳形貌的影响较小;图 10(a)和图 10(b)分别是参数为γ=8, L2=5 mm, q=0.5和γ=8, L2=5 mm, q=0.25的非均匀薄膜二次失稳形貌模具,其形貌和实验结果(图 6(a))及有限元模拟结果也吻合较好;图 10(c)是参数为γ=1/8, L2=5 mm, q=0.5的非均匀薄膜二次失稳形貌模具,其结果和图 7(a)所示的结果吻合较好。

|
图 9 复制均匀薄膜失稳形貌得到的模具 Figure 9 The molds reproduced by the instability pattern of uniform film |

|
图 10 3组参数情况下复制非均匀薄膜二次局部失稳形貌得到的模具 Figure 10 The molds reproduced by the secondary partial instability pattern of inhomogeneous film under three sets of parameters |
通过数值模拟和实验手段研究了液体表面具有缺陷的薄膜在面内压缩载荷作用下的失稳形貌演化规律,并采用模具胶将弹性失稳形貌加以复制,得到可用于制备特定表面形貌的模具。
1) 有限元模拟结果表明缺陷部分的长度、位置和弹性模量参数都会对薄膜的失稳形貌产生影响。当弹性模量比例参数γ < 1时,薄膜在整个加载过程中只发生局部失稳。缺陷部分的长度决定了薄膜产生对称或反对称失稳形貌,缺陷部分的位置决定了薄膜失稳形貌产生的区域。当弹性模量比例参数γ>1时,缺陷部分长度和位置的改变对薄膜失稳形貌的影响相对较小,薄膜的初始失稳均为全局失稳,后屈曲失稳则在缺陷部分的一侧产生局部折叠形貌。
2) 通过设计制作由滚珠丝杠和滑块导轨副等组成的实验装置,开展液体表面聚酯薄膜的面内压缩实验,得到了不同缺陷参数条件下薄膜的失稳形貌。实验结果与相应的有限元模拟结果吻合较好。
3) 选取环氧树脂模具胶,采用表面复制的方法将特定的失稳形貌完全复制,得到了能方便和稳定制备具有特殊表面形貌的模具。
研究成果有助于理解自然界中某些特定表面形貌的产生机理,并提出了一个进行特定表面形貌设计和制备的简便有效方法,将来可能应用于生物、物理以及超疏水材料等领域。
| [1] | Basan M, Joanny J F, Prost J, et al. Undulation instability of epithelial tissues[J]. Physical Review Letters, 2011, 106(15): 158101. DOI:10.1103/PhysRevLett.106.158101 |
| [2] | Ciarletta P, Amar M B. Growth instabilities and folding in tubular organs: A variational method in non-linear elasticity[J]. International Journal of Non-Linear Mechanics, 2012, 47(2): 248–257. DOI:10.1016/j.ijnonlinmec.2011.05.013 |
| [3] | Goriely A, Geers M G D, Holzapfel G A, et al. Mechanics of the brain: perspectives, challenges, and opportunities[J]. Biomechanics & Modeling in Mechanobiology, 2015, 14(5): 931–965. |
| [4] | Bayly P V, Taber L A, Kroenke C D. Mechanical forces in cerebral cortical folding: A review of measurements and models[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2014, 29(6): 568–581. |
| [5] | Chen X, Yin J. Buckling patterns of thin films on curved compliant substrates with applications to morphogenesis and three-dimensional micro-fabrication[J]. Soft Matter, 2010, 6(22): 5667–5680. DOI:10.1039/c0sm00401d |
| [6] | Cai S, Breid D, Crosby A J, et al. Periodic patterns and energy states of buckled films on compliant substrates[J]. Journal of the Mechanics & Physics of Solids, 2011, 59(5): 1094–1114. |
| [7] | Jin L, Takei A, Hutchinson J W. Mechanics of wrinkle/ridge transitions in thin film/substrate systems[J]. Journal of the Mechanics & Physics of Solids, 2015, 81: 22–40. |
| [8] | Wang Z B, Helander M G, Qiu J, et al. Unlocking the full potential of organic light-emitting diodes on flexible plastic[J]. Nature Photonics, 2011, 5(12): 753–757. DOI:10.1038/nphoton.2011.259 |
| [9] | Efimenko K, Rackaitis M, Manias E, et al. Nested self-similar wrinkling patterns in skins[J]. Nature Materials, 2005, 4(4): 293–297. DOI:10.1038/nmat1342 |
| [10] | Kim D H, Ahn J H, Choi W M, et al. Stretchable and foldable silicon integrated circuits[J]. Science, 2008, 320(5875): 507–511. DOI:10.1126/science.1154367 |
| [11] | Coman C D, Bassom A P. The stability of a pre-stressed annular thin film in tension[J]. Journal of the Mechanics & Physics of Solids, 2007, 55(8): 1601–1617. |
| [12] | Klein Y, Efrati E, Sharon E. Shaping of elastic sheets by prescription of non-Euclidean metrics[J]. Science, 2007, 315(5815): 1116–1120. DOI:10.1126/science.1135994 |
| [13] | Sultan E, Boudaoud A. The buckling of a swollen thin gel layer bound to a compliant substrate[J]. Journal of Applied Mechanics, 2007, 75(5): 883–890. |
| [14] | Audoly B, Boudaoud A. Buckling of a stiff film bound to a compliant substrate—Part Ⅰ: Formulation, linear stability of cylindrical patterns, secondary bifurcations[J]. Journal of the Mechanics & Physics of Solids, 2008, 56(7): 2401–2421. |
| [15] | Dervaux J, Amar M B. Localized growth of layered tissues[J]. Ima Journal of Applied Mathematics, 2010, 75(4): 571–580. DOI:10.1093/imamat/hxq023 |
| [16] | Brau F, Damman P, Diamant H, et al. Wrinkle to fold transition: influence of the substrate response[J]. Soft Matter, 2013, 9(34): 8177–8186. DOI:10.1039/c3sm50655j |
| [17] | Zasadzinski J A, Ding J, Warriner H E. The physics and physiology of lung surfactants[J]. Current Opinion in Colloid & Interface Science, 2001, 6(5): 506–513. |
| [18] | Mueggenburg K E, Lin X M, Goldsmith R H, et al. Elastic membranes of close-packed nanoparticle arrays[J]. Nature Materials, 2007, 6(9): 656–60. DOI:10.1038/nmat1965 |
| [19] | Pocivavsek L, Dellsy R, Kern A, et al. Stress and fold localization in thin elastic membranes[J]. Science, 2008, 320(5878): 912–916. DOI:10.1126/science.1154069 |
| [20] | Rivetti M, Neukirch S. The mode branching route to localization of the finite-length floating elastica[J]. Journal of the Mechanics & Physics of Solids, 2014, 69(1): 143–155. |
| [21] | Oshri O, Brau F, Diamant H. Wrinkles and folds in a fluid-supported sheet of finite size[J]. Physical Review E, 2015, 91(5): 052408. DOI:10.1103/PhysRevE.91.052408 |
| [22] | Audoly B. Localized buckling of a floating elastica[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2011, 84(1): 011605. |
| [23] | Piñeirua M, Tanaka N, Roman B, et al. Capillary buckling of a floating annulus[J]. Soft Matter, 2013, 9(46): 10985–10992. DOI:10.1039/c3sm51825f |
| [24] | Huang J, Davidovitch B, Santangelo C D, et al. Smooth cascade of wrinkles at the edge of a floating elastic film[J]. Physical Review Letters, 2010, 105(3): 038302. DOI:10.1103/PhysRevLett.105.038302 |
 2018, Vol. 41
2018, Vol. 41


