近年来,随着深度学习的不断发展,人脸识别技术已经获得了飞跃式的发展[1]。相较于传统的人脸识别技术,如:特征脸、局部特征分析法、基于几何特征法等,深度卷积神经网络(CNNs, convolutional neural networks)进行的人脸识别,能有效的克服诸如光照、多姿态、面部遮挡等干扰。深度卷积神经网络是通过不断的训练从图片中提取特征,克服了手动选择中人为的主观性[2]。对于CNNs的常用人脸识别框架如图 1所述。

|
图 1 人脸识别框架图 Figure 1 Face recognition framework |
早期的人脸识别通过不断的研究网络结构来提升人脸的识别精度,其中较著名的网络有Lenet[3]、Alexnet[4]、Googlenet[4]、VGG[5]、Deep Residual Learning[6]等,其研究结果表现在网络越深,获得的识别精度就越高。然而,这些网络结构需要大量的人脸数据库、较大的计算资源及消耗大量的计算时间,而让许多研究者望而却步,并成为人脸识别的研究瓶颈。为了解决这个问题,文献[7]提出了迁移学习方法,并得到迅速发展,被广大研究者广泛使用。迁移学习可以利用现有的训练好的网络模型,在样本数据不是特别充足的情况下获得较好的结果。但迁移学习的前提是训练数据具有相似性,否则性能将会降低。
由于相似性的训练数据不具有普遍性,而简单的网络结构不能满足需求,因此研究者将目光转向了对数据特征关系的研究。在2005年,文献[8]中就提出可通过计算2幅人脸图像的相似距离来识别人脸,孪生网络[9]被广泛使用,孪生网络能够很好的提取2个输入获取到的特征的相似性。2014年,Taigman等人[10]通过对人脸进行三维对称处理,使用DeepFace孪生网络结构进行训练,该方法在LFW(labeled faces in the wild)人脸数据库上进行测试的精度达到了97.25,接近人眼识别精度。Sun等人[11]在DeepFace的基础上提出了DeepID(deep hidden identity features)网络,采用Softmax损失函数作为监督信号,通过在CelebFaces和WDRef结合的较大的人脸数据库上进行训练,最终在LFW上达到了97.35%的精度。
Softmax损失监督网络在面对未训练过的新标签样本时,由于网络对特征的泛化能力不足,其识别效果不佳。为了解决这个问题,文献[12]中提出使用识别信号和验证信号进行联合监督,其中识别信号能增大不同人脸的差异性,验证信号能减小人脸类内差异,使得在LFW上识别精度达到99.15%。与选取某一层直接使用损失进行分类的方法不同,文献[13]提出了triplet损失函数作为监督信号,直接学习图像到欧式空间上点的映射,2张图像所对应的特征的欧式空间上的点的距离直接对应着2个图像是否相似,来获得更好的分类效果,该方法在LFW上达到了99.63%的精度。
文献[13]中的方法对训练样本数量要求很高,并且计算量增大,训练步骤也变得复杂。为了解决这个问题,研究采用了一种中心损失与Softmax损失进行联合监督的方法,该方法在增大不同人脸间距离的同时,减小同一个人脸内部的距离,从而使学习到的特征具有更好的泛化性和辨别能力,提高深度卷积网络对特征的识别能力。其优点是收敛速度更快、所需样本数量比其他方法少,最后,通过在基准LFW库的实验也证明了算法的有效性,获得了99.31%的人脸识别精度。
1 损失函数及算法步骤在卷积神经网络的前向传播中,通过网络最后一层预测结果与真实结果的比较得到损失,计算误差更新值,通过反向传播对网络的所有权值进行更新。其中,损失层是前向传播的终点,也是反向传播的起点。通过对预测值和真实值的计算,得到损失函数(loss function)的值,而分类中的优化过程实质就是对损失函数进行最小化的过程。可以采用梯度下降法等优化算法计算最小值。
1.1 Softmax损失Softmax函数是Logistic函数[14]的推广,主要用于解决多分类问题。Softmax所获得的结果代表输入图像被分到每一类的概率,若是一个K分类器,则输出是一个K维的向量(向量中元素的和为1)。
对于m个样本,为训练集及其所对应的标签为:{(x(1), y(1)), (x(2), y(2)), …, (x(m), y(m))},其每一个样本的k个估计概率表示如式(1)所示
| $ {\mathit{\boldsymbol{h}}_\theta }({x^{(i)}}) = \left[{\begin{array}{*{20}{c}} {p{\text{ }}({y^{(i)}} = 1|{x^{(i)}};\mathit{\boldsymbol{W}})} \\ {p{\text{ }}({y^{(i)}} = 2|{x^{(i)}};\mathit{\boldsymbol{W}})} \\ \vdots \\ {p{\text{ }}({y^{(i)}} = k|{x^{(i)}};\mathit{\boldsymbol{W}})} \end{array}} \right] = \frac{1}{{\sum\nolimits_{j - 1}^k {{e^{\mathit{\boldsymbol{W}}_j^{\text{T}}x^{\left( i \right)}}}} }}\left[{\begin{array}{*{20}{c}} {{e^{\mathit{\boldsymbol{W}}_1^{\text{T}}x^{\left( i \right)}}}} \\ {{e^{\mathit{\boldsymbol{W}}_2^{\text{T}}x^{\left( i \right)}}}} \\ \vdots \\ {{e^{\mathit{\boldsymbol{W}}_k^{\text{T}}x^{\left( i \right)}}}} \end{array}} \right], $ | (1) |
其中:W1, W2, W3, …, Wk为网络模型参数;k为分类个数;
为了完成网络训练,需要对Softmax的损失函数采用梯度下降法,使其得到的结果达到最小值,其损失函数如公式(2)所示
| $ {L_{\rm{s}}} =- \frac{1}{m}\left[{\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k {1\left\{ {{y^{\left( i \right)}} = j} \right\}\log } } \frac{{{e^{\mathit{\boldsymbol{W}}_j^{\rm{T}}x^{\left( i \right)}}}}}{{\sum\nolimits_{l = 1}^k {{e^{\mathit{\boldsymbol{W}}_l^{\rm{T}}x^{\left( i \right)}}}} }}} \right], $ | (2) |
其中,{y(i)=j}是一个指示性函数,当其值为真时,该函数结果就为1,否则结果就为0。式(2)可简化为
| $ {L_{\rm{s}}} =- \frac{1}{m}\left[{\sum\limits_{i = 1}^m {\log \frac{{{e^{\mathit{\boldsymbol{W}}_{y\left( i \right)}^{\rm{T}}x^{\left( i \right)}}}}}{{\sum\nolimits_{l = 1}^k {{e^{\mathit{\boldsymbol{W}}_l^{\rm{T}}x^{\left( i \right)}}}} }}} } \right]。$ | (3) |
在实际应用中,为了不使任意的(W1, W2, W3, …, Wk)参数为0,通常会在给损失函数加入一权重衰减。损失函数越大,该分类器分类结果为真实标签的概率越小,通过逐次迭代计算损失函数的最小值,得到全局最优解,获得最好性能。
1.2 中心损失文献[15]首次提出中心损失函数,该函数是一种典型的聚类算法。对于一个具有多个特征的CNN来说,在每个批次中可以计算出多个特征中心,计算特征中心的同时计算其损失函数。其损失函数根据该特征值与其对应中心的距离计算得来,因此损失函数可以通过公式(4)、(5)、(6)得出
| $ {L_{\rm{c}}} = \frac{1}{{2m}}\sum\limits_{i = 1}^m {\left\| {{x_i}-{c_{yi}}} \right\|_2^2}, $ | (4) |
| $ \frac{{\partial {L_c}}}{{\partial {x_i}}} = {x_i}-{c_{{y_i}}}, $ | (5) |
| $ \Delta {c_j} = \frac{{\sum\nolimits_{_{i = 1}}^{^m} \delta ({y_i} = j)\cdot({c_j}-{x_i})}}{{1 + \sum\nolimits_{_{i = 1}}^{^m} \delta ({y_i} = j)}}, $ | (6) |
其中:xi表示第i张图片的特征值;cyi则表示该第i张图片所属分类的中心(该分类的特征值的中心);Δcj则表示分类中心的变化。式(5)描述了类内变化情况,其分类的特征中心cyi随着深度特征的变化而变化。式(6)中,当δ(yi=j)取0或者1,也就是当条件yi=j满足时,δ(yi=j)=1,而当条件不满足时,δ(yi=j)=0。
由于训练集较大,在训练过程中要一次性获取所有的中心是不现实,为了获得最优解,文献[15]在每一个小批量中对中心进行分别更新,如式(7)所述。
| $ c_{_j}^{^{t + 1}} = c_{_j}^{^t} + \Delta c_{_j}^{^t}, $ | (7) |
其中,cjt表示的是样本在t时刻的特征中心,在网络训练过程中需要对特征中心不断更新。受到梯度下降中动量[16]概念的启发,为了解决文献[15]中心更新方法完全依赖当前的每一个批量,造成不稳定,在中心更新中引入动量来进行,该方法通过梯度和上一次的权重更新值的线性组合来更新特征中心。其基本思路如图 2所示,首先,按照原来的更新方向更新一步(①线),然后在该位置计算梯度值(②线),然后用这个梯度值修正最终的更新方向(③线)。图 2中描述了2步的更新示意图,其中④线是标准动量更新路径。

|
图 2 特征中心更新方法思路图 Figure 2 Loss joint supervision diagram |
该特征中心更新方法的描述如式(8)所示
| $ \Delta c_{_j}^{^t} = \eta \Delta c_{_j}^{^{t-1}}-\rho \nabla L_{_j}^{^t}(c_{_j}^{^t} + \eta \Delta c_{_j}^{^{t-1}}), $ | (8) |
其中:ρ表示学习率,取值为0-1;∇Ljt则表示cj在批次的梯度;η表示上一次更新的权重,这2个参数需要通过调整来得到最好的结果,一般是根据经验值进行设定的。
至此,经过上述2个步骤的修改,解决了原中心函数在对中心更新时,只考虑了当前批次问题。
1.3 Softmax损失与中心损失联合监督函数通过将Softmax损失与中心损失(center loss)进行联合监督,在增大类间距离的同时,减小类内距离,使其获得的特征具有更强的识别能力,如式(9)所示
| $ L = {L_S} + \lambda {L_C} =- \frac{1}{m}\left[{\sum\limits_{i = 1}^m {\log \frac{{{e^{\mathit{\boldsymbol{W}}_{y\left( i \right)}^{\rm{T}}{x^{\left( i \right)}}}}}}{{\sum\nolimits_{l = 1}^k {{e^{\mathit{\boldsymbol{W}}_l^{\rm{T}}{x^{\left( i \right)}}}}} }}} } \right] + \frac{\lambda }{2}\sum\limits_{i = 1}^m {\left\| {{x_i} -{c_{yi}}} \right\|_2^2}, $ | (9) |
式中:λ用来平衡2个损失,合适的λ选择有助于网络特征识别能力的增强;cyi是yi类的样本中心,其中,当λ=0时,可以将该函数认为是仅有Softmax损失的情况。
通过联合监督方法不仅解决了对比损失中无法采集合适的样本对的问题,同时也解决了三重损失中复杂采样的问题。在该中心损失中,采用了对比损失中同类样本损失公式,用同类样本中的类中心替换了其中的一个同类样本,而异类时,是直接采用Softmax损失进行计算。
1.4 网络参数配置及算法步骤为了有效的实现非限制条件下的人脸识别,将Softmax损失与中心损失相结合,其联合损失的监督示意图如图 3所示,对于整个训练网络的具体参数的配置见实验部分。
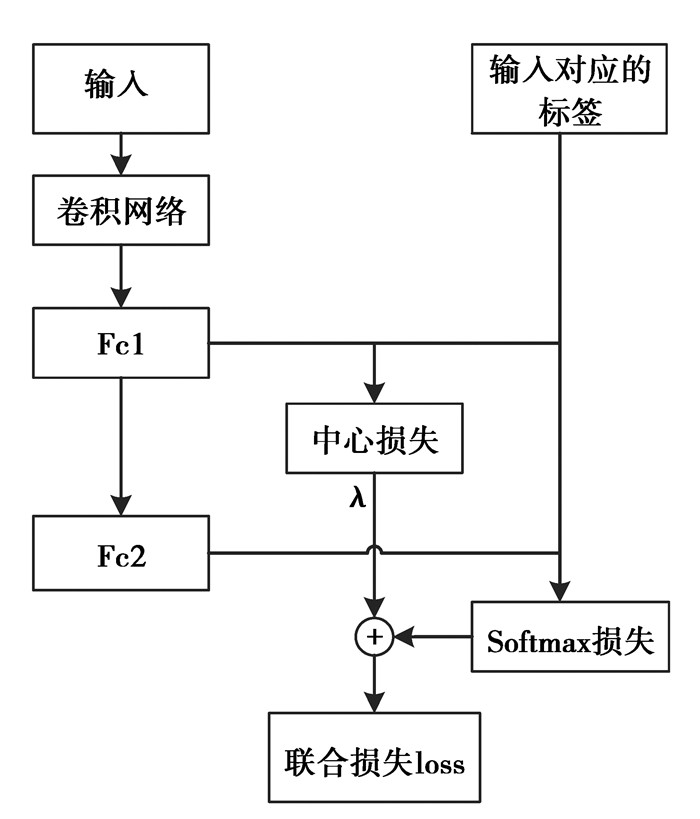
|
图 3 损失联合监督示意图 Figure 3 Loss joint supervision diagram |
通过对网络结构的研究,构建网络,对于联合监督算法部分,将算法的输入抽象为:训练数据集{xi},分别初始化池化层和loss层的参数θc、W及{cj|j=1, 2, …, n},同时输入参数:λ、α和学习率μt,其中迭代的次数t初始化为0。输出则抽象为输出参数θc,因此归纳联合监督的人脸识别算法步骤如下所示。
步骤1:判断是否收敛,不收敛则执行步骤2;
步骤2:迭代次数t自增,即t←t+1;
步骤3:计算联合损失Lt:Lt=LSt+LCt
步骤4:计算反向传播误差
步骤5:更新参数W:通过公式
步骤6:更新参数cj,通过Δcjt=ηΔcjt-1-ρ∇Ljt(cjt+ηΔcjt-1)公式进行详细计算;
步骤7:更新参数θc,通过公式
步骤8:判断是否收敛,若收敛则迭代结束,否则,从步骤1开始重复执行。
2 实验及结果分析为验证算法的有效性,选用人脸基准库LFW人脸库进行人脸识别实验。实验选用网络中单独使用Softmax损失监督的Model A、Softmax损失与对比损失联合监督的Model B几个使用最广泛的网络模型与算法的Model C进行对比分析。
2.1 网络模型及数据集 2.1.1 网络模型VGGNet[17]是Andrew Zisserman教授研究团队(Oxford)提出的一种CNN,该网络相较于AlexNet具有更深的网络结构,通常有16~19层,且其所有卷积层都使用了同样的大小的卷积核,大小为3×3。VGGNet在2014年的ILSVRC定位和分类2个问题上分别取得了第一名和第二名。因此,全部采用3×3的网络结构来组建网络。此外,受Resnet[18]的启发,在VGGNet基础上添加残差网络结构,其网络结构如图 4所示。其卷积层由一个3×3的步长为1的卷积网络和一个PReLU激活函数组成。对于图 4中的LC层,其结构如图 5所示。其中,特征图大小分别为128,256,521,2个全连接层的输出维度都为512。
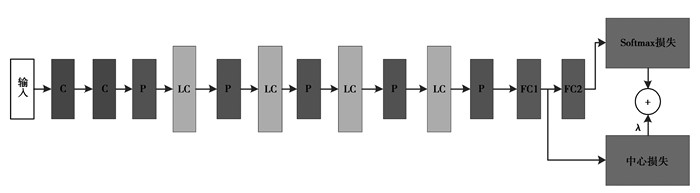
|
图 4 网络结构模型图 Figure 4 Network model |

|
图 5 LC层结构框图 Figure 5 Structure diagram of LC |
① 训练数据集
选取CASIA-WebFace作为训练数据集,其包含10 575人的约500 K张图片。由于该数据库与LFW有3个人脸是重复的,选取了10 572个人的人脸图像,对其进行剪切、对齐处理(图像剪切为112×96),采用4:1的比例拆分训练数据和验证数据。在训练过程中,对训练和验证数据做镜像处理。其训练数据和验证数据如图 6所示。

|
图 6 训练及验证数据集 Figure 6 Data sets of Training and validation |
② 测试数据集
选取目前广泛使用的LFW标准人脸识别数据集,该数据集是是专门用来研究人脸识别问题的数据集。该数据集包含5 749人,共13 233张人脸图像。LFW定义了3个标准的协议(无监督、限制与非限制)去评估人脸识别的性能。这里选取了6 000组测试比对集,其中3 000组为相同人的比对集,3 000组为不同人的比对集。经过对人脸进行矫正和剪切的预处理后[19-20],其人脸如图 7所示,其中绿色方框中的人脸表示2组中的人脸是同一个人,红色方框中的人脸表示2组中的人脸不是同一个人。

|
图 7 测试数据集 Figure 7 The test data set |
研究所提算法中,通过使用ρ来控制中心的学习率,λ用来平衡Softmax及中心2个损失,从而加强网络对特征的识别能力。η则用来校正特征中心的更新,因此这3个参数对所述算法起着至关重要的作用,下面分别对其进行讨论。
1) 参数λ对人脸识别精度的影响
本实验,通过固定ρ及动量η,改变λ参数的方式进行试验,从参考文献[15]中知道,当ρ=0.5的时候,能够获得较高的中心学习率。因此,第一个试验,固定ρ=0.5,η=0.5,而使λ从0变化到1,从而学习到不同的网络模型。
在LFW数据集上的测试结果如图 8所示,由图可知,所提Softmax损失及中心损失联合监督算法的优越性,其人脸识别测试精度,要高于仅Softmax损失监督下(当λ=0时,训练网络仅有Softmax损失监督)的测试精度。同时,从图 8中也可以得到,一个合适的λ值有助于提高人脸识别精度,参数λ的最佳结果为0.003。

|
图 8 基于LFW数据集上的人脸识别精度(α=0.5, η=0.5) Figure 8 Face recognition accuracy based on LFW data set |
2) 学习率ρ对人脸识别精度的影响
根据本章实验(1)中获得的最优结果,本节实验固定λ=0.003,η=0.5,而让ρ从0.01变化到1,从而学习到不同的模型。
分别采用这些模型在精准库LFW上做人脸识别测试,可以得到该实验的人脸识别精度如图 9所示。由图 9分析得出,选择合适的ρ值,同样有助于提高训练网络的人脸识别精度。根据实验分析,参数ρ的最佳结果为0.6。
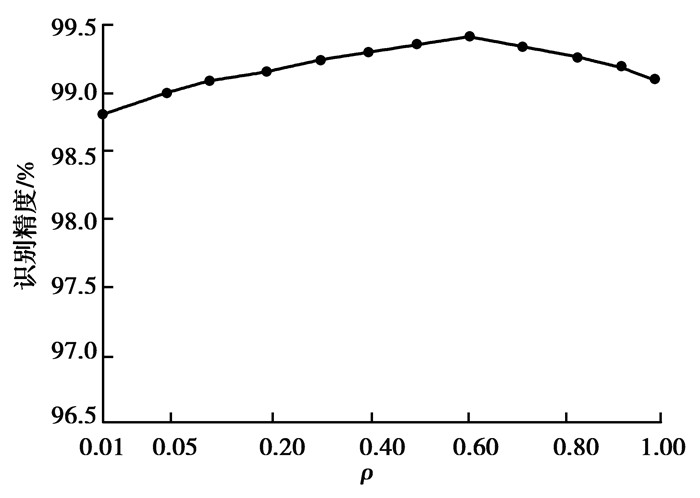
|
图 9 LFW数据集上的人脸识别精度(λ=0.003, η=0.5) Figure 9 Face recognition accuracy on LFW data set |
3) 参数η对人脸识别精度的影响
根据实验(1)、(2)获得的最优结果,本节实验通过固定ρ=0.6,λ=0.003,而让参数η在0到1之间η发生变化,从而训练到不同的网络模型。通过LFW数据集上的测试,得到该实验的人脸识别精度,其实验结果如图 10所示。

|
图 10 LFW数据集上的人脸识别精度(λ=0.003, ρ=0.6) Figure 10 Face recognition accuracy on LFW data set |
由图 10分析得出,一个合适的动量选择,能够提高训练网络的人脸识别精度,从实验结果来看,当η取0.9时,人脸识别精度最高。同时,将其与图 9、图 10对比发现,最佳的λ、ρ及η值,能够在总体上提高人脸识别精度。
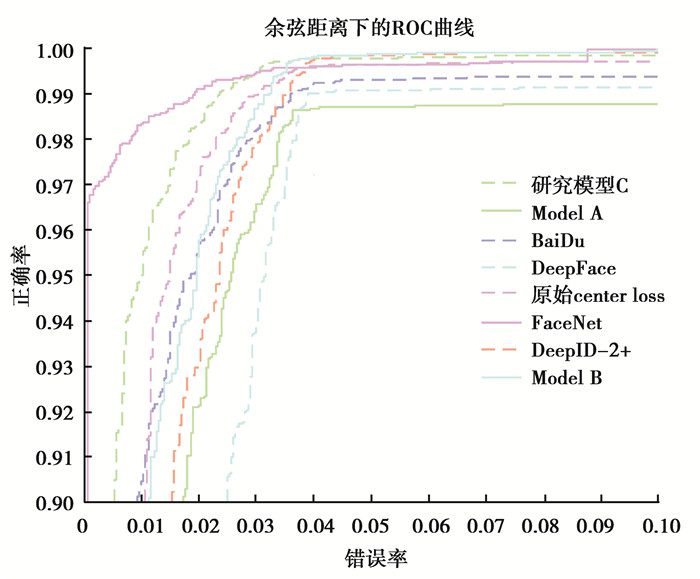
2.3 不同网络模型下的人脸识别精度比较ROC(receiver operating characteristic)曲线和AUC(area under curve)常被用来评价一个二值分类器(binary classifier)的优劣[21]。其中,AUC被定义为ROC曲线下的面积。为了说明所提联合监督算法在人脸识别精度中的优势,将其与目前获得了最高人脸识别精度的几种经典网络模型比较分析,其中,网络模型是在CAISA-webface数据集上训练而来的,该数据集中的任何一张人脸都与LFW上的人脸不同,并且所采用的参数ρ=0.6,λ=0.003,η=0.9。
在实验中,通过人脸验证试验绘制ROC曲线,从而评价算法训练下的分类特征的好坏。人脸验证试验是:对于LFW中给定的6 000组测试人脸,分别判断他们是否是同一个人。经过试验,在LFW测试集中达到了99.31%的平均精度,与表 1中所列方法的平均精度和ROC曲线的比较分别如表 1和图 11所示,其中用Model A表示仅使用Softmax损失函数监视的模型,Model B表示Softmax损失和对比损失联合监视的模型,而Model C则表示所提模型。
| 表 1 不同模型下的人脸识别性能比较 Table 1 Recognition of face recognition performance under different models |
|
图 11 LFW数据集上人脸识别的ROC曲线 Figure 11 ROC of face verification on LFW |
从表 1及图 11的实验数据分析来看,所提算法(Softmax损失与center损失联合监督)比单一的损失监督Model A,在相同训练数据图片的情况下获得了较高的识别精度,在LFW基准库上识别精度从97.35%提高到99.31%。该对比结果可以证明,联合监督方法相比单一监督方法,在对特征的分类能力上有显著的提升。其次,研究还将算法与当前使用最为广泛的联合监督Model B进行比较,从实验结果来看,表 1显示Model C的人脸识别精度从原来的99.28%提高到99.31%,表 2可见其训练时间已经缩短。实验表明网络收敛速度已经加快,在减小类内距离上有更加显著的优势。最后,表 1还列出了当前表现最好的几种经典模型,结合图 11的ROC曲线。可见所提算法模型的识别结果,能够在使用较小训练数据集的情况下,获得较高的人脸识别精度。
| 表 2 不同center loss下的人脸识别性能比较 Table 2 The performance of face recognize under different center loss |
笔者提出了一种基于中心损失与Softmax损失联合监督的人脸识别算法,在LFW人脸库上的实验结果表明:算法能够提高网络对特征的识别能力,将中心损失与Softmax损失相结合,克服了Softmax损失在面对未训练过的新标签样本时,泛化能力不足的问题。同时,重点引入动量的概念,在分类中心更新的时候,通过保留之前的更新方向,同时利用当前批次的梯度微调最终的更新方向,该方法可以在一定程度上增加稳定性,提高网络的学习效率。
最后,实验表明:在较小的网络训练集的基础上,算法获得了99.31%的人脸识别精度,从而验证了算法在提高网络对特征的识别能力上的优越性。
| [1] | Parkhi O M, Vedaldi A, Zisserman A, et al. Deep face recognition[C]//British Machine Vision Conference. Swansea, UK: British Machine Vision Association, 2015: 41-42. |
| [2] | Mufti H N, Abidi S, Abidi S R, et al. Predictors of post-operative delirium in cardiac surgery patients; a machine learning approach[J]. Canadian Journal of Cardiology, 2014, 30(10): 237–238. |
| [3] | LeCun L, Bottou Y, Bengio P, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278–2323. DOI:10.1109/5.726791 |
| [4] | Ballester P, Araujo R M. On the performance of GoogLeNet and alexNet applied to sketches[C]//Thirtieth AAAI Conference on Artificial Intelligence. Phoenix, USA: AAAI Press, 2016: 1124-1128. http://dl.acm.org/citation.cfm?id=3015979 |
| [5] | Day M J, Horzinek M C, Schultz R D, et al. Guidelines for the vaccination of dogs and cats[J]. Journal of Small Animal Practice, 2007, 48(9): 528. DOI:10.1111/jsap.2007.48.issue-9 |
| [6] | He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[G]//Computer Vision and Pattern Recognition, Las Vegas, USA: IEEE, 2015: 770-778. |
| [7] | Sinno J, Yang Q. A survey on transfer learning[J]. IEEE Transactions on Knowledge & Data Engineering, 2010, 22(10): 1345–1359. |
| [8] | Hadsell R, Chopra S, Lecun Y, et al. Dimensionality reduction by learning an invariant mapping[C]//Computer Vision and Pattern Recognition, Conference on 2006 IEEE Computer Society. New York: IEEE, 2006: 1735-1742. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1640964 |
| [9] | Chopra S, Hadsell R, Lecun Y, et al. Learning a similarity metric discriminatively, with application to face verification[C]//Computer Vision and Pattern Recognition, 2005. New York: IEEE, 2005: 539-546. https://dl.acm.org/citation.cfm?id=1068961 |
| [10] | Taigman Y, Yang M. Deepface: closing the gap to human-level performance in face verification[C]//Computer Vision and Pattern Recognition. Columbus, USA: IEEE, 2014: 1701-1708. https://www.cv-foundation.org/openaccess/content_cvpr_2014/papers/Taigman_DeepFace_Closing_the_2014_CVPR_paper.pdf |
| [11] | Sun Y, Wang X, Tang X. Deep learning face representation from predicting 10, 000 classes[C]//IEEE Conference on Computer Vision and Pattern Recognition. Columbus, USA: IEEE Computer Society, 2014: 1891-1898. http://doi.ieeecomputersociety.org/10.1109/CVPR.2014.244 |
| [12] | Sun Y, Wang X, Tang X, et al. Deep learning face representation by joint identification-verification[C]//NIPS Montred, CANADA: MIT Press, 2014, 27: 1988-1996. https://dl.acm.org/citation.cfm?doid=1553374.1553469 |
| [13] | Cheng D, Gong Y, Zhou S, et al. Person reidentification by multi-channel parts-based CNN with improved triplet loss function[C]//Computer Vision and Pattern Recognition. Las Vega S, USA: IEEE, 2016: 1335-1344. |
| [14] | King G, Zeng L. Logistic regression in rare events data[J]. Political Analysis, 2001, 9(2): 137–163. DOI:10.1093/oxfordjournals.pan.a004868 |
| [15] | Wen Y, Zhang K, Li Z, et al. A discriminative feature learning approach for deep face recognition[C]//Computer Vision-ECCV 2016. Amsterdam: Springer International Publishing, 2016: 11-26. |
| [16] | Qian N. On the momentum term in gradient descent learning algorithms[J]. Neural Networks the Official Journal of the International Neural Network Society, 1999, 12(1): 145–151. DOI:10.1016/S0893-6080(98)00116-6 |
| [17] | Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[J]. Computer Science, 2014, 6(1): 1409–1556. |
| [18] | Szegedy C, Ioffe S, Vanhoucke V, et al. Inception-v4, Inception-ResNet and the impact of residual connections on learning[C]//AAAI. Palo Alto, California: AAAI, 2017: 4278-4284. http://arxiv.org/abs/1602.07261 |
| [19] | Kazemi V, Sullivan J. One millisecond face alignment with an ensemble of regression trees[C]//Computer Vision and Pattern Recognition. Columbus, USA: IEEE, 2014: 1867-1874. |
| [20] | Klawonn F, H ppner F, May S. An alternative to ROC and AUC analysis of classifiers[C]//International Conference on Advances in Intelligent Data Analysis X. Berlin: Springer, 2011: 210-221. |
 2018, Vol. 41
2018, Vol. 41


