现代加工中,高速切削因其加工效率高、加工工件质量高、加工成本低的特点已逐渐成为切削加工主流,但高速切削中,刀具会承受高温、高压、高频冲击,对其切削性能及可靠性要求较高。同时随着数控机床以及智能车间的发展,刀具种类及数量均与日俱增,对刀具的管理提出了更高要求。如果刀具磨损或破损不能及时发现,会严重影响加工质量及机床寿命。统计表明,刀具失效导致的换刀时间占整个停机时间的20%[1]。因此,刀具是切削加工中保证加工质量,提高生产效率的一个重要因素[2],刀具磨损监测对加工制造的成本、质量以及管理决策有重要意义。
刀具磨损监测主要包括直接法和间接法。直接法有放射线法、电阻测量法等,该类方法直接测量刀具质量和形状等变化,检测精度高,但大多需要停机操作,只能作为离线测量方式。间接法主要分析与刀具磨损相关的参量变化[3-4],如切削力、切削温度、振动等,从而完成监测,对切削加工过程影响较小,适用于在线监测。目前基于间接法的刀具磨损量识别广泛采用机器学习算法,如神经网络[5]、隐式马尔科夫模型[6-7]和支持向量机[8-9]等,利用其黑箱处理方式,忽略复杂的加工过程,建立被监测参量与刀具磨损的映射关系[10]。
使用此类方法存在的主要问题在于为获取足够的训练样本,需进行大量切削实验;切削过程中的信号处理结果也将直接关系预测结果的准确性;局部最优解和泛化能力的局限性会影响磨损监测的稳定性;收敛速度以及模型结构将决定计算成本以及在线监测的可能性。针对上述问题,笔者采用单隐层前馈神经网络的极限学习机(extreme learning machine, ELM)[11]建立刀具磨损监测模型,提出一种改进的人工蜂群算法(improved artificial bee colony, IABC)优化其随机产生的输入层权值和隐含层阈值,提高预测结果稳定性,并在范例分析中对铣刀连续加工过程中的力信号、振动信号以及声发射信号进行分析,提取敏感特征作为监测模型的输入,验证结果表明了该模型的有效性。
1 刀具磨损监测模型的建立 1.1 刀具磨损分析在金属切削加工中,刀具磨损过程主要分为初期磨损、正常磨损以及急剧磨损3个阶段,急剧磨损阶段时,持续上升的刀具温度将导致加工工件的状态急剧恶化,此时刀具磨损曲线呈指数形式,同时因为在刀具正常磨损与急剧磨损之间没有明显的过渡,使得很难避开该阶段[12]。切削加工中刀具前刀面和后刀面都会发生磨损,但是一般认为相较于前刀面磨损,后刀面磨损对加工精度和刀具寿命[13]影响更大,图 1为光学显微镜下的车刀后刀面磨损情况,整个磨损带较为均匀但在靠近工件外表皮附近出现明显凹痕的边界磨损区。磨钝后的刀具加工工件时会产生刮痕、剧烈震动等情况,严重影响加工质量,如图 2所示为刀具磨钝前后加工工件表面对比图。

|
图 1 后刀面磨损情况 Figure 1 Flank wear of the cutting tool |

|
图 2 工件表面对比图 Figure 2 Comparison of machinedpart surface by worn tool and normal tool |
人工蜂群算法是一种广义的领域搜索算法,借助启发式搜索策略,每次迭代都进行了全局和局部搜索,极大程度地避免局部最优解[14-15],但基本蜂群算法存在开采能力差,收敛速度低的缺点[16]。针对此,笔者提出引入一只虚拟蜂,该虚拟蜂通过在当前最优解各维添加扰动变量,寻找新的食物源,从而提高算法的开发能力和收敛速度。虚拟蜂定义式为
| $ {{\mathit{V}}_{\mathit{j}}}\text{=}{{\mathit{y}}_{\mathit{j}}}\text{+}\mathit{\varepsilon }\text{ }\!\!\cdot\!\!\text{ }\left( \mathit{r}\text{-0}\text{.5} \right)\text{, }\mathit{j}\text{=1, 2, }\cdots \text{, }\mathit{D}\text{, } $ | (1) |
式中:yj为当前最优解的第j维;ε为扰动系数;r为[0, 1]的随机数。
式(1)中的随机参数使得虚拟蜂能够搜索全局最优解的邻域,ε可调节虚拟蜂探索开发能力,当ε取较小值时,虚拟蜂搜索全局最优解附近相对较小的区域,从而有较好的开发能力;当ε增加时,虚拟蜂的探索能力增强,ε为自适应系数,定义如下:
| $ \mathit{\varepsilon }\text{=}\frac{\text{0}\text{.1*}\mathit{m}}{\mathit{M}}\text{ }\!\!\cdot\!\!\text{ }{{\mathit{y}}_{\mathit{j}}}\text{, } $ | (2) |
式中:m为当前循环次数;M为最大循环次数。
在循环开始阶段ε有较小值,保证较好的开发能力,随着循环次数增加,ε值逐渐增大,从而改善搜索能力,避免陷入局部最小值。为了确保能持续得到更优解,虚拟蜂每一维新生成时都会根据适应度与其原位置进行贪婪选择。此外为了尽可能利用当前最优信息,虚拟蜂在雇佣蜂阶段和观察蜂阶段和其他普通蜜蜂一样寻找食物源, 但为了保持整个蜂群的多样性,虚拟蜂不允许雇佣和影响其他蜜蜂。
1.3 改进人工蜂群算法优化的极限学习机 1.3.1 食物源设计每个食物源为一组输入层权值和隐含层权值的组合,其表示如下:
| $ \begin{align} &{{\mathit{\boldsymbol{x}}}_{\mathit{i}}}\text{= }\!\![\!\!\text{ }{{\mathit{w}}_{\text{1, 1}}}\text{, }{{\mathit{w}}_{\text{1, 2}}}\text{, }\cdots \text{, }{{\mathit{w}}_{\text{1, }\mathit{n}}}\text{, }\cdots \text{, }{{\mathit{w}}_{\mathit{c}\text{, }\mathit{d}}}\text{, }\cdots \text{, }{{\text{w}}_{\mathit{L}\text{, 1}}}\text{, }{{\mathit{w}}_{\mathit{L}\text{, 2}}}\text{, }\cdots \text{, }{{\mathit{w}}_{\mathit{L}\text{, }\mathit{n}}}\text{, }{{\mathit{b}}_{\text{1}}}\text{, }{{\mathit{b}}_{\text{2}}}\text{, }\cdots \text{, }{{\mathit{b}}_{\mathit{c}}}\text{, }\cdots \\ &\text{, }{{\mathit{b}}_{\mathit{L}}}{{\text{ }\!\!]\!\!\text{ }}^{\text{T}}}\text{, }\mathit{i}\text{=1, 2, }\cdots \text{, }\mathit{N}\text{。} \\ \end{align} $ | (3) |
式中:wc, d为连接第c个隐含层节点和第d个输入层节点的权值;bc为第c个隐含层节点阈值;wc, d和bc均取[-1, 1]的实数;n和L分别为输入层和隐含层节点数。
1.3.2 适应度设计为反应预测结果的准确性和精确性,采用均方根误差:
| $ \mathit{R}\text{=}\sqrt{\frac{\sum\limits_{\mathit{e}\text{=1}}^{\mathit{E}}{{{\text{(}{{\mathit{y}}_{\mathit{e}}}\text{-}{{{\mathit{{y}'}}}_{\mathit{e}}}\text{)}}^{\text{2}}}}}{\mathit{E}}}\text{, } $ | (4) |
式中:y′e为刀具磨损实际值;ye为刀具磨损预测值;E为样本数。
均方根误差较小的解应该对应较大的适应度,因此取均方根误差的倒数作为适应度值:
| $ \mathit{F}\text{=}\frac{\text{1}}{\mathit{R}}。$ | (5) |
设置种群大小N,最大循环次数M,控制参数S。整个IABC-ELM的步骤如下。
步骤1 训练阶段。
1a:随机产生N个食物源。
1b:解码每个食物源获得ELM输入权值和偏置,根据训练样本,计算对应输出权值,得到ELM模型,从而算出刀具磨损量预测值。
1c:根据式(4)和式(5)计算刀具食物源的适应度,选择适应度较大的前N/2个食物源对应的蜂群作为雇佣蜂。
1d:设置当前循环次数m=1。
步骤2 当m≤M时执行以下步骤。
2a:选择当前最优解,根据式(1)和式(2)产生虚拟蜂。
2b:雇佣蜂阶段。
2b1:雇佣蜂和虚拟蜂在之前的食物源附近寻找新的食物源。
2b2:重复步骤1b和1c,评价新的食物源并通过比较从新旧食物源中选择优质食物源。
2c:计算每只雇佣蜂的被选择概率。
2d:观察蜂阶段。
2d1:观察蜂选择雇佣蜂跟随。
2d2:观察蜂和虚拟蜂在之前的食物源附近寻找新的食物源。
2d3:重复步骤1b和1c,评价新的食物源并通过比较从新旧食物源中选择优质食物源。
2e:侦察蜂阶段。如果S次循环后某一食物源附近仍未有更好的解被发现,则其雇佣蜂变为侦察蜂并重新寻找食物源。
2f:记录整个蜂群(包括虚拟蜂)的当前最优解并更新循环次数m=m+1。
步骤3 测试阶段。
3a:输出并解码获得的最优解,得到ELM的最优输入权值和偏置。
3b:计算ELM的输出权值,根据测试数据集计算刀具的磨损预测值。
步骤1a中的初始食物源和步骤2e的新食物源由式(6)产生:
| $ {{\mathit{x}}_{\mathit{i}\text{, }\mathit{j}}}\text{=}\mathit{x}_{\mathit{j}}^{\text{min}}\text{+}\mathit{r}\text{ }\!\!\cdot\!\!\text{ (}\mathit{x}_{\mathit{j}}^{\text{max}}\text{-}\mathit{x}_{\mathit{j}}^{\text{min}}\text{), }\mathit{i}\text{=1, 2, }\cdots \text{, }\mathit{N}\text{, }\mathit{j}\text{=1, 2, }\cdots \text{, }\mathit{D}\text{, } $ | (6) |
式中:xjmax和xjmin分别表示第j维变量上下界;r为[-1, 1]的随机数;D为根据式(3)生成的食物源长度。
步骤2b1和步骤2d2中新的食物源由式(7)产生:
| $ {{\mathit{v}}_{\mathit{i}\text{, }\mathit{j}}}\text{=}{{\mathit{x}}_{\mathit{i}\text{, }\mathit{j}}}\text{+}{{\mathit{\varphi }}_{\mathit{i}\text{, }\mathit{j}}}\text{(}{{\mathit{x}}_{\mathit{i}\text{, }\mathit{j}}}\text{-}{{\mathit{x}}_{\mathit{q}\text{, }\mathit{j}}}\text{), }\mathit{q}\in \text{ }\!\!\{\!\!\text{ 1, 2, }\cdots \text{, }\mathit{N}\text{/2 }\!\!\}\!\!\text{ }\!\!\And\!\!\text{ }\mathit{j}\in \text{ }\!\!\{\!\!\text{ 1, 2, }\cdots \text{, }\mathit{D}\text{ }\!\!\}\!\!\text{ , } $ | (7) |
式中:q和j随机选取并且q不等于i;φi, j为[-1, 1]之间的随机数。
步骤2c中雇佣蜂的被选择概率由式(8)确定:
| $ {\mathit{P}_\mathit{i}}{\rm{ = }}\frac{{{\mathit{F}_\mathit{i}}}}{{\sum\limits_{\mathit{i}{\rm{ = 1}}}^{\mathit{N}{\rm{/2}}} {{\mathit{F}_\mathit{i}}} }}{\rm{, }} $ | (8) |
式中Fi表示第i个解的适应度。
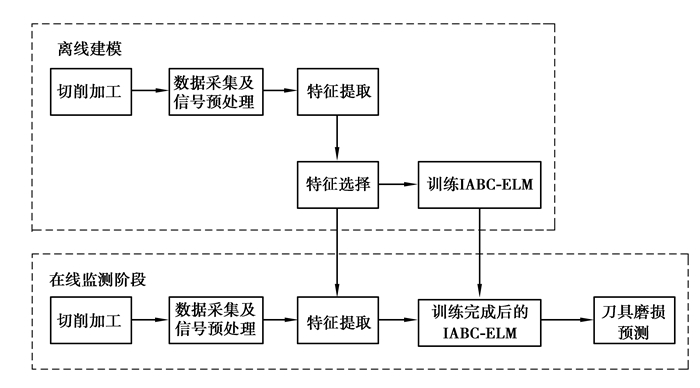
基于该模型的刀具磨损监测流程可概括如图 3所示。
|
图 3 刀具磨损在线监测流程 Figure 3 Procedure of online tool wearmonitoring |
实验数据来自PHM Society(2010)公开的刀具磨损数据集[17],实验在Röders Tech RFM760数控机床上进行,加工刀具为三刃球头铣刀,加工材料为不锈钢(HRC 52)。机床的工作台与工件间安装Kistler压电石英三向平台测力仪,测量X、Y、Z 3个方向力信号(X轴为走刀方向,Y轴为径向切深方向,Z轴为轴向切深方向);工件上安装3个压电式加速度传感器和Kistler声发射传感器分别测量X、Y、Z 3个方向的振动信号和声发射信号。监测信号通过相应处理(如电荷放大或耦合)后经A/D转换后进入PC机,数据采集卡为NI DAQ PCI1200,采样频率为50 kHz。设置机床切削参数如表 1所示, 铣削方式为端铣,每次走刀108 mm,走刀后测量3个切削刃的后刀面磨损值,共走刀315次。
| 表 1 切削用量设置 Table 1 Parameters of milling process |
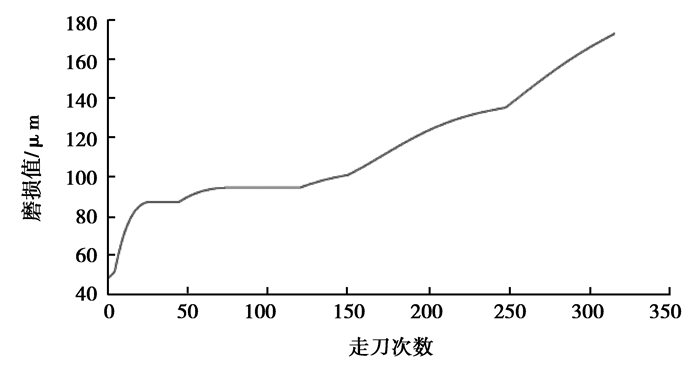
实验中每次采样点个数不同,为了方便数据处理,选取每次采样的前4 000点数据作为原始数据,以3个切削刃后刀面中的最大磨损值作为整个刀具的磨损值,如图 4所示。
|
图 4 刀具磨损曲线 Figure 4 Curve of tool wear |
经传感器采集到的信号为非平稳信号且含有噪声杂质,难以用来直接分析,需对其进行信号处理,提取表征刀具磨损的特征向量,为后面的刀具磨损预测模型做准备。笔者对各传感器信号进行时域分析,提取信号均值、均方根值、方根幅值、偏斜度及峰峰值5种时域特征,共得到35个样本时域特征。采用皮尔逊相关系数法对得到的信号时域特征和刀具磨损值进行相关分析,选取能够准确反映刀具磨损的特征。相关系数计算公式为
| $ R\left( {X,Y} \right){\rm{ = }}\frac{{\sum {\left( {X{\rm{ - }}\bar X} \right)\left( {Y{\rm{ - }}\bar Y} \right)} }}{{\sqrt {\sum {{{\left( {X{\rm{ - }}\bar X} \right)}^{\rm{2}}}} \sum {{{\left( {Y{\rm{ - }}\bar Y} \right)}^{\rm{2}}}} } }}, $ | (9) |
式中:X为特征值;Y为刀具磨损量。
相关系数越大,则该特征与刀具磨损量之间的相关度越高,这里选择相关度较大的5个特征:X方向力信号方根幅值,Y方向力信号峰峰值,Z方向力信号峰峰值,X方向振动信号方根幅值,Z方向振动信号方根幅值。
切削加工中,刀具和工件间会释放大量能量,这些能量主要体现在切削热、切削力、振动和声发射上,本次实验所用传感器能获取后三者的信息,因此可以对刀具磨损过程中的内禀模态能量比进行特征提取。
采用EMD方法对原始信号进行分解,获得一系列代表信号本质的IMF分量。这些IMF分量数量较多,并且由于原始信号中除了刀具磨损信息以外还混杂有机床状态、外界噪声等干扰成分,所以IMF分量中含有虚假成分。因此对原始信号和各分量进行相关性分析,保留相关性较大的敏感分量,剔除虚假分量后的IMF分量中含有原信号中的主要信息[9],计算选取的IMF分量的归一化能量作为特征值。其计算步骤如下。
1) 求各传感器信号的敏感IMF的能量和总能量:
| $ \mathit{E}_\mathit{v}^\mathit{u}{\rm{ = }}\sum\limits_{\mathit{t}{\rm{ = 1}}}^\mathit{P} {{{\left| {\mathit{c}_\mathit{v}^\mathit{u}\left( \mathit{t} \right)} \right|}^{\rm{2}}}} {\rm{, }}\left( {\mathit{u}{\rm{ = 1, 2, }} \cdots {\rm{, 7;}}\mathit{t}{\rm{ = 1, 2, }} \cdots {\rm{, }}P} \right){\rm{, }} $ | (10) |
式中:cvu为第u个传感器信号的第v个敏感IMF; P为数据点个数,记
2) 计算各传感器的敏感IMF能量与总能量之比作为特征值:
| $ \mathit{x}_\mathit{v}^\mathit{u}{\rm{ = }}\frac{{\mathit{E}_\mathit{v}^\mathit{u}}}{{{\mathit{E}^\mathit{u}}}}。$ | (11) |
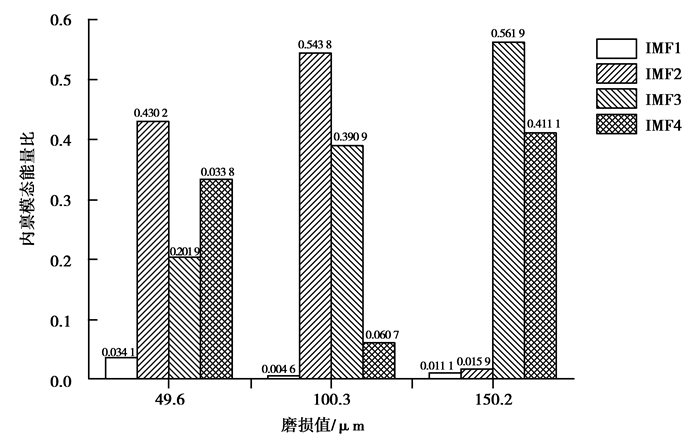
图 5表示后刀面磨损值分别为49.6,100.3,150.2 μm时,X方向力信号敏感IMF分量能量比。
|
图 5 3种状态下的X方向力信号能量比 Figure 5 Energy ratio of X-direction force on three conditions |
可以看出随着刀具磨损的加剧,各IMF分量的能量比发生明显变化。对得到的各信号的IMF分量的能量比与刀具磨损值进行相关性分析,选取相关性系数较大的Z方向力信号的IMF3、IMF4分量能量比。
2.3 预测结果及模型比较315组样本数据中随机选取15组作为测试集,剩余300组作为训练集,进行特征提取和筛选,输入监测特征向量和输出刀具磨损值之前分别对其进行归一化和反归一化处理。同时为了更好评价模型泛化性能以及优化隐含层节点数目[18],采用10折交叉验证法对模型进行训练:将训练集随机均分为10份,轮流取其中1份作为验证集,其余9份用于训练模型,取10次验证误差的均值作为模型评价标准,确定最优隐含层节点数目。本次实验IABC-ELM模型参数最终设置如下:N=10,S=30, M=150,隐含层节点数为10。为避免每次仿真参数随机初始化的影响,记录运行10次的平均输出值为最终预测值,预测结果如表 2所示。
| 表 2 测试样本刀具磨损量预测值及误差 Table 2 Prediction results of proposed model |
可以看出IABC-ELM对大部分测试数据有较好的预测结果,只有一处较大的预测误差,即12.961 8%,由图 4可看出该处对应初期磨损阶段刀具磨损波动较大。为进一步验证模型性能,用相同数据集对BP神经网络、ELM、ABC-ELM进行训练。BP神经网络采用7-9-1结构,ABC与IABC参数设置相同,ELM和ABC-ELM的隐含层节点数同样由10折交叉验证确定,表 3为各模型性能比较,各结果均为10次测试误差累计值的平均值。
| 表 3 不同模型性能比较 Table 3 Performances of different models |
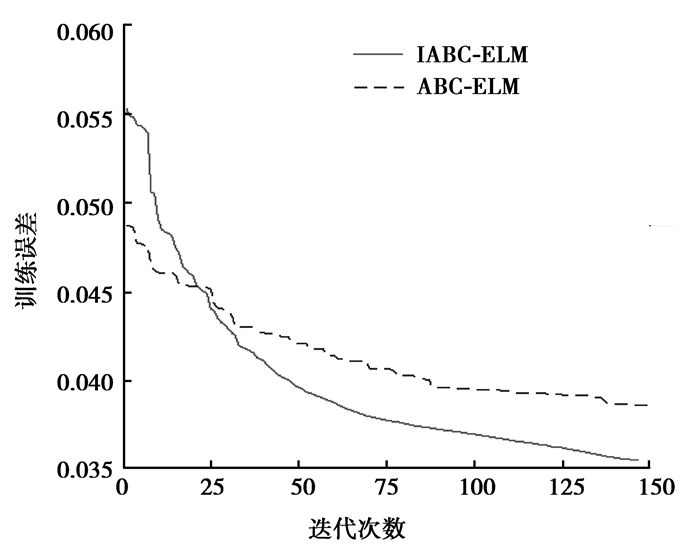
可以看出BP神经网络的预测效果较差,可能是因为陷入局部最优。输入层权值和隐含层阈值经过优化的ABC-ELM和IABC-ELM预测精度更高并且隐含层节点数相对于ELM明显减小,简单的网络结构保证了更好的泛化性能以及预测时的计算成本,这对于实现刀具磨损实时监测尤为重要。另外,IABC-ELM的测试集平均准确率达到97%以上,能够满足实际生产中的刀具磨损监测需求。图 6所示为一次训练中ABC-ELM和IABC-ELM的训练误差变化曲线,可见在训练过程中ABC-ELM多次陷入局部最优,而IABC-ELM由于虚拟蜂的存在,极大程度避免了局部最优,训练误差持续减小,且收敛速度明显加快。
|
图 6 IABC-ELM和ABC-ELM训练过程比较 Figure 6 Training process comparison of IABC and ABC |
笔者对高速铣削中的力信号、振动信号和声信号进行分析,通过时域分析、EMD和相关性分析等方法对信号进行特征提取,得到7个特征变量作为IABC-ELM模型的输入,实现刀具磨损监测。范例分析结果表明:选用信号的时域特征和IMF分量的能量比可有效地用于刀具磨损监测;提出的IABC-ELM模型能准确映射所选特征与刀具磨损之间的关系,满足实际需要;输入层权值和隐含层阈值经IABC优化后的ELM表现出更好的预测精度,且其隐含层节点数目明显减小;IABC算法和ABC算法在搜索过程中,IABC算法收敛速度更快且不易陷入局部最优。
| [1] | Kurada S, Bradley C. A review of machine vision sensors for tool condition monitoring[J]. Computers in Industry, 1997, 34(1): 55–72. DOI:10.1016/S0166-3615(96)00075-9 |
| [2] |
谭显春, 刘飞, 曹华军, 等.
面向绿色制造的刀具选择决策模型及其应用[J]. 重庆大学学报, 2003, 26(3): 117–121.
TAN Xianchun, LIU Fei, CAO Huajun, et al. A decision-making framework model of tool selection for green manufacturing and its application[J]. Journal of Chongqing University, 2003, 26(3): 117–121. (in Chinese) |
| [3] |
贺晓辉, 鄢萍, 张佳毅, 等.
功率信息互相关法的刀具破损在线监测[J]. 重庆大学学报, 2011, 34(9): 9–16.
HE Xiaohui, YAN Ping, ZHANG Jiayi, et al. Online tool breakage monitoring method based on power information and cross-correlation algorithm[J]. Journal of Chongqing University, 2011, 34(9): 9–16. DOI:10.11835/j.issn.1000-582X.2011.09.002 (in Chinese) |
| [4] |
高中涛, 刘仁龙.
印刷电路板数控机床断刀检测系统[J]. 重庆大学学报, 2008, 31(3): 290–293.
GAO Zhongtao, LIU Renlong. Data controlling on-break detect system of machine tool base on the print circuit board[J]. Journalof Chongqing University, 2008, 31(3): 290–293. DOI:10.11835/j.issn.1000-582X.2008.03.013 (in Chinese) |
| [5] | Ghosh N, Ravi Y B, Patra A, et al. Estimation of tool wear during CNC milling using neural network-based sensor fusion[J]. Mechanical Systems and Signal Processing, 2007, 21(1): 466–479. DOI:10.1016/j.ymssp.2005.10.010 |
| [6] | Yu J, Liang S, Tang D, et al. A weighted hidden Markov model approach for continuous-state tool wear monitoring and tool life prediction[J]. The International Journal of Advanced Manufacturing Technology, 2016, 91(1/2/3/4): 1–11. |
| [7] | Li B. A review of tool wear estimation using theoretical analysis and numerical simulation technologies[J]. International Journal of Refractory Metals and Hard Materials, 2012, 35: 143–151. DOI:10.1016/j.ijrmhm.2012.05.006 |
| [8] | Brezak D, Majetic D, Udiljak T, et al. Tool wear estimation using an analytic fuzzy classifier andsupport vector machines[J]. Journal of Intelligent Manufacturing, 2012, 23(3): 797–809. DOI:10.1007/s10845-010-0436-x |
| [9] |
关山, 闫丽红, 彭昶.
LS-SVM回归算法在刀具磨损量预测中的应用[J]. 中国机械工程, 2015, 26(2): 217–222.
GUAN Shan, YAN Lihong, PENG Chang. Application ofregression algorithm of LS-SVM in tool wear prediction[J]. China Mechanical Engineering, 2015, 26(2): 217–222. (in Chinese) |
| [10] | Abellan-Nebot J V, Subirón F R. A review of machining monitoring systems based on artificial intelligence process models[J]. International Journal of Advanced Manufacturing Technology, 2010, 47(1): 237–257. |
| [11] | Huang G B, Zhu Q Y, Siew C K. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70(1): 489–501. |
| [12] | Ber A, Kaldor S. The first seconds of cutting, wear behaviour[J]. CIRP Annals-Manufacturing Technology, 1982, 31(1): 13–17. DOI:10.1016/S0007-8506(07)63260-0 |
| [13] | Siddhpura A, Paurobally R. A review of flank wear prediction methods for tool condition monitoring in a turning process[J]. International Journal of Advanced Manufacturing Technology, 2013, 65(1/2/3/4): 371–393. |
| [14] | Karaboga D, Basturk B. Apowerful and efficient algorithm for numerical function optimization:artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459–471. DOI:10.1007/s10898-007-9149-x |
| [15] | Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8(1): 687–697. DOI:10.1016/j.asoc.2007.05.007 |
| [16] | Gao W, Liu S, Huang L. A global best artificial bee colony algorithm for global optimization[J]. Journal of Computational and Applied Mathematics, 2012, 236(11): 2741–2753. DOI:10.1016/j.cam.2012.01.013 |
| [17] | Li X, Lim B S, Zhou J H, et al. Fuzzy neural network modelling for tool wear estimation in dry milling operation[C]//Annual Conference of the Prognotics and Healthe Management Society. 2009: 1-11[2017-12-23]. http://pdfs.semanticscholar.org/1b76/bc902dfa0918adf7ae17e776e2cad2b83feb.pdf. |
| [18] |
裴飞, 陈雪振, 朱永利, 等.
粒子群优化核极限学习机的变压器故障诊断[J]. 计算机工程与设计, 2015(5): 1327–1331.
PEI Fei, CHEN Xuezhen, ZHU Yongli, et al. Transformer fault diagnosis based on particle swarm optimization and kernel-based extreme learning machine[J]. Computer Engineering and Design, 2015(5): 1327–1331. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41


