近年来,湿式离合器在车辆、舰船、工程机械等重要装备中得到了广泛的应用,但工作中湿式离合器常出现打滑、抖动、分离不彻底、发出异响等故障[1-3]。在离合器片间油层分布不均且存在过薄的局部油层时,离合器片分离不平衡或抖动,很容易引发异常磨损,产生局部高温,甚至烧毁离合器片。通过优化离合器的结构参数使离合器片间的最薄油层厚度增大,可以有效减少离合器烧片事故的发生,提高离合器的可靠性。
为保证湿式离合器具有良好的工作性能,一些学者做了大量的优化和可靠性设计研究。Wang等[4-5]构建自动变速器液压系统的动态仿真模型,模拟系统的动态特性,对湿式离合器接合过程进行优化研究,得到了较佳的液压系统相关参数。Depraetere等[6-7]对湿式离合器接合过程的控制方面进行研究,提出了一种在机器正常运行期间学习和调整控制信号的两级优化控制策略。但以上优化研究多局限于接合过程的控制策略方面,而在湿式离合器热流场特性方面的优化研究较少。
在响应面试验设计中,常采用中心组合设计方法来选取试验样本点,并使用旋转设计方法来确定因子水平,进一步设计出合理、高效的试验点安排表[8-11]。但是这些研究一般需要通过查阅手册或者软件来获取试验设计的相关参数,较少有学者推导析因系数、样本点数、因子水平及各水平对应试验次数的具体计算公式。
笔者以脱排结束后处于空转状态的湿式离合器为研究对象,对响应面试验设计中相关参数的计算公式进行推导,并应用于湿式离合器热流场特性的优化设计中,采用不同分析工具获得不同的优化方案,得到湿式离合器的最优结构,进而实现湿式离合器可靠性的优化。
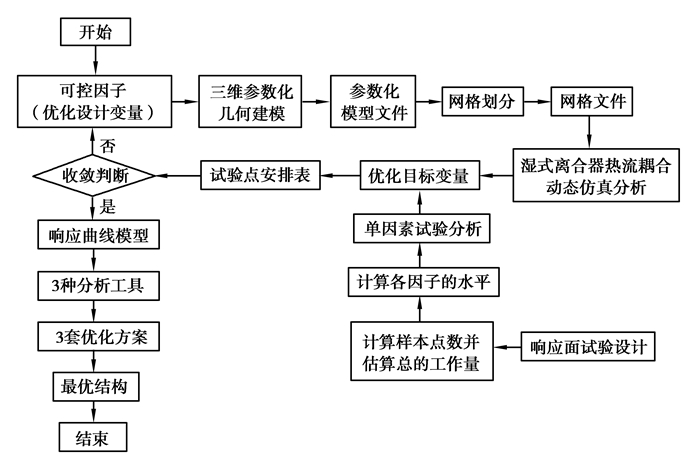
1 湿式离合器的优化设计流程基于响应面试验设计的湿式离合器优化设计流程如图 1所示。
|
图 1 湿式离合器的优化设计流程 Figure 1 Optimal design flow of wet clutch |
1) 在ANSYS Workbench平台下的DesignModeler模块中建立三维实体几何模型,对可控因子进行参数化处理;将湿式离合器模型的参数化几何文件导入到Meshing模块中进行网格划分,得到高质量的网格模型;将生成的网格文件导入CFX软件中进行热流耦合动态仿真分析。
2) 采用响应面试验设计方法来解决非线性数据处理的相关问题,重点对析因系数、样本点数、因子水平及各水平对应试验次数的计算方法进行研究,进而完成对每一个样本点的结构参数取值、每种结构的试验次数的设定,然后根据单因素仿真试验分析方法确定优化目标变量,进一步编排出湿式离合器的试验点安排表。将湿式离合器热流耦合动态仿真计算完成后输出的优化目标值填入试验点安排表,完成一个试验点的计算。判断收敛条件是否满足,若不满足则根据试验点安排表继续进行下一个试验点的计算,直到所有的试验点均计算完成为止,此时达到收敛要求,试验点安排表的全自动循环计算终止。
3) 基于试验点安排表中的实际仿真数据,根据最小二乘法原理拟合出响应曲面模型,分别运用Design Expert、ANSYS Workbench、Excel对湿式离合器进行优化计算,得到3套优化方案,最后筛选出因子水平的最佳组合。
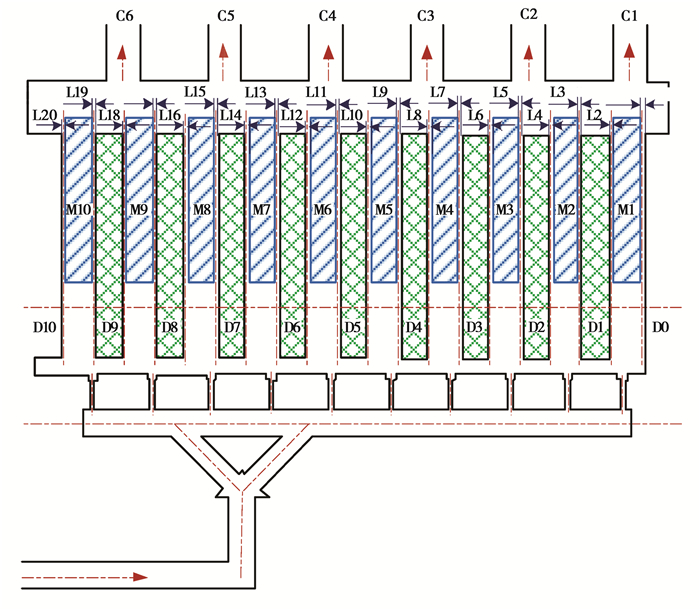
2 基于参数化模型的热流耦合分析湿式离合器润滑油路结构简图如图 2所示,D0~D10为对偶片,其中D0为端盖,D10为活塞;M1~M10为摩擦片;Lm(m=1,2,…,20)分别对应为1~20号片间油层,m为油层编号;Ck(k=1,2,…,6)分别对应为1~6号出油管,k为出油管编号,出油管Ck的孔径大小为dk,且湿式离合器初始结构的出油管孔径均为15 mm。在脱排结束后的空转状态下,工作油缸行程为10 mm,假设平均分配给离合器片之间的间隙,则油层的厚度h均为10/20=0.5(mm)。
|
图 2 湿式离合器润滑油路结构简图 Figure 2 Structure diagram of lubricatingoil circuit of wet clutch |
润滑油最大流速出现在对偶片外缘处,其值为
| $ {v_{\max }} = \omega \cdot {R_{\rm{D}}}, $ | (1) |
式中:RD为对偶片外缘的半径,RD=267 mm;ω为主动轴的角速度。
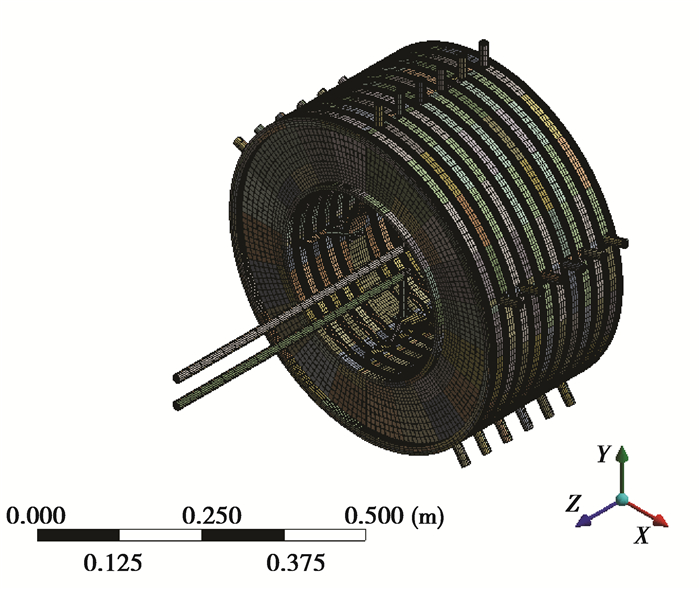
2.1 参数化有限元模型由于外部三维软件建立的实体模型导入到ANSYS Workbench软件时,并不是严格意义上的无缝连接,所以选择在DesignModeler环境下进行几何建模,得到湿式离合器参数化模型。为了尽可能减小网格自动划分对有限元计算结果的影响,达到较高的计算精度要求,在Meshing模块中进行了较为复杂的网格划分操作,得到了高质量的参数化有限元网格模型如图 3所示,共计421 799个节点,389 700个网格。
|
图 3 湿式离合器参数化有限元网格模型 Figure 3 Parametric finite element mesh model of wet clutch |
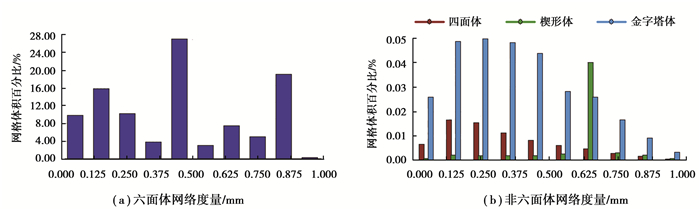
通过网格质量检查,得到湿式离合器参数化有限元网格模型的全局网格度量如图 4所示,横坐标为网格的尺寸大小,纵坐标为特定尺寸范围内的网格占网格总体积的百分比。图中,六面体网格高达网格总体积的99.580%,而四面体网格、楔形网格、金字塔网格分别仅占网格总体积的0.070%,0.054%,0.296%。
|
图 4 全局网格度量 Figure 4 Global grid metrics |
把湿式离合器参数化有限元网格模型导入到CFX软件中,并根据实际工况加载如表 1所示的边界条件。得到的湿式离合器参数化有限元模型如图 5所示。
| 表 1 边界条件 Table 1 Boundary conditions |

|
图 5 湿式离合器参数化有限元模型 Figure 5 Parametric finite element model of wet clutch |
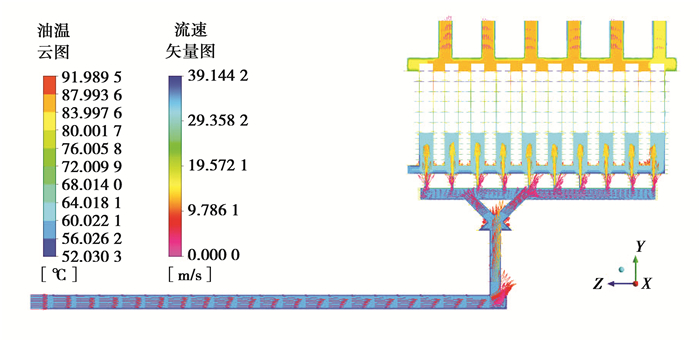
基于计算流体力学理论,对湿式离合器进行热流耦合动态仿真计算,得到离合器初始结构的油温及流速如图 6所示。
|
图 6 湿式离合器的油温及流速 Figure 6 Oil-temperature and flow rate of wet clutch |
由图 6可知,温度场的最高油温Tmax=91.989 5 ℃,出现在19号油层处。取各片间油层的最高温度值表征各油层温度的大小,则片间油层的平均温度Tave=
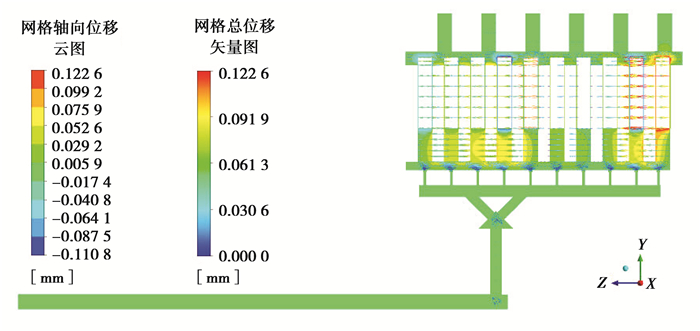
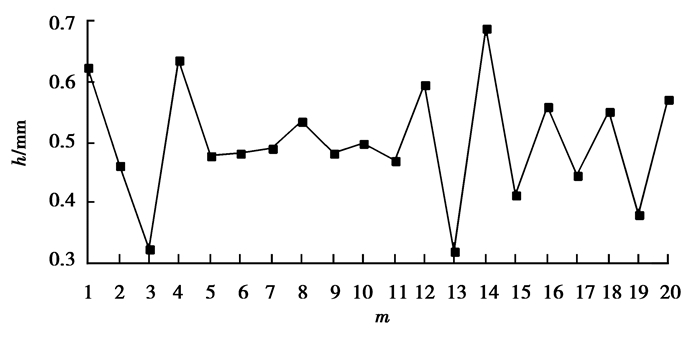
湿式离合器流场轴向位移的大小和方向如图 7所示,离合器片轴向最小位移SZ为负数,即在Z轴负半轴方向上润滑油最大位移值,且SZ=-0.110 8 mm,出现在摩擦片M7处。摩擦片M1向左移动了0.122 6 mm,促使1号油层变厚为0.622 6 mm;摩擦片M7向右移动了0.110 8 mm,对偶片D6向左移动了0.070 0 mm,导致13号油层最薄为hmin=0.319 2 mm;对偶片D7向左移动了0.077 5 mm,导致14号油层最厚为hmax=0.688 3 mm。初始结构的片间油层厚度h的分布情况如图 8所示。
|
图 7 湿式离合器流场轴向位移图 Figure 7 Axial displacement diagram of wet clutch flow field |
|
图 8 初始结构的片间油层厚度分布 Figure 8 Thickness distribution of oil layer between plates in initial structure |
由图 7、8可知,初始结构的湿式离合器片间油层厚度分布极为不均,13号油层和3号油层厚度均较小,容易产生较大的片间油膜承载力和较大的带排转矩[14-16]。在离合器片分离不平衡或抖动时,若油层厚度处于离合器片倾斜抖动范围内,将引发异常磨损,产生局部高温,甚至烧毁离合器片。
根据湿式离合器初始结构热流耦合动态仿真结果可知,离合器的原始结构参数有必要进行优化。即在保证润滑油的最高温度值基本不增大的前提下,增大最薄油层的厚度,从而避免湿式离合器局部油膜承载力过大、带排转矩过大、烧片等工程实际问题,提高离合器的可靠性。
3 响应面试验设计 3.1 响应面数学模型响应面法采用线性多项式来近似隐式极限状态方程,通过试验设计来确定线性多项式的待定系数,从而得到响应面模型,进而预测未试验点的响应值,该方法具有良好的鲁棒性且计算简单。完全二阶多项式响应曲面数学模型可表示为[17-18]:
| $ y = {\alpha _0} + \sum\limits_{i = 1}^n {{\alpha _i}{x_i}} + \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^n {{\alpha _{ij}}{x_i}{x_j}} } + \sum\limits_{i = 1}^n {{\alpha _{ii}}x_i^2} + \varepsilon , $ | (2) |
式中:y为拟合的响应面函数;X=(x1,x2,…,xn)为设计变量;n为设计变量的个数,也即可控因子(用字母f表示)的个数,n≥2;α0,αi,αij,αii分别为常数项、一次项、交叉项、二次项待定回归系数,通过最小二乘回归法拟合确定;ε为随机误差项。
3.2 析因系数及样本点数的计算| $ q = 1 + C_n^1 + C_n^2 + C_n^1 = \frac{1}{2}\left( {n + 1} \right)\left( {n + 2} \right)。$ | (3) |
为求解方程(2)的待定系数,必须满足试验次数N≥q,且每个因子的水平数应大于等于3。在3水平全因子试验设计中,n个因子对应的试验次数为3n,因此试验次数随着因子数呈指数增长,显然会导致剩余自由度过大,即:
| $ n \to + \propto ,\frac{{{3^n}}}{q} \to + \propto 。$ | (4) |
为了减少试验次数,缩短试验时间,并得到有效的试验结果,笔者采用中心组合设计方法在因子空间中选择3类具有不同特征的点,适当组合起来形成试验计划。
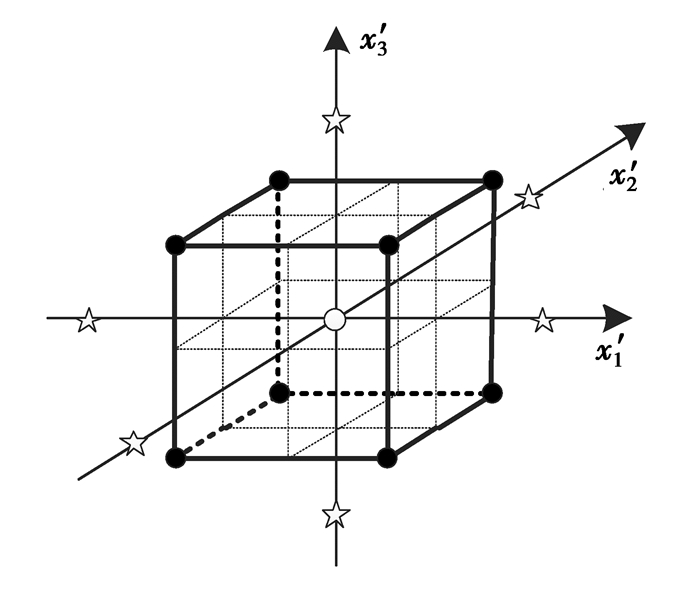
试验次数为N时,所需要的样本点数为N。对于n个因子,样本点由以下3种类型的点构成。因子数为3时的中心组合设计布点示意图如图 9所示。
|
图 9 三因子中心组合设计布点示意图 Figure 9 Schematic layout of three-factor center combination design |
1) 中心点:设定中心点数c=1;
2) 星号点:2n个;
3) 角点:2水平全因子试验(2n个)或其部分实施。
在角点数量为2n时,中心组合设计需要的试验次数为2n+2n+1,n∈{2,3,4}。但是在n≥5时,由于样本点数过大,对于一些耗时的试验,需要消耗大量的人力、物力资源。为了有足够的样本点数来求解回归方程,同时又避免因剩余自由度较大导致试验工作量过大,必须采用部分实施2水平全因子试验的方法对样本点数N进行控制,即通过引进一个析因系数ζ使N/q∈[a,b],a,b为正实数。此时,样本点数为:
| $ N = {2^{n - \zeta }} + 2n + 1。$ | (5) |
则有:
| $ \frac{N}{q} = \frac{{{2^{n - \zeta }} + 2n + 1}}{{\frac{1}{2}\left( {n + 1} \right)\left( {n + 2} \right)}} \in \left[ {a,b} \right]。$ | (6) |
对公式(6)进行变换,得到:
| $ \zeta \in \left[ {{\zeta _{\min }},{\zeta _{\max }}} \right], $ | (7) |
式中:
设定析因系数ζ为自然数,且满足:
| $ \zeta = \left\{ \begin{array}{l} {\rm{ROUND}}\left( {{\zeta _{\max }},0} \right),{\zeta _{\min }} < 0;\\ {\rm{ROUND}}\left( {\frac{{{\zeta _{\min }} + {\zeta _{\max }}}}{2},0} \right),{\zeta _{\min }} \ge 0。\end{array} \right. $ | (8) |
式中:ROUND(x,0)表示对x四舍五入取整数;在ζmin<0时,允许存在ζ=ROUND(ζmax,0)>ζmax的情况。
则:
| $ \zeta = \left\{ \begin{array}{l} {\rm{ROUND}}\left( {n - \log _2^{\left[ {\frac{a}{2}\left( {n + 1} \right)\left( {n + 2} \right) - 2n - 1} \right]},0} \right),{\zeta _{\min }} < 0;\\ {\rm{ROUND}}\left( {n - \frac{1}{2}log_2^{\left[ {\frac{b}{2}\left( {n + 1} \right)\left( {n + 2} \right) - 2n - 1} \right] \cdot \left[ {\frac{a}{2}\left( {n + 1} \right)\left( {n + 2} \right) - 2n - 1} \right]},0} \right),{\zeta _{\min }} \ge 0。\end{array} \right. $ | (9) |
经分析发现,在通常情况下试验点个数N是所求回归项数q的1.5~3.0倍[19],即一般a=1.5,b=3.0,将其代入公式(9)得到:
| $ \zeta = \left\{ \begin{array}{l} {\rm{ROUND}}\left( {n + 2 - \log _2^{\left( {3{n^2} + n + 2} \right)},0} \right),2 \le n \le 6,\\ {\rm{ROUND}}\left( {\frac{{2n + 3 - \log _2^{\left( {3{n^2} + 5n + 4} \right) \cdot \left( {3{n^2} + n + 2} \right)}}}{2},0} \right),n \ge 7。\end{array} \right. $ | (10) |
将公式(10)代入公式(5)得到:
| $ N = \left\{ \begin{array}{l} {2^{n - {\rm{ROUND}}\left( {n + 2 - \log _2^{\left( {3{n^2} + n + 2} \right)},0} \right)}} + 2n + 1,2 \le n \le 6,\\ {2^{n - {\rm{ROUND}}\left( {\frac{{2n + 3 - \log _2^{\left( {3{n^2} + 5n + 4} \right) \cdot \left( {3{n^2} + n + 2} \right)}}}{2},0} \right)}} + 2n + 1,n \ge 7。\end{array} \right. $ | (11) |
式中:根据公式(8),在n=5时,允许存在N/q≈1.286∉[1.5,3.0]的情况。
联立公式(3)、(11),运用求数列极限的相关数学计算方法可以得到:
| $ n \to + \propto ,\frac{N}{q} \in \left( {1.5,3.0} \right]。$ | (12) |
在实际多因子试验设计中,因子数n一般控制在[2, 21]。而对于n∈[22, 50]的大型试验设计,由于N较大,需要占用大量的试验资源,故常采用Min-Run Res V设计的方法确定样本点数。在n=12时,规定ζ=4,此时取c=1,则N=281,N/q≈3.088,公式(10)、(11)不适用。中心点数c表示各可控因子都取零水平的中心点的重复试验次数,提供一致精度和纯误差的估计,一些有限元分析软件(例如ANSYS、ANSYS Workbench等)默认按照c=1来计算样本点数,但一些数理统计分析软件(例如Design Expert、SAS等)还提供了c≠1的计数方式,即在公式(11)计算结果的基础上增加c-1次零水平的中心点重复试验。综上所述,对公式(10)、(11)进行修正,得到中心组合设计中析因系数ζ的计算公式为:
| $ \zeta = \left\{ \begin{array}{l} {\rm{ROUND}}\left( {n + 2 - \log _2^{\left( {3{n^2} + n + 2} \right)},0} \right),2 \le n \le 6;\\ {\rm{ROUND}}\left( {\frac{{2n + 3 - \log _2^{\left( {3{n^2} + 5n + 4} \right) \cdot \left( {3{n^2} + n + 2} \right)}}}{2},0} \right),7 \le n \le 21,n \ne 12,\\ 4,n = 12。\end{array} \right. $ | (13) |
中心组合设计中样本点数N的计算公式为:
| $ N = \left\{ \begin{array}{l} {2^{n - {\rm{ROUND}}\left( {n + 2 - \log _2^{\left( {3{n^2} + n + 2} \right)},0} \right)}} + 2n + c,2 \le n \le 6;\\ {2^{n - {\rm{ROUND}}\left( {\frac{{2n + 3 - \log _2^{\left( {3{n^2} + 5n + 4} \right) \cdot \left( {3{n^2} + n + 2} \right)}}}{2},0} \right)}} + 2n + c,7 \le n \le 21,n \ne 12;\\ 280 + c,n = 12。\end{array} \right. $ | (14) |
通过公式(14)可以计算出与因子数n对应的试验次数N,预估完成全部试验所需要的工作量大小,从而进一步控制整个优化设计所需要的时间。
假设每一次试验所需要的时间均为Δt,则完成全部试验所需要的工作量为:
| $ t = N \cdot \Delta t。$ | (15) |
采用旋转组合设计方法,对每个因子取5个水平。试验设计简图如图 10所示,以(0,±1,±β)编码,(0,0)为中心点,β为星号点对应的极值。
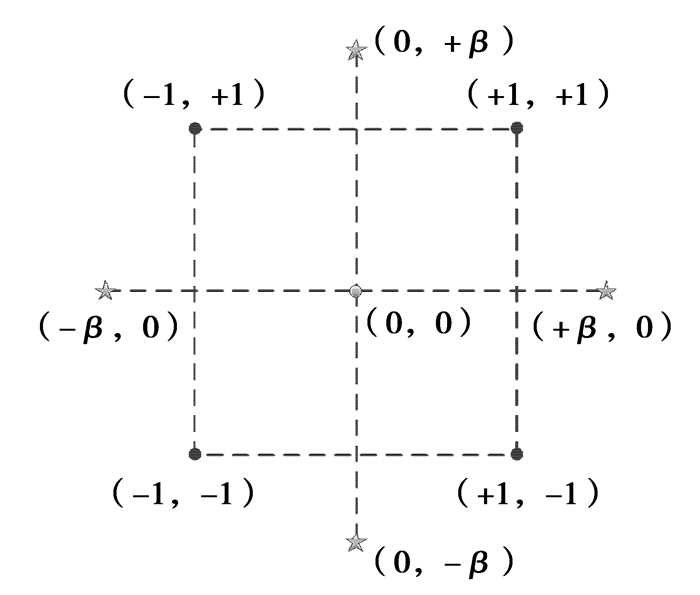
|
图 10 试验设计简图 Figure 10 Diagram of test design |
对文献[20]中β的计算公式进行一定的拓展,可以表示为:
| $ \beta = {2^{\frac{{n - \zeta }}{4}}}。$ | (16) |
可控因子数为n时,因子f的水平及对应的试验次数如表 2所示。表中,f-β、f-1、f0、f+1、f+β的取值可分别表示为:
| $ \left\{ \begin{array}{l} {f_{ - \beta }} = {f_{\min }},\\ {f_{ - 1}} = \frac{{{f_{\min }} + {f_{\max }}}}{2} - \frac{{{f_{\max }} - {f_{\min }}}}{{{2^{\frac{{n - \zeta }}{4} + 1}}}},\\ {f_0} = \frac{{{f_{\min }} + {f_{\max }}}}{2},\\ {f_{ + 1}} = \frac{{{f_{\min }} + {f_{\max }}}}{2} + \frac{{{f_{\max }} - {f_{\min }}}}{{{2^{\frac{{n - \zeta }}{4} + 1}}}},\\ {f_{ + \beta }} = {f_{\max }}。\end{array} \right. $ | (17) |
| 表 2 因子f的水平及对应的试验次数 Table 2 Level and corresponding test times of factor f |
根据6个出油管孔径的实际取值范围,设计6组仿真试验如下:
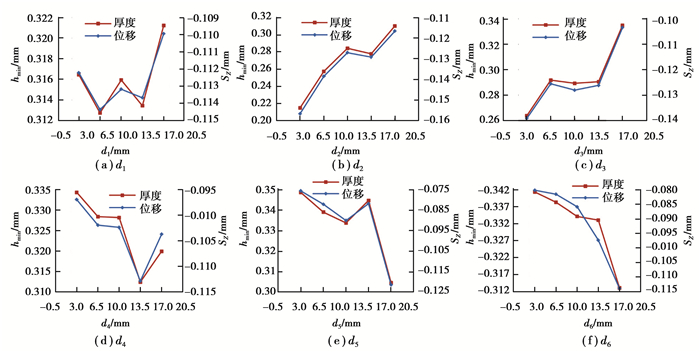
在d2~d6均为15 mm不变的条件下,d1分别取3.0,6.5,10.0,13.5,17.0 mm,对湿式离合器的这5种结构分别进行热流耦合动态仿真分析,得到的最薄油层厚度hmin及离合器片轴向最小位移SZ如图 11(a)所示。同理,分别对d2~d6进行分析,得到d2~d6对hmin与SZ的影响关系分别如图 11(b)~(f)所示。
|
图 11 d1~d6对最薄油层厚度与离合器片轴向最小位移的影响 Figure 11 Effect of d1~d6 on thickness of thinnest oil layer and minimum axial displacement of clutch plates |
由图 11可知,最薄油层厚度hmin与离合器片轴向最小位移SZ的变化规律基本一致。在这30次试验中,温度场最高油温始终维持在91 ℃~93 ℃。由此可见,各个出油管的孔径对于片间润滑油的流场分布具有较大的影响,而对油温分布的影响较小。当出油管孔径在一定范围内取值时,可以通过增大SZ值来间接获得较大的hmin值。
5 湿式离合器优化策略 5.1 设计变量、目标变量及约束条件的确定 5.1.1 设计变量选择出油管的孔径d1~d6为设计变量。在不影响湿式离合器整体工作性能的前提下,确定设计变量的最佳取值范围为:
| $ {d_k} \in \left[ {{f_{\min }},{f_{\max }}} \right], $ | (18) |
综合考虑初始结构参数和离合器热流场特性,当dk=14 mm时,热流场分布情况较好,以f0=14 mm为零水平,在小范围内取值fmin=11 mm,fmax=17 mm。
根据公式(13)(14)(16),取中心点数c=2,则:析因系数ζ=1;试验次数N=46;星号点对应的极值β=2.378 414。
根据表 2及公式(17),可以得到因子dk的水平及对应的试验次数如表 3所示。
| 表 3 因子dk的水平及对应的试验次数 Table 3 Level and corresponding test times of factor dk |
通过单因素仿真试验分析发现,最小油层厚度hmin总是出现在与轴向位移较小的离合器片相邻的油层处,且一般情况下,SZ越大,会促使最小油层厚度hmin有变大的趋势。同时,由图 2可知,在SZ增大时,会促使轴向位移最小的离合器片右边的平均油层厚度增大,有利于流场的均匀分布。另外,在ANSYS Workbench平台下,以SZ值为目标变量时,能够很方便地实现试验点安排表的全自动循环计算。因此,取离合器片轴向最小位移SZ为目标变量。
5.1.3 约束条件根据实际的流场、温度场的分布特性,确定设计变量和响应变量需要满足的约束条件为:
| $ \left\{ \begin{array}{l} {S_Z} \in \left[ {{{\underline S }_Z},0} \right),\\ {{S'}_Z} \in \left( {0,{{\overline {S}' }_Z}} \right],\\ {T_{\max }} \in \left( {{T_0},{{\overline {T}' }_{\max }}} \right],\\ {T_{{\rm{ave}}}} \in \left( {{T_0},{{\overline {T}' }_{{\rm{ave}}}}} \right],\\ {{P'}_k} \in \left( {{{P'}_{\min }},{{P'}_{\max }}} \right),\\ {d_k} \in \left[ {{{f'}_{\min }},{{f'}_{\max }}} \right]。\end{array} \right. $ | (19) |
式中:SZ为SZ的下限约束值;S′Z为离合器片轴向最大位移,S′Z为S′Z的上限约束值;T0为入口油温;T′max、T′ave分别为Tmax、Tave的上限约束值;P′k为第k个出油管的入口处最大油压;P′min、P′max分别为设定的润滑油路流场最小油压、最大油压;f′min、f′max分别表示在求解出响应面拟合模型后进行优化分析时dk的最小值、最大值,且fmin≤f′min<f′max≤fmax;取f′min=f-1,f′max=f+1。
5.2 响应面优化根据已确定的因子、水平、试验次数,以代码的形式编排试验表,试验时再转变为实际操作值,获得响应变量SZ的观测值。在ANSYS Workbench平台下进行试验点全自动循环计算,试验设计方案及计算得到的优化目标值如表 4所示,且在所有样本点中,Tmax∈[91, 93] ℃,可见最高油温的波动范围较小。
| 表 4 试验点安排表(编码) Table 4 Test Points Arrangement Table (Code) |
运用Design Expert软件对表 4中的46个点的试验数据进行方差分析[21]。通过剔除对响应值影响不显著的一部分交叉项和二次项,实现对拟合模型的优化。方差分析表如表 5所示。
| 表 5 方差分析表 Table 5 Variance Analysis Table |
由表 5可知,模型项P<0.000 1,说明该模型是极显著的。失拟项的平方和非常趋近于0,且失拟项P=0.123 7>0.05,说明所得方程与实际拟合中非正常误差所占比例小,回归模型的拟合效果较好。另外,x1~x6的P值按照由小到大排列后依次为:x5,x2,x6,x3,x1,x4。
回归方程拟合模型为:
| $ \begin{array}{*{20}{l}} {{S_Z} = - 1.38762 + 0.018178{x_1} + 0.038699{x_2} + 0.044375{x_3} + 5.17168{x_4} \times {{10}^{ - 4}}}\\ {\;\;\;\;\;\;\;\;\;\; + 0.058174{x_5} + }\\ {\;\;\;\;\;\;\;\;0.029862{x_6} - 1.15494{x_1}{x_5} \times {{10}^{ - 3}} - 1.14708{x_2}{x_3} \times {{10}^{ - 3}} + 1.06066{x_5}{x_6}} \\ \;\;\;\;\;\;\;\;\times {{10}^{ - 3}} - \\ {\;\;\;\;\;\;\;\;6.93766x_2^2 \times {{10}^{ - 4}} - 9.04877x_3^2 \times {{10}^{ - 4}} - 2.38822x_5^2 \times {{10}^{ - 3}} - 1.70488x_6^2} \\ \;\;\;\;\;\;\;\;\times {{10}^{ - 3}}。\end{array} $ | (20) |
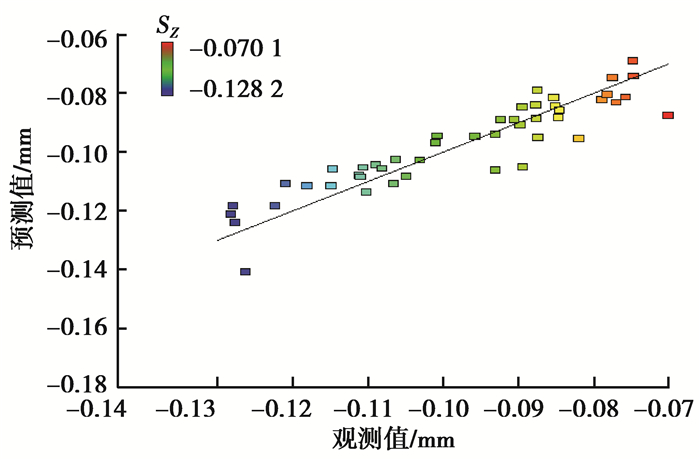
通过该拟合模型得到的预测值与表 4中通过实际仿真计算得到的观测值对比情况如图 12所示。由图可知,运用Design Expert软件得到的拟合模型预测效果较好。
|
图 12 预测值与观测值对比图(Design Expert) Figure 12 Comparison between predicted and observed values (Design Expert) |
根据公式(19)设置约束条件,为保证拟合精度,取拟合效果最精确的曲面部分进行优化分析,即dk∈[12.738 7,15.261 3] mm。
基于回归方程(20),分别采用Design Expert软件、Excel软件,以SZ最大为目标进行优化,分别得到优化方案1和2。
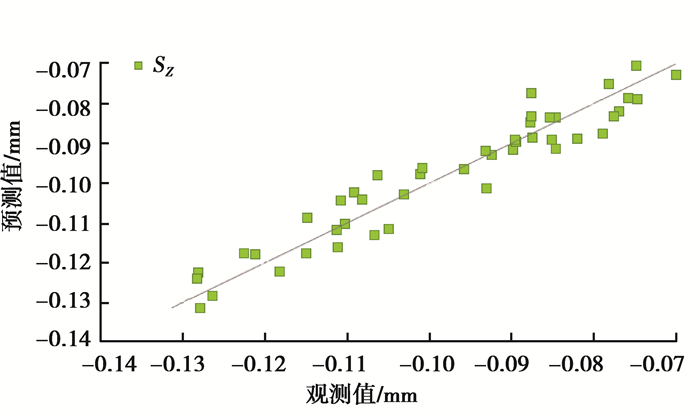
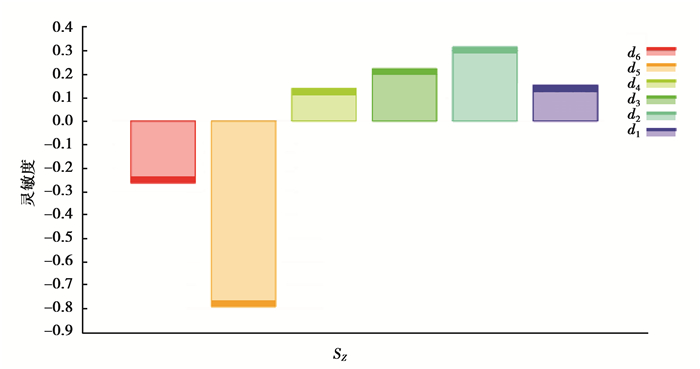
取中心点数c=1,则试验次数N=45。采用ANSYS Workbench软件对表 4中的1~45号点进行分析,得到响应面拟合模型的预测值与表 4中通过实际仿真计算得到的观测值对比情况如图 13所示,由图可知,该拟合模型的预测效果较好。湿式离合器的热流耦合是一个非线性变化的过程,考虑到影响设计变量的不确定性均处于同一个数量级,且各设计变量之间的交互作用会对目标变量产生一定的影响,因此可以通过全局灵敏度分析法[22]得到6个出油管孔径对于SZ大小的影响,全局灵敏度如图 14所示。由图可知,按照x1~x6对SZ的影响由大到小排列后依次为:x5,x2,x6,x3,x1,x4,与使用Design Expert软件分析得到的排列顺序是一致的。以零水平f0=14 mm为基准,为了获得更大的SZ,可以在一定范围内适当增大x1,x2,x3,x4的同时,减小x5,x6。以SZ最大为目标进行优化,得到优化方案3。
|
图 13 预测值与观测值对比图(ANSYS Workbench) Figure 13 Comparison between predicted and observed values (ANSYS Workbench) |
|
图 14 全局灵敏度 Figure 14 Global sensitivity |
根据方案1~3的结构参数,分别进行湿式离合器热流耦合动态仿真计算,得到的响应值如表 6所示。
| 表 6 优化方案 Table 6 Optimization scheme |
在3套方案对比择优时,由于湿式离合器的优化中采用了通过增大离合器片轴向最小位移SZ来间接增大离合器片间最薄油层厚度hmin的优化思路,应着重考虑hmin的实际增长幅度。由表 6可知,与初始结构相比较,3套优化方案均具有一定的优化效果,其中优化方案3的实际仿真值SZ,hmin分别增加了0.042 6和0.060 1 mm,二者的增长幅度均大于另外两套优化方案,优化效果最为明显。因此,选择方案3作为最优结构。
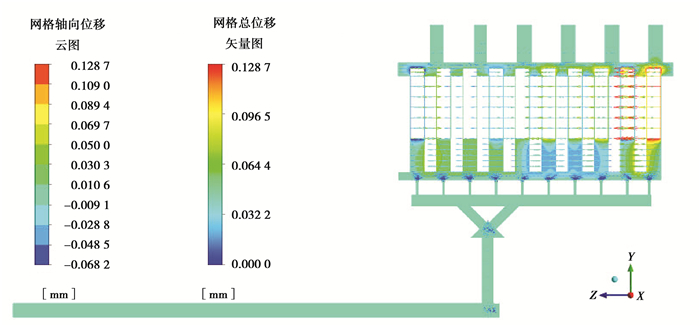
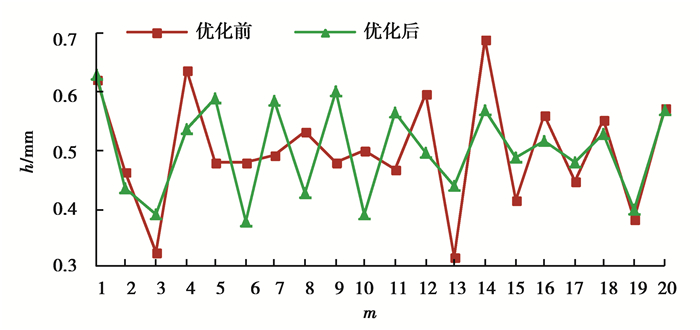
5.3 最优结构优化后的湿式离合器流场轴向位移、片间油层厚度分布分别如图 15、16所示。
|
图 15 优化后的湿式离合器流场轴向位移图 Figure 15 Axial displacement diagram of flow field in wet clutch after optimization |
|
图 16 优化前后的片间油层厚度分布 Figure 16 Thickness distribution of oil layer between plates before and after optimization |
由图 15、16可知,SZ增大了38.472%;最小油层厚度出现在6号油层,且hmin=0.379 3 mm,增大了18.828%。另外,Tmax,Tave分别降低了0.436%、0.014%,可见对油温的影响不大。因此,经过优化后,湿式离合器烧片事故发生的可能性得到了降低,提高了离合器的可靠性能。
6 结论1) 根据湿式离合器的结构特征,构建了参数化几何模型,通过复杂的网格划分操作,建立了六面体网格体积高达99.580%的高质量参数化有限元模型,基于计算流体力学理论,对湿式离合器进行了热流耦合动态仿真分析,得到了片间油层、润滑油温的分布情况。
2) 分析中心组合设计方法的采样原理,推导出了析因系数、样本点数、因子水平及各水平对应试验次数的具体计算公式,解决了通过查阅手册或软件获取相关参数的不便,具有一定的实用性。
3) 根据单因素仿真试验分析方法确定了以离合器片轴向最小位移为目标变量的优化思路,间接优化了最小油层厚度。
4) 基于最小二乘法求解出响应面拟合模型,采用3种分析工具对湿式离合器进行优化,得到了3套优化方案,实现了湿式离合器设计参数动态优化,提高了湿式离合器的可靠性能,为相关产品提供了可供参考的优化策略。
笔者对中心组合设计方法中常涉及到的样本点数和析因系数做了公式推导,并对星号点极值的一般计算公式进行了改善,给出了因子水平及各水平对应试验次数的计算公式。经逐一检验,这些公式完全适用于ANSYS、ANSYS Workbench、Design Expert等分析软件。把这些计算方法应用于响应面试验设计中,通过3种优化方法对比选优以确保较好的优化效果,这种优化策略具有一定的实用性。但旋转设计法对于因子数的取值范围具有一定的限制,如何设计出一种对因子个数没有限制的采样方法,还需要进一步研究。
| [1] | Chen M, Ma B. Fault diagnosis of wet-shift clutch based on STFT and wavelet[J]. Advanced Materials Research, 2011, 301/302/303: 1560–1567. |
| [2] |
姚运勋. (某型)客车离合器故障研究[D]. 北京: 北京化工大学, 2015. YAO Yunxun. Research on clutch fault of certain bus[D]. Beijing: Beijing University of Chemical Technology, 2015. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2976710 |
| [3] |
张凤莲. 不均匀接触对湿式离合器滑摩、分离与冷却特性影响研究[D]. 北京: 北京理工大学, 2016. ZHANG Fenglian. Study on the effect of uneven contact on vehicle multidisc wet clutch sliding, separating and cooling[D]. Beijing: Beijing Institute of Technology, 2016. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10007-1016716997.htm |
| [4] | Wang S, Xu X, Liu Y, et al. Dynamic characteristic simulation of AT hydraulic system[C]//Sae International Powertrains, Fuels and Lubricants Congress. Boston: SAE Technical Paper, 2008: 63-68. https://doi.org/10.4271/2008-01-1683. |
| [5] | Lei Y, Li X, Liang W, et al. Hydraulic system optimization and dynamic characteristic simulation of double clutch transmission[J]. Procedia Environmental Sciences, 2011, 10(Part B): 1065–1070. |
| [6] | Depraetere B, Pinte G, Broeck L V D, et al. A two-level optimization based learning control strategy for wet clutches[J]. IFAC Proceedings Volumes, 2010, 43(10): 54–59. DOI:10.3182/20100826-3-TR-4015.00013 |
| [7] | Depraetere B, Pinte G, Symens W, et al. A two-level iterative learning control scheme for the engagement of wet clutches[J]. Mechatronics, 2011, 21(3): 501–508. DOI:10.1016/j.mechatronics.2011.01.002 |
| [8] | Juraeva M, Song D J, Ryu K J. An optimum design study of the yarn-channel shape of the air-interlacing nozzle by analysis of fluid flow[J]. Textile Research Journal, 2012, 82(5): 474–483. DOI:10.1177/0040517511435008 |
| [9] |
王春林, 彭海菠, 丁剑, 等.
基于响应面法的消防泵S型叶片改进优化设计[J]. 机械工程学报, 2013, 49(10): 170–177.
WANG Chunlin, PENG Haibo, DING Jian, et al. Optimization for S-type blade of fire pump based on response surface method[J]. Journal of Mechanical Engineering, 2013, 49(10): 170–177. (in Chinese) |
| [10] |
夏玉峰, 杨建兵, 田永生, 等.
基于响应面法的汽车离合器盘毂温锻-冷精整工艺多目标优化[J]. 中南大学学报(自然科学版), 2015(9): 3203–3210.
XIA Yufeng, YANG Jianbing, TIAN Yongsheng, et al. Multi-object optimization of warm forging-cold sizing technology for automobile clutch disc-hub based on response surface model[J]. Journal of Central South University (Science and Technology), 2015(9): 3203–3210. DOI:10.11817/j.issn.1672-7207.2015.09.006 (in Chinese) |
| [11] |
代翠, 孔繁余, 董亮, 等.
基于响应面法的离心泵作透平水力和声学性能优化[J]. 农业工程学报, 2015, 31(15): 40–47.
DAI Cui, KONG Fanyu, DONG Liang, et al. Hydraulic and acoustic property optimization for centrifugal pump as turbine based on response surface method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(15): 40–47. DOI:10.11975/j.issn.1002-6819.2015.15.006 (in Chinese) |
| [12] | Marklund P, Maki R, Larsson R, et al. Thermal influence on torque transfer of wet clutches in limited slip differential applications[J]. Tribology International, 2007, 40(5): 876–884. DOI:10.1016/j.triboint.2006.09.004 |
| [13] | Hu J, Peng Z, Yuan S. Drag torque prediction model for the wet clutches[J]. Chinese Journal of Mechanical Engineering, 2009, 22(2): 238–243. DOI:10.3901/CJME.2009.02.238 |
| [14] | Meng Q R, Hou Y F. Effect of oil film squeezing on hydro-viscous drive speed regulating start[J]. Tribology International, 2010, 43(11): 2134–2138. DOI:10.1016/j.triboint.2010.06.008 |
| [15] | Wang Y, Li Y, Ning K Y, et al. Modeling and analysis of wet clutch engagement characteristics[J]. Journal of Chongqing University (English Edition), 2015(1): 1–8. |
| [16] |
郑海峰. 湿式离合器带排转矩建模及影响因素分析[D]. 吉林: 吉林大学, 2017. ZHENG Haifeng. Drag torque modeling and analysis of wet clutch[D]. Jilin: Jilin University, 2017. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10183-1017160569.htm |
| [17] |
徐中明, 吕伟东, 夏小均, 等.
面向行人安全的保险杠结构改进优化[J]. 重庆大学学报, 2017, 40(4): 1–8.
XU Zhongming, LYU Weidong, XIA Xiaojun, et al. Bumper structure optimization for pedestrain leg protection[J]. Journal of Chongqing University, 2017, 40(4): 1–8. (in Chinese) |
| [18] | Tang X, Luo J, Liu F. Aerodynamic shape optimization of a transonic fan by an adjoint-response surface method[J]. Aerospace Science & Technology, 2017, 68: 26–36. |
| [19] | Ahn J, Kim H J, Lee D H, et al. Response surface method for airfoil design in transonic flow[J]. Journal of Aircraft, 2011, 38(38): 231–238. |
| [20] | Buree S L, Giunta A A, Balabanov V, et al. A coarse grained parallel variable-complexity multidisciplinary optimization paradigm[J]. International Journal of Supercomputer Applications and High Performance Computing, 1995, 10(4): 269–299. |
| [21] |
徐向宏, 何明珠. 试验设计与Design-Expert、SPSS应用[M]. 北京: 科学出版社, 2010.
XU Xianghong, HE Mingzhu. Experimental design and the application of design-expert and SPSS[M]. Beijing: Science Press, 2010. (in Chinese) |
| [22] |
刘万刚, 邬晓敬, 叶正寅, 等.
空气舵颤振特性的不确定性及全局灵敏度分析[J]. 振动工程学报, 2017, 30(2): 255–261.
LIU Wangang, WU Xiaojing, YE Zhengyin, et al. Uncertainty and global sensitivity analysis of flutter characteristics for air rudder[J]. Journal of Vibration Engineering, 2017, 30(2): 255–261. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41


