装配方案设计是产品进行装配的前提和基础,是决定装配质量的重要因素[1]。不同设计方案对产品质量、成本和精度等方面的影响不同,一个好的设计方案不仅应该满足产品所有的几何约束、精度要求,还应缩短装配过程的时间,减少装配成本[2],而且随着制造业的发展,装配过程可靠性也越来越受重视。装配方案设计时一般会存在多个可行方案,从中优选出最佳的装配方案对产品生产过程尤为重要。
传统的装配设计方案优选一般由工程师凭借经验完成[3]。而随着产品功能越来越多样化,其结构也越来越复杂,可行装配序列数量越来越多,装配要求也越来越高,即使经验丰富的工程师也难以在若干可行装配方案中优选出最佳方案。因此,对装配设计方案进行评价就显得尤为重要。目前,有很多学者对装配方案评价方法进行了研究:周思航等[4]提出基于装配方案尺寸变动度建立偏差传递模型,通过评价各装配方案的累积偏差确定出最佳的装配方案;赵磊等[5]提出用装配并行性、子装配体稳定性等定量指标和装配难易度、开敞性等定性指标相结合的方式,用模糊理论实现对装配方案的评价;曹鹏彬等[6]提出从装配方便性、可行性、精度保证性等方面出发,使用最优参考集和定量计算结合的方法获取评价指标的隶属度,实现对装配过程的评价;张嘉易[7]等针对影响装配工艺性的因素,提出单元级和整体级评价指标,通过定义最优参考序列实现对装配方案的评价;Lu等[8]提出从装配方案花费时间、人力等方面出发,使用软件模拟不同方案所需花费的成本,实现对方案的评价。上述理论或方法多是以装配成本、精度或效率为主要因素对装配方案进行评价,考虑因素比较单一,且忽略了可靠性因素。而如今机械产品的综合质量要求越来越高,稳定性和可靠性也成为衡量产品质量的关键因素。因此,装配方案优选时不仅需要考虑精度、成本、工艺等因素,还需考虑方案的可靠性和稳定性,以便对装配方案进行全面评价,实现装配设计方案的优选。
基于以上分析,提出一种基于粗糙集知识简约的装配设计方案多属性评价方法,从精度、稳定性、可靠性、成本、操作简单性等方面构建评价指标体系,并利用粗糙集简约知识对评价指标进行简约,保留必要指标。首先,通过相关文献的收集、整理,获取装配设计方法评价指标;然后利用粗糙集对评价指标进行知识简约,保留必备的评价指标,并求出必备指标的模糊权重;最后,根据必备评价指标的属性值以及相应权重,利用逼近于理想值的排序方法(technique for order preference by similarity to ideal solution, TOPSIS)对可行装配设计方案进行评价,以获取最佳的装配方案。
1 装配设计方案多属性决策评价模型优选装配设计方案时要综合考虑不同装配方案对各种评价指标影响程度,因此,装配设计方案优选的过程属于多属性决策评价过程,要想优选出最佳装配方案就需要对可行装配方案进行合理评价。设可行装配设计方案集B={B1, B2, …, Bm},Bi(i=1, 2, …, m)表示第i个可行装设计方案;设计方案的评价指标集C={c1, c2, …, cn},cj(i=1, 2, …, n; )表示第j个评价指标;评审专家集E={e1, e2, …, er},es(i=1, 2, …, r)表示第s个评审专家。针对传统装配设计方案评价指标过多,可能存在冗余且实用性不强的特点,在确定出评价指标以后,利用粗糙集的简约知识对评价指标进行简约,剔除冗余指标,简化了方案评价过程。在装配设计方案的多属性决策过程中,为了充分利用专家经验,综合考虑设计方案,将通过粗糙集获得的简约指标权重融入TOPSIS方法中,分析各装配设计方案的优劣,以实现对方案的排序并优选出最佳的装配设计方案。基于粗糙集的装配设计方案多属性决策评价模型如图 1所示。

|
图 1 基于粗糙集的装配设计方案多属性决策评价模型 Figure 1 Multi attribute decision making model of assembly design scheme based on Rough Set |
在装配设计方案评价指标确定以后,众多指标可能存在冗余,且在确定装配序列评价指标权重的过程中,评价指标间关系的不确定性较强。粗糙集理论是波兰数学家Pawalak提出的一种数据分析理论[9],其能够有效分析不精确、不一致、不完整等不完备信息,还可以对数据进行分析和推理[10-11]。目前,粗糙集一般有两种应用:一是对评价对象进行有效分类,其属性简约能保证在除去冗余属性之后,并不影响原有的分类效果[12],在冗余属性除去后,保留必要的属性,有效地减少了评价过程的工作量,增强评价方法实用性;二是能够有效处理具有模糊性、不一致性和不确定性的问题。基于以上特点用粗糙集来确定装配序列评价指标的权重,可以降低主观因素以及信息模糊性对评价过程的影响,而且粗糙集不需要任何先验知识或额外数据信息就可以确定粗糙集的属性重要性[13],这克服了传统不确定信息处理过程需要先验知识或额外数据的缺陷,比层次分析法、模糊综合评价法等能更好地处理信息不确定性问题。
2.1 属性简约为方便讨论,应用粗糙集理论对装配序列评价指标进行简约时,做如下定义:
定义1 决策信息系统I=(U, C, V, f)。其中U={u1, u2, …, u|U|}表示样本(对象或实体)数据的集合,且U≠∅,称为论域;C为一个有限非空属性集合,C={c1, c2, …, c|n|}是所有属性的集合;V=
定义2 设I=(U, C, V, f)是一个信息系统,c∈C,如果ind(C-{c})=ind(C),则称c在C中是不必要的;否则称c在C中是必要的。不必要的属性在信息系统中是多余的,将其从信息系统中删去,不会改变信息系统的分辨能力,相反,如果从信息系统中删除一个必要的属性,则一定会改变信息系统的分辨能力。
对指标进行初步简约后,需要利用区分函数对剩余指标进行简约。
定义3 设有信息系统I,ci(ei)是记录ei在属性ci上的值,Cij表示分辩矩阵中第i行,第j列的元素,Cij被定义为
| $ {C_{ij}} = \left\{ \begin{array}{l} \left\{ {c \in C\left| {{c_i}\left( {{e_i}} \right) \ne {c_i}\left( {{e_j}} \right)} \right.} \right\},D\left( {{e_i}} \right) \ne D\left( {{e_j}} \right);\\ 0,D\left( {{e_i}} \right) = D\left( {{e_j}} \right); \end{array} \right. $ | (1) |
其中,i, j=1, 2, …, n; n=|U|;ci为第i个评价指标;ci(ei)为专家ei对指标ci优良性的评价结果;D(ei)为指标评价值的属性集,表示专家ei对指标ci优良性评价值的集合。
区分矩阵是从分辨矩阵构造的。一个数据的所有简约可以通过构造分辨矩阵并且化简由分辨矩阵导出的区分函数得到,在使用吸收律化简区分函数成标准式后,所有蕴含式包含的属性就是信息系统的所有简约集合[14]。
2.2 评价指标的简约评价指标体系是评价装配设计方案的基础,不同的评价指标对装配方案评价过程的影响是不同的,甚至会影响评价结果。因此,对方案进行评价时,指标的选取遵循全面、合理和实用的原则,确定出的指标不仅要能够反映装配方案特征,而且还要能够较方便获取数据,以便实现装配方案的评价。
在企业调研基础上结合工程实际,从工艺、可靠性、精度、成本和稳定性5个方面出发,通过对大量参考文献进行收集、分析,整理出16项对产品装配序列有影响的评价指标:装配序列可靠度(c1)、重新装配次数(c2)、装配过程失效率(c3)、操作难度(c4)、装配操作并行性(c5)、装配关系数(c6)、装配精度自修正性(c7)、零件参与尺寸链数量(c8)、装配基准数(c9)、装配综合能力指数(c10)、紧固件装配靠前性(c11)、重力方向装配次数(c12)、紧固对间夹持零件数(c13)、夹装变换次数(c14)、重定向次数(c15)、装配操作聚合性(c16)。在此需要说明的是,评价指标是评价装配设计方案的基础,在选取评价指标时,参照对象为一般机械产品,而对某些具有特殊性产品的装配设计方案进行评价时,可在本文的基础上针对具体产品适当添加或者删减相应指标,以便对产品装配方案做出更加合理的评价。例如重型机械设备,装配时零件质量对于产品的装配过程有一定的影响,质量越大的零件优先装配比较合理,因此,在评价重型机械设备的装配设计方案时,可将“零件质量”作为评价指标。
为了能够有效地提取必要的评价指标,邀请10位专家作为评价集体E=(e1, e2, …, e10);设计方案评价指标共有16个,构成条件属性集C={c1, c2, c3, …, c16};利用专家知识对指标评价效果的优良性作出评价,评价结果以“优、良、中、差”4个等级分类,并用4、3、2、1数值表示。邀请10位专家分别对装配设计方案16个初始评价指标做出评价,评价结果如表 1所示。
| 表 1 装配设计方案各初始评价指标专家评分数据 Table 1 Expert evaluation data of each initial evaluation index of assembly design |
由上表可知,指标c2和指标c8的专家评价结果相同,根据粗糙集知识,属性相同的指标具有相同的分辨能力,则只需保留一个指标,因此,可将指标c2简约。同理,亦可将指标c9, c11, c14约简。利用区分矩阵法对剩余指标进行约简,如表 2所示。
| 表 2 评价指标区分矩阵 Table 2 Discernibility matrix of evaluation index |
利用逻辑吸收率计算区分矩阵内的元素可得指标体系的简约集:{c1, c5, c7, c10, c15},即利用粗糙集简约算法简约后的评价指标分别为:装配序列可靠度(c1)、装配操作并行性(c5)、装配精度自修正性(c7)、装配综合能力指数(c10)、重定向次数(c15)。在此,为了方便必要指标的后续分析,对5个必要指标按顺序重新进行编号为:C1, C2, C3, C4, C5。
2.3 评价指标含义及计算方法定义第i个装配设计方案的第j个评价指标的属性值为cij,则各评价指标的定义和属性值计算如下:
1) 装配序列可靠度C1。指装配序列在规定的时间和条件下,装配出的产品具有规定可靠性的能力。借鉴文献[15]的方法,通过分析装配方案各工步的装配正常率,求解各个方案的装配过程可靠度。设有n个装配工步,Pci表示第i道工步的正常概率,PRj表示完成第j道工步时装配序列的正常概率,则装配序列的可靠度属性值ci1为
| $ {c_{i1}} = \prod\limits_{j = 1}^m {{P_{Rj}}} \prod\limits_{i = m + 1}^n {{P_{ci}}} , $ | (2) |
式中:j=1, 2, …, m;i=m+1, m+2, …, n;
2) 操作并行性C2。指实施装配序列时,可以同时进行装配的子装配体数量与总装配操作数的比重,其属性值ci2越大,可以同时进行装配的子装配体数量也就越大,装配过程也越简单。用树形结构表示装配顺序时,其深度越小,装配方案可同时进行装配的子装配体也就越多,装配序列也就越好。其属性值ci2可以用装配树深度值差值法表示为
| $ {c_{i2}} = \left( {{t_{\max }} - {t_i}} \right)/\left( {{t_{\max }} - {t_{\min }}} \right), $ | (3) |
式中:tmax为可行装配序列装配树的最大深度值;tmin为最小深度值;ti为当前装配顺序深度值。
3) 装配精度自修正性C3。在装配过程中,产品精度指标的保障是依靠轴孔特征的装配而逐步实现的,且多级装配过程有一定的精度自修正性,即后续装配操作可以修正前序的装配误差,以致保证装配过程的精度,因此,定义装配序列的误差修正系数表示装配过程的精度保证性。设装配序列有s各关键孔位特征的精度样本,定义装配序列的误差修正能力系数为
| $ {c_{i3}} = \left( {\sum\limits_{i = 1}^s {\frac{{i \times \left( {\left| {{d_{i1}}} \right| - \left| {{d_{in}}} \right|} \right)}}{{{\rm{sig}}\left( {\mathop {\max }\limits_j {D_i}\left( j \right)} \right)\mathop {\max }\limits_j {D_i}\left( j \right)}}} } \right)/\sum\limits_{i = 1}^s i , $ | (4) |
式中:i=1, 2, …, s; j=1, 2, …, n;
4) 装配综合能力指数C4。装配序列的稳定性常用装配过程综合工序能力指数Cpk来衡量。装配序列单工序能力指数Cpki用其轴孔特征量的异常和波动表示:Cpki=
由于装配体的最终装配质量是若干道工序综合决定的,设装配过程有n道工序,Cpki为第i道工序的能力指数,定义装配序列的综合能力指数为
| $ {c_{i4}} = \sum\limits_{i = 1}^n {{C_{pki}}{w_i}} , $ | (5) |
其中i=1, 2, …, n;wi为利用层次分析法获取的第i道工序的权重值。
5) 重定向次数C5。指装配体在装配过程中装配方向改变的次数。其值越小,装配过程的时操作数量也就越少,则装配效率越高。因此,装配时其值越小越好。其属性值ci5等于装配操作过程中配方向改变的次数。
2.4 评价指标权重的确定评价指标之间具有一定的不确定性和模糊性,因此,可利用粗糙集确定装配序列评价指标的权重ωj。对于指标体系中的指标Cj∈C(j=1, 2, …, n), 衡量指标Cj对于指标体系C的重要度,可以由体系C中去掉指标Cj之后所引起的信息量变化的大小来度量[16]。采用粗糙集方法对评价指标的处理步骤如下:
步骤1 信息系统I=(U, C, V, f)中,P⊆C,U/ind(P)={X1, X1, …, Xn}, 知识P的信息量定义为
| $ I\left( P \right) = \sum\limits_{i = 1}^n {\frac{{\left| {{X_i}} \right|}}{{\left| U \right|}} \times \left( {1 - \frac{{\left| {{X_i}} \right|}}{{\left| U \right|}}} \right)} = 1 - \frac{1}{{{{\left| U \right|}^2}}}\sum\limits_{i = 1}^n {\left| {X_i^2} \right|} , $ | (6) |
式中:Xi为除去某项评价指标后,剩余评价指标的集合;|Xi|为集合Xi的基数;
步骤2 求指标Cj在指标体系中的重要性。指标Cj(Cj∈C)的重要度可以理解为从评价指标集中去掉指标Cj,然后考虑其决策评价结果大小的变化程度,变化越大说明指标Cj越重要,指标Cj在指标体系C中重要性SigC-{Cj}(Cj)可表示为
| $ {\rm{Si}}{{\rm{g}}_{C - \left\{ {{C_j}} \right\}}}\left( {{C_j}} \right) = I\left( C \right) - I\left( {C - \left\{ {{C_j}} \right\}} \right)。$ | (7) |
当C=(Cj)时,用Sig(Cj)表示Sigφ(Cj):
| $ {\rm{Sig}}\left( {{C_j}} \right) = {\rm{Si}}{{\rm{g}}_\varphi }\left( {{C_j}} \right) = I\left( C \right) - I\left( \varphi \right) = I\left( C \right) - I\left( {\left\{ {{C_j}} \right\}} \right), $ | (8) |
式中:U/IND(φ)={U},I(φ)=0。
步骤3 求指标Cj的权重。指标Cj(Cj∈C)的权重可以理解为从评价指标集中去掉指标Cj,然后考虑其决策评价结果大小的变化程度,变化越大说明指标Cj越重要。
| $ {\omega _j} = \frac{{{\rm{Si}}{{\rm{g}}_{C - \left\{ {{C_j}} \right\}}}\left( {{C_j}} \right)}}{{\sum\limits_{j = 1}^n {{\rm{Si}}{{\rm{g}}_{C - \left\{ {{C_j}} \right\}}}\left( {{C_j}} \right)} }} = \frac{{I\left( C \right) - I\left( {C - \left\{ {{C_j}} \right\}} \right)}}{{nI\left( C \right) - \sum\limits_{j = 1}^n {I\left( {C - \left\{ {{C_j}} \right\}} \right)} }}, $ | (9) |
步骤4 指标权重归一化。将各指标的权重面向归一化处理,得到各指标的权重为
| $ {\omega _j} = \frac{{{\rm{Sig}}\left( {{C_j}} \right)}}{{\sum\limits_{j = 1}^n {{\rm{Sig}}\left( {{C_j}} \right)} }}, $ | (10) |
式中ωj为第j个评价指标经过粗糙集处理后的初始权重。
3 基于改进TOPSIS的方案评价评价装配设计方案的目的是帮助设计人员从可行方案中优选出最佳方案,综合前文分析可知装配设计方案的评价过程属于多目标综合决策问题。目前,逼近于理想值的排序方法(technique for order preference by similarity to ideal solution, TOPSIS)是解决该类问题的主要方法,其中心思想是综合各方案评价指标的最优属性值和最劣属性值建立理想解和负理想解,然后计算各方案与理想解和负理想解的贴近度,若方案距离理想解最近,且距离负理想解最远,则该方案最佳,反之,则方案最差[17-20]。
然而,TOPSIS方法中应用的指标权重大多为专家主观确定的精确值,其准确性较低。为了解决TOPSIS方法的这一缺陷,提出用改进TOPSIS方法确定装配序列关键评价指标重要性,其主要表现为运用粗糙集理论确定各评价指标较为合理的模糊权重,应用模糊权重代替专家主观确定的精确值,然后根据评价指标的属性值对各方案进行综合评价。
基于改进TOPSIS法的装配序列评价流程如下所示:
步骤1 建立决策矩阵
设在装配设计方案Bi(i=1, 2, …, m)下,指标Cj(j=1, 2, …, n)的取值为cij,则决策矩阵为D=[cij]m×n。
步骤2 规范化决策矩阵。由于装配设计方案各指标间的属性不同,为了使不同属性之间可以相互比较,需将各类型指标进行无量化处理。建立规范化决策矩阵Z=[zij]m×n,其中zij=cij/
步骤3 构造加权规范化矩阵。根据粗糙集确定出的评价指标权重,结合设计方案规范化决策矩阵Z中评价指标的属性值,得到加权规范化决策矩阵Vij=[vij]m×n=[zij×ωj]m×n,其中ωj为第j个评价指标的权重,i=1, 2, …, m,j=1, 2, …, n。
步骤4 确定理想解和负理想解。评价指标的属性可以分为两类:效益型属性值J和成本型属性值J′,效益型指标值越大越好,成本型指标值越小越好。两类指标的理想解和负理想解的表达式分别为
| $ {B^ + } = \left\{ {v_1^ + ,v_1^ + , \cdots ,v_j^ + , \cdots ,v_n^ + } \right\} = \left\{ {\left( {\mathop {\max }\limits_i {v_{ij}}\left| {j \in J} \right.} \right),\left( {\mathop {\min }\limits_i {v_{ij}}\left| {j \in J'} \right.} \right)} \right\},\\ j = 1,2, \cdots ,m。$ | (11) |
| $ {B^ - } = \left\{ {v_1^ - ,v_1^ - , \cdots ,v_j^ - , \cdots ,v_n^ - } \right\} = \left\{ {\left( {\mathop {\max }\limits_i {v_{ij}}\left| {j \in J} \right.} \right),\left( {\mathop {\min }\limits_i {v_{ij}}\left| {j \in J'} \right.} \right)} \right\},\\ j = 1,2, \cdots ,m。$ | (12) |
步骤5 计算各方案的距离尺度。各可行装配设计方案到理想解和负理想解的距离分别为
| $ S_i^ + = \sqrt {\sum\limits_{j = 1}^n {{{\left( {{v_{ij}} - v_j^ + } \right)}^2}} } ,S_i^ - = \sqrt {\sum\limits_{j = 1}^n {{{\left( {{v_{ij}} - v_j^ - } \right)}^2}} } , $ | (13) |
式中:Si+和Si-分别为装配设计方案Ai到最优方案和最劣方案的欧式距离;vj+和vj-分别为第j个评价指标下的最优目标和最劣目标;vij为第i个装配设计方案在第j个指标下的加权规范值。
步骤6 计算各方案到理想解的贴近度。装配设计方案到理想解的相对贴近度表示为
| $ C_i^ + = \frac{{S_i^ - }}{{\left( {S_i^ - + S_i^ + } \right)}}, $ | (14) |
式中0<Ci+<1。Ci+值越大,方案Ai距离最优方案越近,则该装配设计方案越优。按照Ci+的值排序,可得所有装配设计方案的优劣排序情况。
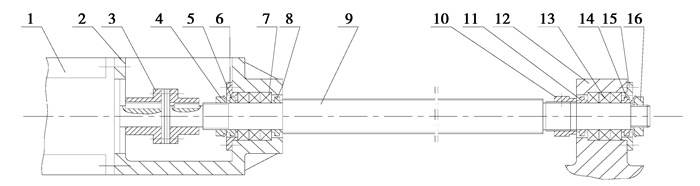
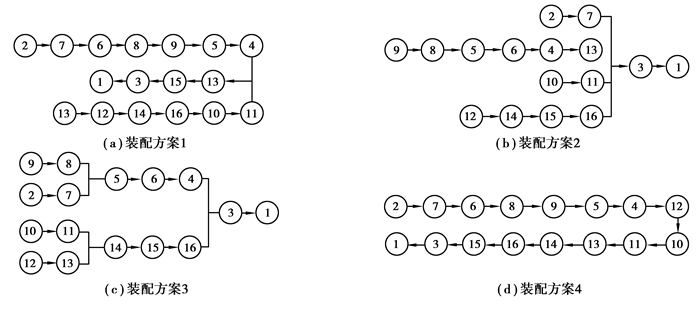
4 案例分析以下对某企业产品的传动系统装配设计方案为例进行分析。该企业的车削中心和加工中心所采用的传动系统基本一致,结构如图 2所示。2种机床传动系统装配方案由各自车间的工艺员制定,由于不同的工艺员操作习惯和装配理念不同,因此,目前传动系统共有4种不同的装配方案,如图 3所示。现对4种装配序列进行综合评价,从中优选出最佳的装配方案。
|
图 2 传动系统装配图 Figure 2 Drive system assembly drawing 1.电机; 2.电机座; 3.联轴器; 4.锁紧螺母; 5.隔套; 6.端压盖; 7.左轴承; 8.隔套; 9.滚珠丝杆; 10.锁紧螺母; 11.隔套; 12.丝杆座; 13.右轴承; 14.隔套; 15.端压盖; 16.锁紧螺母 |
|
图 3 可行装配方案 Figure 3 Feasible assembly scheme |
步骤1 确定评价指标属性值
针对4个装配设计方案,建立装配设计方案集B={B1, B2, B3, B4}。根据第2节确定的评价指标和指标的计算方法,求得各装配设计方案的评价指标属性值,各指标的基本属性值如表 3所示。
| 表 3 评价指标属性值初始数据 Table 3 Initial data of attribute value of evaluation index |
步骤2 权重计算
设去除指标{C1后的指标集为X1={C2, C3, C4, C5},
同理,可求得其他指标的权重:SigX2(C2)=
归一化指标权重可得:
| $ {\omega _1} = 0.14,{\omega _2} = 0.246,{\omega _3} = 0.14,{\omega _4} = 0.323,{\omega _5} = 0.14。$ |
步骤3 装配设计方案的综合模糊评价
由表 2可知4种装配设计方案的各项评价指标属性值量化数据,由于指标C1, C2, C3, C4属于极大型指标,C5属于极小型数据,为了消除不同数据间量纲的差异,对表 3数据进行量纲归一化处理,结果如表 4所示。
| 表 4 评价指标属性值归一化处理后数据 Table 4 The attribute value of evaluation index is normalized after data processing |
根据步骤2所求各项指标权重,可得加权化规范矩阵,同时可确定成本型指标和效益型指标的理想解和负理想解,结果如表 5所示。
| 表 5 加权标准化决策矩阵 Table 5 Weighted standardized decision matrix |
计算各可行装配设计方案到理想方案和负理想方案的距离Si+、Si-,并计算各方案与理想解的贴近程度Ci+, 结果如表 6所示。
| 表 6 装配设计方案评价结果 Table 6 The evaluation result of Assembly designs |
各方案与理想解贴近度Ci+数值从大到小的排序结果代表了各装配设计方案的优劣程度,因此,4个装配设计方案的优良程度为:B2>B3>B1>B4。
4.2 结果分析由模糊层次分析法、模糊综合评价法和TOPSISI法3种方法得到的排序结果如表 7所示。在此,利用模糊层次分析法分别对简约前和简约后指标进行了评价。在指标简约前对方案进行评价时,需要分析16项评价指标的权重和属性值,然后得到装配设计方案的优良性排序结果,其工作量较大,计算复杂;在指标简约后利用模糊层次分析法对方案进行评价时,需要重新邀请若干位专家对5项指标进行评价,且评价、计算的过程较为繁杂;模糊综合评价法是在保持评价指标和指标权重不变的情况下,计算各设计方案的隶属度评价矩阵,进而实现对方案的综合评价。
| 表 7 各方案的评价结果对比 Table 7 Comparison of the evaluation results of each scheme |
从4种评价结果可以看出,采用模糊层次分析法对指标简约前16项评价指标计算的结果与本文所提出的利用粗糙集简约知识所计算的方案评价结果一致,即采用16项评价指标和采用5项核心评价指标具有相同的评价效果,这验证了粗糙集知识简约后的核心指标具有较强代表性,也说明了该方法的有效性。同时,采用模糊层次分析法对指标简约后5项评价指标的计算结果与本文所提出的利用粗糙集简约知识所计算的方案评价结果一致,即采用不同的指标权重求解方法所求得的装配设计方案评价结果一致,这排除了不同指标权重求解方法对装配设计方案评价结果的影响,也说明了本方法的有效性;同时,在使用粗糙集方法获取评价指标的权重时,可直接通过专家对指标的评价结果(见表 1)获取,不必再通过专家打分,与模糊层次分析法相比更简单,这增强了该方法的实用性;采用模糊综合评价法的评价时,评价出的最优设计方案出现不一致,最后经过车间的反复试验发现,B2设计方案装配难度较小、精度较高,且装配时间上较短。最终,装配方案B2获得了企业的认可,并指导产品的装配,证明了该方法的实用性。
5 结论1) 根据文献调研提出装配设计方案的评价指标体系,并使用粗糙集对评价指标进行简约,保留核心评价指标,有效地减小了评价过程的工作量,增强了方法的实用性。
2) 根据核心评价指标的属性值和模糊权重,利用TOPSIS获取装配设计方案的理想方法和负理想方案,通过计算待评估方案与最佳、最劣方案的贴近度,甄选出了最佳的装配设计方案。
3) 该方法可以为复杂机电产品装配设计方案的优选提供参考。不同类别的产品可以根据其自身特点对评价体系进行修改,以致实现复杂产品装配设计方案的评价,为装配方案优选提供建议。
4) 在今后的装配设计方案评价过程中,可以考虑建立评价模型系统,实现评价数据的标准化输出和输出,以快速地获取装配设计方案的评价。
| [1] |
顾廷权, 高国安, 徐向阳, 等.
装配工艺规划中装配序列生成与评价方法研究[J]. 计算机集成制造系统, 1998, 4(1): 25–27.
GU Yanquan, GAO Guoan, XU Xiangqian, et al. Research on assembly sequence generation and evaluation method in assembly process planning[J]. Computer Integrated Manufacturing System, 1998, 4(1): 25–27. (in Chinese) |
| [2] |
刘翊, 李世其, 王俊峰, 等.
产品分层分级的交互式拆卸装配序列规划[J]. 计算机集成制造系统, 2014, 20(4): 785–792.
LIU Yi, LI Shiqi, WANG Junfeng, et al. Interactive disassembly approach for assembly sequence planning based on product hierarchical-classification[J]. Computer Integrated Manufacturing Systems, 2014, 20(4): 785–792. (in Chinese) |
| [3] | Lazzerini B, Marcelloni F. A genetic algorithm for generating optimal assembly plans[J]. Artificial Intelligence in Engineering, 2000, 14(4): 319–329. DOI:10.1016/S0954-1810(00)00011-X |
| [4] |
周思航, 刘振宇, 谭建荣.
基于尺寸变动度的装配序列偏差传模型及质量评价方法[J]. 机械工程学报, 2011, 47(2): 1–8.
ZHOU Sihang, LIU Zhenyu, TAN Jianrong. Deviation propagation model of assembly sequence and quality evaluation approach based on degree of dimensional variation[J]. Journal of Mechanical Engineering, 2011, 47(2): 1–8. (in Chinese) |
| [5] |
赵磊, 李原, 张开富, 等.
改进的复杂产品装配顺序模糊评价方法[J]. 中国机械工程, 2009, 20(13): 1533–1537.
ZHAO Lei, LI Yuan, ZHANG Kaifu, et al. An improved assembly sequence fuzzy evaluation method for complex products[J]. China Mechanical Engineering, 2009, 20(13): 1533–1537. DOI:10.3321/j.issn:1004-132X.2009.13.005 (in Chinese) |
| [6] |
曹鹏彬, 曹立峰.
齿轮泵装配过程的综合评价[J]. 武汉工程大学学报, 2012, 34(4): 47–52.
CAO Pengbin, CAO Lifeng. Comprehensive evaluation of assembly process of gear pump based on optimal reference set[J]. Journal of Wuhan Industry and Technology, 2012, 34(4): 47–52. (in Chinese) |
| [7] |
张嘉易, 王成恩, 马明旭, 等.
产品装配序列评价方法建模[J]. 机械工程学报, 2009, 45(11): 218–224.
ZHANG Jiayi, WANG Chengen, MA Mingxu, et al. Modeling of the method of product assembly sequence evaluation[J]. Journal of Mechanical engineering, 2009, 45(11): 218–224. (in Chinese) |
| [8] | Lu C, Fuh J Y H, Wong Y S. Evaluation of product assemblability in different assembly sequences using the tolerancing approach[J]. International Journal of Production Research, 2006, 44(23): 5037–5063. DOI:10.1080/00207540600579656 |
| [9] | Skowron A. Rough sets and boolean reasoning[J]. Information Sciences, 2007, 177(1): 41–73. DOI:10.1016/j.ins.2006.06.007 |
| [10] | Wang C, Shao M, Sun B, et al. An improved attribute reduction scheme with covering based rough sets[J]. Applied Soft Computing, 2015, 26(C): 235–243. |
| [11] |
王宏图, 黄振华, 范晓刚, 等.
粗糙集-神经网络理论在矿井通风系统评价中的应用[J]. 重庆大学学报, 2011, 34(9): 90–94.
WANG Hongtu, HUANG Zhenhua, FAN Xiaogang, et al. The application od rough setsneural network theory to mine ventilation system evalutaion[J]. Journal of Chongqing University, 2011, 34(9): 90–94. DOI:10.11835/j.issn.1000-582X.2011.09.014 (in Chinese) |
| [12] |
李远远. 基于粗糙集的指标体系的构建及综合评价方法研究[D]. 武汉: 武汉理工大学, 2009. LI Yuanyuan. Research on index system construction and comprehensive evaluation method based on rough sets[D]. Wuhan: Wuhan Industry and Technology University, 2009. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1559713 |
| [13] | Chebrolu S, Sanjeevi S G. Attribute Reduction on continuous data in rough set theory using ant colony optimization metaheuristic[C]//International Symposium on Women in Computing and Informatics. Aluva, Indian: ACM, 2015: 17-24. |
| [14] |
王彪, 段禅伦. 粗糙集与模糊集的研究与应用[M]. 电子工业出版社, 2008: 6-9.
WANG Biao, DUAN Chanlun. The research and application of rough sets and fuzzy sets[M]. Publishing House of Electronics Industry, 2008: 6-9. (in Chinese) |
| [15] |
张根保, 崔有志, 柳剑, 等.
Go-flow法在产品装配过程可靠性分析中的应用[J]. 计算机应用研究, 2011, 28(11): 4199–4201.
ZHANG Genbao, CUI Youzhi, LIU Jian, et al. Application of Go-flow methodology in reliability analysis of product ass-embly process[J]. Application Research of Computers, 2011, 28(11): 4199–4201. DOI:10.3969/j.issn.1001-3695.2011.11.053 (in Chinese) |
| [16] | Pawlak Z. Rough sets[J]. International Journal of Information and Computer Science, 1982(11): 341–256. |
| [17] | Zyoud S H, Fuchs-Hanusch D. A bibliometric-based survey on AHP and TOPSIS techniques[J]. Expert Systems with Applications, 2017, 78: 158–181. DOI:10.1016/j.eswa.2017.02.016 |
| [18] | Mousavi-Nasab S H, Sotoudeh-Anvari A. A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems[J]. Materials and Design, 2017, 121: 237–253. DOI:10.1016/j.matdes.2017.02.041 |
| [19] | Sunil C. Hybrid FAHP-TOPSIS approach for performance evaluation of the V down perforated baffle roughened rectangular channel[J]. Energy, 2015, 84: 432–442. DOI:10.1016/j.energy.2015.03.007 |
| [20] |
段其昌, 吴冠霖, 张从力.
基于Internet的三峡库区水质监测模型与监测点布点[J]. 重庆大学学报, 2006, 29(9): 126–129.
DUAN Qichang, WU Guanli, ZHANG Congli. Water quality monitoring model and monitoring point distribution in the Three Gorges Reservoir area based on Internet[J]. Journal of Chongqing University, 2006, 29(9): 126–129. DOI:10.11835/j.issn.1000-582X.2006.09.029 (in Chinese) |
 2018, Vol. 41
2018, Vol. 41


