瓦斯事故是煤矿的重要灾害之一,而瓦斯抽采是防治瓦斯灾害的重要措施。井下顺层瓦斯抽采是高瓦斯矿井最常用的技术手段[1-2],但煤层顺层抽采钻孔的布置对瓦斯抽采效果具有重要影响,抽采钻孔间距过大或过小,都将严重影响瓦斯抽采与采掘的协调关系,且制衡着投入的人力物力及安全生产[3-4]。因此,根据煤层的瓦斯渗透特性,分析煤层瓦斯抽采有效距离,进而科学地布置抽采钻孔,提高瓦斯抽采效率,是实现煤层快速消突的重要举措[3]。
煤层渗透率是反映煤层瓦斯渗流特性及运移规律的重要物性参数之一。煤层在经过漫长地质年代后,具有层理特性[5-6],且层理间一般具有大致平行的裂隙面,即割理[7-8]。由于层理和割理裂隙面差异,其对瓦斯的渗透性影响显著[8-11]。Koenig等[12]的测试结果表明,平行层理方向的渗透率与垂直层理方向的渗透率达到17:1;Wang等[13],Li等[5]的试验测试结果表明,煤层渗透率及变形受层理、节理影响十分显著。
在煤层瓦斯抽采有效半径及钻孔布置研究方面,Lin等[14]针对不同变质程度煤层,采用流固耦合模型进行了有效抽采半径的计算分析。一些学者基于煤层渗流场和变形方程的耦合关系,数值分析了不同地质条件下煤层瓦斯有效抽采半径[15-18]。而在现场,压降法和瓦斯流量法被用来测试煤层瓦斯有效抽采半径[19-20]。以上研究均取得了有益的成果,但这些研究均考虑煤层均值,而实际是煤的各向渗透异性将导致瓦斯抽采有效半径在不同方向上存在差异,岳高伟等[21]针对各向异性煤层的不同钻孔方位,分析了有效抽采半径的差异,但未对各向异性煤层的合理抽采钻孔布置进行研究。
为了揭示各向渗透异性对瓦斯抽采有效半径的影响规律,以及与钻孔布置和预抽时间的关系,在九里山煤矿进行了各向渗透异性煤层有效抽采半径原位测试,而后,在瓦斯压力0.5~2.5 MPa下测试煤芯的渗透率。最后,基于煤层各向渗透异性,建立煤层瓦斯气固耦合渗透模型,数值分析了瓦斯抽采过程中煤层瓦斯压降规律,获得煤层不同方向上的有效抽采半径,并与现场实测数据比较,进而对煤层钻孔布置间距及钻孔数进行优化分析。
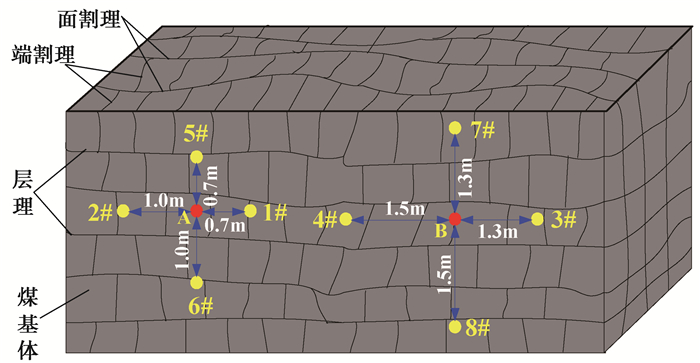
1 煤层各向渗透异性瓦斯抽采有效半径测试 1.1 试验钻孔布置为了保证测试数据的可靠性,在焦作九里山矿二1煤层16141运输巷进行现场测试(煤层厚约7 m,瓦斯压力1.21 MPa),测试地点选择在无瓦斯异常带的原始煤层,且煤层的层理和节理明显。如图 1所示,煤层层理间存在近似正交的裂隙,测试孔孔径为94 mm,孔深约40 m。
|
图 1 现场测试钻孔设计示意图 Figure 1 Schematic diagram of borehole design in field test |
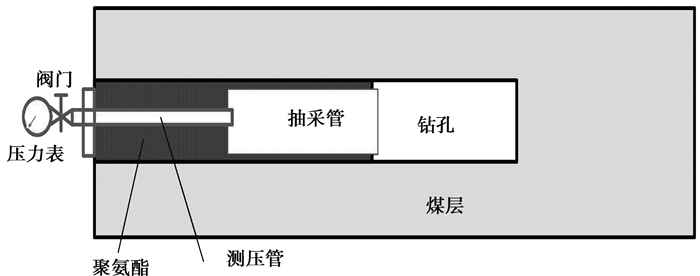
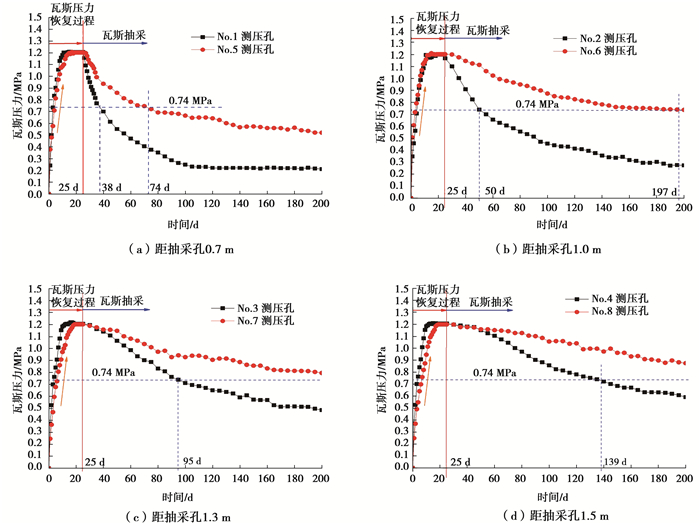
测压孔如图 2所示,其包括成孔、封孔、安装压力表等。而后施工抽采孔。抽采过程中,观察测压孔的压力,并绘制压力-时间变化曲线,如图 3所示。
|
图 2 煤层测压装置 Figure 2 Device of pressure measurement in coal seam |
|
图 3 瓦斯压力测试曲线 Figure 3 Gas pressure curves of test drilling |
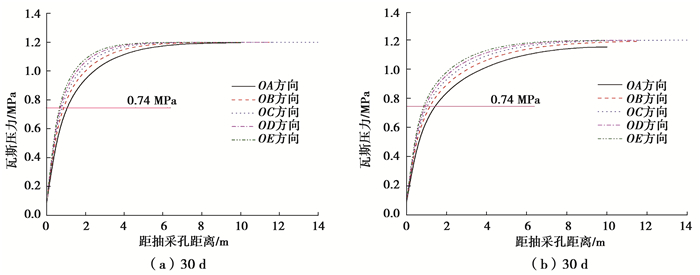
基于AQ 1026—2006 《煤矿瓦斯抽采基本指标》的规定,现以煤层瓦斯抽采过程中瓦斯压力降至0.74 MPa为标准,则测试过程中,测压孔测得的瓦斯压力低于0.74 MPa时,此测压孔至抽采孔的距离即为此抽采时段内的有效抽采半径[3, 22]。
在抽采负压为30 kPa下,不同测压孔测得的瓦斯压力随抽采时间的关系如图 3所示。从图 3可以看出,测压孔瓦斯压力在前25 d处于恢复和稳定阶段(未抽采)。当开始抽采瓦斯(第26天),测压孔测得的瓦斯压力开始随抽采时间的增加而逐渐减小。距离抽采孔越近,测压孔瓦斯压力下降越快。并且随抽采时间增加,煤层瓦斯压力降至0.74 MPa的测压孔距离越远,即有效抽采距离具有时效特征(如表 1所示)。
| 表 1 抽采孔瓦斯压力降至0.74 MPa时间 Table 1 Time of gas pressure dropping to 0.74 MPa |
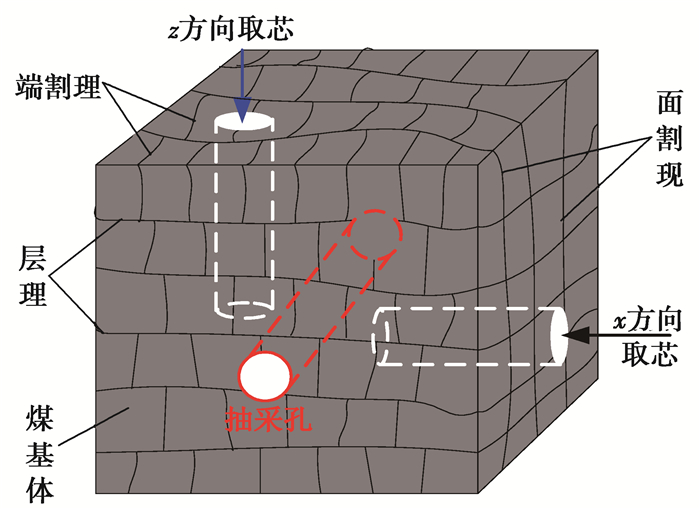
试验所用煤样取自现场测试工作面,煤样块运至实验室后采用取芯机按图 4所示方向取芯,试验煤样尺寸ϕ50 mm×100 mm,经过打磨后即可用来测试平行层理方向(x方向)和垂直层理方向(z方向)的渗透率,分别用kx和kz表示。
|
图 4 试样取芯 Figure 4 Sampling core |
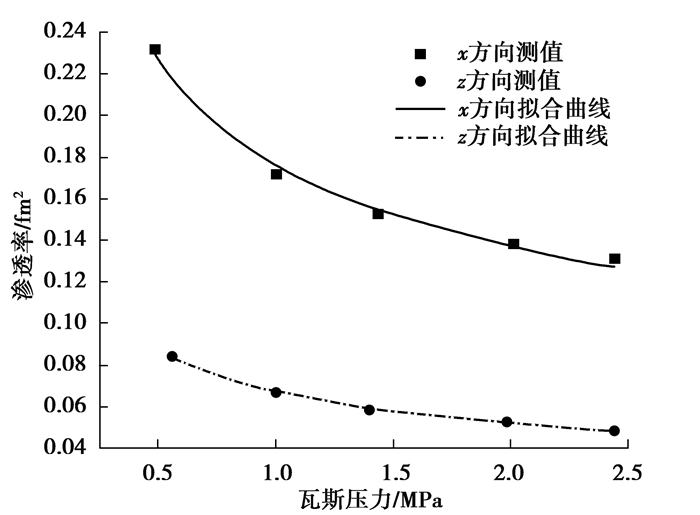
采用达西稳定流方法,煤样渗透率测试采用受载煤岩瓦斯渗流试验系统[23]。基于煤层地应力特征,试验时施加的轴压和围压均为9.6 MPa,则不同方向煤样瓦斯渗透率如图 5所示[23-24]。从图 5可以看出,各试样的渗透率均随瓦斯压力增大呈幂指数减小。渗透率和瓦斯压力的关系可表示为:
|
图 5 煤样渗透率测试结果 Figure 5 Test results of permeability for coal samples |
| $ x方向\;\;\;{k_x} = 0.176\;3{p^{-0.364}}, \left( {{R^2} = 0.990\;6} \right), $ | (1a) |
| $ z方向\;\;\;{k_x} = 0.067\;5{p^{-0.373}}, \left( {{R^2} = 0.998\;9} \right), $ | (1b) |
式中:x和z方向渗透率分别为kx、kz,fm2;p为压力,MPa。
从图 5还可以看出,平行层理方向的渗透率比垂直层理方向的大得多。在相同瓦斯压力下,平行层理方向的渗透率(面割理方向)约为垂直层理方向渗透率的2.6倍。这充分证明了煤层中瓦斯渗流各向异性,且差别十分明显。
3 瓦斯渗流煤体变形基本理论煤基体具有复杂的孔隙结构,瓦斯在煤层中的渗流过程中,计算模型作如下假设[25]:顶底板渗透率为0;煤体只发生弹性变形;瓦斯压力较低,考虑为理想气体;瓦斯在煤层中的渗流服从达西定律;瓦斯在煤层中流动为等温过程。
3.1 煤层瓦斯赋存在煤层的孔隙结构中,瓦斯以吸附态和游离态存在,则总的瓦斯含量可表示为[26]
| $ Q = \frac{{abp{\rho _0}{\rho _{\text{s}}}}}{{1 + bp}}\frac{{1-{A_{{\text{ad}}}}-{M_{{\text{ad}}}}}}{{1 + 0.31{M_{{\text{ad}}}}}} + \frac{{{\rho _{\text{f}}}}}{{{p_0}}}p\varphi, $ | (2) |
式中:Q为单位质量煤体中瓦斯含量,m3 /t;p0和p分别为初始瓦斯压力和抽采过程中瓦斯压力,MPa;a、b为Langmuir常数;Mad和Aad分别为煤体的水分和灰分,%;ρs、ρ0和ρf分别为煤的密度、标准条件下瓦斯密度和压力p时瓦斯密度,kg/m3;φ为煤的孔隙率,%。
3.2 煤体孔隙率及渗透率煤层瓦斯抽采过程中,由于瓦斯流动,煤体原应力状态发生变化,煤体孔隙率和渗透率随煤基体的变形而改变。煤的孔隙率φ与初始孔隙率φ0、煤基体体积应变εv、煤体积模量ks和瓦斯压力改变量Δp相关,其函数关系为[4, 15-17]
| $ \varphi = 1-\left( {1-\Delta p/{k_{\text{s}}}} \right)\left( {1-{\varphi _0}} \right)/\left( {1 + {\varepsilon _{\text{v}}}} \right)。$ | (3) |
基于Kozeny-Carman方程,煤层渗透率和孔隙率的动态变化方程为[16]
| $ k = \frac{{{k_0}}}{{1 + {\varepsilon _{\text{v}}}}}{\left[{1 + \frac{{{\varepsilon _{\text{v}}} + \Delta p\left( {1-{\varphi _0}} \right)/{k_{\text{s}}}}}{{{\varphi _0}}}} \right]^3}, $ | (4) |
式中k0为煤体的初始渗透率,m2。
3.3 煤体变形基于煤体变形在弹性范围内,煤体的变形方程可表示为
| $ G\sum\limits_{j = 1}^3 {\frac{{{\partial ^2}{u_i}}}{{\partial x_j^2}} + \frac{G}{{1-2\nu }}\sum\limits_{j = 1}^3 {\frac{{{\partial ^2}{u_j}}}{{\partial {x_j}\partial {x_i}}}-\frac{{\left( {3\lambda-2G} \right)}}{{3{k_{\text{s}}}}}\frac{{\partial p}}{{\partial {x_i}}} + \left( {\frac{{\sigma \left( {1 - \varphi } \right)}}{p} + \varphi } \right)\frac{{\partial p}}{{\partial {x_i}}} + {F_i} = 0} }, $ | (5) |
式中:G、λ为Lame常数;u为煤体位移,m;ν为煤体泊松比;Fi为煤体体积力分量;σ为总应力,MPa。
3.4 瓦斯渗流Klikenberg效应在煤体微孔结构中,瓦斯在煤体中的渗流需考虑Klikenberg效应,瓦斯渗流速度vf为与其动力粘度μ、压力梯度∇p的关系为[27]
| $ {v_{\text{f}}} =-k\left( {1 + c/p} \right)\nabla p/\mu, $ | (6) |
式中c为Klikenberg系数,MPa。
3.5 连续性方程在煤层瓦斯渗流过程中,质量不变,因而流动满足连续性方程
| $ \nabla \cdot \left( {{\rho _{\text{f}}}{v_{\text{f}}}} \right) + \partial Q/\partial t = 0。$ | (7) |
结合式(2)~(4)、式(6)和式(7),整理后可得煤层瓦斯渗流场方程28-29]
| $ \left[{\frac{{abf{p_0}}}{{{{\left( {1 + bp} \right)}^2}}} + \varphi + \frac{{p\left( {1-\varphi } \right)}}{{{k_{\text{s}}}}}} \right]\frac{{\partial p}}{{\partial t}} - \frac{1}{2}\nabla \cdot \left[{\frac{k}{\mu }\left( {1 + \frac{c}{p}} \right)\nabla p} \right] + p\alpha \frac{{\partial {\varepsilon _{\text{v}}}}}{{\partial t}} = 0, $ | (8) |
式中:
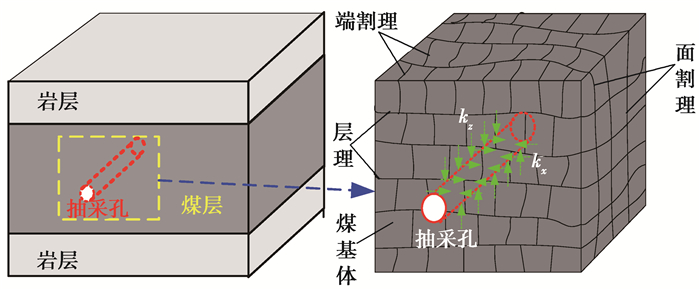
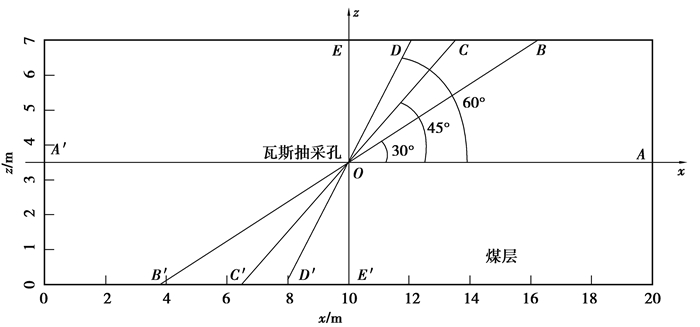
为了与现场测试对比,抽采孔如图 6所示,平行层理且沿端割理方向。瓦斯抽采模型几何尺寸为沿煤层走向取20 m(煤层厚度取7 m),抽采孔直径94 mm。上覆岩层应力9.6 MPa,考虑地质异常(有地质构造),侧压系数取1(即侧向压力为9.6 MPa)。在模型图 7中OA,OB,OC,OD,OE与x方向夹角分别为0°,30°,45°,60°和90°,以分析抽采过程中瓦斯压力与有效抽采距离的关系(抽采负压30 kPa)。
|
图 6 不同钻孔方位瓦斯抽采渗流示意图 Figure 6 Diagram of borehole planing and gas seepage |
|
图 7 瓦斯抽采几何模型的示意图 Figure 7 Schematic diagram of geometric model of gas drainage |
由式(3)~(5)和式(8)组成煤层瓦斯渗流的耦合模型,其求解初边值条件为:
1) 初始条件
p|t=0=p0;σ|t=0=0;
u|t=0=ui;∂u/∂xi|t=0=vi。
2)边界条件
压力:p|t=0=p0;
位移:u|bouudary=ui;
荷载:σij·nj|boundary=σ0。
4.3 参数选取焦作九里山矿二1煤层的原始瓦斯压力为1.21 MPa,根据煤样渗透率与瓦斯压力的变化规律,即式(1),计算可得此压力下原始煤层渗透率kx0=1.645×10-16m2和kz0=0.628 7×10-16 m2,煤体的物理参数和瓦斯抽采参数如表 2所示。
| 表 2 瓦斯抽采参数 Table 2 Drainage parameters used in calculation on coal mine |
煤层瓦斯流动的根源在于瓦斯压力梯度和抽采负压,在瓦斯抽采过程中,抽采钻孔周围煤层中的瓦斯压力不断降低,以瓦斯压力0.74 MPa为基准,形成一个以抽采孔为中心的类圆形影响区,即有效抽采区域[30]。
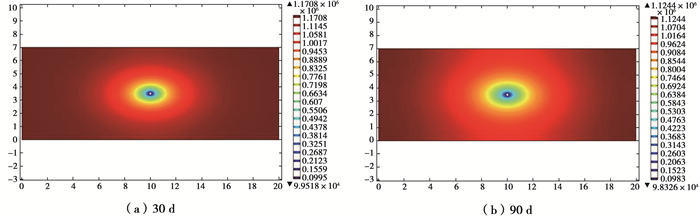
在抽采负压30 kPa下,可以数值模拟不同预抽时间内煤层瓦斯压力,如图 8所示。总的来说,煤层瓦斯压力与预抽时间正相关,即预抽时间时间越长,瓦斯压力降低的区域越大。在煤体内瓦斯渗透率各向异性,进而煤层瓦斯压力等值线是类椭圆形态。且渗透率越大,该方向瓦斯压力降低越快。
|
图 8 抽采过程瓦斯压力分布形态 Figure 8 Distribution of gas pressure in extraction process |
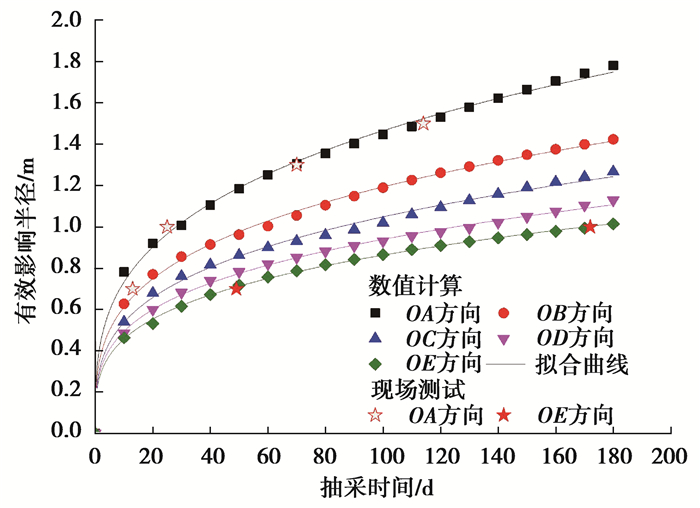
从图 9可以看出,相同预抽时间内不同方向上煤层瓦斯压力变化有一定的差别,特别是距离抽采孔越近,差别越明显。而且,随着预抽时间增加,煤层瓦斯压力降低越加显著。不同方向煤层瓦斯有效抽采半径随预抽时间的变化规律如图 10所示,任一方向上有效抽采半径与抽采时间的关系都满足幂指数形式,可用式(9)表示,拟合参数如表 3所示,相关系数均达到0.99以上。而且,数值模拟结果无论从变化规律,还是定量比较,均与实测结果一致。即数值模拟结果切实可行。
| $ r = \alpha {t^\beta }。$ | (9) |
|
图 9 瓦斯压力径向变化规律 Figure 9 Gas pressure change rules along radial direction |
|
图 10 有效抽采半径随抽采时间变化规律 Figure 10 Laws of effective extraction radius with drainage time |
| 表 3 不同方向有效抽采半径拟合参数(30 kPa) Table 3 Fitting parameters of effective drainage radius in differeat directions(30 kPa) |
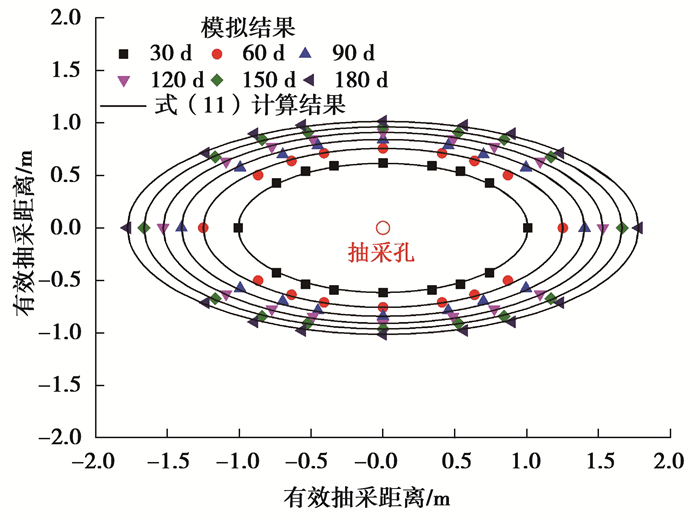
在图 7中,所建立的模型区域以A′A和E′E线轴对称,且以抽采孔O中心对称。由此,可得不同预抽时间内煤层有效抽采区域如图 11所示。
|
图 11 有效抽采区域(30 kPa) Figure 11 Effective drainage areas(30 kPa) |
从图 11可知,各向渗透异性煤层瓦斯抽采过程中有效抽采半径是以抽采孔为中心的类似椭圆形。为了证明有效抽采区域为椭圆,作如下计算分析:设预抽时间为t,渗透率大的方向(平行层理方向)有效抽采距离rlt为椭圆长轴,渗透率小的方向(垂直层理方向)有效抽采距离rst为椭圆短轴,以抽采孔为中心的有效抽采区域方程为:
| $ {x^2}/{r_{{\text{lt}}}}^2 + {z^2}/{r_{{\text{st}}}}^2 = 1 $ | (10) |
在不同预抽时间内,选取rlt和rst,并采用式(10)进行计算并绘制图形(图 11中),从图 11可以看出,相同预抽时间,式(10)计算得到的椭圆与不同方向有效抽采距离完全一致,从而表明了各向异性煤层瓦斯抽采有效区域是以抽采孔为中心的椭圆(长轴为最大有效距离,短轴为最小有效距离)。
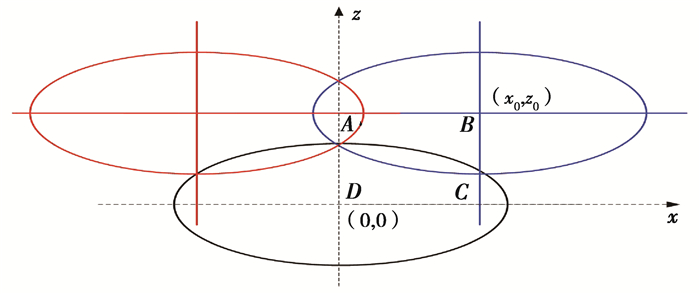
6.2 钻孔间距及合理布孔计算分析假设某一预抽孔坐标为(0,0),并沿抽采有效距离的长轴rlt、短轴rst方向建立直角坐标x,z,如图 12所示。若与之相邻的另一预抽孔坐标为(x0,z0),则基于煤层瓦斯抽采不仅要消除空白带,还要遵循抽采孔数目最少的原则,则合理布孔方式需满足ABCD区域面积最大,即x0z0最大。
|
图 12 合理布孔方式示意图 Figure 12 Schematic diagram of reasonable layout of boreholes |
此时,(x-x0)2/rlt2+(z-z0)2/rst2=1过(0,rst)点,且0 < x0 < rlt, rst < z0 < 2rst,即:
| $ {x_0}^2/{r_{{\text{lt}}}}^2 + {\left( {{r_{{\text{st}}}}-{z_0}} \right)^2}/{r_{{\text{st}}}}^2 = 1。$ | (11) |
当ABCD区域面积最大时(x0z0最大),(x0z0)2也应最大,则
| $ \begin{gathered} {\left( {{x_0}{z_0}} \right)^2} = {r_{{\text{lt}}}}^2\left[{1-{{\left( {{r_{{\text{st}}}}-{z_0}} \right)}^2}/{r_{{\text{st}}}}^2} \right]{z_0}^2 = \hfill \\ \left( {{r_{{\text{lt}}}}^2/{r_{{\text{st}}}}^2} \right)\left[{{r_{{\text{st}}}}^2-{{\left( {{r_{{\text{st}}}}-{z_0}} \right)}^2}} \right]z_0^2 \leqslant \hfill \\ \left( {{r_{{\text{lt}}}}^2/{r_{{\text{st}}}}^2} \right) \cdot 0.5\left[{{{\left( {2{r_{{\text{st}}}}-{z_0}} \right)}^2} + {{\left( {{z_0}^3} \right)}^2}} \right]。\hfill \\ \end{gathered} $ | (12) |
当式(12)取等号时,即(2rst-z0)=z03时,(x0z0)2最大,即:
| $ {z_0}^3 + {z_0}-2{r_{{\text{st}}}} = 0。$ | (13) |
式(13)为典型卡尔丹公式,对其求解。
| $ \Delta = {r_{{\text{st}}}}^2 + {\left( {1/3} \right)^3}, $ |
| $ {Y_1} = {r_{{\text{st}}}} + \sqrt \Delta, {Y_2} = {r_{{\text{st}}}}-\sqrt \Delta 。$ |
可得z0满足条件的实数解为:
| $ {z_0} = \sqrt[3]{{{Y_1}}} + \sqrt[3]{{{Y_2}}}。$ | (14) |
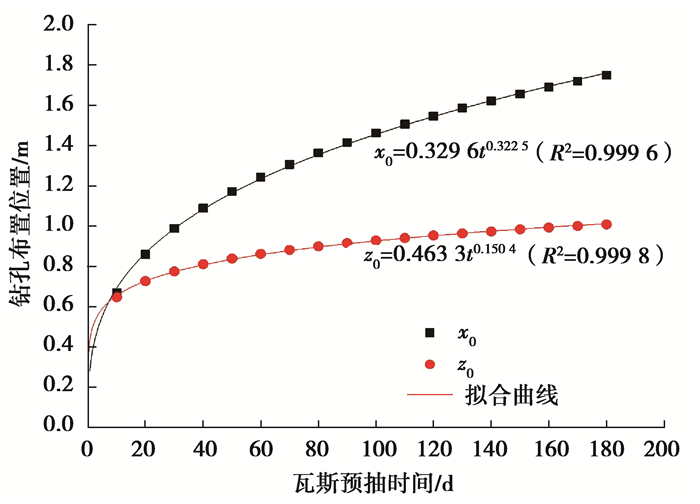
对于任一抽采时间t时,x、z方向上的有效抽采半径为rlt、rst,带入(14)和式(11)可求得布孔位置坐标(x0,z0),x0,z0分别与预抽时间t关系如图 13所示,可用函数式(15)表示。从图 13可以看出,在不同预抽时间下,钻孔布置间距随预抽时间的增大而增大,其中,平行层理方向布置间距增大较快,而垂直层理方向布置间距缓慢增大。
|
图 13 瓦斯预抽时间与钻孔布置位置关系(30 kPa) Figure 13 Relationship between gas pre-extraction time and boreholes arrangement(30 kPa) |
| $ \left\{ \begin{gathered} {x_0} = 0.329\;6{t^{0.322\;5}}\;\;\;\;\;\;\;\;\;\;\left( {{R^2} = 0.999\;6} \right), \\ {z_0} = 0.463\;3{t^{0.150\;4}}\;\;\;\;\;\;\;\;\;\;\;\left( {{R^2} = 0.999\;8} \right)。\\ \end{gathered} \right. $ | (15) |
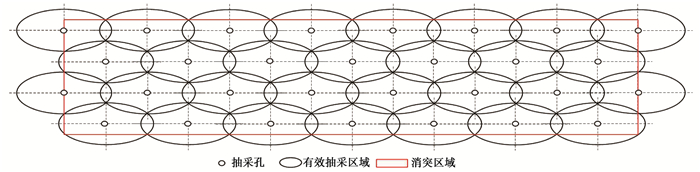
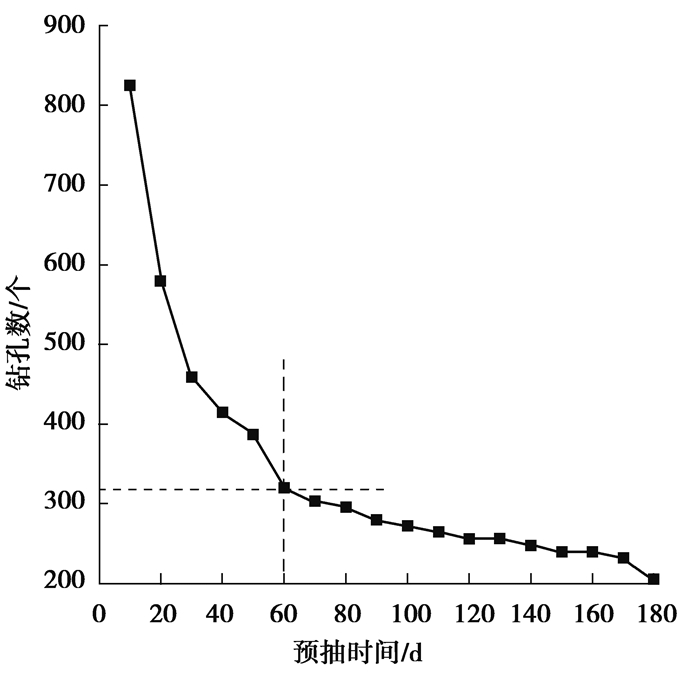
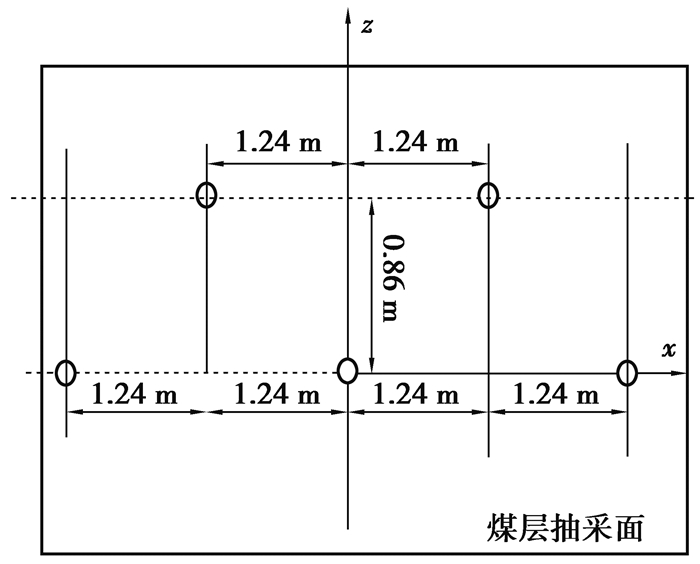
当确定了煤层预抽时间,采用式(15)分别计算出x0,z0,即可按照图 12对煤层抽采钻孔进行合理有效的布孔。在此,选取九里山矿一个7 m×100 m煤层抽采面(煤层厚度7 m,长度为100 m)来计算煤层瓦斯抽采钻孔合理布置(图 14为某一局部煤面抽采孔布置示意图)。如前所述,为了消除煤层突出危险性,瓦斯有效抽采区域应完全覆盖煤层,不留抽采空白带。在7 m×100 m煤层抽采面上,总抽采钻孔数与预抽时间的关系如图 15所示(抽采负压30 kPa),抽采钻孔数随预抽时间的增加先是迅速减小,而后缓慢减少至基本趋于定值。如当预抽时间为10 d,为消除突出危险性,百米需要825个抽采钻孔;预抽时间90 d,需要280个抽采钻孔;预抽时间120 d,需要256个抽采钻孔;而预抽时间150 d,需要240个抽采钻孔。因此,如果提前规划煤层抽采区的钻孔布置,可通过设计预抽时间和减少抽采钻孔数量来降低煤层瓦斯抽采成本。还可以看出,当百米抽采钻孔数量小于300,增加预抽时间不是非常有利于提高抽采效率。图 15因此成为权衡区域煤层瓦斯抽采钻孔数和预抽时间的基本参量,对于九里山矿煤层抽采面,预抽时间为60 d,煤层百米抽采钻孔(煤厚7 m)钻孔数320个为佳,其钻孔布置方式如图 16所示。
|
图 14 瓦斯抽采区域局部煤面钻孔布置示意图 Figure 14 Representative borehole arrangement |
|
图 15 百米煤层抽采钻孔数与预抽时间的关系(30 kPa) Figure 15 Relationship between pre-extraction time and borehole number(30 kPa) |
|
图 16 煤层抽采面合理布孔方式 Figure 16 Reasonable hole layout mode of coal seam |
煤层钻孔有效抽采半径的确定不仅有助于钻孔的合理布置,而且能够降低抽采成本。笔者首先在焦作九里山煤矿各向渗透异性煤层中进行了180 d瓦斯抽采有效半径的测试,并测试了各向异性煤样瓦斯渗透率,同时,建立煤层瓦斯抽采的耦合模型,数值分析各向渗透异性煤层的有效抽采距离。在现场测量和模拟结果的基础上,确定了各向异性煤层瓦斯抽采钻孔的有效影响面积,并设计了不同预抽时间下的钻孔布置。研究结果表明:
1) 煤体平行层理方向渗透率是垂直层理方向渗透率的2.6倍左右,进而导致瓦斯在煤层中各向渗透差异。
2) 在煤层瓦斯抽采过程中,各个方向上有效抽采半径均随预抽时间呈幂指数增大。而且渗透率越大,该方向有效抽采距离越大。
3) 各向渗透异性煤层瓦斯抽采过程中,有效抽采区域是以抽采孔为中心,最大有效抽采距离(平行层理方向)为长轴,最小有效抽采距离(垂直层理方向)为短轴的椭圆。
各向异性煤层中,有效抽采区域是以抽采孔为中心,平行层理方向的有效抽采距离为长轴,垂直层理方向有效抽采距离为短轴的椭圆。
4) 九里山煤矿在7 m×100 m煤层抽采面总抽采钻孔数随预抽时间增加先是迅速减小,而后缓慢减少至基本趋于定值。当百米抽采钻孔数量小于300时,增加预抽时间对抽采效率的提高影响不明显。
| [1] |
申宝宏, 刘见中, 张泓.
我国煤矿瓦斯治理的技术对策[J]. 煤炭学报, 2007, 32(7): 673–679.
SHEN Baohong, LIU Jianzhong, ZHANG Hong. The technical measures of gas control in China coal mines[J]. Journal of China Coal Society, 2007, 32(7): 673–679. (in Chinese) |
| [2] |
程远平, 俞启香, 周红星, 等.
煤矿瓦斯治理"先抽后采"的实践与作用[J]. 采矿与安全工程学报, 2006, 23(4): 389–392.
CHENG Yuanping, YU Qixiang, ZHOU Hongxing, et al. Practice and effectiveness of "draining gas before coal mining" to prevent gas from bursting[J]. Journal of Mining & Safety Engineering, 2006, 23(4): 389–392. (in Chinese) |
| [3] |
刘军, 王兆丰, 李学臣, 等.
消除矿井瓦斯抽采空白带方法的研究[J]. 煤炭科学技术, 2012, 40(12): 59–61.
LIU Jun, WANG Zhaofeng, LI Xuechen, et al. Study on the methods of eliminating blank zone of mine gas drainage[J]. Coal Science and Technology, 2012, 40(12): 59–61. (in Chinese) |
| [4] |
王伟有, 汪虎.
基于COMSOL的瓦斯抽采有效半径数值模拟[J]. 矿业工程研究, 2012, 27(2): 40–43.
WANG Weiyou, WANG Hu. Research on the gas extraction effective radius by simulation based on COMSOL multiphysics[J]. Mineral Engineering Research, 2012, 27(2): 40–43. (in Chinese) |
| [5] | Li H Y, Shimada S, Zhang M. Anisotropy of gas permeability associated with cleat pattern in a coal seam of the Kushiiro coalfield in Japan[J]. Environmental Geology, 2004, 47(1): 45–50. DOI:10.1007/s00254-004-1125-x |
| [6] |
黄学满.
煤结构异性对瓦斯渗透特性影响的实验研究[J]. 矿业安全与环保, 2012, 39(2): 1–3.
HUANG Xueman. Experimental study on influence of structural anisotropy of coal upon gas permeability[J]. Mining Safety & Environmental Protection, 2012, 39(2): 1–3. (in Chinese) |
| [7] |
潘荣锟, 程远平, 董骏, 等.
不同加卸载下层理裂隙煤体的渗透特性研究[J]. 煤炭学报, 2014, 39(3): 473–477.
PAN Rongkun, CHENG Yuanping, DONG Jun, et al. Research on permeability characteristics of layered natural coal under different loading and unloading[J]. Journal of China Coal society, 2014, 39(3): 473–477. (in Chinese) |
| [8] | Laubach S E, Marrett R A, Olson J E, et al. Characteristics and origins of coal cleat:A review[J]. International Journal of Coal Geology, 1998, 35(1/2/3/4): 175–207. |
| [9] |
陈金刚, 秦勇, 宋全友, 等.
割理方向与煤层气抽放效果的关系及预测模型[J]. 中国矿业大学学报, 2003, 32(3): 223–226.
CHEN Jingang, QIN Yong, SONG Quanyou, et al. Coupling relationship between direction of coalbed cleat and methane drainage effect and its prediction model[J]. Journal of China University of Mining & Technology, 2003, 32(3): 223–226. (in Chinese) |
| [10] |
傅雪海, 秦勇, 姜波, 等.
煤割理压缩实验及渗透率数值模拟[J]. 煤炭学报, 2001, 26(6): 573–577.
FU Xuehai, QIN Yong, JIANG Bo, et al. Compress experiment of coal cleat and mathematical simulation of coal reservoir permeability[J]. Journal of China Coal Society, 2001, 26(6): 573–577. (in Chinese) |
| [11] |
刘洪林, 王红岩, 张建博.
煤储层割理评价方法[J]. 天然气工业, 2000, 20(4): 27–29.
LIU Honglin, WANG Hongyan, ZHANG Jianbo. Evaluation method of cleats in coal reservoir bed[J]. Natural Gas Industry, 2000, 20(4): 27–29. (in Chinese) |
| [12] | Koenig P A, Stubbs P B. Interference testing of a coal-bed methane reservoir[C]//SPE Unconventional Gas Technology Symposium, May 18-21, 1986, Louisville, Kentucky. [S. l. ]: Society of Petroleum Engineers, 1986. |
| [13] | WANG S G, Elsworth D, Liu J S. Permeability evolution in fractured coal:The roles of fracture geometry and water-content[J]. International Journal of Coal Geology, 2011, 87(1): 13–25. DOI:10.1016/j.coal.2011.04.009 |
| [14] | Lin H F, Huang M, Li S G, et al. Numerical simulation of influence of Langmuir adsorption constant on gas drainage radius of drilling in coal seam[J]. International Journal of Mining Science and Technology, 2016, 26(3): 377–382. DOI:10.1016/j.ijmst.2016.02.002 |
| [15] |
王宏图, 江记记, 王再清, 等.
本煤层单一顺层瓦斯抽采钻孔的渗流场数值模拟[J]. 重庆大学学报, 2011, 34(4): 24–29.
WANG Hongtu, JIANG Jiji, WANG Zaiqing, et al. Numerical simulation of seepage field of gas extraction drilling of single bedding of mining-coal bed[J]. Journal of Chongqing University, 2011, 34(4): 24–29. DOI:10.11835/j.issn.1000-582X.2011.04.005 (in Chinese) |
| [16] |
梁冰, 袁欣鹏, 孙维吉.
本煤层顺层瓦斯抽采渗流耦合模型及应用[J]. 中国矿业大学学报, 2014, 43(2): 208–213.
LIANG Bing, YUAN Xinpeng, SUN Weiji. Seepage coupling model of in-seam gas extraction and its applications[J]. Journal of China University of Mining & Technology, 2014, 43(2): 208–213. (in Chinese) |
| [17] |
尹光志, 李铭辉, 李生舟, 等.
基于含瓦斯煤岩固气耦合模型的钻孔抽采瓦斯三维数值模拟[J]. 煤炭学报, 2013, 38(4): 535–541.
YIN Guangzhi, LI Minghui, LI Shengzhou, et al. 3D numerical simulation of gas drainage from boreholes based on solid-gas coupling model of coal containing gas[J]. Journal of China Coal Society, 2013, 38(4): 535–541. (in Chinese) |
| [18] |
鲁义, 申宏敏, 秦波涛, 等.
顺层钻孔瓦斯抽采半径及布孔间距研究[J]. 采矿与安全工程学报, 2015, 32(1): 156–156.
LU Yi, SHEN Hongmin, QIN Botao, et al. Gas drainage radius and borehole distance along seam[J]. Journal of Mining & Safety Engineering, 2015, 32(1): 156–156. (in Chinese) |
| [19] |
季淮君, 李增华, 杨永良, 等.
基于瓦斯流场的抽采半径确定方法[J]. 采矿与安全工程学报, 2013, 30(6): 917–921.
JI Huaijun, LI Zenghua, YANG Yongliang, et al. Drainage radius measurement based on gas flow field[J]. Journal of Mining & Safety Engineering, 2013, 30(6): 917–921. (in Chinese) |
| [20] |
余陶, 卢平, 孙金华, 等.
基于钻孔瓦斯流量和压力测定有效抽采半径[J]. 采矿与安全工程学报, 2012, 29(4): 596–600.
YU Tao, LU Ping, SUN Jinhua, et al. Measurement of effective drainage radius based on gas flow and pressure of boreholes[J]. Journal of Mining & Safety Engineering, 2012, 29(4): 596–600. (in Chinese) |
| [21] |
岳高伟, 王宾宾, 曹汉生, 等.
结构异性煤层顺层钻孔方位对有效抽采半径的影响[J]. 煤炭学报, 2017, 42(Suppl1): 138–147.
YUE Gaowei, WANG Binbin, CAO Hansheng, et al. Influence of effective drainage radius by borehole orientation along seam with anisotropic permeability[J]. Journal of China Coal Society, 2017, 42(Suppl1): 138–147. (in Chinese) |
| [22] |
魏国营, 秦宾宾.
煤体钻孔瓦斯有效抽采半径判定技术[J]. 辽宁工程技术大学学报(自然科学版), 2013, 32(6): 754–758.
WEI Guoying, QIN Binbin. Technology for determining effective drainage radius of coal seam drill hole[J]. Journal of Liaoning Technical University(Natural Science), 2013, 32(6): 754–758. (in Chinese) |
| [23] |
岳高伟, 王辉, 赵宇, 等.
结构异性煤体渗透率特性[J]. 科技导报, 2015, 33(12): 50–55.
YUE Gaowei, WANG Hui, ZHAO Yu, et al. Permeability characteristics of structurally anisotropic coal[J]. Science & Technology Review, 2015, 33(12): 50–55. (in Chinese) |
| [24] |
魏建平, 李明助, 王登科, 等.
煤样渗透率围压敏感性试验研究[J]. 煤炭科学技术, 2014, 42(6): 76–80.
WEI Jianping, LI Mingzhu, WANG Dengke, et al. Experimental research on sensibility of coal samples permeability under confining pressure[J]. Coal Science and Technology, 2014, 42(6): 76–80. (in Chinese) |
| [25] |
王猛. 本煤层钻孔抽采防突效果影响因素研究[D]. 焦作: 河南理工大学, 2015. WANG Meng. Influential factors research on the drilling extraction of outburst prevention effects in the coal seam[D]. Jiaozuo: Henan Polytechnic University, 2015. (in Chinese) |
| [26] |
赵继展, 韩保山, 陈志胜, 等.
煤层瓦斯含量计算方法探讨[J]. 中国煤田地质, 2006, 18(5): 22–24.
ZHAO Jizhan, HAN Baoshan, CHEN Zhisheng, et al. Discussion on coal bed methane content estimation method[J]. Coal Geology of China, 2006, 18(5): 22–24. (in Chinese) |
| [27] | Klinkenberg L J. The permeability of porous media to liquids and gases[C]//Drilling and Production Practice, January 1, 1941, New York. New York: American Petroleum Institute, 1941: 200-213. |
| [28] | Saghafi A, Faiz M, Roberts D. CO2 storage and gas diffusivity properties of coals from Sydney Basin, Australia[J]. International Journal of Coal Geology, 2007, 70(1/2/3): 240–254. |
| [29] | Hu G Z, Wang H T, Fan X G, et al. Mathematical model of coalbed gas flow with Klinkenberg effects in multi-physical fields and its analytic solution[J]. Transport in Porous Media, 2009, 76(3): 407–420. DOI:10.1007/s11242-008-9254-4 |
| [30] | Wu D M, Wang H F, Ge C G, et al. Research on forced gas draining from coal seams by surface well drilling[J]. Mining Science and Technology, 2011, 21(2): 229–232. |
 2018, Vol. 41
2018, Vol. 41

