行星滚柱丝杠(PRS, planetary roller screw)作为精密动力传动机构,综合了行星轮系、滚珠丝杠和滚针轴承的运动特点,可实现旋转运动与直线运动的相互转换。PRS具有刚度大、承载能力高、结构紧凑、导程可设计、传动平稳、寿命长等优点,逐步作为直线驱动组件或执行机构应用于航空工业、数控机床及机器人等领域[1]。
近年来,众多学者在啮合理论、运动学分析、优化设计及试验研究等方面对PRS进行了深入的研究。Hojjat等[2]从行星滚柱丝杠整体出发,开展了滚柱与丝杠间轴向位移方面的研究,探究了传动过程中丝杠与滚柱产生轴向滑动的原因。Velinsky [3],Matthew[4],Jones [5]等从运动学角度出发,建立PRS运动学模型,开展了行星滚柱丝杠的位置分析、变形分析、效率及承载能力分析;Aurégan等[6]在建立有限元模型的基础上,开展了行星滚柱丝杠副接触点的研究;Matthew等[7]将PRS等效成弹簧系统,并在此基础上对行星滚柱丝杠的刚度及承载能力开展了研究;Tong[8],付晓军[9],马尚君[10-11]等在建立PRS摩擦力矩计算模型及有限元模型的基础上,开展了行星滚柱丝杠动态特性、传动性能、螺旋曲面啮合副、摩擦热等方面的研究;李凯等[12]开展了行星滚柱丝杠副传动特性方面的研究。
上述研究表明,不同的模型会影响到对于相关传动性能的分析,要建立合理有效的PRS模型,首先应从机构学原理上对PRS进行运动学分析,而机构自由度作为确定机构或运动链位形的独立参数,在实际工程应用中具有重要的意义。
目前关于PRS自由度计算的研究多以滚珠丝杠作为参考,分析过程中将滚柱等效成类似滚珠的球体,这无法充分反映螺旋副的接触及运动特性。
笔者基于空间螺旋理论开展行星滚柱丝杠副机构学分析,综合考虑行星滚柱丝杠副空间机构特点,建立了PRS机构运动简图,分析了系统各构件的运动特性,计算出不同数量构件条件下的机构自由度,通过对比单滚柱、单挡圈机构自由度,证明了基于空间螺旋理论对PRS自由度计算的合理性和有效性,一定程度上揭示行星滚柱丝杠副运动学原理。
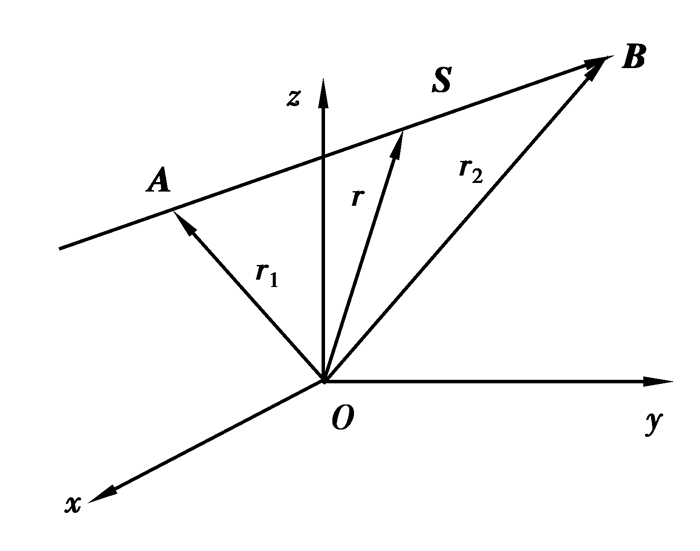
1 螺旋理论基础 1.1 螺旋基本概念空间直线AB,如图 1,该直线可以由方向矢量S和位置相关矢量S0来共同表示[15],也叫做线矢或节距为零的螺旋,其表达式为
| $ \mathit{\pmb{$}} = (\mathit{\boldsymbol{S}};{\mathit{\boldsymbol{S}}_0}) = \left( {\mathit{\boldsymbol{S}};\mathit{\boldsymbol{r}} \times \mathit{\boldsymbol{S}}} \right) = \left( {l\;m\;n;p\;q\;r} \right), $ | (1) |
|
图 1 空间直线 Figure 1 Space straight line |
式中,(S; S0)为直线的Plücker坐标,有6个分量,即(l m n; p q r)。
在应用中,用h=S·S0/(S·S)表示螺旋的节距,S0=r×S+hS0。当节距为零时就是线矢,表示转动副或者约束力,而节距无穷大时,即$=(0;S),S表示方向适量,该螺旋表示移动副或者约束力偶。
1.2 螺旋的互逆性对于2个螺旋$=(S;S0),$r=(Sr;S0r),他们的互易积[16]记为
| $ \mathit{\pmb{$}}^\circ {\mathit{\pmb{$}}^r} = \mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{S}}_0^r + {\mathit{\pmb{$}}^r} \cdot {\mathit{\boldsymbol{S}}_0} $ | (2) |
运动螺旋和力螺旋的互易积就是这2个螺旋产生的瞬时功率。
若2个螺旋的互易积为零,则它们互逆或互为反螺旋。即当$与$r互为反螺旋时,$°$r=0。对于运动螺旋$的反螺旋$r,如果它的节距h为零,则代表 1个约束力,限制了其沿约束力方向的移动;如果它的节距h为无穷大,则代表 1个约束力偶,限制了其绕此力偶方向的转动。
1.3 修正G-K公式机构自由度的计算可以用所有运动构件总自由度减去所有约束数的差表示。对于单环机构,可以采用上述计算方式;对于多环机构,除应考虑多环形成时出现的过约束(即冗余约束),还应考虑可能产生的局部自由度。
经过多年的研究发展,对于自由度的求解方法日臻成熟,其中,应用G-K公式已成功解决诸多疑难机构的自由度[13-14]。
修正的G-K公式为
| $ M = d\left( {n - g - 1} \right) + \sum\limits_{i = 1}^g {{f_i} + \nu - \zeta , } $ | (3) |
式中:M为机构自由度;d为机构的阶数;n为含机架在内的构件数;g为运动副数;fi为第i个运动副的自由度;ν为冗余约束的数目;ζ为局部自由度。其中,d=6-λ,λ为机构的公共约束数。
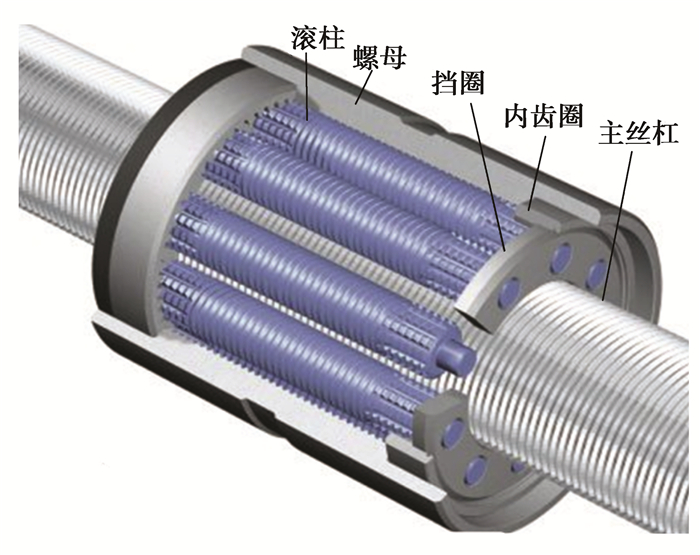
2 标准行星滚柱丝杠副工作原理PRS的结构组成如图 2所示,主要由主丝杠、滚柱、螺母、内齿圈、挡圈等构件组成。PRS工作原理与行星齿轮结构类似,即电机带动旋转的主丝杠,主丝杠与滚柱通过螺旋副啮合,滚柱与螺母也通过螺旋副啮合,利用摩擦转矩驱动将主丝杠的旋转运动转化为螺母的直线运动。其中,主丝杠作为驱动结构,与环绕在其周围的滚柱螺纹旋合,滚柱在沿螺纹轨道前行的同时通过两端直齿与安装在螺母上的内齿圈啮合,不但保证滚柱围绕丝杠公转的同时实现自转,而且保证滚柱与丝杠轴线平行;螺母周向固定,在滚柱作用下做直线运动;在安装的过程中,为保证滚柱间相对位置,通过两端挡圈支撑来保证其相对位置,同时保持与螺母的轴向相对静止。
|
图 2 行星滚柱丝杠 Figure 2 Planetary roller screw |
文中基于PRS的空间机构特点及运动特性,给出图 3所示机构运动简图。

|
图 3 行星滚柱丝杠副机构简图 Figure 3 Planetary roller screw mechanism schematic diagram 注:1.螺母;2.滚柱;3.主丝杠;4.挡圈 |
主丝杠类似太阳轮,滚柱视为行星轮,螺母视为内齿轮,挡圈视为行星架。当主丝杠旋转且螺母的周向固定时,滚柱在圆周方向做类似行星运动,运动过程中通过螺旋副将主丝杠的转动转化为螺母的直线运动,运动过程中挡圈起到了行星轮系中行星架的作用。
3.2 行星滚柱丝杠副自由度计算当机构所有的运动副均以运动螺旋$m表示,它们构成一个螺旋系A,若存在一个与螺旋系A中每个螺旋$m均相逆的反螺旋$r,这个反螺旋就是该机构的一个公共约束,它反映了机械结构对运动部分的约束,反螺旋的数目就是公共约束数目。
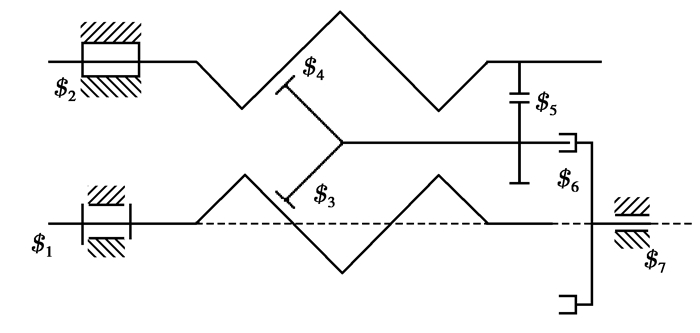
3.2.1 单滚柱、单挡圈条件下PRS分析当PRS构件只包含基础构件主丝杠、单个滚柱、单个挡圈时,其机构运动简图如图 4所示。考虑运动螺旋系的Plücker坐标,选定主丝杠轴为坐标系Z轴,找出其中运动螺旋。
|
图 4 行星滚柱丝杠副机构简图1 Figure 4 Planetary roller screw mechanism schematic diagram1 |
该机构可以简化为7个运动副,Plücker坐标分别为:
丝杠—机架转动副:$1:(0 0 1;0 0 c1),
螺母—机架移动副:$2:(0 0 1;0 0 c2),
丝杠—滚柱螺旋副:$3:(0 0 1;0 0 c3),
滚柱—螺母螺旋副:$4:(0 0 1;a4 b4 c4),
滚柱—内齿圈齿轮副:$5:(0 0 1;a5 b5 c5),
滚柱—挡圈转动副:$6:(0 0 1;a6 b6 c6),
挡圈—机架圆柱副:$7:(0 0 1;0 0 c7),
其中:ai和bi为不同的实数,并且在机构运行过程中ai和bi的数值发生变化;ci为相同的实数,即丝杠、滚柱、螺母3者节距h相等。
由于7个运动螺旋的Plücker坐标中的第1、第2个元素恒为零,与位形变化无关;丝杠、滚柱、螺母三者节距h相等,利用观察法,螺旋系A的公共反螺旋有3个:$11r:(0 0 0;1 0 0),$12r:(0 0 0;0 1 0),$13r:(0 0 1;0 0 -c)。
机构运动螺旋系有3个反螺旋,即机构有3个公共约束,λ=3,机构的阶数为d=6-λ=3。
对于机构中的冗余自由度,可以看出滚柱与内齿圈齿轮副属于虚约束多余自由度,即机构冗余自由度ν=1,局部自由度ζ=0。无论机构在何种位形下其反螺旋,即公共约束不发生变化,并且其冗余约束也不发生变化,所以自由度不是瞬时的,是连续的。
行星滚柱丝杠机构的自由度为
| $ \begin{gathered} M = d\left( {n - g - 1} \right) + \sum\limits_{i = 1}^g {{f_i} + \nu - \zeta = } \hfill \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3 \times \left( {5 - 7 - 1} \right) + \left( {1 \times 5 + 2 \times 2} \right) + 1 - 0 = 1 \hfill 。\\ \end{gathered} $ | (4) |
从式(4)计算结果可以看出,单滚柱、单挡圈条件下的行星滚柱丝杠副自由度为1,此时只要给主丝杠一旋转运动,螺母将产生确定的直线运动,即行星滚柱丝杠副将主丝杠的旋转运动转化为螺母的直线运动。
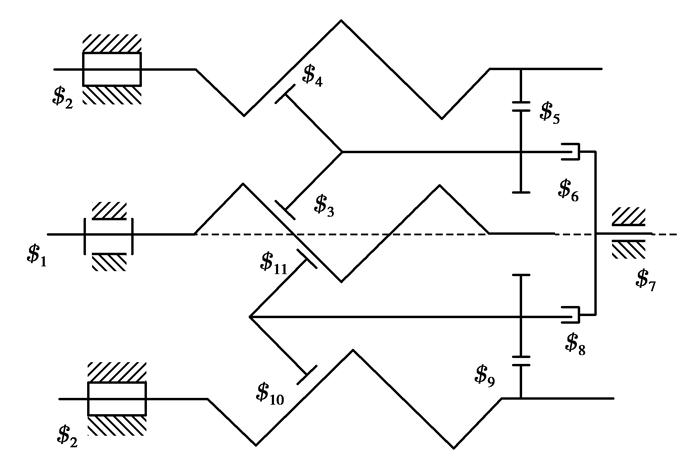
3.2.2 双滚柱、单挡圈条件下PRS分析当PRS构件在单滚柱、单螺母的基础上增加1个滚柱时,机构运动简图如图 5所示,相当于增加1个构件、4个运动副,对整个系统来说公共约束不发生变化,即阶数不发生变化。此处增加的运动副均为冗余约束。
|
图 5 行星滚柱丝杠副机构简图2 Figure 5 Planetary roller screw mechanism schematic diagram2 |
机构自由度为
| $ \begin{gathered} M = d\left( {n - g - 1} \right) + \sum\limits_{i = 1}^g {{f_i} + \nu - \zeta = } {\text{ }} \hfill \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3 \times \left( {6 - 11 - 1} \right) + \left( {1 \times 8 + 2 \times 3} \right) + 5 - 0 = 1 \hfill。\\ \end{gathered} $ | (5) |
由式(5)计算结果,机构自由度仍为1。此时考虑滚柱数量对于机构自由度产生的影响,增加n个滚柱构件,对于整个系统并未改变原基本机构的运动学特性,因此, 可认为其所增加的运动副均为冗余约束。
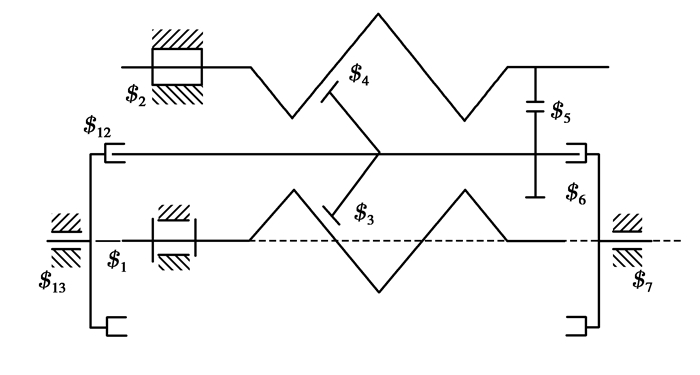
3.2.3 单滚柱、双挡圈条件下PRS分析当PRS构件在单滚柱、单螺母的基础上增加1个挡圈时,即左右各1个挡圈起保持架作用,机构运动简图如图 6所示,相当于增加1个构件、2个运动副,对于增加的构件挡圈,其力螺旋与单挡圈时的力螺旋线性相关,因此,对于系统的阶数不产生影响。
|
图 6 行星滚柱丝杠副机构简图3 Figure 6 Planetary roller screw mechanism schematic diagram3 |
机构自由度为
| $ \begin{gathered} M = d\left( {n - g - 1} \right) + \sum\limits_{i = 1}^g {{f_i} + \nu - \zeta = } {\text{ }} \hfill \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3 \times \left( {6 - 9 - 1} \right) + \left( {1 \times 6 + 2 \times 3} \right) + 1 - 0 = 1 \hfill。\\ \end{gathered} $ | (6) |
由式(6)计算结果可知,机构自由度仍为1。考虑挡圈的数量对于机构自由度产生的影响,对于整个系统来说,可以构想为类行星轮系,挡圈起到行星架作用,即在运动过程中,挡圈不仅起到保证滚柱间位置的作用,其本身也参与到机构的运动过程中,考虑所增加的运动副,挡圈运动螺旋与单挡圈时的螺旋系线性相关,即公共约束未发生变化,并未改变原基本机构的运动学特性,系统自由度不发生变化。
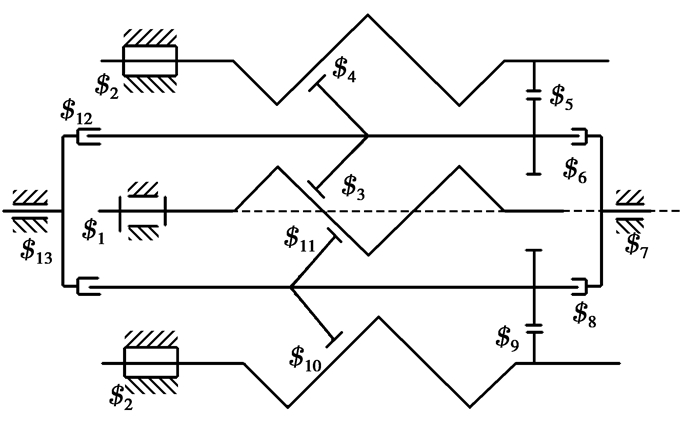
3.2.4 双滚柱、双挡圈条件下PRS分析当PRS构件在单滚柱、单螺母的基础上分别增加1个滚柱、1个挡圈时,机构运动简图如图 7所示。由上述分析可知,增加滚柱与挡圈的数量对于公共约束不产生影响,在计算机构自由度时只需找出运动副中所产生的冗余自由度。简化整个机构,可以认为系统含有6个运动构件、13个运动副,其中5个为虚约束。
|
图 7 行星滚柱丝杠副机构简图4 Figure 7 Planetary roller screw mechanism schematic diagram4 |
机构自由度为
| $ \begin{gathered} M = d\left( {n - g - 1} \right) + \sum\limits_{i = 1}^g {{f_i} + \nu - \zeta = } {\text{ }} \hfill \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3 \times \left( {7 - 13 - 1} \right) + \left( {1 \times 9 + 2 \times 4} \right) + 5 - 0 = 1 \hfill 。\\ \end{gathered} $ | (7) |
由式(7)计算结果,机构自由度仍为1。在计算PRS自由度过程中,相对于单滚柱、单挡圈条件下系统的自由度,增加滚柱与挡圈的数量对于系统自由度没有影响。由自由度概念可知,只要给定与机构自由度相同的独立运动参数,则机构中各构件具有确定的相对运动。在该行星滚柱丝杠副中,给定主丝杠一旋转运动,滚柱将做类行星运动,并通过螺旋副带动螺母做沿轴向的直线运动,此时,挡圈作为行星架在转动的同时,与滚柱保持轴向静止状态。
通过以上分析可以看出,基于螺旋理论的修正G-K公式是非常有效的。这一方法基于约束螺旋理论,给出合理的机构运动简图,选定坐标系,给出运动螺旋系的Plücker坐标,然后,求出反螺旋系,确定有效运动副数量。传统行星滚柱丝杠计算方法将空间机构简化成平面机构,区分高低副,未能在分析计算过程中反应出PRS作为空间螺旋机构的特点。利用基于螺旋理论的修正G-K公式计算,在不简化机构的前提下,通过分析计算过程直观地反应出行星滚柱丝杠副作为空间螺旋机构的运动学特性。
4 结论通过对PRS空间机构的分析,给出PRS运动机构简图,并基于螺旋理论的空间机构自由度,提出了PRS空间机构自由度计算方法。通过分析各运动副间的运动螺旋,求解螺旋系的反螺旋,确定系统的约束与过约束,简化了自由度计算流程。
分别计算了不同构件条件下PRS的自由度,通过计算验证了滚柱的数量对于系统自由度没有影响,增加的滚柱对于整个系统来说相当于虚约束,但增加滚柱又起到分载的作用,因此,滚柱数量应由其安装空间所决定,作为精密传动件,对于制造与安装精度有着较高的要求。
滚柱与安装在螺母上的内齿圈啮合,不仅保证滚柱围绕丝杠公转的同时自转,而且保证滚柱与丝杠轴线平行。利用滚柱两端的挡圈保证滚柱间相对位置,并且到类行星轮系中行星架作用。对后期PRS的设计与分析提供理论依据。
| [1] |
刘更, 马尚君, 佟瑞庭, 等.
行星滚柱丝杠副的新发展及关键技术[J]. 机械传动, 2012, 36(5): 103–108.
LIU Geng, MA Shangjun, TONG Ruiting, et al. New development and key technology of planetary roller screw[J]. Mechanism Transmission, 2012, 36(5): 103–108. (in Chinese) |
| [2] | Hojjat Y, Agheli M M. A comprehensive study on capabilities and limitations of roller-screw with emphasis on slip tendency[J]. Mechanism & Machine Theory, 2009, 44(10): 1887–1899. |
| [3] | Velinsky S A, Chu B, Lasky T A. Kinematics and efficiency analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Design, 2009, 131(1): 1–8. |
| [4] | Matthew H J, Velinsky S A, Lasky T A. Contact iinematics in the roller screw mechanism[J]. Journal of Mechanical Design, 2013, 135(5): 1–10. |
| [5] | Jones M H, Velinsky S A. Kinematics of roller migration in the planetary roller screw mechanism[J]. Journal of Mechanical Design, 2012, 134(6): 579–580. |
| [6] | Aurégan G, Fridrici V, Kapsa P, et al. Experimental simulation of rolling-sliding contact for application to planetary roller screw mechanism[J]. Wear, 2015, 332/333: 1176–1184. DOI:10.1016/j.wear.2015.01.047 |
| [7] | Matthew H J, Steven A V. Stiffness of the roller screw mechanism by the direct method[J]. Mechanics Based Design of Structures & Machines, 2014, 42(1): 17–34. |
| [8] | Tong R. A frictional heat model of planetary roller screw mechanism considering load distribution[J]. Mechanics Based Design of Structures & Machines, 2015, 43(2): 164–182. |
| [9] |
付晓军, 刘更, 马尚君, 等.
行星滚柱丝杠副螺旋曲面啮合机理研究[J]. 机械工程学报, 2016, 52(3): 26–33.
FU Xiaojun, LIU Geng, MA Shangjun, et al. Studies on meshing mechanism of helical surfaces in planetary roller screw mechanism[J]. Journal of Mechanical Engineering, 2016, 52(3): 26–33. (in Chinese) |
| [10] |
马尚君. 行星滚柱丝杠副结构设计方法及其传动性能研究[D]. 西安: 西北工业大学, 2013. MA Shangjun. Research on structure design method andtransmission performances of planetary roller screw[D]. Xi'an: Northwestern Polytechnical University, 2013. (in Chinese) |
| [11] |
马尚君, 刘更, 周建星, 等.
行星滚柱丝杠副运转过程动态特性分析[J]. 振动与冲击, 2013, 32(3): 167–171, 187.
MA Shangjun, LIU Geng, ZHOU Jianxing, et al. Dynamic characteristic analysis of a planetary roller screw in operating process[J]. Journal of Vibration and Shock, 2013, 32(3): 167–171, 187. (in Chinese) |
| [12] |
李凯, 叶佩青, 周晓尧, 等.
精密行星滚柱丝杠的传动特性[J]. 光学精密工程, 2016, 24(8): 1908–1916.
LI Kai, YE Peiqing, ZHOU Xiaoyao, et al. Driving characteristics of precision planetary roller screw[J]. Optical Precision Engineering, 2016, 24(8): 1908–1916. (in Chinese) |
| [13] |
张国庆, 杜建军.
基于螺旋理论的空间机构自由度分析方法[J]. 机械设计与制造, 2009(1): 10–12.
ZHANG Guoqing, DU Jianjun. Analysis of spatial mechanisms based on the screw theory[J]. Machinery Design and Manufacture, 2009(1): 10–12. (in Chinese) |
| [14] |
黄真, 刘婧芳, 曾达幸.
基于约束螺旋理论的机构自由度分析的普遍方法[J]. 中国科学(E辑:技术科学), 2009, 39(1): 84–93.
HUANG Zhen, LIU Jingfang, ZENG Daxing. A General method for the analysis of institutional degrees of freedom based on constrained screw theory[J]. Chinese Science (Series E: Technical Science), 2009, 39(1): 84–93. (in Chinese) |
| [15] |
黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006.
HUANG Zhen, ZHAO Yongsheng, ZHAO Tieshi. Advanced special mechanism[M]. Beijing: High Education Press, 2006. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41


