斜拉索是斜拉桥的主要承重构件之一，由于拉索系统长期承受交变荷载并暴露于自然环境中极易遭受环境腐蚀，在使用过程中远达不到桥梁的设计使用寿命。为确保桥梁运营安全，需定期检测斜拉索损伤状况，并及时更换损伤严重的斜拉索^[1]。如何利用无损检测方法确定拉索钢丝的锈蚀程度已成为斜拉桥安全运营维护中的关键问题之一。

目前，斜拉索腐蚀问题的研究局限在无应力状态下的材料腐蚀与静态荷载下的应力腐蚀问题，对拉索疲劳问题的研究大多针对疲劳荷载作用而没有考虑环境腐蚀的耦合作用效应^[2-3]。Barton等^[4]通过人工加速腐蚀试验方法研究镀锌钢丝在NaCl腐蚀介质中的腐蚀行为，重点探讨了静态荷载作用下钢丝腐蚀破裂、氢脆变化情况，获取钢丝样品失重量、氢浓度、延伸率等信息，其腐蚀体系是代表海洋环境的NaCl溶液。Furuya等^[5]采用2 m长拉索样品在自然环境(温度13~23 ℃，相对湿度30%~100%)中进行暴露试验，研究发现，索内水分和高温是形成索内恶劣腐蚀环境的主要原因。在拉索腐蚀程度评判方面，常用的方法是根据腐蚀图例的定性描述对拉索腐蚀状况进行主观分级，评定结果主观性较大^[6-7]。近年来，一些学者将小波理论应用于金属腐蚀行为的研究中，通过对金属腐蚀图像的小波变换，提取与腐蚀参数相关的特征值，寻求一种基于图像识别技术的无损检测方法^[8-9]。刘立平^[10]等通过提取不同腐蚀时长下海水介质中AZ40镁合金图像的灰度分布方差、二值化图像前景面积以及小波能量特征参数，发现腐蚀图像的小波能量与腐蚀阻力参数存在一定的相关性。李智^[11]提出了基于计算机图像处理技术的腐蚀坑三维特征提取方法，并在此基础上对不同的腐蚀损伤表征参量进行了统计分析，采用当量裂纹法对预腐蚀损伤铝合金进行疲劳寿命预测。

拉索索力中车辆荷载、大幅参数振动、风雨激振和涡激振动等活载效应显著，而疲劳荷载会加剧拉索腐蚀损伤的发展，特别是振幅高达1 m的拉索大幅风致振动会加剧锚管开裂、PE护套破裂等病害的发展，导致拉索钢丝暴露于腐蚀性环境中，进一步加剧拉索腐蚀损伤的发展。为真实模拟拉索的工作条件，将ZKD自锁式千斤顶张拉系统和盐雾腐蚀环境试验箱进行集成，研发了荷载盐雾锈蚀耦合试验系统，通过加速试验获得不同锈蚀等级下钢丝腐蚀图例及其力学性能参数，使用图像小波变换技术分析了腐蚀图例的表观特征，并重点分析了腐蚀小波图像能量特征值与钢丝失重量的相关性，实现了基于腐蚀小波图像分析的钢丝失重量预测。

1 锈蚀钢丝小波图像与腐蚀参数的回归模型 1.1 图像颜色模式和颜色通道(分量)的遴选

图像颜色模式是指用于记录和描述数字图像颜色的方式，常见的有RGB模式、HSV模式、位图模式、灰度模式、索引模式等。从图像学的角度审视钢丝的锈蚀过程，不难发现锈蚀形态的演变实际上是图像整体颜色特征和局部边缘轮廓特征的改变，不同颜色模式在描述图像整体色彩和局部轮廓方面各有优劣，因此，需要遴选对钢丝锈蚀形态变化较为敏感的颜色模式和模式分量作为描述钢丝锈蚀形态的图像量值。为初步遴选合适的图像量值，拟通过提取不同颜色模式下图像量值(如RGB模式下的G分量、HSV模式下的饱和度值)的均值M，并考察M与腐蚀参数的相关性，遴选相关度高的图像量值作为表征钢丝锈蚀程度的颜色分量，图像量值的均值为

$ M = \frac{1}{{m \times n}}\sum {f\left( {{x_1},{x_2}} \right)} , $

(1)

式中：M表示图像所有像素点量值的均值；x₁，x₂对应图像像素点坐标；f(x₁，x₂)表示图像在某颜色模式中某通道的量值。

1.2 腐蚀小波图像特征值的定义

研究表明，由小波变换得到的每一个小波子图像的特征值可反映图像的锈蚀形貌信息^[7-12]，且锈蚀图像差异性可以在小波分量中得到更好的体现，二维图像的二维连续小波变换可表示为

$ W\left( {a,{b_1},{b_2}} \right) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {f\left( {{x_1},{x_2}} \right){\psi _{a,{b_1},{b_2}}}\left( {{x_1},{x_2}} \right){\rm{d}}{x_1}{\rm{d}}{x_2}} } , $

(2)

$ {\psi _{a,{b_1},{b_2}}}\left( {{x_1},{x_2}} \right) = \frac{1}{{\sqrt a }}\psi \left( {\frac{{{x_1} - {b_1}}}{a},\frac{{{x_2} - {b_2}}}{a}} \right), $

(3)

式中：f(x₁, x₂)表示二维图像的某个量值(如灰度值、索引值、饱和度值)；W(a, b₁, b₂)为小波系数；ψ为小波基函数；x₁, x₂分别表示图像横向和纵向坐标；a为小波尺度因子；b₁，b₂为图像横向和纵向的平移因子。从式(1)中不难看出：连续小波变换涉及到卷积运算，计算困难，且将一个二维信号变换为三维小波系数，会造成严重数据冗余。鉴于此，实际应用中通常会对小波尺度因子和平移因子进行离散化处理^[13]：a=2^j，b₁=k₁×2^j, b₂=k₂×2^j (j为正整数)，并引入尺度函数φ(x₁, x₂)，使用著名的Mallat算法对信号进行多尺度分析，获得不同分解尺度下反映信号趋势项的低频小波系数W_Cj和反映信号细节项的高频小波系数W_Dj，低频小波系数反映了锈蚀图像整体颜色信息，高频小波系数反映了锈蚀图像的局部边缘信息。为描述钢丝锈蚀图像的整体颜色和锈蚀边缘轮廓信息，特定义以下指标：

$ {L_{{\rm{C}}j}} = \frac{1}{{m \times n}}{\left\| {{W_{{\rm{C}}j}}} \right\|_1} = \frac{1}{{m \times n}}\sum {\left| {{W_{{\rm{C}}j}}} \right|} , $

(4)

$ {L_{{\rm{D}}j}} = \frac{1}{{m \times n}}{\left\| {{W_{{\rm{D}}j}}} \right\|_1} = \frac{1}{{m \times n}}\sum {\left| {{W_{{\rm{D}}j}}} \right|} , $

(5)

$ {P_{{\rm{C}}j}} = \frac{{{{\left\| {{W_{{\rm{C}}j}}} \right\|}_1}}}{{{{\left\| {{W_{{\rm{D}}j}}} \right\|}_1} + {{\left\| {{W_{{\rm{C}}j}}} \right\|}_1}}}, $

(6)

$ {P_{{\rm{D}}j}} = \frac{{{{\left\| {{W_{{\rm{D}}j}}} \right\|}_1}}}{{{{\left\| {{W_{{\rm{D}}j}}} \right\|}_1} + {{\left\| {{W_{{\rm{C}}j}}} \right\|}_1}}}, $

(7)

其中：L_Cj和L_Dj分别为锈蚀图像第j层小波低频近似系数和高频细节系数的L₁范数均值，P_Cj和P_Dj分别为锈蚀图像第j层小波低频近似系数和高频细节系数的L₁范数的百分比。通过考察小波系数L₁范数均值和百分比与钢丝腐蚀参数的相关性，将相关度较高的图像特征参数作为回归模型中的自变量。

1.3 腐蚀钢丝小波图像特征值与腐蚀特征参数的回归模型

按照多元线性回归理论，以拉索钢丝腐蚀图像小波系数L₁范数均值(L_Cj和L_Dj)和百分比(P_Cj和P_Dj)为自变量，钢丝腐蚀参数W为应变量，并假定用于回归分析的拉索钢丝样本数量为n，则钢丝腐蚀图像特征值与腐蚀参数的回归模型可表示为

$ \mathit{\boldsymbol{W}} = \mathit{\boldsymbol{L\beta }} + \mathit{\boldsymbol{\varepsilon }}, $

(8)

其中：$ \mathit{\boldsymbol{W}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{W_1}}\\ \vdots \\ {{W_n}} \end{array}} \right] $，$ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} 1&{L_{{\rm{C}}m}^1}&{L_{{\rm{D}}1}^1}& \cdots &{L_{{\rm{D}}m}^1}&{P_{{\rm{C}}m}^1}&{P_{{\rm{D}}1}^1}& \cdots &{P_{{\rm{D}}m}^1}\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1&{L_{{\rm{C}}m}^n}&{L_{{\rm{D}}1}^n}& \cdots &{L_{{\rm{D}}m}^n}&{P_{{\rm{C}}m}^n}&{P_{{\rm{D}}1}^n}& \cdots &{P_{{\rm{D}}m}^n} \end{array}} \right] $，$ \mathit{\boldsymbol{\varepsilon }} = \left[ {\begin{array}{*{20}{c}} {{\varepsilon _1}}\\ \vdots \\ {{\varepsilon _n}} \end{array}} \right], \mathit{\boldsymbol{\beta }} = \left[ {\begin{array}{*{20}{c}} {{\beta _0}}\\ \vdots \\ {{\beta _{2m + 2}}} \end{array}} \right] $，m为腐蚀图像小波分解层数，ε为零均值正态分布随机向量，用于描述回归模型中随机干扰因素。在钢丝腐蚀参数W和腐蚀图像特征值L已知的情况下，利用最小二乘法即可获得回归系数β的点估计：

$ \mathit{\boldsymbol{\hat \beta }} = {\left( {{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right)^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{W}}。$

(9)

按照假设检验的相关理论，计算统计指标$ \tilde F $和t_k(k=1, …, 2m+2)，并与某置信水平所对应的概率分位值进行对比，可实现对回归模型和回归系数的显著性检验，

$ \tilde F = \frac{{\sum\limits_{i = 1}^n {{{\left( {{{\hat W}_i} - \bar W} \right)}^2}} /\left( {2m + 2} \right)}}{{\sum\limits_{i = 1}^n {{{\left( {{W_i} - {{\hat W}_i}} \right)}^2}} /\left( {n - 2m - 3} \right)}}, $

(10)

$ {t_k} = \frac{{{{\hat \beta }_k}/\sqrt {{\rm{diag}}{{\left[ {{{\left( {{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right)}^{ - 1}}} \right]}_k}} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{W_i} - {{\hat W}_i}} \right)}^2}} /\left( {n - 2m - 3} \right)} }}, $

(11)

其中：下标i表示第i个钢丝样本(i=1, …, n)；k表示第k个腐蚀图像特征值；$ {\mathit{\boldsymbol{\hat W}}_i} = {\mathit{\boldsymbol{L}}_{i \cdot }}\mathit{\boldsymbol{\hat \beta }}, {\mathit{\boldsymbol{L}}_{i \cdot }} $为L矩阵中第i个钢丝样本所对应的行向量，$ \bar W = \sum\limits_{i = 1}^n {{W_i}/n} $。

2 交变荷载与盐雾环境耦合作用下钢丝锈蚀加速试验

为模拟斜拉索服役状况下斜拉索交变荷载与环境腐蚀的耦合作用，依托重庆交通大学山区桥梁与隧道工程国家重点实验室培育基地，将ZKD自锁式千斤顶张拉系统和盐雾腐蚀环境试验箱进行集成，研发了荷载盐雾锈蚀耦合试验系统(如图 1所示)。在进行交变荷载和盐雾加速试验时，选用同一批次8×5=40根极限强度为1 860 MPa的Φ5.2 mm镀锌高强度钢丝，称重后将其穿过盐雾箱箱壁(使用防水胶套实现防水)锚固于C40混凝土反力翼墙上，并通过定时调整千斤顶的油压实现交变荷载的施加(其中钢丝交变应力上限取744 MPa，下限取544 MPa，荷载交变周期为4 h)，盐雾箱内盐雾沉降率设定为125 mL/m²·h，试验温度设定50 ℃。

试验中每次调整钢丝持载应力时，观察钢丝表观腐蚀形态，并根据《公路桥梁技术状况评定标准》(JTGT H21—2011)中拉索锈蚀等级的定性描述判断钢丝的腐蚀进程，当钢丝腐蚀形态与《公路桥梁技术状况评定标准》中某一等级的定性描述相吻合时，将同组4根钢丝取出，烘干后使用Nikon D610单反相机在室内相同灯光条件下进行拍照，每次拍照时使用相同的光圈大小和快门速度，以保证腐蚀图像具有相同的曝光度，再使用图像处理软件Photoshop去除腐蚀钢丝的背景部分，获得相应腐蚀图例照片，再用10%的稀硫酸擦拭钢丝试样，去除表面的锈蚀物后，测量钢丝重量获取各级腐蚀等级下钢丝失重量；将酸洗后的钢丝放在万能拉伸试验机上进行破坏试验，以获取其抗拉强度和延伸率。对于同一腐蚀等级的钢丝重复做2次试验获得8个样本图像及相应失重量，使用统计手段剔除偏离均值最远的样本，最终遴选出5根钢丝制作5个腐蚀等级对应腐蚀图例，如表 1所示。可以看出：交变应力和盐雾环境耦合作用下钢丝并非均匀腐蚀，而是呈现出明显的局部坑蚀现象；五级锈蚀图例的颜色和亮度差异较大，随着钢丝锈蚀加重，钢丝表观颜色经历了银白色、白斑、红斑、褐色以及深褐色的变化，锈蚀等级达到Ⅲ级后伴随着局部坑蚀的出现腐蚀图像亮度分布更加复杂，局部蚀坑轮廓边缘清晰。

表 2给出了腐蚀图例中各钢丝对应的锈蚀失重量、名义抗拉强度和断后延伸率，其中，腐蚀失重量已换算为单位长度的失重量，是钢丝锈蚀程度最重要的评价指标；名义抗拉强度是钢丝破断荷载与其公称面积之比；断后延伸率为钢丝拉伸断裂后的总伸长与原始标距长度的百分比，用以评价材料的延性。

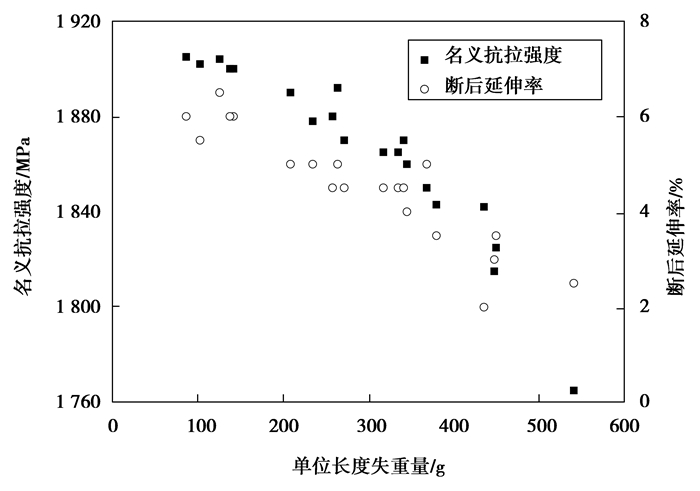
从图 2给出的钢丝名义强度和断后延伸率随钢丝锈蚀失重量的变化趋势中不难发现，随着钢丝锈蚀失重量的增加，钢丝名义抗拉强度和断后延伸率均逐渐减小，名义抗拉强度的减小表明，锈蚀钢丝的承载力会随着腐蚀的加重而减小，且两者之间相关性较好，因此，可以用钢丝锈蚀失重量近似地判断钢丝承载力的变化。而钢丝断后延伸率的降低则表明随着腐蚀程度的加重，钢丝延性能力将逐渐下降，这可能是由于钢丝锈蚀后部分截面面积减小严重而出现应力集中现象所导致的。

3 腐蚀钢丝小波图像分析及力学性能预测

钢丝锈蚀失重量是其锈蚀程度最直观的表现，文中将以锈蚀失重量作为应变量，使用回归模型尝试寻找并建立腐蚀图像小波能量特征值与钢丝锈蚀失重量的回归关系。

3.1 灰度、HSV和RGB颜色模式中颜色分量的选取

灰度模式将图像中每个像素使用1个0(黑色)到255(白色)之间的亮度值进行描述，图像的亮度信息可以较好地反映图像的边缘轮廓及纹理等局部特征，铝、镁等有色金属腐蚀程度的判定中经常使用灰度图像。RGB颜色模式是通过对红(R)、绿(G)、蓝(B) 3个颜色通道的混合叠加来得到不同的颜色，R、G、B的量值大小表示3种颜色分量的亮度值，RGB颜色模式对图像的描述方式和灰度模式是一样的，只是颜色通道不同而已。因此，RGB颜色模式中的R、G、B分量也可以作为钢丝腐蚀图像的特征指标。HSV颜色模式作为一种比较直观的颜色模型，由色调(H)、饱和度(S)、明度(V)3个参数表示，饱和度反映图像颜色的浓度变化，随着钢丝锈蚀加重，钢丝表观颜色经历了银白色、白斑、红斑、褐色以及深褐色的变化，HSV模式中的饱和度可以作为钢丝腐蚀图像的一项特征指标。

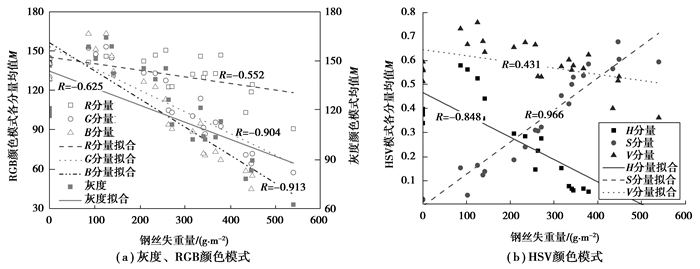
为遴选用于相关分析的灰度、HSV和RGB模式中的颜色通道，按照式(1)分别计算了5种腐蚀等级下钢丝腐蚀图例在灰度、HSV和RGB 3种颜色模式中各颜色通道量值的均值，并与钢丝失重量进行相关分析，结果如图 3所示。从图 3(a)中可以看出：锈蚀初期钢丝镀锌层锈蚀产生的白锈导致图像亮度有所增加，使得各颜色通道(灰度、R、G、B)量值增大，随着钢丝表面红锈的出现和增多，腐蚀图例各颜色通道的量值均逐渐减小；对比灰度、R、G、B 4种颜色通道量值随失重量的变化规律，不难发现蓝色通道量值与钢丝失重量的相关性最好。从图 3(b)中可以看出：腐蚀图例饱和度(S)随钢丝失重量的增加而增大，而腐蚀图例色调(H)、明度(V)则随钢丝失重量增加而减小；相比色调(H)，图像饱和度(S)和明度(V)与钢丝失重量的相关度更高，表明钢丝腐蚀历程中腐蚀形态的改变主要体现在颜色和亮度的改变，而亮度上的变化则集中在蓝色通道上。综上所述，可选取HSV颜色模式中的饱和度分量(S)和RGB颜色模式中的蓝色分量(B)用于后续分析。

3.2 腐蚀图像特征指标的优化选取

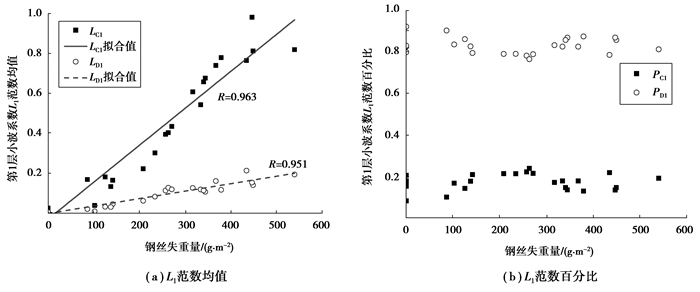
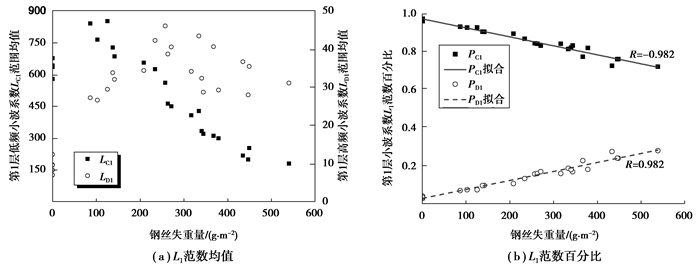
图像颜色分量均值反映了腐蚀图像整体颜色的变化，不能描述图像局部细节变化，为更好地表征钢丝锈蚀图像特征的定量指标，借鉴文献[9-12]的研究方法，使用haar小波分别对HSV颜色模式中的饱和度分量及RGB颜色模式中的蓝色分量图像进行1层小波分解，按照公式(4)~(7)计算小波系数L₁范数均值和百分比，结果如图 4和图 5所示。

从图 4中可以发现：相比于腐蚀图例小波系数L₁范数百分比，HSV颜色模式中S分量小波系数L₁范数均值与钢丝锈蚀失重量的相关度更高，且小波低频系数L₁范数均值L_C1对钢丝失重量的变化更为敏感；相比于Ⅲ级和Ⅳ级图例，Ⅱ级和Ⅴ级腐蚀图例的L_C1与钢丝失重量的相关性较差，这是由于腐蚀初期(Ⅱ级)钢丝表面氧化膜破裂后出现白锈，相比于钢丝无锈蚀状态时银白色表面，图像颜色变化不明显，而对于Ⅴ级腐蚀图例，试件基本被红锈覆盖，整体颜色变化也不明显，反映图像整体颜色浓度的饱和度分量(S)不能很好地捕捉图像的变化特征。但由于坑蚀的存在，Ⅱ级和Ⅴ级腐蚀图例局部轮廓有较大区别，可以进一步挖掘腐蚀图像特征信息。

从图 5可以发现：相比于腐蚀图例小波系数L₁范数均值，RGB颜色模式中B分量小波系数L₁范数百分比与钢丝锈蚀失重量的相关性更好，且低频系数和高频系数L₁范数百分比与钢丝失重量的相关度一致，可以选择其中一项指标描述腐蚀图像的边缘轮廓特征；相比于Ⅳ级和Ⅴ级腐蚀图例，Ⅱ级和Ⅲ级腐蚀图例的P_c1与钢丝失重量的相关性更好，这是由于Ⅱ级和Ⅲ级腐蚀图例中坑蚀特征更为明显，图像蚀坑周围颜色的显著变化等价于灰度图像亮度值的突变，小波变换后图像细节分量的亮度值能更好地表征钢丝坑蚀特征，在一定程度上弥补了HSV颜色模式中饱和度分量在刻画钢丝Ⅱ级腐蚀图例特征上的不足。

3.3 腐蚀钢丝图像特征值与力学性能的回归分析

鉴于HSV模式中的饱和度分量的低频小波系数L₁范数均值L_C1和RGB模式中的蓝色分量的高频小波系数L₁范数百分比P_D1，分别从不同层面反映了钢丝腐蚀特征，可同时使用该2项指标建立锈蚀钢丝力学性能的回归模型。需要说明的是，考虑到样本数量大小会影响到回归模型估计结果稳定性，根据文献[15]中以残差平方和的相对稳定性表征回归方程的稳定性，并以此构造估计统计量来确定样本容量为25时回归方程的稳定性，通过分析发现，相对误差为0.1时，样本容量为25的置信水平有90%，可认为文中选取的样本数量较为合理。

使用HSV模式中饱和度分量的低频小波系数L₁范数均值L_C1和RGB模式中蓝色分量的高频小波系数L₁范数百分比P_D1，作为钢丝腐蚀图例的特征参数，按照式(8)可建立算例腐蚀图例与失重量或名义抗拉强度的回归模型：

$ \left[ {\begin{array}{*{20}{c}} {{W_1}}\\ \vdots \\ {{W_{25}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{L_{C1}^1}&{P_{D1}^1}\\ \vdots&\vdots&\vdots \\ 1&{L_{C1}^{25}}&{P_{D1}^{25}} \end{array}} \right]\mathit{\boldsymbol{\beta }} + \mathit{\boldsymbol{\varepsilon }}。$

(12)

将25组钢丝腐蚀图例及相应的失重量或名义抗拉强度带入式(12)，利用最小二乘法即可分别获得失重量和名义抗拉强度所对应的β点估计：

$ \mathit{\boldsymbol{\hat \beta }} = {\left[ {\begin{array}{*{20}{c}} { - 28.0}&{167.8}&{1411.5} \end{array}} \right]^{\rm{T}}}, $

(13)

$ \mathit{\boldsymbol{\hat \beta }} = {\left[ {\begin{array}{*{20}{c}} {1931.7}&{ - 66.2}&{ - 177.1} \end{array}} \right]^{\rm{T}}}。$

(14)

按照式(10)和式(11)分别计算统计指标$ \tilde F $、t₁、t₂，并取95%的置信水平对回归模型式(12)和回归系数式(13)和式(14)进行显著性检验，检验结果如表 3所示，显然统计指标$ \tilde F $、t₁、t₂均大于95%置信水平下的分位数，表明拉索钢丝失重量和名义抗拉强度与L_C1和P_D1均有显著的线性相关性(95%的置信水平)。

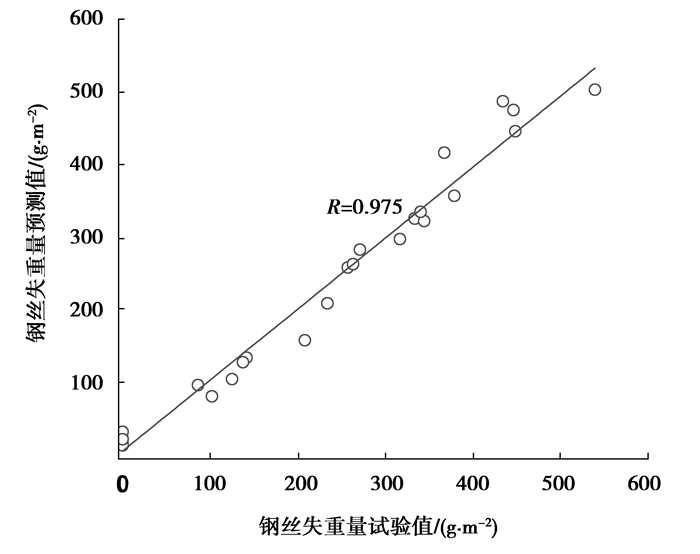
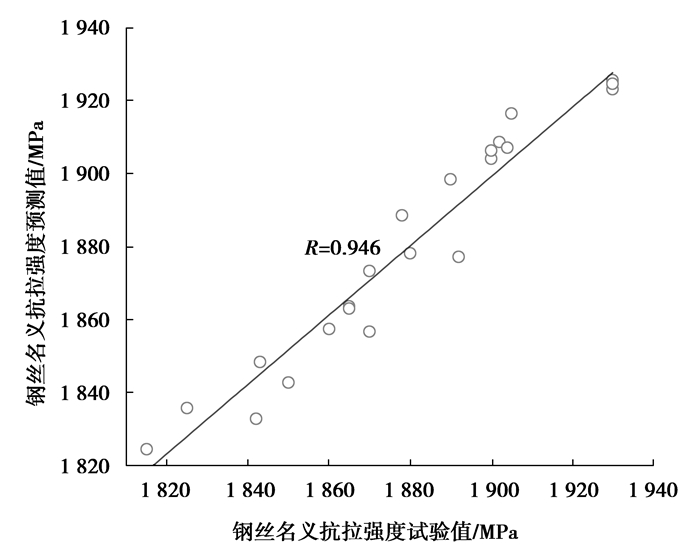
利用表 1中钢丝腐蚀图例及式(12)所示的回归模型，可计算出腐蚀图例所对应的钢丝失重量和名义抗拉强度预测值，图 6~图 7给出了基于拉索钢丝腐蚀图像处理的失重量和名义抗拉强度预测值与试验实测值的对比，两者相关系数均超过0.9。显然，采用文中所述方法可以很好地实现基于拉索钢丝腐蚀图像分析的钢丝失重量和名义抗拉强度的预测。

4 结论

1) 交变荷载和盐雾环境耦合作用下拉索钢丝不是均匀锈蚀的，而是呈现出明显的局部坑蚀现象，随着钢丝锈蚀失重量的增加，钢丝名义抗拉强度和断后延伸率均逐渐减小。

2) 钢丝腐蚀历程中腐蚀形态的改变主要体现在颜色浓度和亮度的改变，且HSV色彩模式中的饱和度分量可较好地反映钢丝锈蚀图像整体颜色的变化，而RGB色彩模式中的蓝色分量可较好地反映钢丝锈蚀图像局部亮度的变化。

3) 相比色调(H)和明度(V)，HSV颜色模式中饱和度(S分量)的小波系数L₁范数均值与钢丝锈蚀失重量的相关度更高；相比灰度模式、RGB模式中的红色和绿色通道而言，RGB颜色模式中蓝色通道的小波系数L₁范数百分比与钢丝锈蚀失重量的相关性更好。

4) 拉索钢丝腐蚀图像与腐蚀失重量、名义抗拉强度之间存在良好的线性回归关系，利用拉索钢丝腐蚀图像及文中提出的回归模型可以较好地预测钢丝锈蚀失重量和名义抗拉强度。