随着经济水平提高,汽车保有量急剧上升, 到2015年底全国机动车保有量达到2.79亿[1],由于与之配套的道路交通设施发展滞后和日益加快的生活节奏,使得油耗浪费、交通拥堵等问题日益突出。人们希望避免拥堵,节省油耗,从而提高出行效率[2-4]。若驾驶员不熟悉路况或不了解交管信息,不仅会造成不必要的油耗和违章罚单,也会加剧交通拥堵,存在严重交通隐患。
为减少油耗,目前采取的经济性驾驶技术主要有3类:强化驾驶员节油教育、节油驾驶辅助技术和经济性自动驾驶[5-7]。节油教育增加驾驶员额外负担,自动驾驶技术目前尚不成熟,离普及还有一定距离。节油驾驶辅助技术通过规划行车路径为驾驶员提供节油建议,既不增加负担,技术也较成熟,是当前最经济有效的节油方式。
针对节油辅助驾驶技术,人们提出了多种减少油耗的路径规划算法。一类是根据路网的理论油耗,基于油耗权值的Dijkstra算法和Floyd算法,在车辆行驶前规划出一条最优油耗路径[8-11]。另一类最优油耗路径规划模型是从概率的角度出发,综合分析油耗的各个影响因素,例如:车辆类型、路况、坡度、风阻系数等,将问题变为一个NP问题,求取最优解[12-14]。但上述算法只在车辆行驶前对路径进行规划,并未考虑行驶过程中的道路车流量变化。然而交通状况瞬息万变,必须实时规划路径才能较为理想地实现最优油耗。
因此,提出一种依托车联网,基于路由选择的最优油耗路径规划模型,能够实时准确地反映交通路网中各道路的实时路况,从而实时规划路径,实现出行油耗最优。
1 最优油耗路径规划建模车流量是影响汽车油耗的一个重要因素,其具有突发性和随机性的特点[15-16]。对于同一道路,在车流量不同的情况下,实际油耗也不同。车流量与通信中的网络延迟有相似特点。在通信网络中,一般利用合适的路由算法进行流量控制,具有自适应性、稳定性、公平性等优点。但因车辆的个体差异性和驾驶员的主观因素,无法得到确切的油耗值,通过路阻函数反应道路基本属性,从而间接反应路况对汽车油耗的影响,并着重考虑实时车流量,提出基于路由选择的最优油耗路径规划模型。
1.1 路由节点设置把路网看作一张无向图,对整个路网进行节点设置。每个节点生成各自的路阻路由表,各节点的信息储存在车联网控制中心。节点设置时需满足2个要求:一是节点尽可能少,二是在节点处尽可能有更多路径选择。岔路口是各个不同方向的车辆汇合和转向的地方,而单向道的车流没有分流和聚合,理想认为单向道各个部分的车流量相等。因此在岔路口布置节点可以满足上述节点布置要求。令所有节点pi组成路网节点集合P,P={p1, p2…pi, …pn}。
1.2 道路路阻函数确定忽略车型和驾驶员主观因素造成的油耗差异,主要考虑实时车流量的影响,假定在道路通畅情况下,车辆均以道路的最大限速进行行驶。因此道路通畅情况下,油耗F是路阻r的正相关函数,F=f(r)。而路阻函数用来表示通行时间与道路通行能力之间的关系,其路阻r又与通行时间t成正比函数,r=g(t),则油耗与通行时间成正比,F=f(r)=f(g(t))。但在现实生活中,每辆车的平均油耗值不同,但实际油耗是根据本身情况进行考虑的。通行时间不便记录,且记录不够精确,因此选择使用路阻值进行计算。
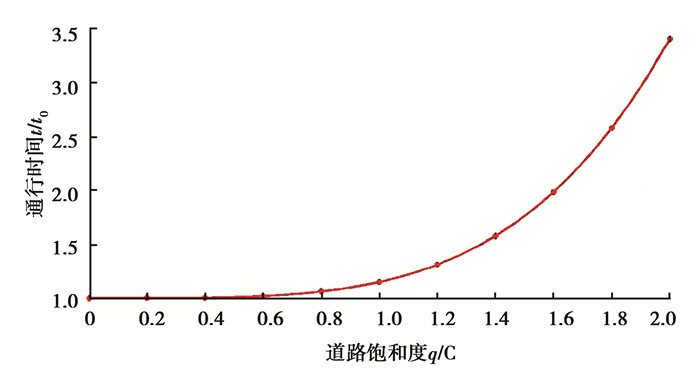
路阻函数与道路通行能力紧密相关。道路最大通行能力C反应道路能够承担车辆的极限值,表示在单位时间内能通过的最大车流量。q为当前道路的实际车流量。根据美国公路局的BPR函数(U.S.bureau of public roads)[17],通行时间路阻函数为r,则
| $ r = \left[ {1 + \alpha {{\left( {\frac{q}{C}} \right)}^\beta }} \right]{t_0}, $ | (1) |
其中:
|
图 1 BPR曲线图 Figure 1 The BPR curve graph |
从图 1中可以看出,
原路阻函数只考虑了畅通时间与油耗的关系,并没有考虑实际行驶中存在的怠速情况。因此,对原路阻函数进行改进,其仍与油耗呈正相关,但将实际通行时间t分为畅通时间t0和怠速时间t-t0,t0畅通时间,即车辆在道路上正常行驶、未出现拥堵停滞的行驶时间。经过研究发现对于主流私家车,大致怠速4 min相当于以60 km/h行驶1 min的油耗[18],因此,在道路拥堵情况下,油耗如式(2)表示
| $ F = f\left( {{t_0}} \right) + \frac{1}{4}f\left( {{t_0} - t} \right)。$ | (2) |
改进后的实际畅通行驶时间t0'如式(3)表示
| $ {{t'}_0} = {t_0} + \frac{1}{4}\left( {t - {t_0}} \right)。$ | (3) |
改进后的路阻函数r'为
| $ r' = g\left( {t'} \right) = g\left( {\left[ {1 + \alpha {{\left( {\frac{q}{C}} \right)}^\beta }} \right]{{t'}_0}} \right) = g\left( {\left[ {1 + \alpha {{\left( {\frac{q}{C}} \right)}^\beta }} \right]\left[ {{t_0} + \frac{1}{4}\left( {t - {t_0}} \right)} \right]} \right)。$ | (4) |
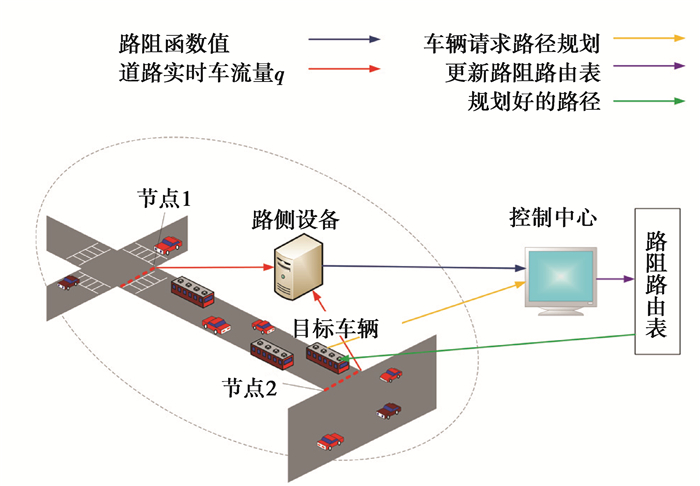
改进后的路阻函数r'可间接反应道路的油耗水平,避免因为车型和驾驶员主观因素对油耗造成的差异性, r'越大表示该段路油耗越大。实际路阻值的获取和存储过程如图 2所示,路侧设备实时采集车流量数据q,计算该路段路阻值,并周期性地将其传给控制中心,控制中心按照提出的路径规划算法实时更新路阻路由表。目标车辆只需请求查询路阻路由表即可获得控制中心反馈的最优油耗路径。
|
图 2 信息获取示意图 Figure 2 The diagram of information acquisition |
最优油耗路径规划在车联网系统的控制中心完成,并避免针对每个车辆单独进行路径规划,可以大大提高实时性。控制中心采用Djkstra算法[19-21],假定2节点间交通情况不变,在研究中将路阻值作为权值,计算路网中任意2点之间的最短路径,将各点之间的最小路阻路径存储在路由表中,在该节点处的车辆只需查询相应路由表即可确定路径,具体步骤如下。
将路网看作一张有权无向图G,已知路网中的节点数为n,所有节点构成集合P,第i个节点用pi表示;路网中每条道路的路阻函数值初始为r0, ru, w表示邻接矩阵的u行w列坐标路阻值。以此构建路网的邻接矩阵
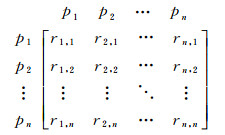
|
图 3 邻接矩阵(G) Figure 3 adjacent matrix(G) |
将节点集合P中的节点分为2部分,一部分为已知最短路径的集合,用S表示(S初始值只有起点一个元素);另一部分是未知最短路径的集合,用U表示,每当确定一个最短路径时则将该节点加入到S中。引入2个向量Ppath和Proad用来记录任意起始节点pi到目的节点pj的路径和最小路阻值,以及一个中间计数向量Nnode。Ppath和Proad的初始态为:Ppath={pi},Proad={0, ∞, ∞, …, ∞},Nnode取1或0,用来记录pi是否被遍历,当sum(Nnode)=n时,算法执行完毕。
开始时, S={pi},ri, i=0,令中间量k=i。以pk为中间节点,寻找pk相邻节点中与pi最小路阻值的点pj,所以此时路阻值为:Proad[j]=ri, j=min{ri, k+rk, j|pi, pk, pj∈P}(k≠j)。
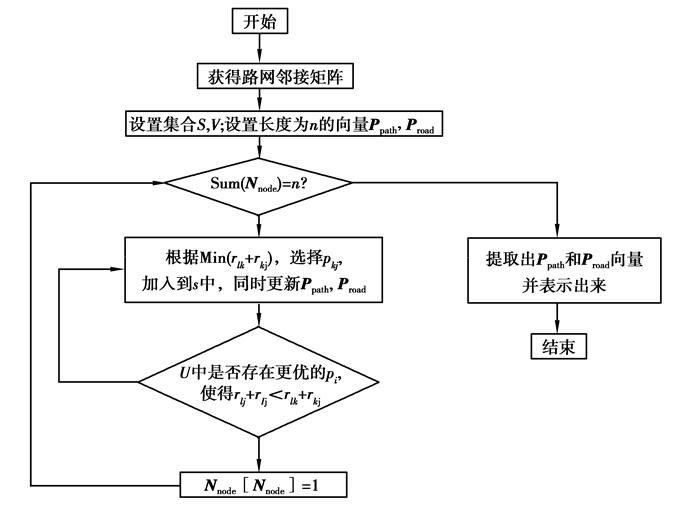
将最小路阻值的路径记录进Ppath中,表示为Ppath{pi→pk→pj}。而Nnode[j]=1,将已知最短路径的节点加入S中,S={pi…pj}。将G中从起点pi到其余各顶点的最小路阻值按升序排列,若某节点暂时未遍历到,则暂令ri, k=∞。按此顺序,依次将与pk相邻的节点pj的路阻值ri, j存入Proad中,在遍历中若存在r1, m+rm, j<r1, k+rk, j(vm∈U, vk∈S),则替换Ppath和Proad中相应的值,始终保持路阻值最小。算法的流程图如图 4所示,
|
图 4 算法流程图 Figure 4 The algorithm flow chart |
以图 5为例,线上数字代表已知的道路路阻,若以p1为起点,其构建路由表过程如下
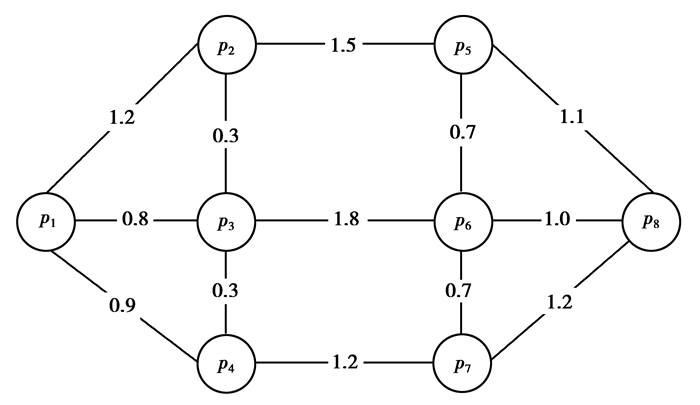
|
图 5 路网样例示意图 Figure 5 The diagram of sampled road network |
1) 起始时,选入p1,S={p1};U={p2, p3, p4, p5, p6, p7, p8},Ppath={p1};Proad={0, ∞, ∞, ∞, ∞, ∞, ∞, ∞}。已知r1, 2=1.2、r1, 3=0.8、r1, 4=0.9,更新Ppath和Proad;p1到其他节点无直接路径。
2)
3)
4) 把起点到剩余节点中路阻最小的节点pk,作为中间节点,重复2, 3步,直到集合U为空,则算法完成。
因此,可获得如表 1所示的p1路由表。
| 表 1 pi的路阻路由表 Table 1 Routing tables of road impedance pi |
从表 1可知,每个节点的路由表有n-1条,更换起点,重复上述步骤,得到路网中所有点的路由表。车辆只需根据目的点查询相应节点上的路由表即可获得已经规划好的最优油耗路径。
而控制中心则根据路侧系统返回的路阻值,不断重复执行本算法。当某条道路出现交通拥堵时,该道路的路侧系统返回的路阻值使得ru, w增大,重复上述算法时,可能导致相关节点的路由表发生变化从而达到对路径进行实时规划的目的。
2 仿真试验为验证本模型的可行性,利用Matlab模拟仿真实际交通路网,对比是否使用路由选择模型时,车辆行驶总路阻的变化(如图 6所示)。
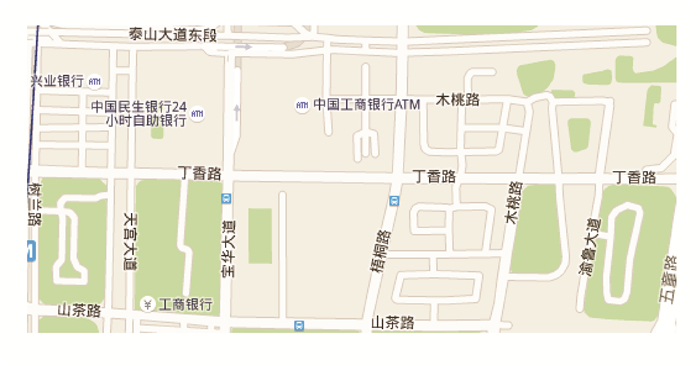
|
图 6 某典型路段的路网示意图 Figure 6 A schematic of typical road network |
图 6是重庆某典型路段的交通图。为适应软件仿真条件,将其抽象化为简单的无向图,在岔路口设置节点,道路用线段表示,线段上的数字表示该道路的路阻。为了简化示意图,原路网中的道路宽度、弯道等影响直观性的因素,在简化后的路网中并未体现,简化后的路网如图 7所示,其中红色数字为节点编号,黑色数字为该道路路阻。
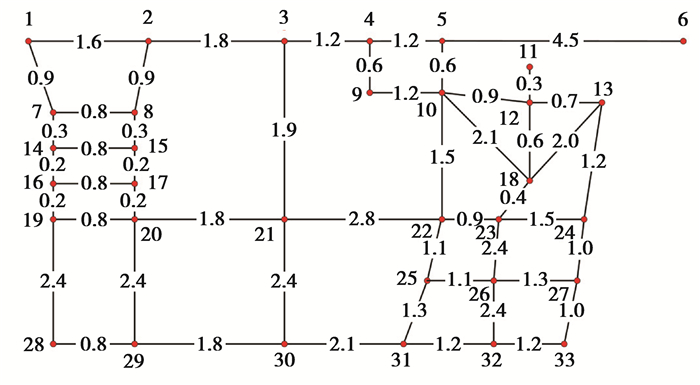
|
图 7 路网仿真图 Figure 7 The Simulation diagram of road network |
路网中运行的车辆都能够与路侧系统和控制中心通信,控制中心已建立相应的路由表,并且能够从路侧系统获得道路路阻值,更新路由表。实验时,路网中各条道路的路阻值会随时变化。测试车辆分为2组,第一组只在行驶前进行路径规划,第二组根据路侧系统返回的数据实时规划路径,分别对比2组车辆在不同交通状况下完成同一任务和在同一交通状况下完成不同任务的路阻值。
根据交通运行指数(TPI)将道路拥堵情况分为10级,由此来确定路阻值的变化范围,如表 2所示
| 表 2 交通运行指数(TPI)表 Table 2 Traffic operation index (TPI) |
当拥堵等级达到10级时,出行时间将增加1.1倍以上,可以得出r=5.58,表示拥堵路段的行驶时间是畅通时的5.58倍。带入式(3)中,拥堵与通畅时的路阻比值ζ∈[1, 2.1],存在随机值θ∈[1, ζ],使得若干条道路有不同的拥堵状况。
在不同的交通状况下从节点p1到达节点p13,车辆每到一个节点,路网信息会刷新,并且车辆会重新进行路径规划。2组测试车辆通过的道路路阻结果如图 8所示,路阻比ζ以0.05递增,路阻比越大节油效果越明显,同时,最优油耗路径规划也在改变。
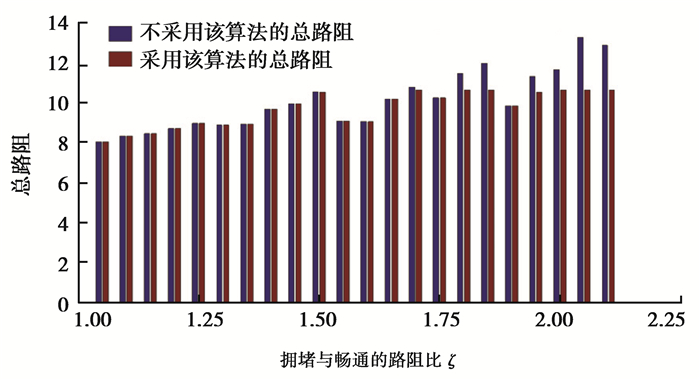
|
图 8 不同拥堵程度完成同一任务的总路阻对比 Figure 8 Compared with the road resistance in same task and different congestion |
在相同的交通状况下从节点p1出发到达不同节点,车辆每到一个节点,路网信息同样也会刷新,并且车辆会重新进行路径规划。测试车辆对于相同交通状况下随机选择3条不同起止点的线路进行仿真试验。试验一设置起始点为p1,终止点为p13,在道路畅通时依次通过的中间节点为p1;p2;p3;p4;p9;p10;p12;p13,而在拥堵状况下的路径规划变为p1;p7;p14;p16;p19;p20;p21;p22;p23;p18;p13。试验二设置起始点为p1,终止点为p6,在道路畅通时依次通过的中间节点为p1;p2;p3;p4;p5;p6,而在拥堵状况下的路径规划变为p1;p7;p8;p15;p17;p20;p21;p22;p10;p5;p6。试验三设置起始点为p1,终止点为p33,在道路畅通时依次通过的中间节点为p1;p2;p3;p21;p30;p31;p32;p33,而在拥堵状况下的路径规划变为p1;p7;p8;p15;p17;p20;p29;p30;p31;p32;p33。
以路网中有
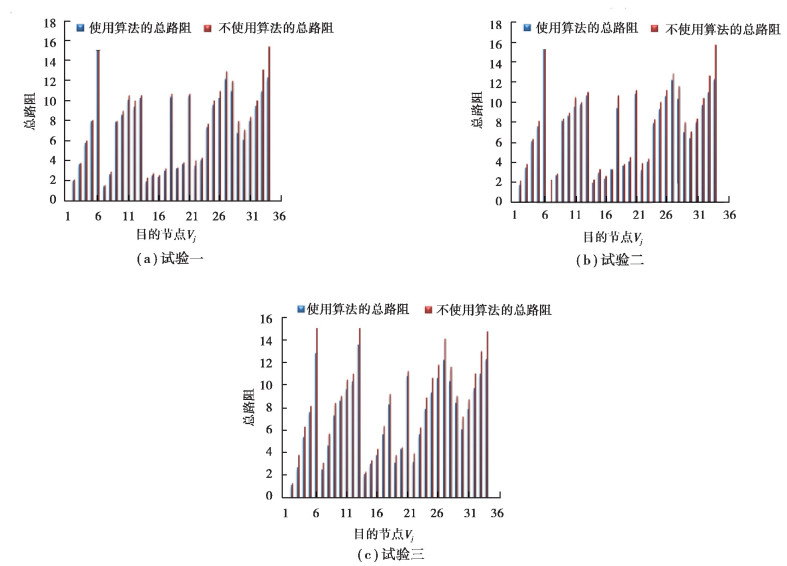
|
图 9 同一拥堵情况下完成不同任务的总路阻对比 Figure 9 Compared with the road resistance in same congestion and different tasks |
通过上述试验可知:不同交通状况下完成同一任务时,随着车流量的增大,即交通越拥堵,节能效果越明显。同一交通状况下完成不同任务时,当中间节点越多时,节能效果越明显。
3 结论提出的基于路由节点的最优油耗路径规划模型,在能够获取车流量反馈信息的前提下,实时更新交通路况,以便车辆行驶时能够实时获取最优油耗路径,在道路拥堵和长距离行驶时,可以绕过拥堵道路,从而减少出行油耗,实现经济出行,同时也能够间接地调度行驶车辆,减少交通拥堵。
| [1] |
国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 2015.
National Bureau of Statistics. China statistical yearbook[M]. Beijing: China Statistics Press, 2015. (in Chinese) |
| [2] |
蔡虹, 吴斌, 殷南晨.
以降低油耗为目标的车辆路径问题研究[J]. 实验科学与术, 2015, 13(3): 14–17.
CAI Hong, WU Bin, YIN Nanchen. Research on vehicle rounting problem for fuel consumption reduction[J]. Experiment Science and Technology, 2015, 13(3): 14–17. (in Chinese) |
| [3] |
许茂增, 余国印, 周翔, 等.
综合成本最小的低碳车辆调度问题及算法[J]. 计算机集成制造系统, 2015, 21(7): 1906–1914.
XU Maozeng, YU Guoyin, ZHOU Xiang, et al. Low-carbon vehicle scheduling problem and algorithm with minimum-comprehensive-cost[J]. Computer Integrated Manufacturing System, 2015, 21(7): 1906–1914. (in Chinese) |
| [4] | Singh V, Sharma S K. Fuel consumption optimization in air transport: a review, classification, critique, simple meta-analysis, and future research implications[J]. European Transport Research Review, 2015, 7(2): 1–24. |
| [5] |
徐中明, 陈旭, 贺岩松, 等.
智能交通系统(ITS)中的智能汽车技术[J]. 重庆大学学报, 2005, 28(8): 17–21.
XU Zhongming, CHEN Xu, HE Yansong, et al. Technologies of intelligent vehicle in intelligent transportation system (ITS)[J]. Journal of Chongqing University, 2005, 28(8): 17–21. DOI:10.11835/j.issn.1000-582X.2005.08.005 (in Chinese) |
| [6] | Singh V, Sharma S K. Evolving base for the fuel consumption optimization in Indian air transport: application of structural equation modeling[J]. European Transport Research Review, 2014, 6(3): 315–332. DOI:10.1007/s12544-014-0134-4 |
| [7] | Ahn K, Rakha H, Trani A, et al. Estimating vehicle fuel consumption and emissions based on instantaneous speed and acceleration levels[J]. Journal of Transportation Engineering, 2002, 128(2): 182–190. DOI:10.1061/(ASCE)0733-947X(2002)128:2(182) |
| [8] | Xiao Y, Zhao Q, Kaku I, et al. Development of a fuel consumption optimization model for the capacitated vehicle routing problem[J]. Computers & Operations Research, 2012, 39(7): 1419–1431. |
| [9] |
王树西, 李安渝.
Dijkstra算法中的多邻接点与多条最短路径问题[J]. 计算机科学, 2014, 41(6): 217–224.
WANG Shuxi, LI Anyu. Multi-adjacent-vertexes and multi-shortest-paths problem of Dijkstra algorithm[J]. Computer Science, 2014, 41(6): 217–224. DOI:10.11896/j.issn.1002-137X.2014.06.043 (in Chinese) |
| [10] | Pop P C, Matei O, Sitar C P, et al. An improved hybrid algorithm for solving the generalized vehicle routing problem[J]. Neurocomputing, 2013, 109(8): 76–83. |
| [11] | Ren G, Fan C, Hua J, et al. Analyses of unified congestion measures for interrupted traffic flow on urban roads[J]. Journal of Southeast University (English Edition), 2014, 30(1): 101–106. |
| [12] | Figliozzi M, Boudart J, Feng W. Economic and environmental optimization of vehicle fleets: impact of policy, market, utilization, and technological factors[J]. Transportation Research Record, 2011(2252): 1–6. |
| [13] |
蔡延光, 汤雅连, 蔡颢.
时变路网条件下车辆路径问题的自适应蚁群算法[J]. 计算机应用研究, 2015, 32(8): 2309–2312, 2346.
CAI Yanguang, TANG Yalian, CAI Hao. Adaptive ant colony optimization for vehicle routing problem in time varying networks environment[J]. Application Research of Computers, 2015, 32(8): 2309–2312, 2346. (in Chinese) |
| [14] | Windisch E. The uptake of electric vehicles in the Paris region: A financial analysis of total costs of ownership[R]. Scotland: European Transport Conference, 2011. |
| [15] |
李进, 傅培华, 李修琳, 等.
低碳环境下的车辆路径问题及禁忌搜索算法研究[J]. 中国管理科学, 2015, 23(10): 98–106.
LI Jin, FU Peihua, LI Xiulin, et al. Study on vehicle routing problem and tabu search algorithm under low-carbon environment[J]. Chinese Jounral of Management Science, 2015, 23(10): 98–106. (in Chinese) |
| [16] |
李林波, 吴兵, 潘弘, 等.
城市道路路段拥挤交通流特性研究[J]. 山东交通学院学报, 2010, 18(1): 13–16.
LI Linbo, WU Bing, PAN Hong, et al. Research on the traffic flow characteristics of the congested sections of ubran road[J]. Jounral of Shandong Jiaotong University, 2010, 18(1): 13–16. (in Chinese) |
| [17] |
王树盛, 黄卫, 陆振波.
路阻函数关系式推导及其拟合分析研究[J]. 公路交通科技, 2006, 23(4): 107–110.
WANG Shusheng, HUANG Wei, LU Zhenbo. Deduction of link performance function and its regression analysis[J]. Journal of Highway and Transportation Research and Development, 2006, 23(4): 107–110. (in Chinese) |
| [18] |
张宝中.
汽车怠速油耗对整车油耗的影响和思考[J]. 职业技术, 2016, 15(9): 101–102.
ZHANG Baozhong. Thinking and effect of vehicle idle oil consumption on ordinary vehicle oil consumption[J]. Vocational Technology, 2016, 15(9): 101–102. (in Chinese) |
| [19] | Bellis V D, Bozza F, Siano D, et al. Fuel consumption optimization and noise reduction in a spark-ignition turbocharged VVA engine[J]. SAE International Journal of Engines, 2013, 6(2): 1262–1274. DOI:10.4271/2013-01-1625 |
| [20] | Meng Z, Pan J S. Monkey king evolution: a new memetic evolutionary algorithm and its application in vehicle fuel consumption optimization[J]. Knowledge-Based Systems, 2016, 97: 144–157. DOI:10.1016/j.knosys.2016.01.009 |
| [21] | Lin L, Qian W, Adel W. A combined M5P tree and hazard-based duration model for predicting urban freeway traffic accident durations[J]. Accident Analysis & Prevention, 2016, 91: 114–126. |
 2018, Vol. 41
2018, Vol. 41

