机床床身在使用过程中最常见的故障模式是尺寸精度下降, 引起精度下降的主要原因是残余应力的释放[1-2]。现阶段国内工厂大量采用热时效的方法消除零件的残余应力。床身残余应力消除水平决定了热时效过程下的床身质量, 对其进行评价对提高零件质量和后续工作的开展有重大作用。文献[3]对重型机床基础件的热时效工艺进行研究优化以减小残余应力。文献[4]对热时效和振动时效消除残余应力的工艺过程、应力消除效果、成本等进行了介绍和比较。文献[5]利用软件对床身铸造和热时效过程进行仿真, 并对床身导轨残余应力值进行测量, 进而提出了热时效改进工艺。文献[6]对超长床身的热处理工艺进行了介绍, 提出了一些值得关注的点。文献[7]提出了一种基于模糊物元模型的数控装备质量评价方法。文献[8-9]着重研究了热时效对金属材料性能的影响。以上文献较侧重于热时效工艺、热时效影响或质量评价某一方面的研究, 系统地提出对热时效效果进行评价的方案还未见报道。
笔者从“5M1E”(即人员、机器、材料、方法、测量、环境)6个方面考虑热时效过程中床身质量的损失。运用模糊综合评价等方法对各因素进行评价, 得到的评价值可以推算出该影响因素的熵值, 再运用熵权法和基于Vague集的模糊评判计算各因素的权重(结合两种权重确定方法得到的综合权重更为客观和权威), 最后结合各因素初始评价值得出基于热时效过程的床身质量综合评价值。
1 热时效工艺下的床身质量评价模型信息熵是随机变量无约束程度的一种度量, 进一步说是概率的度量, 系统越无序, 熵值就越大, 系统越有序、越稳定, 熵值就越小[10-12]。文献[13]将“熵”带入质量工程领域, 描述产品被失去的质量, 提出“产品质量熵”的概念作为产品全生命周期中自身质量状态不确定性的一种度量, 即用于衡量质量的损失。就机床床身热时效过程而言, 热时效过程也会引起床身质量的损失, 笔者结合信息熵的概念提出基于热时效过程的“热时效熵”, 用以度量该过程床身质量的损失。
1.1 热时效熵的提出描述一个离散随机变量构成的离散信源(即产生消息、消息序列和连续消息的来源), 就是规定随机变量X的取值集合:设离散随机变量X具有n个不同的可能取值A={a1, a2, …, an}, 每个取值的概率P={p1, p2, …, pn}, 则
| $ \sum\limits_{i = 1}^n {{p_i} = 1, } $ |
式中:ai和pi(i=1, 2, …, n)分别表示该系统n个可能的状态及每个状态的发生概率。一般情况下, 记ai的信息量为I(ai):
| $ I({a_i}) = \ln (\frac{1}{{{p_i}}})。$ |
信源的平均不确定性应当为单个符号不确定性信息量I的统计平均值, 称为信息熵:
| $ H\left( x \right) = - k\sum\limits_{i = 1}^n {{p_i}\ln {p_i}, } $ |
式中k为比例系数, 取k=1/ln n。
基于以上信息熵的概念, 笔者提出“热时效熵”以表示热时效过程中由于操作不当、机器老化、工艺缺陷等影响对零件质量造成的损失。为解释热时效熵, 将热时效过程看作一个理想过程, 即零件经过热时效后残余应力完全消除, 视残余应力完全消除的状态为即时零件的最佳质量状态。然而生产实践中热时效后零件残余应力总有残余, 除去工艺本身达不到百分之百消除残余应力外, 可以认为是操作不当、机器老化、工艺缺陷等影响因素造成的残余应力消除水平下降, 残余应力消除水平下降即带来质量损失。从熵的角度出发, 其表现为质量的不确定度和无序度, 当熵值越大, 表示质量损失越严重。假如影响热时效过程零件质量的因素有n个, 将其作为熵值的信源中所描述的状态, 其中第i个影响因素的状态概率为Pi, 则热时效下零件质量的熵值为
| $ S = - k\sum\limits_{i = 1}^n {{p_i}\ln {p_i}, } $ |
其评定值用来衡量热时效过程中零件的质量损失状态, 其值越大, 质量越差。由熵值可推出各影响因素的熵权, 是综合评价权重的重要组成部分。
1.2 模糊综合评价方法模糊综合评价是一种常用综合评价方法, 在本文1.4节有应用, 其评价步骤[14-15]如下。
1) 确定评价对象的因素论域和等级论域。
| $ U = \{ {u_1}, {u_2}, \cdots , {u_n}\} , V = \{ {v_1}, {v_2}, \cdots , {v_m}\}。$ |
2) 建立模糊关系矩阵R。
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}& \cdots &{{r_{1m}}}\\ \vdots &{}& \vdots \\ {{r_{n1}}}& \cdots &{{r_{nm}}} \end{array}} \right]。$ |
矩阵中元素rij表示评价对象因素ui对vj等级的隶属度, 即评价对象在因素ui方面的评价。
3) 确定评价因素的权向量。
评价因素的权向量A={a1, a2, …, an}中的元素ai本质上是因素ui对整个评价对象的隶属度, 且
4) 合成模糊综合评价结果向量。
| $ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{A}} \circ \mathit{\boldsymbol{R}} = \{ {b_1}, {b_2}, \cdots , {b_m}\} , $ | (1) |
其中bj是由A与R的第j列运算得到的, 它表示被评事物从整体上看对vj等级模糊子集的隶属程度。
采用加权平均模型M(·, ⊕)合成算子得到向量B。计算公式为
| $ {b_j} = \sum\limits_i^n {({a_i} \cdot {r_{ij}})} = \min (1, \sum\limits_{i = 1}^n {{a_i} \cdot {r_{ij}}} ), $ | (2) |
式中bj, aj, rij分别为隶属于第j等级的隶属度, 第i个评价指标的权重和第i个评价指标隶属于第j等级的隶属度。
5) 分析模糊综合评价结果向量。
采用加权平均原则处理:V={v1, v2, …, vm}为各等级的秩, 然后用B中对应分量将各等级的秩加权求和, 从而得到被评价对象的相对位置, 其表达式为
| $ X = \sum\limits_{j = 1}^m {{b_j}^l{C_j}} /\sum\limits_{j = 1}^m {{b_j}^l} , $ | (3) |
式中:l为待定系数, 一般取1或2;Cj为根据评语集V给出的评分值, 它由相关领域专家基于历史数据和个人经验综合确定。
1.3 基于Vague集的模糊评判在确定各指标的影响权重时, 基于Vague集的模糊理论综合专家的支持、反对意见, 对模糊信息的表达较为全面, 使得确定的权重更有说服力[16]。指标权重确定方法如下所示[17]。
1) 设置赋权评分等级及其基准分值, 设评分等级为
| $ \alpha = \{ {\alpha _1}, {\alpha _2}, \cdots , {\alpha _m}\} , $ |
式中:αj为第j个评分等级的基准分值, j=1, 2, …, m;m为评分等级数。
因素的权重由P位专家按照制定的表决模型投票决定, 将因素ui的权重属于评分等级αj的可能范围表示为
| $ {\beta _{ij}} = \{ \left[ {{t_{ij}}\left( \alpha \right), 1 - {f_{ij}}\left( \alpha \right)} \right];{\gamma _{ij}}\} , $ | (4) |
式中, i=1, 2, …, n, n为评价指标数;tij(α)是支持α隶属度下界, fij(α)是从反对α的证据所导出的α非隶属度下界, γij为弃权者倾向于改投赞成票的可能性, 称为倾向性因子。
2) 计算Lij的满意度, 即估算Lij所表征的模糊隶属度, 得到其估算值为
| $ {L_{ij}}\left( \alpha \right) = {t_{ij}}\left( \alpha \right) + {\gamma _{ij}}\left[ {1 - {t_{ij}}\left( \alpha \right) - {f_{ij}}\left( \alpha \right)} \right]。$ | (5) |
3) 计算因素的基本权重。为了综合考虑专家的决策信息, 此处采用加权平均法:
| $ {\rho _i} = \sum\limits_{j = 1}^n {{L_{ij}}{\alpha _j}} /\sum\limits_{j = 1}^n {{L_{ij}}}。$ | (6) |
4) 对基本权重ρi进行归一化处理, 得到权重集K={k1, k2, …, kn}, 有
| $ {k_i} = \frac{{{\rho _i}}}{{\sum\limits_{i = 1}^n {{\rho _i}} }}。$ | (7) |
导致热时效过程中床身质量损失的原因是多方面的, 此处借鉴全面质量管理的“5M1E”分析法, 从人员、机器、材料、方法、测量、环境6个方面分析床身质量的损失情况, 并采用模糊综合评价等方法对其进行评价。各因素均在1至5分的范围内进行评定, 由于熵值越大代表所评定的因素越不稳定, 所以分值越低越好, 1分代表相应因素的最佳状况。
1.4.1 人员因素评价在热时效过程中:装炉、监控热处理过程、卸炉等都由人工完成, 人对热处理的效果影响较大。此处采用模糊综合评价法对人员因素进行评价, 参照文献[18]建立因素论域见表 1。
| 表 1 人因评价影响因素集 Table 1 Human factor evaluation set |
规程:操作规程和工作计划的科学性和实用性, 涉及正常作业、应急操作等。
培训:培训的质量和效果, 员工的知识、技能和经验水平等。
任务属性:工作负荷、任务特点、时间压力等。
身心状态:身体、心理、精神状态、警觉性、反应速度、疲劳程度等。
组织管理:工作组织效率, 监督管理效果等。
团队合作:团队成员的合作质量及团队之间的协作质量, 包括沟通与交流的效率、信任的水平、合作的氛围等。
建立因素论域后需要建立评语集, 建立评语集V={1, 2, 3, 4, 5}, 其中分值为1代表最佳状态。见表 2。
| 表 2 评语集 Table 2 Comment set |
建立因素集与评语集后即可组织相关专家对各项进行评分, 然后根据1.2节的模糊综合评价计算方法得出人因综合评价值x1。
1.4.2 机器因素评价热时效过程涉及的机器主要是热时效炉及其配套装置和起吊大件的起吊装置。热时效炉是进行热时效处理的主机, 确保其处在良好的状态下对时效过程极其重要。现在常用的热时效炉一般由炉体和电控两部分组成, 对炉体部分进行状态评估主要考虑其密封性、保温性以及炉内加热元件工作状态是否良好等;电控部分由温控和操作两部分组成, 温控部分主要评估交流接触器的工作状态及记录设备是否正常, 操作部分主要评估电器线路和控制系统工作状态是否良好。起吊装置主要考虑其能否平稳地进行床身等工件的运输, 因为剧烈的碰撞可能产生新的应力。结合以上各方面和平时的维护及修理信息对机器状态进行综合评判, 同样从1至5分进行赋值, 1代表机器处在极佳的状态, 得出对热时效过程参与机器的评价值x2。
1.4.3 材料因素评价热时效过程牵涉的材料很多, 但对处理效果有重要影响的材料主要是待处理的床身铸件、垫铁、热处理炉加热元件和热处理炉炉衬。床身铸件是由上一工序加工得到的, 热处理前需检查热处理工件表面有无影响热处理的潜在缺陷存在, 工件表面及隐蔽处是否清理干净, 是否存在影响热处理质量的杂物或污渍存在;垫铁用于多个零件一起时效时隔离零件, 垫铁应具有良好的热力学性能;时效炉的加热元件和炉衬是进行升温和保温最重要的部分, 其材料必须具备良好的性能以确保热处理工艺能够顺利实现。分别对以上4种材料进行评价, 估值1至5分, 取其平均值作为材料状态最终评价值x3。
1.4.4 方法因素评价方法因素可以说是对热时效过程质量损失影响很大的因素, 热时效工艺条件苛刻, 如温度高低, 时间长短, 温度速率等很多因素都会影响处理后的工件残余应力的消除效果, 如果操作不好, 就无法达到技术要求, 造成工件存在变形、开裂隐患。在热时效炉中, 工件装炉位置对残余应力消除情况也有影响。此处采用模糊综合评价对方法因素进行评判, 综合考虑以上因素的影响, 建立因素论域见表 3。
| 表 3 方法评价影响因素集 Table 3 Method evaluation set |
评语集同表 2, 组织相关专家对各项进行评分, 根据1.2的方法得出方法因素综合评价值x4。
1.4.5 测量因素评价热时效过程中炉内温度的测量结果是工序推行的基准, 因此保证温度测量的准确性对热时效的顺利进行有重大意义。现在的设备都是配备智能温度控制器进行温度控制, 其测量的准确度一般来讲还是比较高的, 主要是对温控系统的动态响应性能、控制精度和抗干扰能力进行评判。咨询相关专业人员得测量因素评价值x5。
1.4.6 环境因素评价所谓环境, 一般指生产现场的温度、湿度、粉尘或颗粒、噪音干扰、振动、照明、室内净化和现场污染程度等[19]。热时效过程中环境因素主要考虑以下几个方面:车间环境对工作人员工作状态的影响, 主要考虑空气质量、噪音和现场污染程度;堆放工件的地方的湿度和污染程度;时效炉安装位置的湿度和炉内的粉尘、颗粒等。综合考虑以上因素对环境因素评价得其评价值x6。
1.5 热时效下床身质量评价值的计算1) 计算各影响因素的熵值。
通过对各影响因素进行评价, 得到各自的状态评价值X={x1, x2, …, x6};对原始数据采用量纲一的方法进行标准化处理, 此处结合熵值的概念, 数值最小为优, 故以极小型指标类型进行处理, 计算式为
| $ X{'_i} = \frac{{{x_i} - \min {x_i}}}{{\max {x_i} - \min {x_i}}}, $ | (8) |
处理后的数据集合为
| $ X' = \{ x{'_i}\} , $ | (9) |
则ai的状态概率为
| $ {P_i} = x{'_i}/\sum\limits_{i = 1}^n {x{'_i}} , $ | (10) |
进而得出第i个影响因素的熵值为
| $ {H_i} = - \frac{1}{{\ln n}}{P_i}\ln {P_i}。$ | (11) |
2) 计算各影响因素的综合权重。
由熵值Hi可计算出第i个影响因素的熵权
| $ {w_i} = \frac{{1 - {H_i}}}{{n - \sum\limits_{i = 1}^n {{H_i}} }}。$ | (12) |
然后, 采用1.3节基于Vague集的模糊评判得到各影响因素的权重, 有权向量K={k1, k2, …, kn}。故第i个影响因素的综合权重为
| $ {\theta _i} = {k_i}{w_i}/\sum\limits_{i = 1}^n {{k_i}{w_i}} 。$ | (13) |
3) 计算综合评价熵值。
经过前面的计算可知各影响因素的评价值xi和综合权重θi, 则可计算综合评价值
| $ E = \sum\limits_{i = 1}^n {{x_i}{\theta _i}} 。$ | (14) |
根据得到的综合评价值可以对热时效下床身质量的状况进行判定, 结合熵的定义, 制定评价标准如表 4。
| 表 4 床身质量评价标准 Table 4 Standard for quality of lathe bed |
各影响因素的评价取值在1~5, 则综合评价熵值也在该区间;由于熵值越大, 质量损失越大, 可知综合评价值越接近5, 机床床身在热时效下的质量越差。
2 实例分析笔者以昆明机床股份有限公司某型号大型落地铣镗床的床身为研究对象, 对其热时效过程导致的床身质量损失进行评价。
2.1 热时效下床身质量各影响因素评价1) 人员因素评价。根据1.4.1节的内容, 组织厂内10个专家对6个影响因素进行评价, 得到模糊关系矩阵
| $ \mathit{\boldsymbol{R = }}\left[ {\begin{array}{*{20}{c}} {0.3}&{0.2}&{0.3}&{0.1}&{0.1}\\ {0.3}&{0.1}&{0.3}&{0.3}&{0.0}\\ {0.4}&{0.2}&{0.3}&{0.1}&{0.0}\\ {0.3}&{0.2}&{0.3}&{0.1}&{0.1}\\ {0.2}&{0.3}&{0.4}&{0.1}&{0.0}\\ {0.2}&{0.3}&{0.1}&{0.2}&{0.2} \end{array}} \right]。$ |
通过德尔菲法确定权向量A=(0.1, 0.3, 0.1, 0.2, 0.2, 0.1), 根据式(1)(2)得到
B=(0.28, 0.20, 0.30, 0.17, 0.05), 进一步根据式(3)有x1=2.51。
2) 机器因素评价。厂里热时效采用的是80 t零件人工热时效电阻炉, 运行情况正常。笔者邀请厂方专业的维护人员对人工电阻炉和梁式起吊设备进行评估, 给出了综合评价值x2=3.00。
3) 材料因素评价。通过实地调研, 发现热时效车间工作人员时效前未对床身铸件进行缺陷检查和杂物清理;热时效过程使用的垫铁性能良好, 能满足功能需求;人工热时效电阻炉的加热元件和内衬也能满足升温、保温的要求。结合以上分析, 对4种主要材料分别评分4, 2, 2, 3, 得出材料的综合评价值x3=2.75。
4) 方法因素评价。机床厂现行的大型床身热时效关键工艺如下:机床床身装炉时导轨向上平装;床身装于时效炉正中央温度最均匀的位置;支距过大时在中间加放垫铁, 垫铁间距不大于600 mm, 其与床身接触面的宽度不小于30 mm。床身铸件热时效的工艺流程见表 5。
| 表 5 床身热时效工艺流程 Table 5 The thermal aging process of lathe bed |
以现行工艺为基准, 组织厂里的工艺专家从表 3所示5个方面对其进行评估, 得到模糊关系矩阵
| $ \mathit{\boldsymbol{R }}_0=\left[ {\begin{array}{*{20}{c}} {0.4}&{0.2}&{0.2}&{0.1}&{0.1}\\ {0.5}&{0.2}&{0.2}&{0.1}&{0.0}\\ {0.4}&{0.3}&{0.1}&{0.2}&{0.0}\\ {0.3}&{0.2}&{0.1}&{0.2}&{0.2}\\ {0.6}&{0.3}&{0.1}&{0.0}&{0.0} \end{array}} \right]。$ |
运用德尔菲法确定的权重向量A0=(0.20, 0.25, 0.30, 0.15, 0.10), 依据式(1)~(3)得到工艺因素综合评价值x4=2.14。
5) 测量因素评价。采用厂方设备维护人员对温度控制系统的评价, 人工时效电阻炉配备的温控系统为行业普遍采用的设备, 经大量生产实践证明能够满足测量、控制要求。确定测量因素综合评价值x5=3.00。
6) 环境因素评价。经过对机床厂热时效车间的实地考察, 发现以下问题:车间灰尘大, 空气质量较差;工件堆放的位置较为潮湿;车间旁边是喷漆的地方, 异味较大;热时效车间离机加工车间和铸造车间很近, 噪音很大;车间内不少杂物无序堆放, 显得比较乱。综合以上分析, 确定环境因素的综合评价值x6=4.00。
2.2 综合评价值的计算通过2.1节分析计算得到各影响因素的评价集合X={2.51, 3.00, 2.75, 2.14, 3.00, 4.00};根据式(8)~(11)得到各因素的熵值H={0.113, 0.176, 0.148, 0.000, 0.176, 0.204};根据式(12)得到各因素的熵权W={0.171, 0.159, 0.164, 0.193, 0.159, 0.154}。
利用基于Vague集的模糊评判确定6个因素的权重, 进而结合熵权得到更客观的权重分配。首先设置评分标准, 此处设为5个等级, 按照重要程度标定分值1~5, 即α={α1, α2, α3, α4, α5}={1, 2, 3, 4, 5}, 分值越高代表其对热时效下的床身质量的影响越大。邀请厂方12位专家, 包括5位科研人员和7位技术人员, 参见公式(4)分别对各因素权重进行经验赋值, 以人员因素为例如下:β11={[0.15, 0.28];0.30};β12={[20.31, 0.52];0.65};β13={[0.30, 0.53];0.58};β14={[0.13, 0.39];0.41};β15={[0.11, 0.24];0.15}。
由公式(5)计算得
| $ L_1=\{0.1890, 0.4465, 0.4334, 0.2366, 0.1295\}。$ |
将L1代入公式(6)得评价因素基本权重ρ1=2.770 8, 同理可计算得到ρ2=3.021 4, ρ3=2.173 5, ρ4=3.661 9, ρ5=2.237 2, ρ6=1.894 2。根据式(7)对以上指标进行归一化处理得因素权重集
| $ \mathit{\boldsymbol{K}}=\{0.176, 0.192, 0.138, 0.232, 0.142, 0.120\}。$ |
根据式(13)计算得出综合权重:θ=(0.178, 0.181, 0.133, 0.265, 0.134, 0.109), 且有θ4>θ2>θ1>θ5>θ3>θ6。
得到综合权重后即可根据式(14)得出热时效下机床床身质量的综合评价值:E=2.761。参照表 4可认为床身热时效后质量水平为中等。厂方仍可以采取措施提高残余应力消除水平和床身质量。同时, 从综合权重的比较可以看出, 方法因素和机器因素是影响热时效过程下床身质量的最主要因素, 质量控制的方向是组织专业人员研究优化工艺规程和加强设备的维护管理, 同时评分最高(状况最差)的环境因素也应引起高度重视。
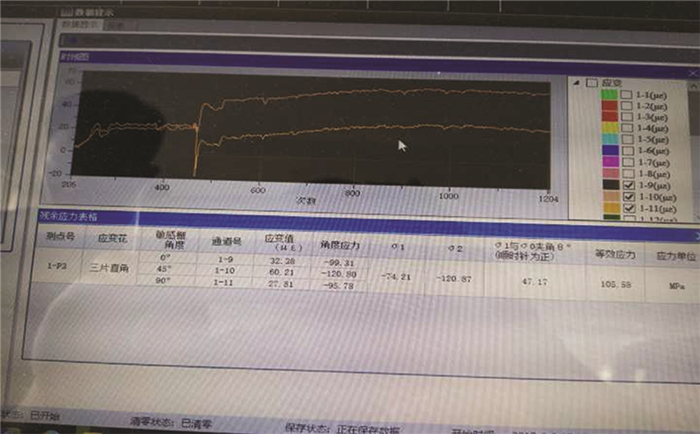
笔者所在的项目组在研究床身热时效效果的过程中, 采用Sigmar公司的仪器应用盲孔法对热时效前后床身的应力进行了测定(如图 1~3所示), 热时效前的状态为铸造完成后的状态。

|
图 1 应力测试现场 Figure 1 Stress test site |

|
图 2 钻孔后的应变片 Figure 2 Strain gauge after drilling |
|
图 3 Sigmar软件结果显示界面 Figure 3 Sigmar software results displayinterface |
测量时选取床身导轨面上9个典型的点位, 测量得到的等效应力值见表 6。
| 表 6 床身热时效前后等效应力比较 Table 6 Comparison of equivalent stress before and after the thermal aging of the bed |
为了便于对热时效后残余应力的消除情况进行评价, 参照床身质量评价标准(表 4)制定残余应力消除水平评价标准如表 7。
| 表 7 残余应力消除水平评价标准 Table 7 The evaluation criteria of residual stress elimination level |
残余应力的消除水平越高越好, 理想状态为百分之百消除;同时热时效过程中会产生新的应力, 存在热时效后应力水平高于热时效前的可能, 即这种情况下消除率为负, 属于残余应力消除水平很差的情况。
由表 6的数据计算得到该床身各测点残余应力的平均消除率为42%, 参照表 7的评价标准知残余应力消除水平为中等。
由于热时效过程影响床身质量水平的核心因素是残余应力消除水平, 所以可以把两者对应起来。通过前文的评价知两者均为中等水平, 证明本文热时效下的床身质量评价方法具有科学性和可信度。
3 结论笔者结合“热时效熵”与基于Vague集的模糊评判计算热时效下的机床床身质量综合评价值, 以昆明机床股份有限公司某型号大型落地铣镗床的床身为研究对象, 计算得出了该床身的质量综合评价值, 进而以评价结果为依据指导热时效工艺规程的改进。未来热时效下的零件质量评估研究可结合仿真软件的模拟, 综合评价、测量和模拟3个方面的结果确定评估值。
| [1] |
张根保, 张坤能.
残余应力消除技术[J]. 制造技术与机床, 2015(4): 6–11.
ZHANG Genbao, ZHANG Kunneng. Residual stress elimination technique[J]. Manufacturing Technology & Machine Tool, 2015(4): 6–11. (in Chinese) |
| [2] | Guney D. Residual stress analysis of insulation coatings for magnet technologies[J]. Archives of Metallurgy and Materials, 2013, 58(3): 673–676. DOI:10.2478/amm-2013-0053 |
| [3] |
吴晓明, 海燕, 邓雪莲.
重型机床基础结构件的热时效研究[J]. 现代机械, 2003(1): 57–58.
WU Xiaoming, HAI Yan, DENG Xuelian. Study on thermal aging of basic structural parts of heavy machine tools[J]. Modern Machinery, 2003(1): 57–58. (in Chinese) |
| [4] |
胡晓东.
振动时效与热时效消除铸造应力工艺比较[J]. 现代铸铁, 2009(6): 33–37.
HU Xiaodong. Comparison of vibration aging and thermal aging process to eliminate casting stress[J]. Modern Cast Iron, 2009(6): 33–37. (in Chinese) |
| [5] |
刘杨. 机床床身铸造及热时效过程残余应力研究[D]. 昆明: 昆明理工大学, 2016. LIU Yang. Study on residual stress of machine tool bed casting and thermal aging process[D]. Kunming: Kunming University of Science and Technology, 2016. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10674-1016230030.htm |
| [6] |
张明庆. 重型机床超长床身的制造工艺研究[D]. 长沙: 湖南大学, 2014. ZHANG Mingqing. Study on the manufacturing process of super long bed of heavy machine tool[J]. Changsha: Hunan University, 2014. (in Chinese) 重型机床超长床身的制造工艺研究 |
| [7] |
张根保, 庞继红, 陈国华, 等.
数控装备质量的模糊物元综合评价方法[J]. 重庆大学学报, 2011, 34(1): 36–41.
ZHANG Genbao, PANG Jihong, CHEN Guohua, et al. Numerical control equipment quality fuzzy matter-element comprehensive evaluation method[J]. Journal of Chongqing University, 2011, 34(1): 36–41. (in Chinese) |
| [8] | Singh A N, Moitra A, Bhaskar P, et al. Effect of thermal aging on microstructure, hardness, tensile and impact properties of alloy 617[J]. Materials Science & Engineering A, 2018, 710: 47–56. |
| [9] | Jeon J Y, Kim Y J, Kim J W, et al. Investigation of thermal aging effect on fracture toughness of cast stainless steels using experimental and numerical approach[J]. Procedia Engineering, 2015, 130: 820–827. DOI:10.1016/j.proeng.2015.12.200 |
| [10] | Shannon C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27(3): 379–423. DOI:10.1002/bltj.1948.27.issue-3 |
| [11] |
孟庆生. 信息论[M]. 西安: 西安交通大学出版社, 1986: 10-19.
MENG Qingsheng. Informationtheory[M]. Xian: Xian Jiaotong University Press, 1986: 10-19. (in Chinese) |
| [12] | He H J, An L, Liu W, et al. Prediction model of collapse risk based on information entropy and distance discriminant analysis method[J]. Mathematical Problems in Engineering, 2017(3): 1–8. |
| [13] |
王彬. 基于知识的机械产品概念设计过程防错理论与方法研究[D]. 北京: 北京航空航天大学, 2008. WANG Bin. Research on the theory and method of error prevention in conceptual design of mechanical products based on knowledge[D]. Beijing: Beihang University, 2008. (in Chinese) |
| [14] |
王新洲. 模糊空间信息处理[M]. 武汉: 武汉大学出版社, 2003: 178-189.
WANG Xinzou. Fuzzy spatialinformation processing[M]. Wuhan: Wuhan University Press, 2003: 178-189. (in Chinese) |
| [15] | Peng X Y, Bai X M. An investigation of Internet enterprise value assessment based on comprehensive evaluation method[J]. American Journal of Industrial and Business Management, 2017, 7(4): 501–512. DOI:10.4236/ajibm.2017.74036 |
| [16] | Elzarka H M, Yan H, Chakraborty D. A vague set fuzzy multi-attribute group decision-making model for selecting onsite renewable energy technologies for institutional owners of constructed facilities[J]. Sustainable Cities and Society, 2017, 35: 430–439. DOI:10.1016/j.scs.2017.08.025 |
| [17] |
张根保, 罗冬梅.
基于相对熵排序的装配序列质量模糊评价方法[J]. 中国机械工程, 2016, 27(8): 1089–1095.
ZHANG Genbao, LUO Dongmei. A fuzzy evaluation method of assembly sequence quality based on relative entropy sorting[J]. Chinese Mechanical Engineering, 2016, 27(8): 1089–1095. (in Chinese) |
| [18] |
柴松, 余建星, 杜尊峰, 等.
海洋工程人因可靠性定量分析方法与应用[J]. 天津大学学报, 2011, 44(10): 914–919.
CHAI Song, YU Jianxing, DU Zunfeng, et al. The method and application of reliability quantitative analysis formarine engineers[J]. Journal of Tianjin University, 2011, 44(10): 914–919. DOI:10.3969/j.issn.0493-2137.2011.10.012 (in Chinese) |
| [19] | Mcconnell K E, Bockstael N E. Chapter 14 Valuing the Environment as a Factor of Production[M]//Handbook of Environmental Economics. [S. l. ]: Elsevier B. V., 2005: 621-669. |
 2018, Vol. 41
2018, Vol. 41

