2. 铜仁学院 大数据学院, 贵州 铜仁 554300
2. School of Data Science, Tongren University, Tongren 554300, Guizhou, P. R. China
磁流化床在矿物分选、空气净化、生物转化等工业领域被广泛采用[1]。为了加强对颗粒运动的控制,磁流化床在普通流化床的基础上加入磁场,通过调整磁场的物性参数,控制磁流化床中颗粒的运动行为。在实际的工业应用中,磁流化床中的物料往往是潮湿的,或者为了增强物料的聚集行为,人为加湿。因此,研究磁场作用下磁性湿颗粒的运动机理具有重要意义。
离散元法(discrete element method, DEM)是一种被广泛使用的数值模拟颗粒运动的方法[2-4]。胡招文等[5]考虑静电力,采用DEM模拟研究了两种不同尺寸混合干颗粒粒径偏析分布规律。周恒等[6]采用DEM模拟填充床中的小颗粒渗流,研究了不同颗粒直径、阻尼系数以及滑动摩擦系数对小颗粒渗流行为的影响。文献[5-6]所针对的实际问题中,重力是颗粒运动的驱动力,而在流化床中,固相物料颗粒运动主要由流场驱动。通过动量交换实现流固耦合,Goniva等[7]研究了滚动摩擦对气动床中干颗粒运动行为的影响。
应该注意到,通过数值模拟研究流化床内湿颗粒的运动机理,需要考虑湿度对颗粒运动行为的影响。湿颗粒中,颗粒间存在液相,当两颗粒间液相积累到一定的程度,颗粒间会形成液桥。液桥会显著改变颗粒的受力情况,数值模拟中,湿度对颗粒运动行为的影响通过在颗粒动力学方程中加入液桥力模型体现[8-10]。Wang等[11]在颗粒运动方程中加入液桥力模型,对比干湿颗粒运动行为,定量分析了湿颗粒的聚集特性。Seah等[12]模拟了流化床中干湿颗粒运动,通过对比干湿颗粒的模拟结果,发现湿度加剧了颗粒聚团行为。Wang等[13]分别采用实验方法和数值模拟方法研究鼓泡床中湿颗粒的运动,其实验结果和数值模拟结果较为相符。与常规流化床不同,数值模拟磁流化床内磁性物料颗粒的运动,还应考虑磁场对磁性物料颗粒运动和分布的影响。磁场会改变磁性颗粒的受力,进而影响磁性颗粒的输运和分布。在数值模拟中通过在磁性颗粒的动力学方程中添加磁场力模型来体现磁场对磁性颗粒运动行为的影响[14-17]。以上对颗粒运动的数值模拟均得到了与实验较为相符的结果,为改进工业生产方法和提高生产效率提供了指导。然而,以上文献或者研究了无磁场作用下的湿颗粒运动,或者研究了磁场作用下干颗粒的运动行为,而对磁场作用下磁性湿颗粒的运动机理未进行研究。
笔者通过模拟2-D溃坝问题中湿颗粒的运动以及磁场作用下磁性湿颗粒的运动,研究匀强磁场作用下磁性湿颗粒的运动机理。颗粒运动采用DEM追踪,同时考虑颗粒碰撞、摩擦、湿度以及磁场对颗粒运动的影响。液桥力模型采用文献[18]所述模型,磁场力模型采用文献[19-20]所述模型。因为在溃坝问题中,颗粒运动的驱动力是重力,空气对颗粒的作用力远远小于其他作用力,所以数值模拟忽略气固相互作用对颗粒运动的影响。首先,通过改变颗粒的液体体积分数,研究了不同液体体积分数对颗粒运动的影响;其次,对比有磁场作用和没有磁场作用的湿颗粒的模拟结果,研究了匀强磁场作用下磁性湿颗粒的运动机理。
1 控制方程本文的数值模拟,对颗粒流动采用拉格朗日方法,用软球模型的离散元法[2]来模拟颗粒运动,磁性颗粒满足牛顿第二定律。
1.1 基于DEM的颗粒运动计算模型假设颗粒为球体,运动过程中颗粒无反应发生(即在整个计算过程中颗粒尺寸保持不变),在离散元法中颗粒的运动由牛顿第二运动定律表示为
| $ m\frac{{{{\rm{d}}^2}x}}{{{\rm{d}}{t^2}}} = {F_{\rm{c}}} + {F_{\rm{d}}} + {F_{\rm{m}}} + {F_{\rm{g}}}, $ | (1) |
| $ I\frac{{{\rm{d}}w}}{{{\rm{d}}t}} = T, $ | (2) |
式中:m和I分别表示颗粒的质量和惯性矩;w表示角速度;Fc、Fd、Fm和Fg分别是接触力、液桥力、磁场力和重力; T表示作用于颗粒合力力矩。
作用于颗粒的接触力Fc包括法向分量Fcn和切向分量Fct。基于Hertz理论[21],接触力的法向分量Fcn为
| $ {F_{{\rm{cn}}}} = \frac{4}{3}{E^*}{({R^*})^{1/2}}{\alpha ^{3/2}}, $ | (3) |
其中
| $ \Delta {F_{{\rm{cn}}}} = 2a{E^*}\Delta \alpha , $ | (4) |
其中
根据Mindlin-Deresiewicz理论[22],切向接触力增量可通过法向接触力增量计算,即
| $ \Delta {F_{{\rm{ct}}}} = 8a{G^*}{\theta _k}\Delta \delta + {\left( { - 1} \right)^k}\mu (1 - {\theta _k})\Delta {F_{cn}}, $ | (5) |
其中
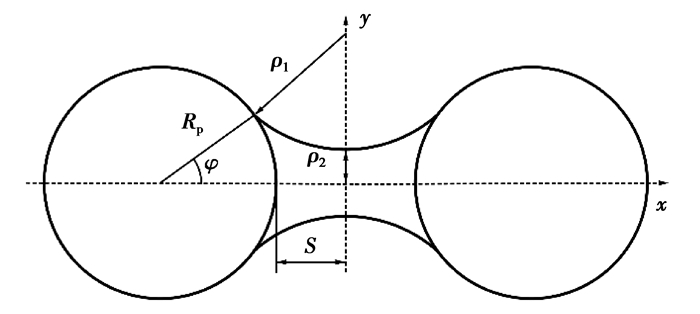
图 1为一致尺寸颗粒液桥示意图。图中Rp表示颗粒的半径;φ表示半填充角;S表示颗粒到桥颈的距离;ρ1表示液桥外弧面曲率半径,ρ2表示液桥内弧面曲率半径。依据文献[18],液桥力为
|
图 1 相同尺寸颗粒的液桥 Figure 1 The liquid bridge of same size particles |
| $ {F_{\rm{d}}} = 2{\rm{ \mathsf{ π} }}{\rho _2}{\sigma _{{\rm{lv}}}} + {\rm{ \mathsf{ π} }}\rho _2^2{\sigma _{{\rm{lv}}}}\left( {\frac{1}{{{\rho _1}}} - \frac{1}{{{\rho _2}}}} \right)。$ | (6) |
其中σlv为气液界面表面张力系数。
1.3 磁性颗粒受力模型磁场作用下,磁性颗粒受到的磁场力Fm包括磁场不均匀性引起的磁感应力Fme以及磁性颗粒诱导生产的磁场的不均匀性引起的磁感应力Fmi。依据Jackson的结论[20],Fme为
| $ {F_{{\rm{me}}}} = {V_{\rm{P}}}{\mu _0}{\chi _e}H\;\nabla H, $ | (7) |
Fmi包括径向力和偏向力。根据文献[19]所述,颗粒间的径向力为
| $ \begin{array}{l} {F_{\rm{r}}} = - \frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}}}\\ \left\{ {\frac{{{m^2}}}{{{r^3}}}\left[ { - 6\cos \left( {\theta - \gamma } \right)\sin \left( {\theta - \gamma } \right)} \right]{\gamma _r} + \left[ {1 - 3{{\cos }^2}\left( {\theta - \gamma } \right)} \right] - \left( {\frac{{3{m^2}}}{{{r^4}}} + \frac{{2m}}{{{r^3}}}{m_r}} \right)} \right\}, \end{array} $ | (8) |
| $ {\gamma _r} = - \frac{{9{\chi _{\rm{e}}}{V_{\rm{p}}}\sin 2\theta }}{{8{\rm{ \mathsf{ π} }}{r^4}\left\{ {{{\left[ {1 + \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\left( {3\cos 2\theta - 1} \right)} \right]}^2} + {{\left( {3\frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\sin 2\theta } \right)}^2}} \right\}}}, $ | (9) |
| $ \begin{array}{l} {m_{\rm{r}}} = \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}B}}{{{\mu _0}{{\left\{ {\cos \gamma - \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\left[ {\cos \gamma + 3\cos \left( {2\theta - \gamma } \right)} \right]} \right\}}^2}}} \times \\ \left\{ {\left[ {\left( {1 - \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}} \right)\sin \gamma + \frac{{3{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\sin \left( {2\theta - \gamma } \right)} \right]} \right.{\gamma _r} - \\ \left. {\;\;\;\;\;\;\;\;\frac{{3{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\left[ {\cos \gamma + 3\cos \left( {2\theta - \gamma } \right)} \right]} \right\}。\end{array} $ | (10) |
颗粒之间的偏向力为
| $ \begin{array}{l} {F_\theta } = - \frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}{r^4}}}\\ \left[ {6{m^2}\cos \left( {\theta - \gamma } \right)\sin \left( {\theta - \gamma } \right)(1 - {\gamma _\theta }) + 2m(1 - 3{{\cos }^2}\left( {\theta - \gamma } \right)){m_\theta }} \right], \end{array} $ | (11) |
| $ \begin{array}{l} {\gamma _\theta } = \frac{{2{{\left( {\frac{{3{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\sin 2\theta } \right)}^2}}}{{{{\left[ {1 + \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\left( {3\cos 2\theta - 1} \right)} \right]}^2} + {{\left( {\frac{{3{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\sin 2\theta } \right)}^2}}} + \\ \frac{{\frac{{6{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\cos 2\theta \left[ {1 + \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\left( {3\cos 2\theta - 1} \right)} \right]}}{{{{\left[ {1 + \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\left( {3\cos 2\theta - 1} \right)} \right]}^2} + {{\left( {\frac{{3{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\sin 2\theta } \right)}^2}}}, \end{array} $ | (12) |
| $ \begin{array}{l} \;\;\;\;{m_\theta } = \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}B}}{{{\mu _0}{{\left[ {\left( {1 - \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}} \right)\cos \gamma - 3\frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\cos \left( {2\theta - \gamma } \right)} \right]}^2}}} \times \\ \left\{ {\left[ {\left( {1 - \frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}} \right)\sin \gamma + 3\frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\sin \left( {2\theta - \gamma } \right)} \right]{\gamma _\theta } - 6\frac{{{\chi _{\rm{e}}}{V_{\rm{p}}}}}{{8{\rm{ \mathsf{ π} }}{r^3}}}\sin \left( {2\theta - \gamma } \right)} \right\}, \end{array} $ | (13) |
其中m为偶极矩,B为磁感应强度。
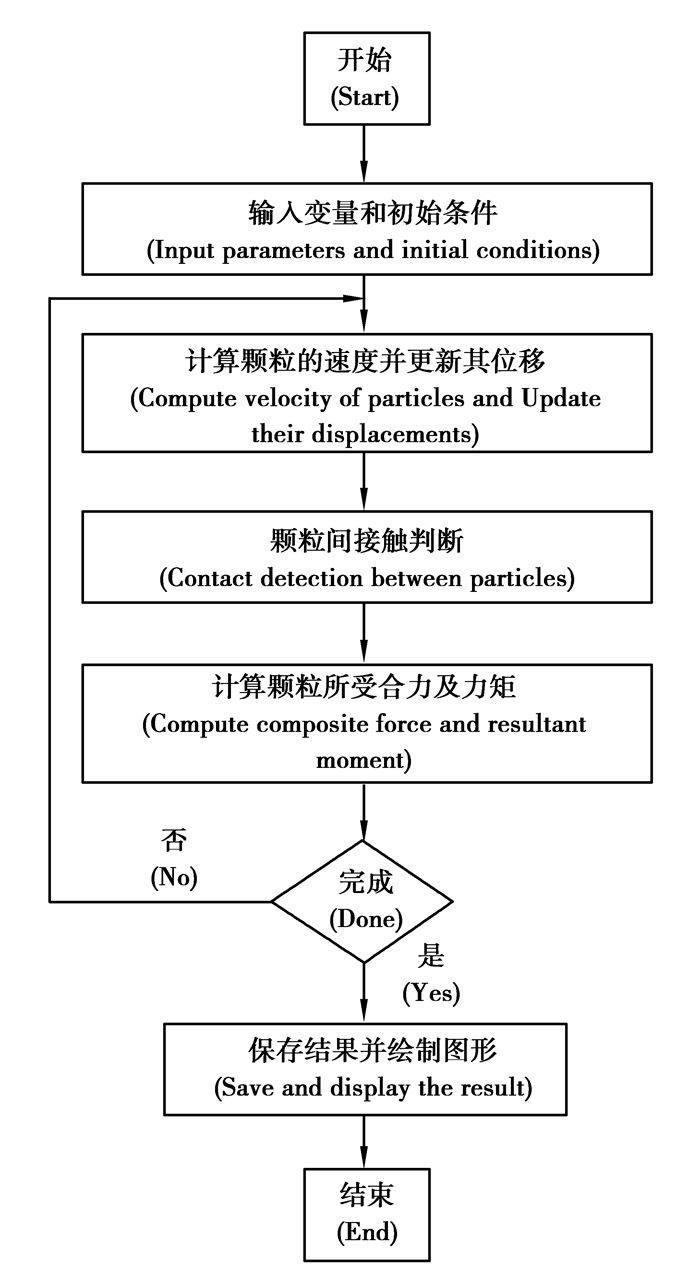
1.4 磁场影响下湿颗粒运动的DEM计算流程如图 2所示,DEM计算主要包含3个步骤:颗粒间的接触检测;颗粒的合力和力矩计算,包括接触力、液桥力和磁场力计算;计算颗粒在力作用下的运动。在接触检测阶段,除判断颗粒接触外,还需判断颗粒间是否存在液桥力。
|
图 2 DEM的计算流程 Figure 2 Flow chart of DEM |
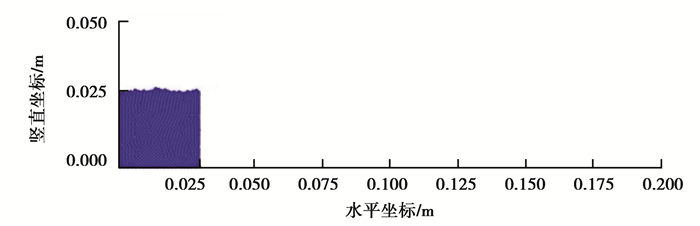
图 3表示2-D溃坝模型1 000个颗粒初始时刻的堆砌示意图,水平坐标0.200 m是箱体的长度,竖直坐标0.050 m表示箱体高度的一半。数值模型的物性参数如表 1所示,假设墙与颗粒是同样的材质。通过选取不同的液体体积分数,研究液体体积分数变化对颗粒运动行为的影响。液体体积分数Vf分别选取为0,0.1%,0.2%和0.4%。
|
图 3 初始时刻示意图 Figure 3 The configuration of particles at initial time |
| 表 1 颗粒和墙的物理参数 Table 1 Parameters of particles and wall |
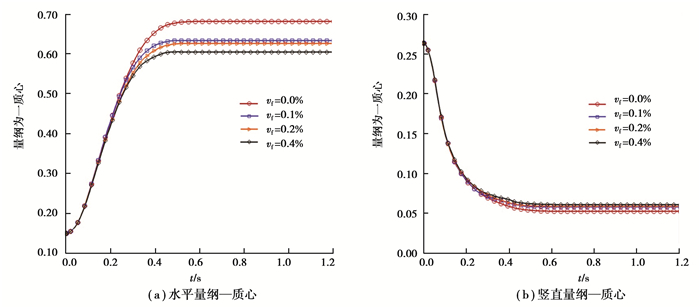
图 4(a)表示颗粒群水平量纲—质心,其值等于颗粒群质心水平坐标与箱体长度的一半的比值。图 4(b)表示颗粒群竖直量纲—质心,其值为颗粒群质心竖直坐标与箱体高度的比值。本文所有图中的时间都表示物理时间。
|
图 4 不同液体体积分数湿颗粒量纲一质心变化曲线 Figure 4 The change of centroidof wet particles with different liquid volume fraction |
第1阶段,颗粒在重力的驱动下质心快速变化,时间跨度为0~0.25 s。不同液体体积分数下质心差异不大。在颗粒运动的第1个阶段,重力是影响颗粒运的主导因素,液桥力是次要因素。
第2阶段,颗粒质心改变速度由快变缓,时间跨度为0.25~0.50 s。不同液体体积分数颗粒质心位移量在第2阶段出现明显差异,湿度对颗粒运动行为的影响主要发生在第2阶段。
第3阶段,颗粒质心不再变化。液体体积分数越低,颗粒运动质心位移越大。
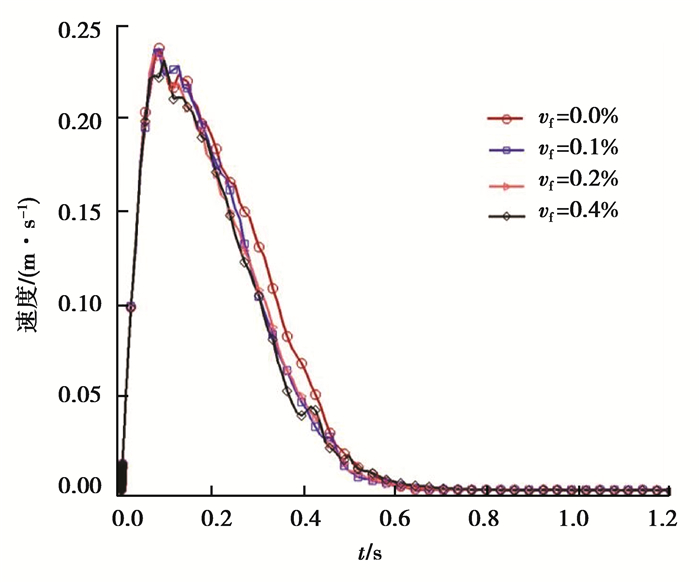
图 5表示不同液体体积分数下,颗粒的平均速度u与时间的关系。其中uxi和uyi分别表示颗粒i的水平速度分量和竖直速度分量;n表示颗粒群的粒子总数。平均速度u由式(14)(15)计算:
|
图 5 不同液体体积分数颗粒平均速度 Figure 5 The average velocityof wet particles with different liquid volume fraction |
| $ {u_i} = \sqrt {u_{xi}^2 + u_{yi}^2} ,i = 1,2, \cdots ,n $ | (14) |
| $ u = \frac{1}{n}\sum\limits_{i = 1}^n {{u_i}} 。$ | (15) |
颗粒平均速度的变化也分为3个阶段。
第1阶段,颗粒在重力的驱动下加速,时间跨度为0~0.08 s。不同液体体积分数颗粒平均速度差异不大,不同液体体积分数下颗粒平均速度的峰值与颗粒液体体积分数成反比。
第2阶段,颗粒平均速度减小,时间跨度为0.08~0.62 s。在该阶段的后半段(0.25~0.5 s这段时间),同一时刻,潮湿颗粒的平均速度比干颗粒的平均速度小。
第3阶段,颗粒运动停止的阶段。大致在0.7 s时刻,颗粒停止运动。
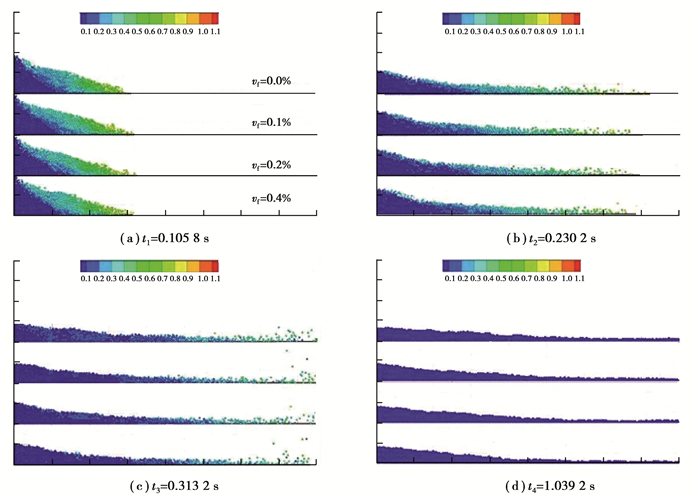
图 6为不同液体体积分数下颗粒在不同时刻的空间分布,图 6(a)对应的是颗粒在加速阶段的颗粒分布。大约在0.1 s时刻,干颗粒堆砌的高度已经明显下降,而湿颗粒堆的高度变化不大。与湿颗粒对比,干颗粒中的颗粒速度较大。图 6(b)中,随着液体体积分数增加,水平运动最远的颗粒的位移依次减小。图 6(b)和(c)两图中,与湿颗粒对比,干颗粒中的颗粒速度较大。图 6(d)是所有颗粒完全停止运动时的颗粒分布情况。运动停止时,干颗粒中较多颗粒运动到了箱体右侧,而湿颗粒中较多的颗粒堆积在箱体的左侧。
|
图 6 不同液体体积分数颗粒空间分布 Figure 6 The distribution of wet particles with different liquid volume fraction |
通过在湿颗粒的运动方程中增加磁场力模型,研究匀强磁场对湿颗粒运动行为的影响。数值模拟中,颗粒的液体体积分数是0.2%,匀强磁场的磁感应强度B=0.05 T,磁感线方向竖直向上。
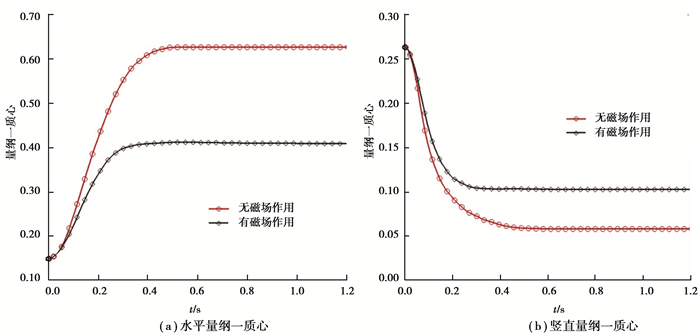
图 7(a)纵轴坐标含义与图 4(a)纵坐标含义相同,图 7(b)纵轴坐标含义与图 4(b)纵坐标含义相同。图 7显示,无磁场作用的湿颗粒大约在0.5 s时刻平均质心不再变化,而有磁场作用的颗粒大约在0.32 s时刻质心不再变化。从图 7中还可发现,无磁场作用的湿颗粒比有磁场作用的湿颗粒多做了相当于箱体长度1/10(箱体长度为0.2 m)的水平位移,无磁场作用的湿颗粒比有磁场作用的湿颗粒多做了相当于箱体高度1/20的竖直位移。
|
图 7 无磁场作用和有磁场作用的湿颗粒质心变化曲线 Figure 7 The centroid of wet particles with magnetic field and without magnetic field |
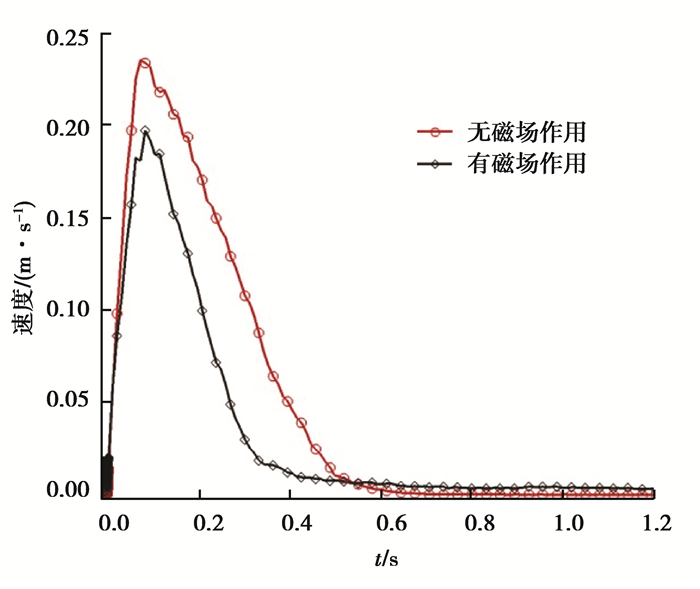
图 8颗粒的速度变化分为3个阶段:颗粒加速、颗粒减速和颗粒速度较平稳的阶段。
|
图 8 无磁场作用和有磁场作用的湿颗粒速度曲线 Figure 8 Average velocity of wet particles with magnetic field and without magnetic field |
颗粒加速阶段(0~0.08 s阶段),有磁场作用的湿颗粒速度增加得慢,说明磁场作用会阻碍颗粒速度增加,且有磁场作用的湿颗粒速度峰值比无磁场作用的湿颗粒速度峰值小。
颗粒减速阶段(0.08~0.51 s阶段),有磁场作用的湿颗粒的速度迅速减小,说明磁场作用导致了额外阻力。
速度平稳阶段(大约是0.51 s之后的阶段),颗粒速度趋于平稳后,速度不为0,且颗粒的速度有微小的波动。
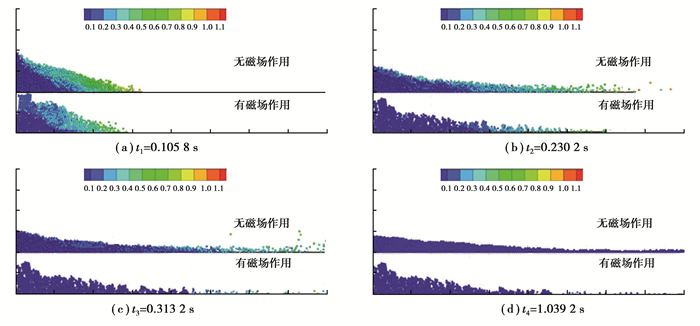
图 9中每个小图的上半部表示无磁场作用的湿颗粒的空间分布,下半部分表示有磁场作用下的湿颗粒的空间分布。
|
图 9 无磁场作用和有磁场作用的湿颗粒分布 Figure 9 Distribution of wet particles with magnetic field and without magnetic field |
1) 观察图 9(a)(b)和(c),可发现磁场作用下的湿颗粒运动的平均速度较低。
2) 观察图 9(b)(c)和(d),磁场作用下的湿颗粒平均位移量更小,较少的湿颗粒运动到了箱体的右侧。
3) 观察图 9,磁场使颗粒成链,颗粒链使箱体左侧的颗粒堆积形态在较短时间快速达到稳定状态,并且在堆积形态上,颗粒链使颗粒堆积错落,并出现较多的孔隙。
3 结论笔者通过改变颗粒的液体体积分数,研究了不同液体体积分数对颗粒运动的影响,发现随着液体体积分数增加,颗粒运动剧烈程度减弱,颗粒聚集行为增强。通过对比匀强磁场作用下和无磁场作用的湿颗粒的模拟结果,发现匀强磁场对湿颗粒运动主要产生以下几个方面的影响:
1) 匀强磁场使磁性湿颗粒成与磁感线方向平行的链,颗粒链对颗粒运动产生明显阻碍,一是颗粒链阻碍其左侧的颗粒向右侧运动,二是链中的颗粒被阻止从链中脱离。
2) 因颗粒链的阻碍,匀强磁场作用下的湿颗粒平均运动速度较低。
3) 因颗粒链的阻碍,存在匀强磁场作用下的湿颗粒平均位移量较小,只有少量的颗粒运动到了箱体右侧。
4) 因为颗粒成链,运动停止时,绝大多数颗粒以链状堆积在箱体的左侧,其最终形态为颗粒堆有较多的孔隙。
| [1] |
曾平, 周涛, 陈冠群, 等.
磁场流化床的研究与应用[J]. 化工进展, 2006, 25(4): 371–377.
ZENG Ping, ZHOU Tao, CHEN Guanqun, et al. Research and application of magnetic fluidized bed[J]. Chemical Industry and Engineering Progree, 2006, 25(4): 371–377. (in Chinese) |
| [2] | Cundall P A, Strack O D L. A discrete numerical mode for granular assemblies[J]. Géotechnique, 1979, 29(1): 47–65. DOI:10.1680/geot.1979.29.1.47 |
| [3] | Liu M, Wen Y, Liu R, et al. Investigation of fluidization behavior of high density particle in spouted bed using CFD-DEM coupling method[J]. Powder Technology, 2015, 280: 72–82. DOI:10.1016/j.powtec.2015.04.042 |
| [4] | Yamamoto M, Ishihara S, Kano J. Evaluation of particle density effect for mixing behavior in a rotating drum mixer by DEM simulation[J]. Advanced Powder Technology, 2016, 27(3): 864–870. DOI:10.1016/j.apt.2015.12.013 |
| [5] |
胡招文, 郭福亮, 陈晨, 等.
DEM模拟解析二元混合颗粒粒径偏析分布规律[J]. 重庆大学学报, 2015, 38(5): 38–45.
HU Zhaowen, GUO Fuliang, CHEN Chen, et al. Analysis on distribution law of particle size segregation of binary particle mixtures based on DEM[J]. Journal of Chongqing University, 2015, 38(5): 38–45. DOI:10.11835/j.issn.1000-582X.2015.05.006 (in Chinese) |
| [6] |
周恒, 张涛, 游洋, 等.
填充床中细小颗粒渗流行为的DEM模拟[J]. 重庆大学学报, 2015, 38(5): 59–65.
ZHOU Heng, ZHANG Tao, YOU Yang, et al. Analyses on percolation behavior of small particles in a packed bed by DEM[J]. Journal of Chongqing University, 2015, 38(5): 59–65. DOI:10.11835/j.issn.1000-582X.2015.05.009 (in Chinese) |
| [7] | Goniva C, Kloss C, Deen N G, et al. Influence of rolling friction on single spout fluidized bed simulation[J]. Particuology, 2012, 10(5): 582–591. DOI:10.1016/j.partic.2012.05.002 |
| [8] | He Y, Peng W, Tang T, et al. DEM numerical simulation of wet cohesive particles in a spout fluid bed[J]. Advanced Powder Technology, 2016, 27(1): 93–104. DOI:10.1016/j.apt.2015.10.022 |
| [9] | Tsunazawa Y, Fujihashi D, Fukui S, et al. Contact force model including the liquid-bridge force for wet-particle simulation using the discrete element method[J]. Advanced Powder Technology, 2016, 27(2): 652–660. DOI:10.1016/j.apt.2016.02.021 |
| [10] | Tang T, He Y, Tai T, et al. DEM numerical investigation of wet particle flow behaviors in multiple-spout fluidized beds[J]. Chemical Engineering Science, 2017, 172: 79–99. DOI:10.1016/j.ces.2017.06.025 |
| [11] | Wang M, Zhu W, Sun Q, et al. A DEM simulation of dry and wet particle flow behaviors in riser[J]. Powder Technology, 2014, 267: 221–233. DOI:10.1016/j.powtec.2014.07.026 |
| [12] | Seah S L L, Lim E W C. Density segregation of dry and wet granular mixtures in gas fluidized beds[J]. Aiche Journal, 2015, 61(12): 4069–4086. DOI:10.1002/aic.v61.12 |
| [13] | Wang T, He Y, Tang T, et al. Experimental and numerical study on a bubbling fluidized bed with wet particles[J]. Aiche Journal, 2016, 62(6): 1970–1985. DOI:10.1002/aic.15195 |
| [14] | Hao Z, Xiang L, Lu H, et al. Numerical simulation of particle motion in a gradient magnetically assisted fluidized bed[J]. Powder Technology, 2010, 203(3): 555–564. DOI:10.1016/j.powtec.2010.06.022 |
| [15] | Soda R, Takagi K, Ozaki K. Extended particle-based simulation for magnetic-aligned compaction of hard magnetic particles[J]. Journal of Magnetism and Magnetic Materials, 2015, 396: 128–134. DOI:10.1016/j.jmmm.2015.08.018 |
| [16] | Soda R, Takagi K, Ozaki K. Numerical simulation of magnetic-aligned compaction with pulsed high magnetic field[J]. Scripta Materialia, 2016, 120: 41–44. DOI:10.1016/j.scriptamat.2016.04.028 |
| [17] | Higashida K, Rai K, Yoshimori W, et al. Dynamic vertical forces working on a large object floating in gas-fluidized bed:discrete particle simulation and Lagrangian measurement[J]. Chemical Engineering Science, 2016, 151: 105–115. DOI:10.1016/j.ces.2016.05.023 |
| [18] | Chena Y, Zhaoa Y, Gaob H. Liquid bridge force between two unequal-sized spheres or a sphere and a plane[J]. Particuology, 2011, 9(4): 374–380. DOI:10.1016/j.partic.2010.11.006 |
| [19] | Jovanovic G N, Sornchamni T, Atwater J E, et al. Magnetically assisted liquid-solid fluidization in normal and microgravity conditions:experiment and theory[J]. Powder Technology, 2004, 148(2/3): 80–91. |
| [20] | Jackson J D. Classical Electrodynamics[M]. New York: John Willey and Sons, Inc, 1999. |
| [21] | Johnson K L. Contact Mechanics[M]. Canbridge: Cambridge University Press, 1987. |
| [22] | Mindlin R D, Deresiewicz H. Elastic spheres in contact under varying oblique forces[J]. J. Appl. Mech.Asme, 1953, 20(3): 327–344. |
 2018, Vol. 41
2018, Vol. 41


