可靠性是决定产品功能能否正常实现的重要指标,并突出表现在产品服役的经济性和寿命等方面。复杂机电产品的可靠性增长和优化一直是个备受瞩目的问题,因此,对机电产品的可靠性优化研究非常有必要。在产品的可靠性评估和优化中,可靠性建模发挥着重要作用[1]。常用的可靠性模型构建方法有可靠性框图法[2]、FTA分析法[3], 以及马尔科夫链建模[4]等。Gurov[5]和Perez-Ocon[6]利用马尔科夫链模型对可修系统进行了可靠性建模并预测了系统的可靠度;Bourouni[7]、Hajeeh[8]利用FTA分析法对反向过滤器可靠性进行了评价, 结果证明,利用FTA建模后优化的结果更为理想。上述可靠性建模方法常用于简单的系统建模,但针对复杂的系统或概念不明确的灰色系统,往往很难据此构造确切的数学表达式。张根保等[9-10]从机电产品的基本运动功能出发,将运动功能逐层分解到零部件的元动作,作为可靠性分析的模型,并运用于故障诊断和装配过程的可靠性控制。但这些文献都只是从一个维度提出系统的分解思路,并未建立可靠性分析的数学模型,无法解决在费用成本约束下的可靠性优化问题。
优化模型建立以后,通常利用某种算法对其进行求解,常见的求解方法有GA优化算法和PSO优化算法等。Bhunia[11]利用GA算法对系统可靠性进行了区间优化,取得了较好的效果;Shakerian[12]通过对GA算法进行改进, 使得交叉概率和变异概率随适应度自动变换, 加快了算法的搜索效率,并在径向分布系统的可靠性优化中取得了明显效果;Coelho[13]利用PSO分别对串联、并联系统的可靠性进行了优化,从而证明了PSO优化算法的有效性;Huang[14]通过对粒子的更新方法进行优化, 并把改进后的PSO应用于系统可靠性优化分配中,结果表明改进PSO算法的优化效果明显优于基本粒子群算法。上述启发式的优化算法[15]都是使用单一或改进的算法进行问题求解,虽然取得了一定效果,但存在算法易陷入局部最优解、收敛过快、后期运算效率下降[16]的问题。
针对上述方法在构造复杂系统可靠性数学模型时存在的问题,笔者在文献[9-10]的基础上,进一步研究了基于功能分解后系统的可靠性优化模型构造。从机电产品的基本运动功能出发,通过对各元动作单元的可能故障及原因进行分析,建立了系统的可靠性优化数学模型。在模型求解上充分利用GA算法可以同时评价搜索空间中的多个适应度值、算法易于实现的优点,并配合PSO的局部寻优能力,然后通过链接整合的方法实现GA-PSO算法联动,形成混合GA-PSO算法。将混合GA-PSO算法应用于数控磨齿机的可靠性优化上,简化了系统可靠性数学建模过程,使优化目标更加具有针对性,并取得了很好的效果。
1 FMA-FTA的可靠性优化模型构建对复杂机电产品进行结构分解常用的思路有“Top-Down”方式,即自上而下将系统分解成相对简单的子系统、部件、组件[17]。传统的故障树分析法都是基于这种研究思路对功能部件进行故障及原因追溯的,但这种分析方法并未与产品运动功能、零部件的运动联系起来。另外,许多复杂机电产品主要元器件是机械结构件,在设计之初并没有进行冗余设计或设置代替工作模式,这也是区别于电子产品的主要特征之一[18]。因此,从任务过程上来说,复杂机电产品是一个多功能的串联系统,其功能过程的基本动作都是该串联系统的独立组成单元,任何一个动作故障都会导致其功能失效,故从功能运动的角度研究其故障逻辑,其可靠性模型明显变得简单。
1.1 FMA功能分解概述FMA功能分解是指将整机按“功能—运动—动作”的逻辑顺序进行分解,把系统功能分解成不可再分的动作组合,其中不可再分的动作称之为元动作,由实现该元动作的所有组成零件称为元动作单元。FMA功能分解方法的核心思想就是将机电产品工作过程中的复杂运动拆分成一系列基本的动作单元,在此基础上对元动作进行故障分析并提出控制策略。传统的系统分解思路是按CAP(部件—组件—零件)的硬件组成关系进行,其最终研究对象是零部件,而FMA分解法则是针对系统功能进行分解,明显更具有针对性。图 1是对机电产品分别进行CAP和FMA分解的比较。

|
图 1 系统分解的过程 Figure 1 Process of system decomposing |
故障树一般用于产品质量改进,针对产品在使用过程中出现的故障进行建树,而元动作的故障模式都是根据设计要求推导出来,实际过程中可能发生,也可能不发生。因此,元动作故障树分析既要利用故障树分析思路,又要在过程中体现元动作故障模式的特点,基于FMA模型的可靠性建模过程如下:
1) 确定顶事件,绘制元动作故障树。在对机床进行FMA分解后,通过FMECA分析元动作的故障模式及其影响,确定所有元动作的关键故障模式A*,其中A*为向量{A1*, A2*, …, An*},在此基础上以各关键元动作故障模式为顶事件,利用FTA逻辑门将各顶事件分解至基本事件X,其中X为向量组{x1, x2, x3, …, xk},图 2是选取某一元动作单元故障Ah*建立的故障树。
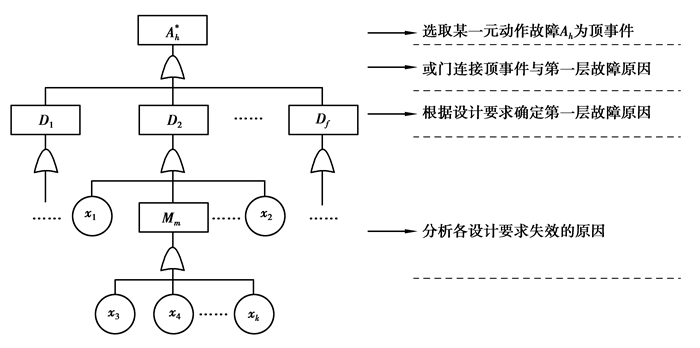
|
图 2 元动作故障树的建立 Figure 2 Process of action fault tree |
2) 故障树定性分析。通过对树进行逻辑简化,求得导致顶事件发生的最小割集。
3) 顶事件概率计算。设xl和φl分别表示底事件和顶事件的状态变量,且取值为0(底事件或顶事件不发生)和1(底事件或顶事件发生)2种状态。由于顶事件的发生状态取决于底事件,且一般机械系统的故障树最小割集就是底事件本身,因此,文中故障树的分析对象为最小割集,故定义:
| $ \mathit{\boldsymbol{A}}_h^ * = \varphi \left( X \right) = \bigcup\limits_{i = 1}^{{k_h}} {{x_i}} , $ | (1) |
| $ \begin{array}{*{20}{c}} {p\left( {A_h^ * } \right) = p\left( {\bigcup\limits_{i = 1}^{{k_h}} {{x_i}} } \right) = p\left( {{x_1} \cup {x_2} \cup \cdots \cup {x_{{k_h}}}} \right) = }\\ {\sum\limits_{i = 1}^{{k_h}} {p\left( {{x_i}} \right)} - \sum\limits_{i < j = 2}^{{k_h}} {p\left( {{x_i}{x_j}} \right)} + \sum\limits_{i < j < l}^{{k_h}} {p\left( {{x_i}{x_j}{x_l}} \right)} - \cdots + {{\left( { - 1} \right)}^{{k_h} - 1}}p\left( {{x_1}{x_2} \cdots {x_{{k_h}}}} \right)。} \end{array} $ | (2) |
在实际运用过程中,一般忽略掉三次项[19],可得顶事件近似计算值
| $ p\left( {A_h^ * } \right) = \sum\limits_{i = 1}^{{k_h}} {p\left( {{x_i}} \right)} - \sum\limits_{i < j = 2}^{{k_h}} {p\left( {{x_i}{x_j}} \right)} , $ | (3) |
式中:kh为系统第h个元动作所对应的底事件总数;p(xi)表基本事件xi发生的概率;p(xixj)表示共因事件的发生概率。
4) 系统故障概率函数。从功能过程上来说,机电产品是一个多动作的串联系统,组成功能的基本动作都是该串联系统的独立组成单元,任何一个动作故障都会导致其功能失效,且元动作故障树的各底事件两两互不相交。因此,根据系统的FMA-FTA分解树可以构建系统功能过程的故障概率函数
| $ p\left( S \right) = \sum\limits_{h = 1}^n {\sum\limits_{i = 1}^{{k_h}} {p\left( {x_i^h} \right)} } , $ | (4) |
式中:n为系统按功能分解后的元动作总数;p(xih)为系统第h个元动作所对应的第i个底事件发生的概率;kh为系统第h个元动作所对应的底事件总数。
1.3 系统可靠性费用函数产品的可靠性与其费用息息相关[20], 需将两者综合考虑,既要保证产品满足使用者的要求, 又要能使其投入费用最低,这就是费用与可靠性的优化问题。费用函数表示了可靠性与费用之间的关系,包含了提高单元可靠性所花费的各种人力、物力、财力总和。各元动作设计单元的可靠性费用与其故障概率密切相关,故障概率越低,可靠性费用越高。借鉴文献[21-22]中的方法,构造元动作设计单元的可靠性费用函数
| $ C\left( {x_i^h} \right) = {\alpha _i}{\left( {\frac{{ - t}}{{\ln \left[ {1 - p\left( {x_i^h} \right)} \right]}}} \right)^{{\beta _i}}},i = 1,2, \cdots ,{k_h};h = 1,2, \cdots ,n, $ | (5) |
式中:αi和βi为元动作单元i的可靠性成本函数曲线的尺度和形状因子,用来描述曲线特征;t为元动作设计单元的无故障运行时间;kh为系统第h个元动作所对应的底事件总数;p(xih)为系统的第h个元动作所对应的第i个底事件的故障概率。
系统的可靠性费用是各个元动作设计单元的可靠性费用的总和,因此,整个系统的可靠性费用
| $ C = \sum\limits_{i = 1}^{{k_h}} {\sum\limits_{h = 1}^n {{\alpha _h}{{\left( {\frac{{ - t}}{{\ln \left[ {1 - p\left( {x_i^h} \right)} \right]}}} \right)}^{{\beta _h}}}} } 。$ | (6) |
在式(5)和式(8)所示的故障概率函数和可靠性费用函数的基础上,以系统故障概率最小为目标函数,可靠性费用为约束条件,构造出基于FMA故障树的可靠性优化模型
| $ \left. \begin{array}{l} \min p\left( S \right) = \sum\limits_{h = 1}^n {\sum\limits_{i = 1}^{{k_h}} {p\left( {x_i^h} \right)} } \\ {\rm{s}}.{\rm{t}}.C = \sum\limits_{i = 1}^{{k_h}} {\sum\limits_{h = 1}^n {{\alpha _h}\left( {\frac{{ - t}}{{\ln \left[ {1 - p\left( {x_i^h} \right)} \right]}}} \right){\beta _h} - {C_0}} } \le 0\\ 0 < p\left( {x_i^h} \right) < 1 \end{array} \right\}。$ | (7) |
1) GA算法
GA算法是通过模仿生物界的进化规律总结出来的一种最优化方法。由美国的J. Holland教授1975年最先提出[23]。其主要特点是对优化目标函数没有连续、可导的限制,且具有很好的全局寻优特性,标准的遗传算法主要包括种群初始化、交叉、变异和寻优比较,直到满足收敛条件。
2) PSO算法
PSO算法是一种模仿鸟群和鱼群觅食的群智能算法,由Kennedy等[24]于1995年首次提出,该算法和GA算法类似,都是通过对群体迭代进行寻优求解,但它没有交叉、变异的处理过程,也不需要调整很多参数,由于其简单易实现而受到广大学者和工程人员的关注。假设在某个D维的搜索空间上,种群Xi=(xi1, xi1, , …xiD)T由M个粒子组成, 其中每个问题的可能解由对应粒子在D维搜索空间中的位置进行表达。第i个粒子的速度为Vi=(vi1, vi1, , …viD)T,其个体极值为Pi=(pi1, pi1, , …piD)T,种群的群体极值为Pg=(pg1, pg1, , …pgD)T,种群的适应度值则可以根据粒子所在位置进行计算。
在每次迭代过程中,粒子通过个体极值和群体极值更新自身的速度和位置,即
| $ {v^{k + 1id}} = v_{id}^k + {c_1}{r_1}\left( {p_{id}^k - x_{id}^k} \right) + {c_2}{r_2}\left( {p_{gd}^k - x_{gd}^k} \right), $ | (8) |
| $ {x^{k + 1id}} = x_{id}^k + {v_{\left( {k + 1} \right)id}}, $ | (9) |
式中:d=1, 2, …, D; i=1, 2, …, M; k表示目前的总迭代次数;Vid表示第i个粒子的飞行速度;c1为非负常数,称为加速因子;r1是分布于[0, 1]区间的随机数。为避免粒子在空间中盲目搜索,一般给粒子的位置和速度设置为[-xmax, xmax]的限制区间。
传统的PSO算法虽然全局寻优能力强,算法也简单易实现,但是在搜索后期容易出现因粒子趋同现象,可能导致求解目标值存在较大的偏差。
2.2 混合PSO算法为了改善传统优化算法的不足,文中提出GA-PSO混合算法:1)算法运行初期,通过把随机选出的M个粒子的当前位置、个体极值,以及按适应度值排序后的M个个体极值进行交叉、变异,得到新的种群。如果新位置的适应值优于排序后对应的历史最优适应值,则用新的适应值取代历史最优适应度值,同时更新粒子位置。显然,这样的交叉和变异使得粒子在每次进化中同时利用了自己和种群中优良个体的经验信息,增加了粒子的多样性,扩大了搜索范围,从而增加了种群的进化质量,使粒子找到全局最优的可能性增大,避免算法过早收敛于局部最优解;2)在算法运行后期,通过PSO算法优异的局部寻优能力进行更加精细化的局部搜索,从而加快算法收敛速度,找到最优极值点。通过遗传算法对种群的个体极值和群体极值进行交叉、变异处理,不仅把遗传算法的全局寻优能力与粒子群算法的局部寻优能力结合起来,也加快了算法的进化速度,同时避免了算法陷入局部最优或过早收敛的现象。混合PSO算法的具体步骤如下,算法流程如图 3所示。

|
图 3 GA-PSO算法流程图 Figure 3 Algorithm flowchart of GA-PSO |
Num.1种群初始化。根据实际问题对种群的规模M、变异概率Pm、交叉概率Pc,以及最大迭代次数N进行初始化赋值,产生初始种群pop1,给出惯性权重ω,c1,c2。
Num.2种群更新。求出初始种群pop中全部个体的适应度值,并计算个体极值Pi和群体极值Pg,按式(9)、式(10)对粒子的速度和位置进行更新,得到新的种群pop0。
Num.3交叉操作。从新种群pop0中按轮盘赌选择算子选出M个个体,并以交叉概率Pc两两进行交叉操作,得到种群pop1。
Num.4变异操作。从pop1中继续按轮盘赌选择算子选出M个个体,并以变异概率Pm依次对个体进行变异,得到新种群pop2。
Num.5选择操作。利用精英算子从pop1和pop2中选出M个个体组成下一代种群pop,同时更新全局最优极值Pg。
Num.6结果判断。假如满足最大迭代次数或最优个体所对应的网络输出误差满足精度要求,程序停止;否则,转向Num.2。
3 应用以某机床厂型号为YK7236A的高精度数控磨齿机为例,针对齿轮磨削加工过程,对整机功能进行FMA分解,如图 4所示。从图 4中可以对整个磨削过程中运动的传递方式进行分析,并将整个功能分解成主运动和辅助运动。

|
图 4 YK7236A磨削加工FMA分解图 Figure 4 Decomposing diagram of YK7236 |
1) 主运动系:Cp={M1}={A1→A2→A3},其中“→”是元动作间的连接符,用来表示动作间的先后逻辑关系以及动作之间的串联关系。其中,砂轮主轴是由功率电机直接带动,没有齿轮变速传动,所以电机转动、主轴转动及砂轮转动就是组成主运动的元动作。因此,从主运动的动作分解中可以发现,虽然按照“功能—运动—动作”的流程,但并不是每个运动、每个功能都严格具有这3个层次,应该根据部件具体结构具体分析。
2) 辅助运动系:Xp={M2, M3, M4, M5},其中F2负责砂轮对刀运动,并控制砂轮的吃刀量,F3用于在加工斜齿时保证齿坯与砂轮正确啮合,F4用于控制砂轮磨削时的进给量,F5用于控制砂轮进行连续磨削。从图 4中可以得出各个辅助运动间的运动逻辑关系
| $ {M_2} = \left( {{A_4} \to {M_2} - 1 \to {A_5}} \right) = \left( {{A_4} \to {A_{12}} \to {A_{13}} \to {A_{14}} \to {A_5}} \right), $ |
| $ {M_3} = \left( {{A_6} \to {M_3} - 1 \to {A_7}} \right) = \left( {{A_6} \to {A_{15}} \to {A_{16}} \to {A_{17}} \to {A_7}} \right), $ |
| $ {M_4} = \left( {{A_8} \to {A_9}} \right), $ |
| $ {M_5} = \left( {{A_{10}} \to {M_{5 - 1}} \to {M_{5 - 2}} \to {M_{5 - 3}} \to {A_{11}}} \right) = \\\left( {{A_{10}} \to {A_{18}} \to {A_{19}} \to {A_{20}} \to {A_{21}} \to {A_{22}} \to {A_{23}} \to {A_{24}} \to {A_{11}}} \right)。$ |
FMA分解后,通过功能FMECA分析得到了各元动作故障模式,并通过危害性分析获取影响磨齿机磨削过程各元动作的关键故障模式:{A1*, A2*, …, A24*}。考虑到元动作单元的固有质量主要取决于设计,且上述元动作失效对系统的危害性较大,因此,本例针对这24个元动作关键故障模式进行FTA分析,并建立基于元动作故障的系统加工过程的可靠性优化数学模型。模型建立如下:
假设各元动作故障模式只有发生和不发生2种状态,系统磨削加工只有故障和正常2种状态。由FTA分析可知,各元动作故障模式两两互不相关,设各元动作故障模式的故障概率为p(y1), p(y2), …, p(y24),系统加工过程的故障概率函数为p(S),根据磨齿机磨削过程的故障机理以及式(5)构建系统加工过程的故障概率函数
| $ p\left( S \right) = 1 - \prod\limits_{i = 1}^{24} {\left[ {1 - p\left( {{y_i}} \right)} \right]} 。$ | (10) |
根据式(8)可构造可靠性费用函数
| $ C = \sum\limits_{i = 1}^{24} {{\alpha _i}{{\left( {\frac{{ - t}}{{\ln \left[ {1 - p\left( {{y_i}} \right)} \right]}}} \right)}^{{\beta _i}}}} , $ | (11) |
其中:t=600 h, β1=β2=…=β24=1.5,α1=α2=…=α24=4.45×10-5,取C0=350,联合式(10)、式(11)可得系统的可靠性优化模型
| $ \left\{ \begin{array}{l} p\left( S \right) = 1 - \prod\limits_{i = 1}^{24} {\left[ {1 - p\left( {{y_i}} \right)} \right]} ,\\ C = \sum\limits_{i = 1}^{24} {{\alpha _i}{{\left( {\frac{{ - t}}{{\ln \left[ {1 - p\left( {{y_i}} \right)} \right]}}} \right)}^{{\beta _i}}}} - 350 \le 0,\\ 0 < p\left( {{y_i}} \right) < 1,i = 1,2, \cdots ,24。\end{array} \right. $ | (12) |
文中分别选取了GA算法、PSO算法以及混合GA-PSO算法对磨齿机的可靠性函数进行了优化求解。为验证混合GA-PSO算法的优化性能,分别与GA算法优化、PSO算法优化进行对比,设置3种优化算法的最大迭代次数为200,其他参数设置见表 1。
| 表 1 参数设置表 Table 1 Parameter setting |
通过MATLAB运行各算法,得到的参数优化结果见表 2。
| 表 2 优化结果 Table 2 Optimization result |
上述优化结果表明:在同样的可靠性投入费用约束下,GA算法、PSO算法运行时间分别为3.087 4 s和1.076 5 s,混合GA-PSO算法运行时间为2.429 1 s。表面上看,混合GA-PSO算法的运行时间居中,但是结合最终优化结果来看,混合PSO算法优化求解得到的系统失效概率最小。综上所述,混合GA-PSO算法在较短的运行时间内搜索能力更强、结果更优。
4 结论1) 通过提出以故障概率替代可靠度、结合FMA-FTA故障树来构造系统任务过程的故障概率函数,从元动作单元出发对系统的可靠性进行优化的方法,拓宽了复杂机电产品的可靠性优化思路, 使优化更具有针对性;
2) 将GA有约束非线性算法与PSO算法有约束非线性算法进行了比较,在分析了单独算法的局限后提出将二者算法有机结合。通过对PSO算法引入交叉和变异操作增强了粒子群优化算法的全局寻优能力,加快了算法的进化速度,提高了收敛精度;
3) 通过对数控磨齿机进行仿真分析,结果证明,混合GA-PSO算法的优化结果更为理想,针对故障率较大的元动作故障模式可以为工程设计人员提供改进方向,从而提高复杂机电产品的固有可靠性水平。
| [1] |
Ridwan M I, Yen K L, Musa I A, et al. Reliability and availability assessment of transmission overhead line protection system using reliability block diagram[C]//IEEE International Conference on Power and Energy, Kuala Lumpur, Malaysia: IEEE, 2010: 964-969. http://www.researchgate.net/publication/251986657_Reliability_and_availability_assessment_of_transmission_overhead_line_protection_system_using_reliability_block_diagram
|
| [2] |
Li H, Liu S, Cong M. Reliability estimation based on moving average and state space model for rolling element bearing[J]. International Journal of Performability Engineering, 2015, 11(3): 243-256. |
| [3] |
Ramabhotla S, Bayne S, Giesselmann M. Reliability optimization using fault tree analysis in the grid connected mode of microgrid[C]//Green Technologies Conference, April 6-8, 2016, Kansas City, MO, USA: IEEE, 2016: 136-141. http://www.researchgate.net/publication/301800526_Reliability_Optimization_Using_Fault_Tree_Analysis_in_the_Grid_Connected_Mode_of_Microgrid
|
| [4] |
Kharchenko V, Butenko V, Odarushchenko O, et al. Markov's modeling of NPP I & C reliability and safety: Optimization of Tool-and-Technique selection[C]//Second International Symposium on Stochastic MODELS in Reliability Engineering, Life Science and Operations Management, February 15-18, 2016. Beer-Sheva, Israel: IEEE, 2016: 328-336. http://ieeexplore.ieee.org/document/7433136/
|
| [5] |
Gurov S V, Utkin L V. A new method to compute reliability of repairable m-out-of-n systems by arbitrary distributions[J]. Microelectronics Reliability, 1995, 34(12): 1877-1889. |
| [6] |
Perez-Ocon R, Montoro-Cazorla D. Transient analysis of a repairable system, using phase-type distributions and geometric processes[J]. IEEE Transactions on Reliability, 2004, 53(2): 185-192. DOI:10.1109/TR.2004.829145 |
| [7] |
Bourouni K. Availability assessment of a reverse osmosis plant:comparison between reliability block diagram and fault tree analysis methods[J]. Desalination, 2013, 313(7): 66-76. |
| [8] |
Hajeeh M, Chaudhuri D. Reliability and availability assessment of reverse osmosis[J]. Desalination, 2000, 130(2): 185-192. DOI:10.1016/S0011-9164(00)00086-2 |
| [9] |
张根保, 王新, 冉琰, 等. 复杂机电产品基于元动作分解的可靠性建模及故障诊断[J]. 重庆大学学报, 2017, 40(8): 9-18. ZHANG Genbao, WANG Xin, RAN Yan, et al. Reliability modeling and fault diagnosing method of complex electromechanical products based on meta[J]. Journal of Chongqing University, 2017, 40(8): 9-18. (in Chinese) |
| [10] |
张根保, 葛红玉, 刘佳, 等. 可靠性驱动的装配过程建模及预测方法[J]. 计算机集成制造系统, 2012, 18(2): 349-355. ZHANG Genbao, GE Hongyu, LIU Jia, et al. Assembly process and perdition method of reliability-driven[J]. Computer Integrated Manufacturing Systems, 2012, 18(2): 349-355. (in Chinese) |
| [11] |
Bhunia A K, Sahoo L. Genetic algorithm based reliability optimization in Interval environment[J]. Computers & Industrial Engineering, 2011, 62(1): 152-160. |
| [12] |
Shakerian R, Tavakkolaii H, Kamali S H, et al. Improved genetic algorithm for loss and simultaneously reliability optimization in radial distribution systems[C]//International Conference on Advanced Computer Theory and Engineering.[S.l.]: IEEE, 2010: V4-325-V4-329. http://ieeexplore.ieee.org/document/5579500/
|
| [13] |
Coelho L D S. An efficient particle swarm approach for mixed-integer programming in reliability-redundancy optimization applications[J]. Reliability Engineering & System Safety, 2009, 94(4): 830-837. |
| [14] |
Huang C L, Yeh W C. Simplified Swarm Optimization Algorithm for reliability redundancy allocation problems[C]//Telecommunication Networks and Applications Conference, Sydney, NSW, Australia: IEEE, 2015: 1-4. http://ieeexplore.ieee.org/document/7366780/
|
| [15] |
Kuo W, Wan R. Recent advances in optimal reliability allocation[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A:Systems and Humans, 2007, 37(2): 143-156. DOI:10.1109/TSMCA.2006.889476 |
| [16] |
Shi X H, Lu Y H, Zhou C G, et al. Hybrid evolutionary algorithms based on PSO and GA[C]//Evolutionary Computation, 2003. Congress on Evolutionary Computation, Canberra, ACT, Australia: IEEE, 2003, 4: 2393-2399. http://www.researchgate.net/publication/4074678_Hybrid_evolutionary_algorithms_based_on_PSO_and_GA
|
| [17] |
Zhang G B, Lou J H, Li D Y, et al. Fault diagnosis study of complex mechanism based on FMA function decomposition model[J]. Procedia Cirp, 2015, 27: 176-180. DOI:10.1016/j.procir.2015.04.062 |
| [18] |
张根保, 张恒, 范秀君, 等. 数控机床基于FMA的功能分解与可靠性分析[J]. 机械科学与技术, 2012, 31(4): 528-533. ZHANG Genbao, ZHANG Heng, FAN Xiujun, et al. Function decomposition and reliability analysis of CNC machine using function-motion-action[J]. Mechanical Science and Technology, 2012, 31(4): 528-533. (in Chinese) |
| [19] |
龚庆祥. 型号可靠性工程手册[M]. 北京: 国防工业出版社, 2007. GONG Qingxiang. Model reliability engineering manual[M]. Beijing: National Defense Industry Press, 2007. |
| [20] |
Jiang Z, Zhou T, Zhang H, et al. Reliability and cost optimization for remanufacturing process planning[J]. Journal of Cleaner Production, 2016, 135(4): 1602-1610. |
| [21] |
Wu P, Gao L, Zou D, et al. An improved particle swarm optimization algorithm for reliability problems[J]. Isa Transactions, 2011, 50(1): 71-81. DOI:10.1016/j.isatra.2010.08.005 |
| [22] |
Garg H. An approach for solving constrained reliability-redundancy allocation problems using cuckoo search algorithm[J]. Beni-Suef University Journal of Basic and Applied Sciences, 2015, 4(1): 14-25. DOI:10.1016/j.bjbas.2015.02.003 |
| [23] |
余胜威. MATLAB优化算法案例分析与应用[M]. 北京: 清华大学出版社, 2015. YU Shengwei. Case analysis and application of matlab optimization algorithm[M]. Beijing: Tsinghua University Press, 2015. |
| [24] |
Kennedy, Erbthart R C. Particle swarm optimization[C]//IEEE International Conference on Neural Networks. Perth, WA, Australia: IEEE, 1995: 1942-1948.
|
 2018, Vol. 41
2018, Vol. 41

