2. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044
2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China
近年来,风力发电产业发展迅速,电网中风电装机容量大幅增加[1]。直驱永磁同步发电机(PMSG, permanent magnet synchronous generator)凭借无齿轮箱、低电压穿越能力强等优点逐渐兴起,与双馈感应发电机(DFIG, doubly-fed induction generator)一起成为风电机组的主流机型。大容量风电场的建设具有分期特点,不同时期风电机组的类型常根据当期建设成本和技术水平等因素灵活选择,由此形成不同机组混合运行的局面[2]。目前,DFIG和PMSG是混合风电场的两种主力机组。
DFIG和PMSG的运行原理与传统同步发电机差异较大。DFIG需要电力电子变流器提供转子励磁,而PMSG则由变流器提供并网接口。电力电子器件的引入,使得风电机组与传统同步发电机的短路电流在成分、衰减时间等特征上有较大区别[3],风电机组的大量接入可能导致原有保护的误动或拒动,影响系统安全运行。作为发展多年的主流风电机组,DFIG已积累了相对丰富的研究成果,其建模方法和控制策略已比较成熟[4]。已有文献对于不同的故障类型[5-7]、Crowbar是否动作[8-9]等情况下定子短路电流的特征及计算进行了分析,文献[10]则考虑了转子控制对机组暂态特性的影响。
风电场具有集群网络化的特点,尽管DFIG单机故障分析得到了越来越多的关注,但是却鲜有文献考虑多机相互影响下DFIG的故障特性。文献[11]研究了双馈风电场馈线的短路电流特性,但未考虑风电场与单个DFIG故障特性的差异。文献[12]采用了分群聚合的方法来计算混合风电场短路电流,但未考虑机组间的相互影响。DFIG定子绕组直接连到电网,对系统参数和运行工况等敏感[13]。在DFIG与PMSG共同构成的混合风电场中,不同机组实施不同的故障穿越策略,将导致机组暂态特征的多样化,这可能影响并联运行的DFIG的暂态过程。目前风电场暂态分析主要采用机组直接并联和容量加权来实现机群模型简化[14-15],未考虑机组相互影响造成的单机暂态特征变化,这将影响风电场机组的分群和聚合,不利于风电场整体短路电流的准确计算。
笔者以电网对称故障时混合风电场中DFIG的短路电流特征为对象,基于DFIG与PMSG的模型及控制方式,推导了DFIG和PMSG的单机短路电流工频分量表达式,进而建立了多机并联运行时风场等值模型,通过多机并联运行时DFIG工频短路电流表达式分析了多机相互影响下DFIG工频短路电流与单独接入时的区别,对多机并联运行下DFIG工频短路电流的影响因素及其变化规律进行了分析和总结,并通过仿真验证了分析的正确性。
1 DFIG及其暂态过程在同步旋转坐标系下,DFIG的定转子电压矢量方程和磁链矢量方程可以表示为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{u}}_{{\rm{s\_D}}}} = {R_{{\rm{s\_D}}}}{\mathit{\boldsymbol{i}}_{{\rm{s\_D}}}} + \frac{{{\rm{d}}{\mathit{\boldsymbol{\psi }}_{{\rm{s\_D}}}}}}{{dt}} + j{\omega _{\rm{s}}}{\mathit{\boldsymbol{\psi }}_{{\rm{s\_D}}}},\\ {\mathit{\boldsymbol{u}}_{{\rm{r\_D}}}} = {R_{{\rm{r\_D}}}}{\mathit{\boldsymbol{i}}_{{\rm{r\_D}}}} + \frac{{{\rm{d}}{\mathit{\boldsymbol{\psi }}_{{\rm{r\_D}}}}}}{{dt}} + j{\omega _{\rm{p}}}{\mathit{\boldsymbol{\psi }}_{{\rm{r\_D}}}}, \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\psi }}_{{\rm{s\_D}}}} = {L_{{\rm{s\_D}}}}{\mathit{\boldsymbol{i}}_{{\rm{s\_D}}}} + {L_{{\rm{m\_D}}}}{\mathit{\boldsymbol{i}}_{{\rm{r\_D}}}},\\ {\mathit{\boldsymbol{\psi }}_{{\rm{r\_D}}}} = {L_{{\rm{m\_D}}}}{\mathit{\boldsymbol{i}}_{{\rm{s\_D}}}} + {L_{{\rm{r\_D}}}}{\mathit{\boldsymbol{i}}_{{\rm{r\_D}}}}, \end{array} \right. $ | (2) |
式中:下标D表示DFIG机组;u、i、ψ分别表示电压、电流、磁链矢量,所有电气量均归算到定子侧;ωp为转差角速度,等于同步角速度ωs与转子角速度ωr之差;Rs_D、Rr_D分别为定转子电阻;Ls_D、Lr_D、Lm_D分别为定子电感、转子电感和激磁电感。
电网发生故障后,由式(2)可得DFIG定子短路电流
| $ {\mathit{\boldsymbol{i}}_{{\rm{sf\_D}}}} = \frac{1}{{{L_{{\rm{s\_D}}}}}}{\mathit{\boldsymbol{\psi }}_{{\rm{sf\_D}}}} - \frac{{{L_{{\rm{m\_D}}}}}}{{{L_{{\rm{s\_D}}}}}}{\mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}}, $ | (3) |
式中,下标f表示故障后的电气量。
通常配电网继电保护通过检测短路电流工频分量实现动作,因此,主要分析DFIG定子短路电流工频分量。由式(3)可知,DFIG定子短路电流工频分量取决于定子磁链工频分量ψsf_Dfu和转子电流工频分量irf_Dfu,上标fu表示工频分量。定子磁链工频分量由DFIG端电压决定,可表示为
| $ \mathit{\boldsymbol{\psi }}_{{\rm{sf\_D}}}^{{\rm{fu}}} = \frac{{{\mathit{\boldsymbol{u}}_{{\rm{sf\_D}}}}}}{{j{\omega _{\rm{s}}}}}, $ | (4) |
式中:usf_D=kus0_D为故障后忽略相位跳变的DFIG机端电压,us0_D为故障前的机端电压,k为机端电压跌落的比例。
转子短路电流工频分量根据故障情况的不同可分为2种情况:1)严重故障时Crowbar动作,此时转子电流由转子绕组磁链的暂态过程所决定;2)非严重故障时转子侧变流器(RSC, rotor-side converter)保持对转子绕组的控制,此时转子电流由转子绕组磁链磁链的暂态过程和RSC共同控制。
外部电网严重故障时,转子绕组Crowbar动作短接转子绕组,同时闭锁RSC,此时电压方程中urf_D=0。式(2)消去定子电流并代入转子电压方程,可得转子电流的一阶微分方程,其特解即为工频分量
| $ \mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}^{{\rm{fu}}} = - \frac{{s{L_{{\rm{m\_D}}}}{\mathit{\boldsymbol{u}}_{{\rm{sf\_D}}}}}}{{{L_{{\rm{s\_D}}}}\left( {{R_{{\rm{rc\_D}}}} + j\sigma {\omega _{\rm{p}}}{L_{{\rm{r\_D}}}}} \right)}}, $ | (5) |
式中:s为转差率;σ=1-Lm_D2/(Lr_DLs_D),为漏感系数;Rrc_D为转子电阻Rr_D和Crowbar电阻Rc_D之和。
外部电网非严重故障时,RSC保持调控作用,其内环电流控制方程为
| $ \mathit{\boldsymbol{u}}_{{\rm{rf\_D}}}^ * = {k_{{\rm{rp}}}}\left( {\mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}^ * - {\mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}}} \right) + {k_{{\rm{ri}}}}\int {\left( {\mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}^ * - {\mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}}} \right){\rm{d}}t} + j{\omega _{\rm{s}}}\sigma {L_{{\rm{r\_D}}}}{\mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}}, $ | (6) |
式中:urf_D*、irf_D*分别表示RSC输出电压参考值和电流参考值;krp、kri分别为RSC电流内环比例和积分系数;上标*表示参考值。
认为变流器能理想跟踪调制波,即urf_D=urf_D*,联立式(1)和式(6)可得转子电流的二阶微分方程,其特解即为转子电流工频分量[16],有
| $ \mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}^{{\rm{fu}}} = \mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}^ * 。$ | (7) |
转子电流参考值可根据外环功率参考值得到
| $ \mathit{\boldsymbol{i}}_{{\rm{rf\_D}}}^ * = \frac{{{\psi _{{\rm{sf\_D}}}}}}{{{L_{{\rm{m\_D}}}}}} - \frac{{{L_{{\rm{s\_D}}}}}}{{{L_{{\rm{m\_D}}}}}}\frac{{{{\mathit{\boldsymbol{\tilde S}}}^ * }}}{{{\mathit{\boldsymbol{u}}_{{\rm{sf\_D}}}}}}, $ | (8) |
式中,
故DFIG定子工频短路电流可表示为
| $ \mathit{\boldsymbol{i}}_{{\rm{sf\_D}}}^{{\rm{fu}}} = \left\{ {\begin{array}{*{20}{c}} {\frac{{{\mathit{\boldsymbol{u}}_{{\rm{sf\_D}}}}}}{{{Z_{\rm{e}}}}},{\rm{Crowbar}}\;动作,}\\ {\frac{{{{\mathit{\boldsymbol{\tilde S}}}^ * }}}{{{\mathit{\boldsymbol{u}}_{{\rm{sf\_D}}}}}},{\rm{Crowbar}}\;不动作,} \end{array}} \right. $ | (9) |
式中,
PMSG作为变流器接口电源,在电网故障时,变流器隔离故障点和发电机。因此,PMSG的故障特性主要由网侧变流器决定[17]。PMSG的网侧变流器与DFIG采用相同的控制策略。忽略外环参考值过渡过程,并认为变流器输出实际值ugf_P能很好地跟踪参考值ugf_P*,此时PMSG短路电流仅取决于电流内环的动态。当电流内环根据典型Ⅰ型系统设计参数时,具有非常快的响应速度,短路电流的衰减分量时间常数非常大,因此,可认为短路后直接过渡到短路稳态[18],即PMSG工频短路电流为
| $ {\mathit{\boldsymbol{i}}_{{\rm{gf\_P}}}} = \mathit{\boldsymbol{i}}_{{\rm{gf\_P}}}^ * 。$ | (10) |
风电并网国家标准GB/T 19963-2011要求,系统发生三相短路时,风电场注入系统的无功电流为
| $ {I_{\rm{Q}}} \ge {K_{\rm{d}}}\left( {0.9 - {U_{\rm{g}}}} \right),0.2{\rm{p}}.{\rm{u}}. \le {U_{\rm{g}}} \le 0.9{\rm{p}}.{\rm{u}}., $ | (11) |
式中:IQ为无功电流标幺值; Ug为电网电压标幺值;Kd为无功增益系数,Kd≥1.5。
当PMSG按此要求进行故障穿越时,优先输出无功功率,再决定有功电流的参考值。此时,对网侧变流器的内环电流参考值有
| $ \left\{ {\begin{array}{*{20}{c}} {i_{{\rm{gfq\_P}}}^ * \ge {K_{\rm{d}}}\left( {0.9 - {U_{\rm{g}}}} \right),}\\ {i_{{\rm{gfq\_P}}}^ * = \min \left( {\sqrt {i_{{\rm{gmax}}}^2 - i_{{\rm{gfq\_P}}}^{ * 2}} ,i_{{\rm{g0d\_P}}}^ * } \right),} \end{array}} \right. $ | (12) |
式中igmax为GSC允许输出电流的最大值。
3 混合风电场中DFIG短路电流推导根据DFIG定子工频短路电流表达式,当Crowbar动作时,DFIG可等值为一负阻抗;当Crowbar不动作时,DFIG可等值为一受控电流源。其单机并网工频等值电流如图 1所示。
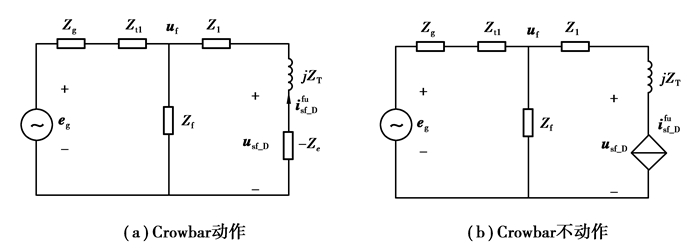
|
图 1 输电线三相短路下DFIG单机工频等值电路图 Figure 1 Fundamental-frequency equivalent circuit of single DFIG under three-phase short-circuit in transmission line |
对于PMSG,由式(11)可知,电网对称故障后PMSG输出的短路电流为一定值工频电流,可等效为恒流源,则PMSG单机在输电线三相短路下的工频等值电路图如图 2所示。
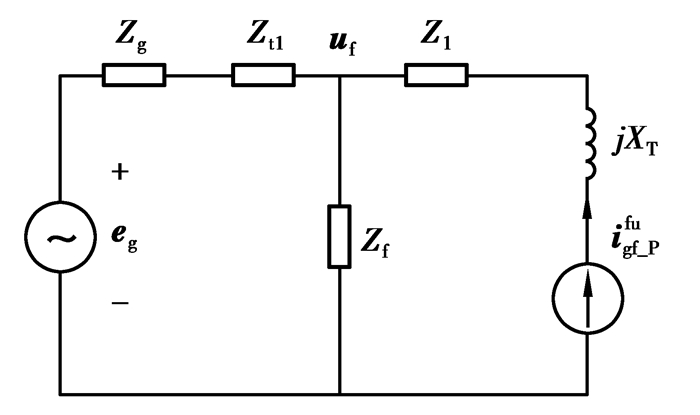
|
图 2 输电线三相短路下PMSG单机工频等值电路图 Figure 2 Fundamental-frequency equivalent circuit of single PMSG under three-phase short-circuit in transmission line |
风电场通常采用链式连接方式,多台风机通过对应的升压变压器连接到一条馈线上,多条馈线再汇集到更高电压等级的母线上。同一馈线上多台风机并联运行,对于整个风电场多条馈线仍满足并联关系。对于2条馈线,1条多台DFIG并联运行、1条多台PMSG并联运行时,电网故障后的工频等值电路图如图 3所示。其中,同类型机组参数相同,DFIG与PMSG额定容量、交流侧额定电压相同。

|
图 3 多机并联运行工频等值电路图 Figure 3 Fundamental-frequency equivalent circuit of multiple turbines in parallel |
由于馈线阻抗相较于变压器电抗和归算至馈线电压等级的DFIG暂态电抗很小,为计算简便,忽略馈线阻抗的影响。图 3中当2条馈线分别接入m1台DFIG和m2台PMSG时,以接在点N1处的DFIG为1号机组,则1号DFIG工频短路电流为
| $ \mathit{\boldsymbol{i}}_{{\rm{sf\_D1}}}^{\left( {{\rm{m1}},{\rm{m2}}} \right)} = \left\{ \begin{array}{l} - \frac{{{m_2}{Z_{\rm{G}}}i_{{\rm{gf\_P}}}^{{\rm{fu}}} + {e_g}}}{{\frac{{{Z_{\rm{D}}}{Z_{\rm{G}}}}}{{{Z_{\rm{f}}}}} + {m_1}{Z_{\rm{G}}} + {Z_{\rm{D}}}}},{\rm{Crowbar}}\;动作,\\ \frac{{{\mathit{\boldsymbol{u}}_{{\rm{m2}}}} - {m_2}{Z_{\rm{G}}}\mathit{\boldsymbol{i}}_{{\rm{gf\_P}}}^{{\rm{fu}}} - {e_g}}}{{2{m_1}{Z_{\rm{G}}}}},{\rm{Crowbar}}\;不动作, \end{array} \right. $ | (13) |
式中:
多机并联运行时将对1号DFIG产生暂态相互影响,从式(13)中可以看出,这种相互影响主要与机组数量、DFIG和PMSG的故障穿越方式、故障严重程度等因素有关。
4.1 机组数量由式(13)可知,Crowbar动作和不动作时DFIG机组数越大,1号DFIG工频短路电流越小。Crowbar动作时,PMSG机组数越大,1号DFIG工频短路电流越大;Crowbar不动作时,PMSG机组数越多,1号DFIG工频短路电流越小。由此可知,多机并联运行下1号DFIG的工频短路电流相比单机运行时将发生变化,1号DFIG单独接入时的短路电流为
| $ \mathit{\boldsymbol{i}}_{{\rm{sf\_D1}}}^{\left( 1 \right)} = \left\{ {\begin{array}{*{20}{c}} { - \frac{{{\mathit{\boldsymbol{e}}_{\rm{g}}}}}{{\frac{{{Z_{\rm{D}}}{Z_{\rm{G}}}}}{{{Z_{\rm{f}}}}} + {Z_{\rm{G}}} + {Z_{\rm{D}}}}},{\rm{Crowbar}}\;动作,}\\ {\frac{{{\mathit{\boldsymbol{u}}_0} - {\mathit{\boldsymbol{e}}_{\rm{g}}}}}{{2{Z_{\rm{G}}}}},{\rm{Crowbar}}\;不动作,} \end{array}} \right. $ | (14) |
式中,
1号DFIG多机同时接入与单独接入时相比工频短路电流增量为
| $ \Delta {\mathit{\boldsymbol{i}}_{{\rm{sf\_D1}}}} = \mathit{\boldsymbol{i}}_{{\rm{sf\_D1}}}^{\left( {{\rm{m1,m2}}} \right)} - \mathit{\boldsymbol{i}}_{{\rm{sf\_D1}}}^{\left( {\rm{1}} \right)} = \left\{ \begin{array}{l} \frac{{\left( {{m_1} - 1} \right){Z_{\rm{G}}}{\mathit{\boldsymbol{e}}_{\rm{g}}} - {m_2}{Z_{\rm{G}}}\left( {\frac{{{Z_{\rm{D}}}{Z_{\rm{G}}}}}{{{Z_{\rm{t}}}}} + {Z_{\rm{G}}} + {Z_{\rm{D}}}} \right)\mathit{\boldsymbol{i}}_{{\rm{gf\_P}}}^{{\rm{fu}}}}}{{\left( {\frac{{{Z_{\rm{D}}}{Z_{\rm{G}}}}}{{{Z_{\rm{t}}}}} + {m_1}{Z_{\rm{G}}} + {Z_{\rm{D}}}} \right)\left( {\frac{{{Z_{\rm{D}}}{Z_{\rm{G}}}}}{{{Z_{\rm{t}}}}} + {Z_{\rm{G}}} + {Z_{\rm{D}}}} \right)}},{\rm{Crowbar}}\;动作,\\ \frac{{{\mathit{\boldsymbol{u}}_{{\rm{m2}}}} + \left( {{m_1} - 1} \right){Z_{\rm{G}}}{\mathit{\boldsymbol{e}}_{\rm{g}}} - {m_1}{\mathit{\boldsymbol{u}}_0} - {m_2}{Z_{\rm{G}}}\mathit{\boldsymbol{i}}_{{\rm{gf\_P}}}^{{\rm{fu}}}}}{{2{m_1}{Z_{\rm{G}}}}},{\rm{Crowbar}}\;不动作。\end{array} \right. $ | (15) |
由式(15)可知,该增量与机组数量有关,其随机组数量的变化规律与1号DFIG在多机并联情况下的短路电流随机组数量的变化规律相同。由于各DFIG机组短路电流相同,m1台混合风电场中的DFIG工频短路电流相对m1倍单台DFIG接入时的工频短路电流的增量可表示为Δisf_Dsum=m1Δisf_D1。该表达式可用于修正传统单机短路电流容量加权的风电场短路电流计算方法的误差。
4.2 机组故障穿越方式 4.2.1 DFIG故障穿越方式在DFIG采用不同的故障穿越方式时,DFIG本身将表现出不同的暂态特性,从而使得多机暂态相互影响呈现不同的表现形式。当Crowbar动作时,DFIG表现出负阻抗特性,多DFIG并联对1号DFIG短路电流的作用表现为式中分母阻抗的增大,多PMSG并联对1号DFIG短路电流的作用表现为电流线性叠加效果;当Crowbar不动作时,DFIG表现为恒功率的受控电流源,此时多DFIG并联增大了分母阻抗,多PMSG并联对1号DFIG工频短路电流的作用则呈现非线性的情况。
4.2.2 PMSG故障穿越策略并联PMSG在故障期间采用无功优先的故障穿越策略。因此,PMSG机组数越多,单机PMSG输出无功电流越大,PMSG机群提供的无功功率越多,短路点电压越高。由于DFIG故障穿越方式不同,PMSG对1号DFIG短路电流的影响程度仍不同。
利用式分析isf_D1(m1, m2)对igf_Pfu的灵敏度有
| $ \frac{{\partial \mathit{\boldsymbol{i}}_{{\rm{sf\_D1}}}^{\left( {{\rm{m1,m2}}} \right)}}}{{\partial \mathit{\boldsymbol{i}}_{{\rm{gf\_P}}}^{{\rm{fu}}}}} = \left\{ \begin{array}{l} - \frac{{{m_2}{Z_{\rm{G}}}}}{{\frac{{{Z_{\rm{D}}}{Z_{\rm{G}}}}}{{{Z_{\rm{t}}}}} + {m_1}{Z_{\rm{G}}} + {Z_{\rm{D}}}}},{\rm{Crowbar}}\;动作,\\ \frac{{m_2^2{Z_{\rm{G}}}\mathit{\boldsymbol{i}}_{{\rm{gf\_P}}}^{{\rm{fu}}}}}{{2{m_1}{\mathit{\boldsymbol{u}}_{{\rm{m2}}}}}} - \frac{{{m_2}}}{{2{m_1}}},{\rm{Crowbar}}\;不动作。\end{array} \right. $ | (16) |
在网络参数和机组数量确定的情况下,当Crowbar动作时PMSG对1号DFIG工频短路电流的影响一定,1号DFIG工频短路电流随PMSG短路电流增大而增大。当Crowbar不动作时,其结果与PMSG短路电流本身大小有关:PMSG无功增益越大,短路电流越大,对1号DFIG工频短路电流的影响越小,即1号DFIG工频短路电流随PMSG短路电流的增大而减小。
4.3 故障严重程度故障严重程度是影响DFIG工频短路电流大小的重要因素之一。对式(13),求isf_D1(m1, m2)对Zf的灵敏度有
| $ \frac{{\partial \mathit{\boldsymbol{i}}_{{\rm{sf\_D1}}}^{\left( {{\rm{m1,m2}}} \right)}}}{{\partial {Z_{\rm{f}}}}} = \left\{ {\begin{array}{*{20}{c}} { - \frac{{\left( {{m_2}{Z_{\rm{G}}}\mathit{\boldsymbol{i}}_{{\rm{gf\_P}}}^{{\rm{fu}}} + {\mathit{\boldsymbol{e}}_{\rm{g}}}} \right){Z_{\rm{D}}}{Z_{\rm{G}}}}}{{{{\left( {{Z_{\rm{D}}}{Z_{\rm{G}}} + {m_1}{Z_{\rm{G}}}{Z_{\rm{f}}} + {Z_{\rm{D}}}{Z_{\rm{f}}}} \right)}^2}}},{\rm{Crowbar}}\;动作,}\\ { - \frac{{{{\mathit{\boldsymbol{\tilde S}}}^ * }{Z_{\rm{G}}}}}{{{m_1}Z_{\rm{f}}^2{\mathit{\boldsymbol{u}}_{{\rm{m2}}}}}},{\rm{Crowbar}}\;不动作。} \end{array}} \right. $ | (17) |
由式(17)可知,Crowbar动作时,1号DFIG工频短路电流随过渡电阻Zf减小而减小,斜率随Zf减小而增大;Crowbar不动作时,1号DFIG工频短路电流随Zf减小而增大,斜率随Zf减小增大。
5 算例分析为验证混合风电场多机并联运行下DFIG短路电流的特征,利用Matlab/Simulink对混合风电场模型进行暂态仿真,结构如图 4所示。仿真系统主要参数见附录。风电场含2条馈线,分别接入3台PMSG和3台DFIG,各机组经对应升压变接入,机组间以500 m等间距分布。风电场馈线电压10 kV,通过升压变及30 km联络线接入110 kV等级的300 MVA系统。同类型机组参数相同,DFIG与PMSG额定功率、定子额定电压等参数相同,风速15 m/s。短路点设置在110 kV母线处。
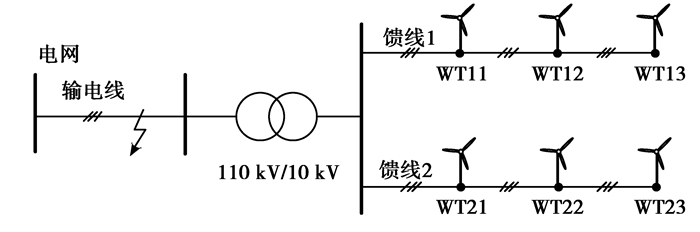
|
图 4 仿真系统结构图 Figure 4 Structure diagram of simulation system |
以WT11点接入的DFIG为1号机组,故障时间t=0.5 s。设PMSG无功增益为1.5,改变接入的机组数量,对比在Crowbar动作(过渡电阻20 Ω)和不动作(过渡电阻80 Ω)2种情况下,5台DFIG、1台DFIG和4台PMSG、1台DFIG单独接入3种情况,1号DFIG的短路电流,如图 5所示。Crowbar动作时,5台DFIG、1台DFIG和4台PMSG。1台DFIG单独接入3种情况,1号DFIG短路电流工频分量分别为0.084 0 p.u.,0.116 2 p.u.,0.105 8 p.u.;Crowbar不动作时,5台DFIG、1台DFIG和4台PMSG、1台DFIG单独接入3种情况,1号DFIG短路电流工频分量分别为1.264 p.u.,1.214 p.u.,1.322 p.u.。
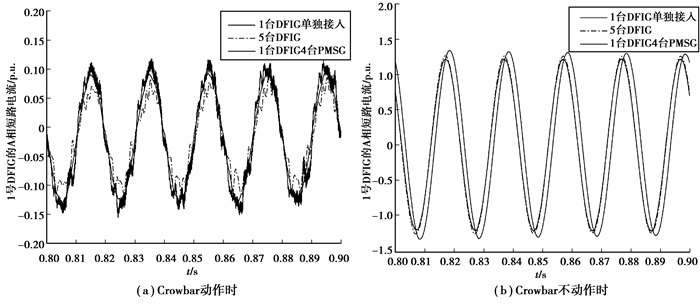
|
图 5 3种情况下1号DFIG短路电流A相波形 Figure 5 A-phase short-circuit current of No.1 DFIG in three situations |
由以上仿真结果可知,在Crowbar动作时,DFIG机组数增多使1号DFIG工频短路电流减小,PMSG机组数增多使1号DFIG工频短路电流增大;Crowbar不动作时,DFIG机组数和PMSG机组数增多均使1号DFIG工频短路电流减小:该结果符合理论分析。同时DFIG机组数增加对1号DFIG工频短路电流的影响与PMSG不同,在Crowbar动作时PMSG机组数增加使1号DFIG工频短路电流增大。
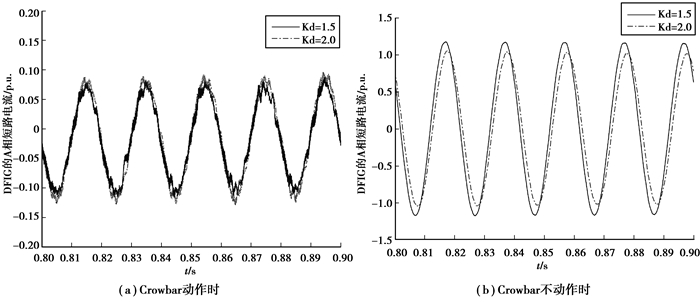
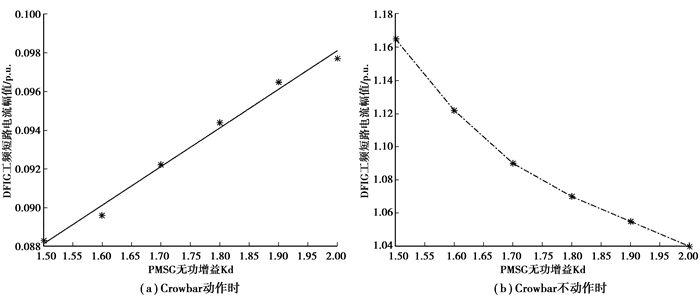
5.2 不同故障穿越策略针对DFIG的Crowbar动作的情况,设置过渡电阻Zf=20 Ω,PMSG无功增益分别为1.5和2.0时,1号DFIG短路电流A相波形如图 6(a)所示。针对DFIG的Crowbar不动作的情况,设置过渡电阻Zf=80 Ω,PMSG无功增益分别为1.5和2.0时,1号DFIG短路电流A相波形如图 6(b)所示。令PMSG无功增益从1.5逐渐增加至2.0,对1号DFIG短路电流采用离散傅里叶提取工频分量,Crowbar动作和不动作2种情况结果分别如图 7(a)和图 7(b)所示。由图 7可知,Crowbar动作时,1号DFIG工频短路电流随PMSG短路电流增大而增大,且增大的趋势近似满足线性关系;Crowbar不动作时,1号DFIG工频短路电流随PMSG短路电流增大而减小,且减小的趋势变缓:该结果符合理论分析。
|
图 6 1号DFIG短路电流A相波形 Figure 6 Wave forms of a-phase short-circuit currens of No.1 DFIG |
|
图 7 逐渐增大PMSG无功增益时1号DFIG工频短路电流幅值 Figure 7 Amplitudes of short-circuit currents of No.1 DFIG while reactive power coefficient increasing |
根据PMSG短路电流表达式,其无功电流参考值按电压跌落程度给定。在本情况中为避免引入PMSG短路电流的影响,在Crowbar动作和不动作情况下,分别给定PMSG无功电流参考值为0.7 p.u.和0.345 p.u.。针对Crowbar动作的情况,设置过渡电阻Zf从20 Ω增大至32 Ω;针对Crowbar不动作的情况,设置过渡电阻Zf从68 Ω增大至80 Ω,1号DFIG工频短路电流幅值如表 1所示。由表 1可知,Crowbar动作时,1号DFIG工频短路电流幅值随过渡电阻减小而减小,且减小趋势变陡;Crowbar不动作时,1号DFIG工频短路电流幅值随过渡电阻减小而增大,且增大趋势变陡:该变化规律与理论分析相符。
| 表 1 1号DFIG工频短路电流幅值 Table 1 Amplitudes of short-circuit currents of No.1 DFIG |
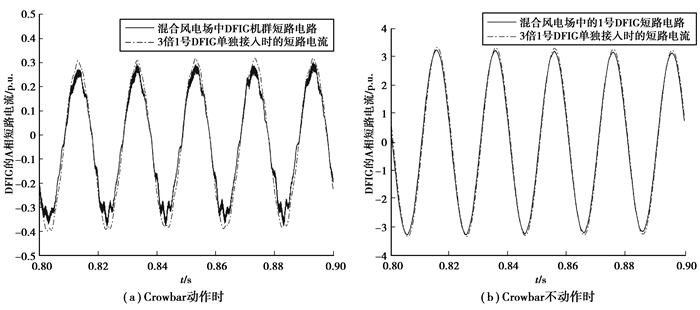
为比较多机影响下DFIG与单机DFIG接入时工频短路电流的区别,针对Crowbar动作情况和不动作2种情况,分别设置过渡电阻20 Ω和80 Ω,PMSG无功增益均为1.5,2种情况下风电场集电线DFIG机群短路电流波形与3倍单机DFIG接入时的短路电流波形对比如图 8所示。
|
图 8 混合风电场DFIG机群与3倍的1号DFIG单独接入时的短路电流对比 Figure 8 Comparison of Total Short-Circuit Current of DFIGs in hybrid wind farm and Triple Short-Circuit Current of No.1 DFIG alone |
图 8(a)中可以看到,Crowbar动作时,混合风电场中DFIG机群短路电流小于3倍的1号DFIG单独接入时的短路电流,前者工频分量为0.289 8 p.u.,后者为0.30 p.u.,利用式(15)计算的单台DFIG工频短路电流增量为0.002 9 p.u.,DFIG机群工频短路电流增量则为0.008 7 p.u.,误差为14.7%;Crowbar不动作时(见图 8(b)),混合风电场中DFIG机群短路电流工频分量为3.189 p.u.,3倍的1号DFIG单独接入时的短路电流工频分量为3.222 p.u.,利用式(15)计算的单台DFIG工频短路电流增量为0.010 2 p.u.,DFIG机群工频短路电流增量则为0.030 6 p.u.,误差为9.09%。可见在Crowbar动作和不动作两种情况下,对于DFIG机群工频短路电流相对于3倍的1号DFIG单独接入时的短路电流工频分量的增量,式(15)计算结果基本准确。
6 结论DFIG和PMSG是目前混合风电场中两种主要的机型,多机组混合运行时DFIG的短路电流特征会受到影响。针对风电场短路电流分析尚未考虑机组混合运行时相互影响的情况,通过对混合风电场中DFIG短路电流特征的研究,得出了以下主要结论:
1) DFIG短路电流在混合风电场中与单机接入时具有不同的特征,混合风电场中的DFIG同时受到并联DFIG和PMSG的影响。Crowbar动作和不动作时并联DFIG机组越多,DFIG工频短路电流越小。Crowbar动作时,并联PMSG机组越多,DFIG工频短路电流越大;Crowbar不动作时,并联PMSG机组数越多,DFIG工频短路电流越小。
2) 并联DFIG和PMSG对DFIG工频短路电流的影响与DFIG的穿越方式有关。当Crowbar动作时,并联DFIG对DFIG短路电流的作用表现为DFIG机群等效阻抗减小,并联PMSG对DFIG短路电流的作用表现为电流叠加效果;当Crowbar不动作时,并联DFIG和PMSG均为受控源,通过输出电流的叠加改变了DFIG的机端电压。
3) 并联DFIG和PMSG对DFIG工频短路电流的影响与PMSG故障穿越策略有关,且其关系也与DFIG故障穿越方式存在一定关联。DFIG的Crowbar动作时,DFIG短路电流随PMSG短路电流增大而线性增大;Crowbar不动作时,DFIG短路电流随PMSG短路电流增大而减小,斜率随PMSG短路电流增大而减小。
4) 并联DFIG和PMSG对DFIG短路电流的影响与电网故障程度有关。Crowbar动作时,DFIG工频短路电流随过渡电阻减小而减小,斜率随过渡电阻减小而增大;Crowbar不动作时,DFIG工频短路电流随过渡电阻减小而增大,斜率随过渡电阻减小而增大。
风电场整体短路电流的分析对电力系统保护和控制具有重要的意义。传统按单机短路电流容量加权方式计算混合风电场中DFIG机群的短路电流存在误差,所提出的结论对于修正容量加权计算短路电流的方法的结果、提高计算准确性具有一定的参考价值,可进一步用于风电场等值建模的研究。
附录| DFIG机组参数: | |||
| 机端电压:575 V | 额定容量:1.5 MW | 定子电阻:0.023 p.u. | 转子电阻:0.016 p.u. |
| 定子漏感:0.18 p.u. | 转子漏感:0.16 p.u. | 激磁电感:2.9 p.u. | |
| PMSG机组参数: | |||
| 机端电压:575 V | 额定容量:1.5 MW | 定子电阻:0.015 7 p.u. | 定子电感:0.325 p.u. |
| 转子磁链:1.188 421 p.u. | |||
| 机组出口升压变参数: | |||
| 额定容量:1.75 MW | 额定电压:高压侧10 kV,低压侧575 V | ||
| 额定电感:高压侧0.071 05 H 低压侧0.018×10-3 H | |||
| 馈线线路参数: | |||
| 等效电阻:0.132 Ω/mm; | 等效电感:1.136 9×10-3H/km | ||
| 输电线线路参数: | |||
| 等效电阻:0.115 3 Ω/mm; | 等效电感:1.05×10-3H/km | 线路长度:30 km | |
| [1] |
李俊峰.2014中国风电发展报告[R].北京: 中国循环经济协会可再生能源专业委员会, 2014. LI Junfeng. 2014 China wind power development report[R]. Beijing: China Recycling Economy Association renewable energy Specialized Committee, 2014. (in Chinese) |
| [2] |
姚骏, 余梦婷, 陈知前, 等. 电网对称故障下含DFIG和PMSG的混合风电场群的协同控制策略[J]. 电工技术学报, 2015, 30(15): 26-36. YAO Jun, YU Mengting, CHEN Zhiqian, et al. Coordinated control strategy for hybrid wind farms with DFIG and PMSG under symmetrical grid faults[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 26-36. (in Chinese) DOI:10.3969/j.issn.1000-6753.2015.15.003 |
| [3] |
Kong X, Zhang Z, Yin X, et al. Study of fault current characteristics of the DFIG considering dynamic response of the RSC[J]. IEEE Transactions on Energy Conversion, 2014, 29(2): 278-287. DOI:10.1109/TEC.2014.2309694 |
| [4] |
Hu S J, Wang L L, Deng Y, et al. Analysis on power output capability and its power control strategy of DFIG wind turbine under unbalanced grid voltage[J]. Applied Mechanics & Materials, 2014, 448-453: 1819-1824. DOI:10.1109/TEC.2014.2309694 |
| [5] |
毕天姝, 刘素梅, 薛安成, 等. 具有低电压穿越能力的双馈风电机组故障暂态特性分析[J]. 电力系统保护与控制, 2013, 41(2): 26-31. BI Tianshu, LIU Sumei, XUE Ancheng. Fault analysis of doubly fed induction generator wind turbines with low-voltage ride-through capability[J]. Power System Protection and Control, 2013, 41(2): 26-31. (in Chinese) |
| [6] |
郑重, 杨耕, 耿华. 电网故障下基于撬棒保护的双馈风电机组短路电流分析[J]. 电力自动化设备, 2012, 32(11): 7-15. ZHENG Zhong, YANG Geng, GENG Hua. Short circuit current analysis for DFIG-based wind generation system with Crowbar protection under grid faults[J]. Electric Power Automation Equipment, 2012, 32(11): 7-15. (in Chinese) |
| [7] |
Xiao F, Zhang Z, Yin X, et al. Fault current characteristics of the DFIG under asymmetrical fault conditions[J]. Energies, 2015, 8(10): 10971-10992. DOI:10.3390/en81010971 |
| [8] |
Sulla F, Svensson J, Samuelsson O. Short-circuit analysis of a doubly fed induction generator wind turbine with direct current chopper protection[J]. Wind Energy, 2013, 16(1): 37-49. DOI:10.1002/we.v16.1 |
| [9] |
Ouyang J, Xiong X. Research on short-circuit current of doubly fed induction generator under non-deep voltage drop[J]. Electric Power Systems Research, 2014, 107: 158-166. DOI:10.1016/j.epsr.2013.10.008 |
| [10] |
Rahimi M, Parniani M. Dynamic behavior analysis of doubly-fed induction generator wind turbines-The influence of rotor and speed controller parameters[J]. International Journal of Electrical Power & Energy Systems, 2010, 32(5): 464-477. |
| [11] |
邢鲁华, 陈青, 吴长静, 等. 含双馈风电机组的电力系统短路电流实用计算方法[J]. 电网技术, 2013, 37(4): 1121-1127. XING Luhua, CHEN Qing, WU Changjing, et al. A practical method to calculate short-circuit current in power system connected with doubly fed induction generatorsp[J]. Power System Technology, 2013, 37(4): 1121-1127. (in Chinese) |
| [12] |
尹俊, 毕天姝, 薛安成, 等. 计及低穿控制的混合型风电场短路电流特性与故障分析方法研究[J]. 电工技术学报, 2015, 30(21): 99-110. YIN Jun, BI Tianshu, XUE Ancheng, et al. Study on Short-circuit Current and Fault Analysis Method of Hybrid Wind Farm with Low Voltage Ride-through Control Strategy[J]. Transactions of China Electro Technical Society, 2015, 30(21): 99-110. (in Chinese) DOI:10.3969/j.issn.1000-6753.2015.21.012 |
| [13] |
Pannell G, Atkinson D J, Zahawi B. Analytical Study of grid-fault response of wind turbine doubly fed induction generator[J]. IEEE Transactions on Energy Conversion, 2010, 25(4): 1081-1091. DOI:10.1109/TEC.2010.2049494 |
| [14] |
Miguel A G, Comech P M, Jesus S, et al. Modeling wind farms for grid disturbance studies[J]. Renewable Energy, 2008(33): 2109-2121. |
| [15] |
张保会, 李光辉, 王进, 等. 风电接入对继电保护的影响(二)——双馈风电场电磁暂态等值建模研究[J]. 电力自动化设备, 2013, 33(2): 1-7. ZHANG Baohui, LI Guanghui, WANG Jin, et al. Impact of wind farm integration on relay protection (2):DFIG-based wind farm electromagnetic transient equivalent model[J]. Electric Power Automation Equipment, 2013, 33(2): 1-7. (in Chinese) DOI:10.3969/j.issn.1006-6047.2013.02.001 |
| [16] |
贾俊川, 刘晋, 张一工. 电网电压故障时双馈异步发电机定子磁链的动态特性研究[J]. 中国电机工程学报, 2011, 31(3): 90-96. JIA Junchuang, LIU Jin, ZHANG Yigong. Dynamic characteristics of stator flux of doubly-fed induction generator during grid voltage fault[J]. Proceedings of the CSEE, 2011, 31(3): 90-96. (in Chinese) |
| [17] |
栗然, 高起山, 刘伟. 直驱永磁同步风电机组的三相短路故障特性[J]. 电网技术, 2011, 35(10): 153-158. LI Ran, GAO Qishan, LIU Wei. Characteristics of direct-driven permanent magnet synchronous wind power generator under symmetrical three-phase short-circuit fault[J]. Power System Technology, 2011, 35(10): 153-158. (in Chinese) |
| [18] |
孔祥平, 张哲, 尹项根, 等. 含逆变型分布式电源的电网故障电流特性与故障分析方法研究[J]. 中国电机工程学报, 2013, 33(34): 65-74. KONG Xiangping, ZHANG Zhe, YIN Xianggen, et al. Study on fault current characteristics and fault analysis method of power grid with inverter interfaced distributed generation[J]. Proceedings of the CSEE, 2013, 33(34): 65-74. (in Chinese) |
 2018, Vol. 41
2018, Vol. 41


