随着通信技术的不断发展,互联网用户的数量在不断增长,越来越多的服务要求对延迟,丢包率和数据速率提出更高挑战,使传统网络架构暴露出越来越多的问题。在这种情况下,SDN网络应运而生。SDN从数据平面解耦出控制平面。控制平面由控制器组成,负责管理整个网络;而数据平面由简化的交换机组成,交换机负责数据包的转发,该架构使得网络易于管理和升级。
对于大型网络,单个控制器的管理难以满足所有交换机的需求,需要用多个控制器来分担整个系统通信压力。但是,多个控制器的位置如何部署会影响整个网络时延以及负载均衡度。因此,合理地部署多个控制器变成SDN网络研究中的一个重要问题。
许多学者在研究SDN控制器部署问题,Heller B于2012年在文献[1]中首次提出该问题并提出了2个优化指标:平均时延和最大时延。Sallahi等[2]提出了受部署代价影响的控制器部署算法,但没有涉及数学证明和具体实现。
文献[3]对K-means算法进行了改进,然后用来解决控制器部署问题,该算法最初仅选择一个点作为聚类中心,之后逐渐增加分区的数量,可有效避免k-means结果随机的缺点,但其只考虑平均控制时延,并未考虑负载均衡和跨域通信问题。Tracy等[4]提出了改进的原始对偶、贪婪和分区算法来解决问题,同样未考虑负载均衡和跨域通信问题。文献[5]将控制器部署问题与粒子群思想结合,考虑平均控制时延和负载均衡,但没有解决跨域通信问题,且结果比较随机。Xiao等[6]将控制器部署问题与谱聚类思想相结合,虽然同时考虑了时延和负载均衡,未顾及跨域通信的问题。
文献[7]提出了一种改进的模拟退火算法解决控制器部署问题,该文献同时考虑了时延、负载均衡和跨域通信,但该算法复杂度比较高,且结果比较随机。
以上列举出的文献所提出的算法大部分只考虑了平均控制时延或最大时延,虽然有一些文献兼顾了时延和负载均衡2个指标,但很少有文献同时兼顾时延、负载均衡和跨域通信3个指标,这也是需要解决的问题。
研究提出基于蝙蝠算法的多控制器部署方法。该方法通过在迭代时不断优化平均控制时延达到最小化;通过限制控制器负载利用率达到负载均衡;并通过标签传递算法去除孤立节点以保证域内通信。
主要贡献如下
1) 定义控制器负载利用率,并通过优化该指标达到控制器间的负载均衡。
2) 定义了孤立节点,该指标确保了无跨域通信的交换机出现。
3) 提出了基于蝙蝠算法的控制器部署方法,优化了平均控制时延和控制器负载差异度。
4) 提出标签传递算法去除孤立节点。
1 控制器部署模型在SDN网络多控制器部署问题中,时延、负载均衡和跨域通信是3个重要指标。首先,在SDN网络中,存在着3种时延,分别为:交换机到交换机的时延;交换机到控制器的时延;控制器到控制器的时延。因为所有的交换机都需要与控制器频繁通信,故大多数情况下只关注交换机到控制器之间的时延。其次,在为控制器分配交换机时,应该尽量保证每个控制器控制的交换机数目大致相等,否则将会出现负载较高的控制器由于超负荷停止工作,而负载较低的控制器只发挥出小部分的性能导致能源浪费。除此之外,希望控制器之间负载均衡的同时,每个控制器的实际负载不超过其最大负载。因此,提出控制器负载利用率的概念,通过限制最大和最小的控制器负载利用率使得每个控制器既不超负荷工作,又可以使得交换机的资源得到有效利用。最后,在分配完成的网络拓扑中,不应该出现跨域通信的交换机。因此多控制器的部署问题等效于:给定一个SDN网络拓扑,如果需要部署K个控制器,这K个控制器应部署在哪些位置,以及每个交换机应分配到哪个控制器,才能保证网络的时延最小、控制器之间的负载最均衡以及没有跨域通信的交换机。
同时考虑到SDN控制器类似于服务器,需要与交换机进行通信,因此控制器的部署位置即为其直接相连交换机的位置。与控制器直接相连的交换机与控制器之间的延迟理想化为0,且不需要为控制器和直连的交换机之间铺设单独的物理链路。
将SDN网络拓扑建模为一个无向图:G=(V, E),将网络中的交换机抽象为无向图中的节点,交换机和交换机之间的物理链路抽象为无向图中的边。其中V表示网络拓扑中所有节点的集合;E表示网络拓扑中所有边的集合。假设整个网络需要被划分成K个类,每个类中的交换机只由唯一的一个控制器控制,网络中交换机的个数为N,控制器的个数为K。因此,
交换机的集合表示为
| $ V = \left\{ {{v^1},{v^2}, \cdots ,{v^N}} \right\},s.t.{v^i} \in {R^n},i = 1,2, \cdots ,N, $ | (1) |
控制器的集合表示为
| $ C = \left\{ {{c^1},{c^2}, \cdots ,{c^K}} \right\},s.t.{c^i} \in {R^n},i = 1,2, \cdots ,K, $ | (2) |
交换机之间的延迟表示为
| $ d\left( {m,n} \right),{\rm{s}}.{\rm{t}}.m,n \in V, $ | (3) |
上式中(m, n)表示交换机m(m∈V)到交换机n(n∈V)的最短路径。
控制器j控制的交换机集合为SVj,控制器j控制的交换机个数为Nj,交换机i属于的控制器表示为C(vi),则
| $ S{V_j} = \left\{ {{v^i} \in V:C\left( {{v^i}} \right) = {c^j}} \right\}, $ | (4) |
每个交换机所属的控制器(也叫做每个交换机的标签)构成集合Tag,则
| $ {\rm{Tag}} = \left\{ {C\left( {{v^1}} \right),C\left( {{v^2}} \right), \cdots ,C\left( {{v^N}} \right)} \right\},{\rm{s}}.{\rm{t}}.{v^i} \in {R^n},i = 1,2, \cdots ,N。$ | (5) |
根据OpenFlow协议,分别定义平均控制时延、控制器负载差异度、控制器负载利用率和跨域通信4个指标。
定义1:平均控制时延
在SDN网络中,控制器负责处理交换机上传的新流。在OpenFlow协议中,当一条新流到达交换机时,交换机会从本身存储的流表项中查找是否有与新流匹配的流表项,若存在匹配的流表项,则按照对应规则进行操作;若不存在匹配的流表项,则该交换机将向控制器发送packet_in消息,需要控制器对新流做出响应。当控制器处理对新流处理完成后,向该交换机发送packet_out消息告知该交换机如何处理该新流,从而完成该新流的转发。从上述OpenFlow的工作机制中可以看出,交换机与控制器之间会进行频繁的通信,因此在该模型中,主要考虑交换机到控制器的查询时延,即packet_in消息与packet_out消息的时延。在仿真中只计算单程的时延。
定义控制器与交换机的平均控制时延为所有交换机到为其分配的控制器时延的平均值。公式表示如下
| $ L = \frac{1}{N}\sum\limits_{{v^i} \in V} {d\left( {{v^i},C\left( {{v^i}} \right)} \right)} ,{\rm{s}}.{\rm{t}}.{v^i} \in {R^n},i = 1,2, \cdots ,N, $ | (6) |
其中L表示平均控制时延。
定义2:控制器负载差异度
定义控制器负载差异度为每个控制器控制的交换机数量的方差,公式表示如下
| $ T = {\sigma ^2} = \sum\limits_j^K {\frac{{{{\left( {{N_j} - {N_{{\rm{average}}}}} \right)}^2}}}{K}} , $ | (7) |
| $ {N_{{\rm{average}}}} = \frac{N}{K}。$ | (8) |
其中T表示负载差异度。通过式(7)和式(8)可以看出,控制器负载差异度表现了各控制器控制交换机数量的差异,能够很好体现出控制器间负载均衡的思想。
定义3:控制器负载利用率
该指标约束了控制器的负载利用率。假设所有控制器的性能均相同,即每个控制器的最大额定负载相同。定义Cmax为控制器的最大额定负载,即每个控制器可以控制交换机的最大数目。则第j个控制器的实际负载利用率为
| $ {\rm{ratio}}_{{\rm{real}}}^j = \frac{{{N_j}}}{{{C_{\max }}}},j = 1,2, \cdots ,K, $ | (9) |
其中ratiorealj为第j个控制器的实际负载利用率。
则实际负载利用率需要满足
| $ {\rm{rati}}{{\rm{o}}_{\min }} \le {\rm{ratio}}_{{\rm{real}}}^j \le {\rm{rati}}{{\rm{o}}_{\max }},\forall j \in K, $ | (10) |
其中ratiomin和ratiomax分别为控制器的最大和最小负载利用率。
定义4:孤立节点数
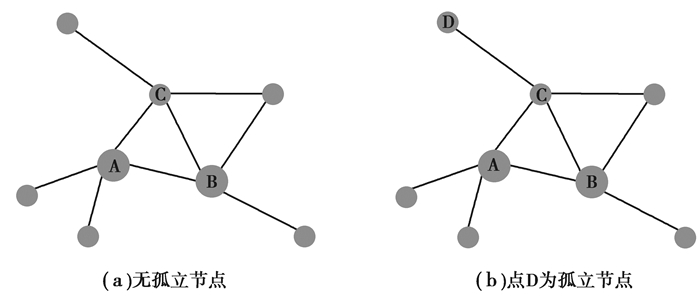
该指标定义了提及的跨域通信问题,可以抽象为图的连通性的问题。如图 1(a)所示,该网络被分成2个类,A类和B类,中心点分别为A点和B点,即控制器的部署位置。从图中可以看出,A类共有5台交换机,B类共有3台交换机。根据定义2控制器负载差异度的需要,可以将A类中的一个点分配给B类。
|
图 1 孤立节点示意图 Figure 1 The isolated nodes diagram |
出于平均控制时延最小化的考虑,将C点分配给B类,分类后的结果如图 1(b)所示。而此时由于将C点分配给B类,导致了D点与中心点A的不连通,A区域被隔离开来,使初始时D点与中心点A之间的域内通信改变为跨域通信。跨域通信有可能出现可靠性、稳定性、安全性等一系列的问题。
用孤立节点数来判断网络中是否有跨域通信的情况存在。如果网络中无跨域通信的交换机存在,则必须满足孤立节点数为0,即
| $ IN = 0, $ | (11) |
其中IN为孤立节点数。
基于以上的3个定义,多控制器部署问题可以被建模为一个多目标优化问题[8]。目标函数及约束可表示为
| $ \min \mathit{\boldsymbol{F}}\left( {C\left( {{v^i}} \right),S{V_j}} \right) = {\left( {L,T} \right)^{\rm{T}}}, $ | (12) |
| $ {\rm{s}}{\rm{.t}}{\rm{.rati}}{{\rm{o}}_{\min }} \le {\rm{ratio}}_{{\rm{real}}}^j \le {\rm{rati}}{{\rm{o}}_{\max }},\forall j \in K, $ | (13) |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}IN = 0。$ | (14) |
以上即为多控制部署问题的数学模型,该多目标优化问题是一个NP-hard问题,无法在多项式时间内求出最优解。因此,提出一种基于蝙蝠算法的多控制器部署方法,来近似求得该问题的最优解。
2 基于蝙蝠算法的多控制器部署方法研究提出了基于蝙蝠算法的多控制器部署方法(BACP, a bat inspired controller placement algorithm in software defined network)。蝙蝠算法[9]是一种启发式算法,它仿照自然界中蝙蝠的回声定位,利用脉冲响度和脉冲发射频率的适时改变来实现算法的全局搜索和局部搜索自动切换,从而平衡全局搜索和局部搜索对算法寻最优解的影响。
2.1 蝙蝠位置定义及初始化每只蝙蝠的位置代表一种分类策略,每个交换机所属的控制器集合Tag可以看做一只蝙蝠的位置,即在网络G=(V, E)中,所有交换机集合为V={v1, v2, …, vN},交换机的个数为N,一只蝙蝠的位置构成集合Tag={C(v1), C(v2), …, C(vN)},对于网络中的任意2个交换机i, j,若C(vi)=C(vj),则表示交换机i, j属于同一个控制器。可以看出,该问题的解空间是一个N维的向量。为了保证解空间的随机性,初始时随机选取每只蝙蝠的位置。
2.2 蝙蝠速度定义及初始化在多控制器部署问题中,每只蝙蝠的位置每一维解(每只蝙蝠共有N维解),即每个交换机所属的控制器, 只有更新和不更新2种方式,因此定义第i只蝙蝠的速度:Vi={v1, v2, …, vN}, (vj∈[0, 1])。若某速度分量为1,则该位置元素进行更新;若某速度分量为0,则该位置元素不进行更新。初始时,假设所有速度分量均为1,即每个位置元素都有可能进行更新。
2.3 蝙蝠速度及位置更新规则假设每只蝙蝠可以记住自己的历史最优位置,且每只蝙蝠可以知道所有蝙蝠的全局最优位置。结合蝙蝠算法的基本原理和多控制器部署问题,定义蝙蝠速度及位置更新规则如下
| $ V_i^{t + 1} = \mathit{\boldsymbol{F}}\left( {V_i^t + \left( {{\rm{Tag}}_i^t \oplus {\rm{Ta}}{{\rm{g}}_{{\rm{best}}}}} \right) \times {f_i}} \right), $ | (15) |
| $ {\rm{Tag}}_i^{t + 1} = {\rm{Tag}}_i^t \otimes V_i^{t + 1}, $ | (16) |
| $ {f_i} = {f_{\min }} + \left( {{f_{\max }} - {f_{\min }}} \right) \times \beta 。$ | (17) |
其中Vit和Vit+1分别表示蝙蝠个体i在t时刻和t+1时刻的速度;Tagit和Tagit+1分别表示蝙蝠个体i在t时刻和t+1时刻的位置;Tagbest表示所有蝙蝠个体的全局最优位置。fi表示蝙蝠个体i的搜索频率;fmin和fmax分别表示蝙蝠发射脉冲频率的最小和最大值;β是0~1之间的随机数。
2.3.1 蝙蝠速度更新规则:式(15)、(17)表示蝙蝠的速度更新。⊕为异或操作。
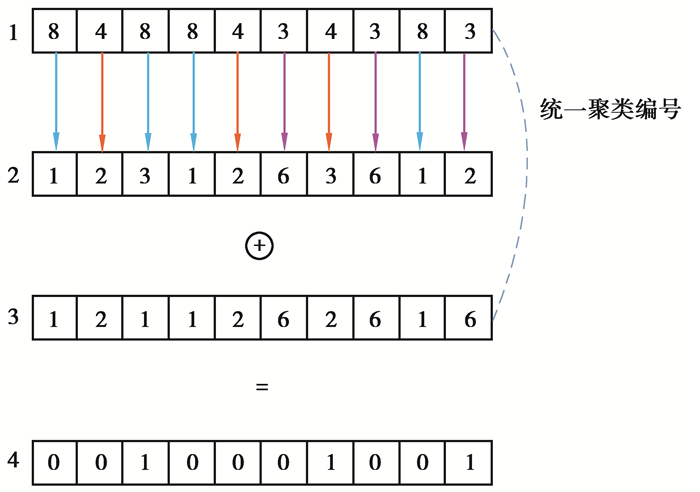
如图 2所示,由于初始化时,每个蝙蝠的位置都是随机的,因此不同蝙蝠个体之间无法直接进行异或操作,首先要将不同蝙蝠个体之间的聚类编号统一,然后蝙蝠个体1和蝙蝠个体2将进行异或操作。蝙蝠个体1中的聚类编号共有3种,分别为8, 3, 4。以编号8为例,蝙蝠个体1中共有4个位置编号为8,找到蝙蝠个体2中相对应的位置,图中用蓝色箭头标出。蝙蝠个体2中对应位置的聚类编号分别为1, 3, 1, 1。因为编号1居多,因此将蝙蝠个体1中编号为8的位置全部改为1;若以此类推。经过统一聚类编号的操作后,蝙蝠个体1的聚类编号变为个体3。此时再将蝙蝠个体2和蝙蝠个体3做异或操作。异或操作的规则为:聚类编号相同为0,聚类编号不同为1。个体4为蝙蝠个体2和3做异或操作之后的结果。
|
图 2 统一聚类编号和异或操作 Figure 2 The operation of uniform clustering number and xor |
下面给出函数Y=F(x)的定义
| $ \left\{ \begin{array}{l} Y = 0,{\rm{rand}}\left( {0,1} \right) \ge f\left( x \right)\\ Y = 1,{\rm{rand}}\left( {0,1} \right) < f\left( x \right), \end{array} \right. $ | (18) |
| $ f\left( x \right) = \frac{1}{{1 + {e^{ - x}}}}。$ | (19) |
其中rand(0, 1)是0到1之间的随机数,从式(18)和式(19)可以看出,当随机数rand(0, 1)≥f(x)时,该维度的速度为1,该维度的位置需要进行更新;当随机数rand(0, 1)<f(x),该维度的速度为0,该维度的位置不需要进行更新。
2.3.2 蝙蝠位置更新规则:式(16)表示蝙蝠位置的更新。将⊗定义为位置更新操作,位置更新操作的具体规则如下所示
| $ \left\{ \begin{array}{l} {\rm{Tag}}_i^{t + 1} = {\rm{Tag}}_i^t,v_i^{t + 1} = 0,\\ {\rm{Tag}}_i^{t + 1} = {\rm{Position}}\left( {{\rm{Tag}}_i^t} \right),v_i^{t + 1} = 1, \end{array} \right. $ | (20) |
其中vit+1为某一蝙蝠个体在t+1时刻的第i维的速度分量;Tagit和Tagit+1分别表示t时刻和t+1时刻该蝙蝠个体在第i维的位置分量。
式(20)表示,若某一维的速度分量为0,则该维的位置分量不进行更新;若某一维的速度分量为1,则该维的位置分量通过Position操作进行更新。Position操作如下:
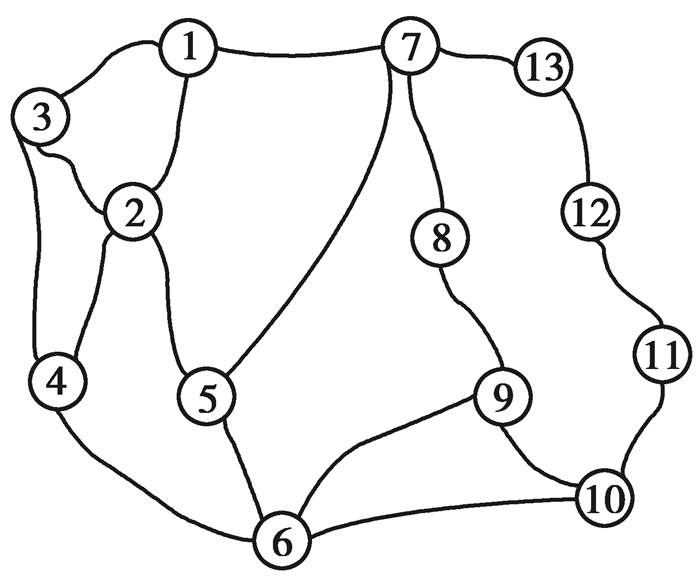
如图 3所示,以节点1为例,假设此时节点1的位置分量为1,即节点1需要进行Position操作。此时节点1的邻居节点为2, 3, 7。节点2, 3的中心点为4,节点7的中心点为12。因此节点1分配给中心点4的概率为2/3,分配给中心点12的概率为1/3。
|
图 3 Position操作示意图 Figure 3 The position operation |
Algorithm 1:BACP算法
1) 输入:初始化算法所需的参数,包括蝙蝠个体数量,衰减系数,最大迭代次数,最大额定负载,最大最小负载利用率等;
2) 根据方法,随机初始化蝙蝠种群位置Tagi0={C(v1), C(v2), …, C(vN)},初始化蝙蝠种群的速度Vi0={v1, v2, …, vN}, (vj=1),初始化蝙蝠种群的脉冲频度ri0和脉冲响度Ai0。初始时每只蝙蝠的最优位置Tagibest即为其初始位置Tagi0。
3) 根据式(6)和式(10)计算每只蝙蝠个体的平均控制时延以及控制器实际负载利用率。在这里,只以最大控制器负载利用率最小化为评价指标,从中选出最优个体(即控制器负载差异度最小的个体),作为当前的全局最优解。
4) 根据提出的更新规则,更新每只蝙蝠个体的位置Tagit。根据平均时延最小化的原则,重新选择每个类的中心点,并更新Tagit。
5) 由于每只蝙蝠个体的位置初始化时是随机的,因此极有可能出现孤立节点,在此利用提到的标签传递算法对Tagit去除孤立节点。有关标签传递算法的内容在下节中详细介绍。
6) 根据更新后的Tagit,计算平均控制时延和最大控制器负载利用率。若2项指标中有一个减小,则更新蝙蝠个体i的最优解Tagibest;否则不进行更新。
7) 对于每只蝙蝠个体,计算每只蝙蝠个体的脉冲频度rit,并产生0~1之间的随机数rand1,若rand1>rit,则在该个体最优解Tagibest附近产生扰动。扰动方式如下
首先计算所有蝙蝠个体的平均脉冲响度At。对于每只蝙蝠个体最优解Tagibest的每一个位置分量,若
8) 对于每只蝙蝠个体,计算每只蝙蝠个体的脉冲响度Ait, 并产生0~1之间的随机数rand2。若rand2<Ait且Tagibest_temp的平均控制时延和控制器负载差异度均比Tagibest小,则Tagibest=Tagibest_temp。
9) 根据更新过后的每只蝙蝠个体最优解,以平均控制时延和最大控制器负载利用率最小化为标准,且需要满足式(11)的控制器负载利用率的约束,更新全局最优解。
10) 分别按照以下2个公式更新rit和Ait
| $ r_i^{t + 1} = r_i^0 \times \left[ {1 - \exp \left( { - \gamma t} \right)} \right], $ | (21) |
| $ A_i^{t + 1} = \alpha \times A_i^t。$ | (22) |
其中γ通常取1;α为衰减系数,通常取值为0.99或0.98。
11) 若达到最大迭代次数或全局最优解连续几次不再改变,则终止并输出全局最优解;否则,转至第4步;
3 标签传递算法通过多控制器部属方法能实现最小化延迟和负载均衡,但无法保证连通性。因此,引入标签传递算法保证节点与中心点之间的连通性,保障域内通信。标签传递算法首先利用广度优先算法的思想找到网络中的孤立节点,并按照规则重新分配这些孤立节点。
Algorithm 2:标签传递算法
1) 输入:网络拓扑G=(V, E),中心点集合C、所有点标签集合Tag。
2) 输出:中心点集合C、所有点标签集合Tag。
3) 第一步:选取其中的一个类,该类中心点的标签为黑色标签,该类其余节点的标签为白色。
4) 第二步:基于广度优先算法的思想,将与黑色标签节点相邻的白色节点的标签改变为黑色,以此类推,直到所有的黑色标签节点不再有相邻的白色标签节点。
5) 第三步:遍历所有类,对每个类重复第一步和第二步。此时标签为白色的节点即为孤立节点,将所有标签为白色的节点放置于集合isolated_nodes中。
6) 第四步:遍历isolated_nodes中所有元素,即所有孤立节点。
若孤立节点的相邻节点不是孤立节点:则将该孤立节点的中心点改为其相邻节点的中心点,若该孤立节点有多个相邻节点,则说明该孤立节点可以属于多个类,此时将该孤立节点的中心点更改为距离该孤立节点最近的中心点;
若孤立节点的相邻节点是孤立节点:则暂时不分配该孤立节点。
7) 第五步:重复第1, 2, 3步。
若isolation_nodes=∅,则返回C和Tag。
若isolation_nodes≠∅,则回到第4步。
4 实验与分析 4.1 仿真参数及指标仿真使用拓扑为AL2S(america internet2 network advanced layer2 services topology)[8]。该网络拓扑共有39个节点,49条边,是目前较为标准的实际SDN网络。许多关于SDN控制器部署的文献都使用该拓扑进行方法验证[1, 11]。
仿真中使用到的参数如表 1所示
| 表 1 仿真参数表 Table 1 Simulation parameters |
假设信号在物理链路中的传播速度是光速的
| $ {\rm{latency}} = \frac{{{\rm{distance}}\left( m \right)}}{{2 \times {{10}^8}\left( {{\rm{m/s}}} \right)}}, $ | (23) |
仿真指标使用前面的平均控制时延、控制器负载差异度和孤立节点数。
4.2 实验结果与分析将BACP算法与经典K-means算法和文献[5]中提出的NCPSO算法进行比较,文献[5]基于粒子群算法提出了NCPSO算法解决SDN网络中的多控制器部署问题。
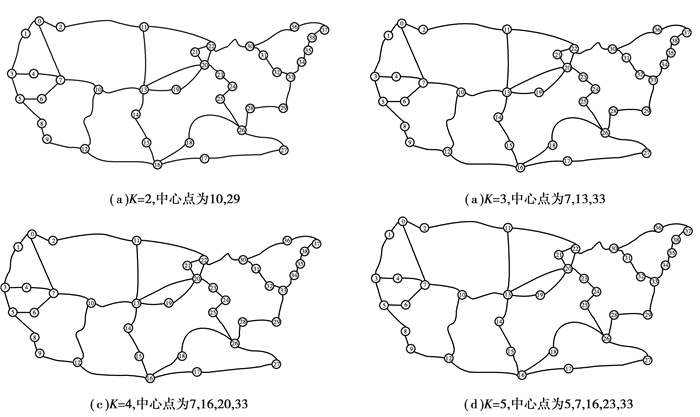
4.2.1 AL2S拓扑分类结果将AL2S拓扑中的39个节点分别进行标号,0~38。图 4是AL2S拓扑分成2, 3, 4, 5类的结果图,不同颜色表示不同的分区。划分结果较为均匀,表明提出的BACP算法具有保证负载均衡和最小时延的有效性。
|
图 4 AL2S拓扑分类结果 Figure 4 The clustering results of AL2S topology |
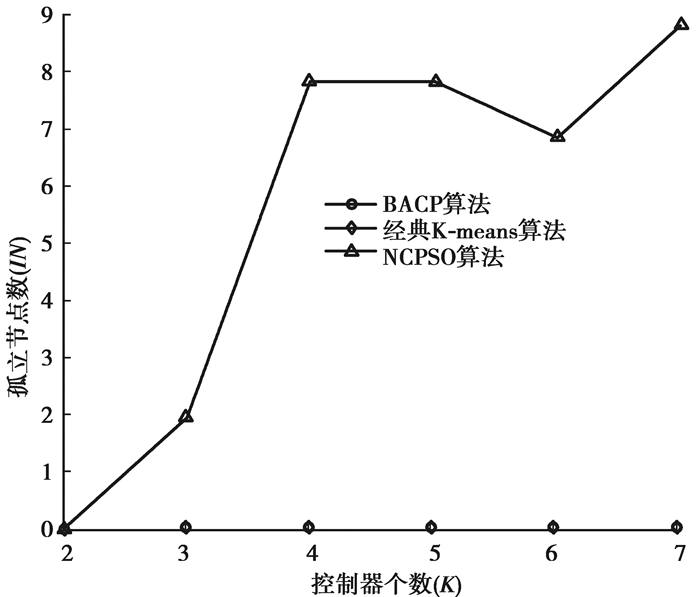
图 5是3种算法随着分类数不断增加的孤立节点数。从图 5中可以看出,经典K-means算法和BACP算法没有出现孤立节点。由于K-means算法只根据距离来分配节点,因此不会出现孤立节点。BACP算法通过标签传递算法去除了孤立节点。而NCPSO算法由于存在大量随机因素,因此会出现孤立节点。
|
图 5 孤立节点数变化 Figure 5 The change trend of isolated nodes numbers |
图 6是3种算法随着控制器个数不断增加的平均控制时延。其中ratiomin=50%。从图 6中可以看出,随着控制器个数的不断增加,平均控制时延逐渐减小,这与平均控制时延的定义相符。NCPSO算法的平均控制时延基本和经典K-means相当,略高于经典的K-means。总的来说,BACP算法通过多次迭代,平均控制时延基本比NCPSO和经典K-means算法的平均控制时延略小。只有在K=5和7时,BACP的平均控制时延略高于经典K-means的时延,但与NCPSO相比,BACP的时延一直都较小。

|
图 6 平均控制时延变化 Figure 6 Comparison of the AL2S topology partition in terms of arerage latency |
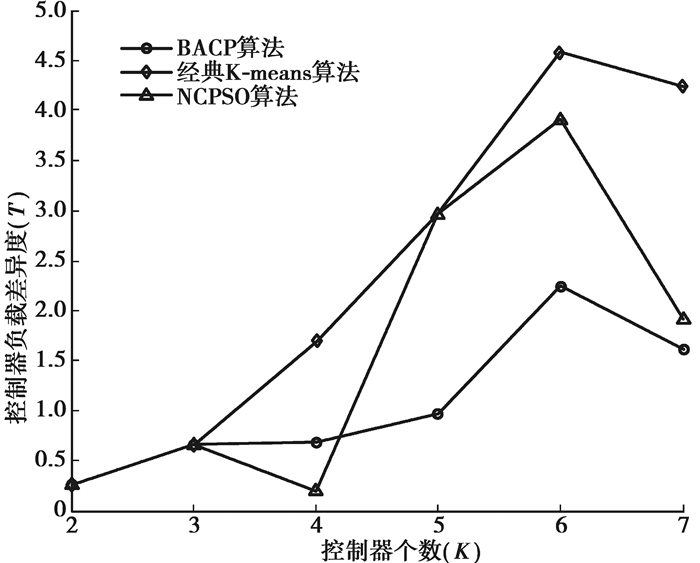
图 7是3种随着分类数不断增加的控制器负载差异度图。从图中可以看出,BACP算法在该性能的表现大体上优于NCPSO和经典K-means算法。K=5时,优于NCPSO算法67%,优于经典K-means算法67%;K=6时,优于NCPSO算法42%,优于经典K-means算法51%;K=7时,优于NCPSO算法16%,优于经典K-means算法62%;只有在K=4时表现略差,低于NCPSO算法73%。
|
图 7 控制器负载差异度变化 Figure 7 Comparison of the AL2S topolagy partition in terms of controller load balamce index |
综合图 6和图 7,尽管在允许的范围内,BACP算法在平均控制时延上偶尔表现略差,但是在控制器负载差异度上表现优异。BACP算法可以在牺牲较小平均控制时延的情况下,大幅度降低控制器负载差异度和孤立节点数,证明了BACP算法的有效性。
5 结论提出了基于蝙蝠算法的多控制器部署方法。该方法利用蝙蝠算法的思想,通过在迭代时不断优化平均控制时延达到平均控制时延最小化;通过限制控制器负载利用率保证更控制器间负载均衡;同时,利用标签传递算法去除孤立节点保证域内通信。仿真结果表明该方法在3个指标上均有良好的性能,可获得合理的SDN多控制器部署方案。
| [1] |
Heller B, Sherwood R, Mckeown N. The controller placement problem[J]. ACM Sigcomm Computer Communication Review, 2012, 42(4): 473-478. DOI:10.1145/2377677 |
| [2] |
Sallahi A, St-hilaire M. Optimal model for the controller placement problem in software defined network[J]. IEEE Communications Letters, 2015, 19(1): 30-33. DOI:10.1109/LCOMM.2014.2371014 |
| [3] |
Wang G, Zhao Y, Huang J, et al. A k-means-based network partition algorithm for controller placement in software defined network[C]//2016 IEEE International Conference on Communications (ICC). Kuala, Malaysia: IEEE, 2016: 1-6.
|
| [4] |
Cheng T Y, Wang M, Jia X. QoS-guaranteed controller placement in SDN[C]//2015 IEEE Global Communications Conference (GLOBECOM). London UK: IEEE 2015: 1-6.
|
| [5] |
Liu S, Wang H, Yi S, et al. NCPSO: a solution of the controller placement problem in software defined networks[C]//International Conference on Algorithms and Architectures for Parallel Processing. China: Springer International Publishing, 2015: 213-225.
|
| [6] |
Xiao P, Qu W, Qi H, et al. The SDN controller placement problem for WAN[C]//Communications in China (ICCC), 2014 IEEE/CIC International Conference, 2014. Qingdao, China: IEEE, 220-224.
|
| [7] |
覃匡宇, 黄传河, 王才华, 等. SDN网络中受时延和容量限制的多控制器均衡部署[J]. 通信学报, 2016, 37(11): 90-103. QIN Kuangyu, HUANG Chuanhe, WANG Caihua, et al. SDN networks are subject to delay and capacity constrained multi controller deployment[J]. Journal of Communications, 2016, 37(11): 90-103. DOI:10.11959/j.issn.1000-436x.2016219 |
| [8] |
Hillermeier C. Nonlinear multi-objective optimization[M]. Basel: Birkhaüser Verlag, 2001.
|
| [9] |
Yang X S. A new metaheuristic bat-inspired algorithm[J]. Computer Knowledge & Technology, 2010(284): 65-74. |
| [10] |
AL2S Topology[EB/OL], Internet2 Network NOC https://noc.net.internet2.edu/i2network/advanced-layer-2-service/maps-documentation/al2s-topology.html.
|
| [11] |
Yao G, Bi J, Li Y, et al. On the capacitated controller placement problem in software defined network[J]. IEEE Communications Letters, 2014, 18(8): 1339-1342. DOI:10.1109/LCOMM.2014.2332341 |
 2018, Vol. 41
2018, Vol. 41


