2. 重庆邮电大学 计算机科学与技术学院, 重庆 400065
2. School of Computer Science and Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, P. R. China
行人再识别目标是在无重叠的视频监控系统中,识别不同视频中出现的行人目标是否属于同一行人。由于不同摄像机场景下行人受摄像机自身特性、光照、视角、姿势以及遮挡等因素的影响,同一行人外观存在很大的差异,使得行人再识别问题面临很大挑战。针对上述问题,国内外研究人员提出了许多行人再识别方法,主要分为2类:基于特征表示法[1-4]和基于距离度量学习法[5-9]。
基于特征表示的方法目的在于设计鲁棒且具有判别性的行人图像特征模型,提取特征应该对光照、视角变化具有鲁棒性,同时能够区分不同的行人。文献[10]将人体按照人体结构划分成不同区域,分别提取加权HSV直方图和纹理特征并对不同的特征采用不同的距离函数计算距离,最终距离按照不同的权重将不同特征的距离加权求和得到。文献[11]将行人图像在垂直方向从上到下分成6个水平带,分别提取HSV颜色直方图特征和Gabor特征,并串联在一起形成行人图像特征向量。文献[12]提出基于块集合表示的方法,将行人图像划分成重叠的小块,对每个小块提取颜色直方图特征和局部不变特征。文献[13]提出了局部直方图特征判别累积方法,根据局部直方图尺寸的不同,分析图像位置的差异性,根据映射构造加权局部直方图,形成一个特征向量。虽然基于特征表示法模型简单,但由于实际应用中行人图像在光照、视角、姿势等变化下,同一行人外观变化很大,导致很难提取到具有判别性和鲁棒性的特征,因此,该方法识别效果很差。
目前,距离度量学习已成为行人再识别中最受欢迎的方法,其主要是学习得到一个分类器或排序模型。具有代表性的距离度量学习方法有最大边界最近邻(large margin nearest neighbor,LMNN)[14-15]、信息理论度量学习(information theoretic metric learning,ITML)[16]、逻辑判别度量学习(logistic discriminant metric learning,LDML)[17]等。基于距离度量学习的行人再识别方法目的是利用已标注样本的信息,通过训练学习得到一个测度矩阵,即将样本从原始特征空间投影到另一个更具区分性的特征空间,从而使同类样本间距离尽可能小,异类样本间距离尽可能大。虽然基于度量学习的行人再识别方法具有良好的性能,但是实际情况由于缺少足够多的训练样本,导致大都基于度量学习的方法遇到小样本问题。
引用正则化线性判别分析算法(regularized linear discriminant analysis,RLDA)[18]通过给类内散度矩阵加一个小的扰动,使其非奇异,从而解决小样本问题。但是,当数据维度很高时,RLDA算法需要求解一个d×d维(d为输入样本的特征维数)的散度矩阵,计算和存储代价大,而使用PCA等降维算法对数据进行预处理时,可能会丢失一些有利于RLDA的判别信息,从而影响算法的性能。因此,使用核函数替代上述的方法,提出了基于卡方核的正则化线性判别分析行人再识别算法(kernel regularized linear discriminant analysis,KRLDA)。引入核函数的主要目的是提高分类效果,由于现实中的行人样本数据之间关系可能是线性不可分的,加核后通过相应核函数将样本映射到线性可分的高维空间,利用高维度空间样本在可分状态下的拓扑关系获得样本之间的散度矩阵,使学习到的投影矩阵将样本投影到低维空间后,样本依然保持了高维空间的可分性。此外,采用核函数的好处是不需要真实进行高维空间中样本的点乘运算,可用核函数计算值代替,因此可提高计算速度。
1 正则化线性判别分析在实际应用LDA进行行人再识时,由于样本的特征维数远远大于训练集中样本的个数,使得该方法通常遇到小样本问题,导致类内散度矩阵奇异性,最终无法求解最优投影矩阵。为了避免可能出现的小样本问题和类内散度矩阵奇异,近年来,相继提出了许多LDA改进方法,包括Friedman提出的正则化LDA(RLDA)、Chen[19]等提出的零空间LDA(NLDA)、Yu和Yang[20]提出的直接LDA(DLDA)等。使用RLDA方法通过给类内散度矩阵加入一个小的扰动使其非奇异,克服了LDA的小样本问题,并提高了识别率。
设X={xij|i=1, …, c; j=1, …, Ni}∈Rd×N为训练样本集,d为样本的维数,c是样本的类别数,Xij表示第i类样本中的第j个样本,Ni表示第i类样本的个数,且满足N=N1+N2+…+Nc。则样本的类内散度矩阵Sw以及类间散度矩阵Sb分别定义如下
| $ {\mathit{\boldsymbol{S}}_w} = \frac{1}{N}\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^{{N_i}} {\left( {x_i^j - {m_i}} \right){{\left( {x_i^j - {m_i}} \right)}^{\rm{T}}}} } , $ | (1) |
| $ {\mathit{\boldsymbol{S}}_b} = \frac{1}{N}\sum\limits_{i = 1}^c {{N_i}\left( {{m_i} - m} \right){{\left( {{m_i} - m} \right)}^{\rm{T}}}} , $ | (2) |
其中
| $ m = \frac{1}{N}\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^{{N_i}} {x_i^j} } , $ | (3) |
| $ {m_i} = \frac{1}{{{N_i}}}\sum\limits_{j = 1}^{{N_i}} {x_i^j} , $ | (4) |
m表示所有样本的均值,mi表示第i类样本的均值。
LDA的目标是要寻找一组最佳鉴别矢量w∈Rd×d′,使样本投影到d′维子空间中,欲使投影后的样本在新的子空间内有最大的类间距离和最小的类内距离,可将目标函数定义为
| $ \mathit{\boldsymbol{w}} = \mathop {\arg \max }\limits_\mathit{\boldsymbol{w}} \frac{{{\mathit{\boldsymbol{w}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_b}\mathit{\boldsymbol{w}}}}{{{\mathit{\boldsymbol{w}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_w}\mathit{\boldsymbol{w}}}}。$ | (5) |
式(5)可通过如下广义特征值问题求解
| $ {\mathit{\boldsymbol{S}}_b}\mathit{\boldsymbol{w}} = \lambda {\mathit{\boldsymbol{S}}_w}\mathit{\boldsymbol{w}}。$ | (6) |
若类内散度矩阵Sw可逆,则式(6)可写为Sw-1Sbw=λw,那么w的最优解由Sw-1Sb的前d′个最大非零广义特征值所对应的特征向量组成(d′≤c-1)。但是,使用LDA可能会遇到小样本问题,即样本的维数大于训练样本的总数,导致类内散度矩阵Sw奇异。
为了解决Sw奇异性的问题,文献[18]采用正则化方法,将一个单位阵的倍数与之相加,用2者之和代替原来的Sw,即
| $ {\mathit{\boldsymbol{S}}_w} = {\mathit{\boldsymbol{S}}_w} + \mu \mathit{\boldsymbol{I}}, $ | (7) |
其中:I为单位矩阵,μ可为任意一个较小的正实数,实验中μ设置为0.01。
2 核正则化线性判别分析核正则化线性判别分析的思想是通过一个非线性映射φ:x→φ(x)将样本从原始特征空间映射到高维特征空间H中,然后在H中构造描述数据之间邻近关系的散度矩阵,再利用正则化线性判别分析获得高维到低维空间的投影矩阵,使得数据在低维空间中仍能够保持高维空间的可分性。原始样本集X映射到高维特征空间H中可表示为φ(X)={φ(xij)|i=1, …, c; j=1, …, Ni},其中,φ(xij)∈H。假设核矩阵K=φ(X)Tφ(X),kij=φ(X)Tφ(xij)。则在高维特征空间H中类内散度矩阵Sφw和类间散度矩阵Sφb分别定义为
| $ \mathit{\boldsymbol{S}}_w^\mathit{\boldsymbol{\varphi }} = \frac{1}{N}\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^{{N_i}} {\left( {\mathit{\boldsymbol{\varphi }}\left( {x_i^j} \right) - m_i^\mathit{\boldsymbol{\varphi }}} \right){{\left( {\mathit{\boldsymbol{\varphi }}\left( {x_i^j} \right) - m_i^\mathit{\boldsymbol{\varphi }}} \right)}^{\rm{T}}}} } , $ | (8) |
| $ \mathit{\boldsymbol{S}}_b^\mathit{\boldsymbol{\varphi }} = \frac{1}{N}\sum\limits_{i = 1}^c {\left( {m_i^\mathit{\boldsymbol{\varphi }} - {m^\mathit{\boldsymbol{\varphi }}}} \right){{\left( {m_i^\mathit{\boldsymbol{\varphi }} - {m^\mathit{\boldsymbol{\varphi }}}} \right)}^{\rm{T}}}} , $ | (9) |
其中,mφi为H中第i类样本的均值,mφ为H中所有样本的均值。
在特征空间H中,核线性判别分析的目标函数可定义为
| $ \mathit{\boldsymbol{w}} = \mathop {\arg }\limits_\mathit{\boldsymbol{w}} \max \frac{{{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{S}}_b^\mathit{\boldsymbol{\varphi }}\mathit{\boldsymbol{w}}}}{{{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{S}}_w^\mathit{\boldsymbol{\varphi }}\mathit{\boldsymbol{w}}}}。$ | (10) |
根据再生核理论[21],任意w∈H都可以表示成H中训练样本的线性组合,即存在α=(α1, α2, …, αN)T∈RN,使得
| $ \mathit{\boldsymbol{w}} = \sum\limits_{i = 1}^N {{\alpha _i}\mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right)} = \mathit{\boldsymbol{\varphi }}\left( X \right)\mathit{\boldsymbol{\alpha }}, $ | (11) |
对于任意测试样本xt,将其投影到w上可以得到
| $ \begin{array}{l} {\mathit{\boldsymbol{z}}_t} = {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( {{x_t}} \right) = {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}{\left( X \right)^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( {{x_t}} \right) = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\left[ {\mathit{\boldsymbol{\varphi }}{{\left( {{x_1}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( {{x_t}} \right) \cdots \mathit{\boldsymbol{\varphi }}{{\left( {{x_N}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( {{x_t}} \right)} \right]^{\rm{T}}} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\left[ {k\left( {{x_1},{x_t}} \right),k\left( {{x_2},{x_t}} \right), \cdots ,k\left( {{x_N},{x_t}} \right)} \right]^{\rm{T}}}, \end{array} $ | (12) |
根据式(10)、式(11)和式(12)可得
| $ \mathit{\boldsymbol{\alpha }} = \mathop {\arg \max }\limits_\mathit{\boldsymbol{\alpha }} \frac{{{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{K_b}\mathit{\boldsymbol{\alpha }}}}{{{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{K_w}\mathit{\boldsymbol{\alpha }}}}, $ | (13) |
其中,核类间散度矩阵Kb和核类内散度矩阵Kw均为N×N的对称矩阵,分别为
| $ {\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{w}}} = \frac{1}{N}\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^{{N_i}} {\left( {k_i^i - {m_i}} \right){{\left( {k_i^i - {m_i}} \right)}^{\rm{T}}}} } , $ | (14) |
| $ {\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{b}}} = \frac{1}{N}\sum\limits_{i = 1}^c {{N_i}\left( {{m_i} - m} \right){{\left( {{m_i} - m} \right)}^{\rm{T}}}} , $ | (15) |
其中
| $ {m_i} = \frac{1}{{{N_i}}}\sum\limits_{j = 1}^{{N_i}} {k_i^j} , $ | (16) |
| $ m = \frac{1}{N}\sum\limits_{i = 1}^c {\sum\limits_{j = 1}^{{N_i}} {k_i^j} } 。$ | (17) |
最后,α的最优解可由Kw-1Kb的前c-1个最大特征值对应的特征向量得到。但是Kw可能是奇异的,因此利用正则化技术给Kw加一个单位阵的倍数,即Kw=Kw+μI来解决奇异性问题,μ为常数,I为单位阵。
在基于KRLDA的行人再识别算法中,核函数的选择至关重要,选择不同的核函数将会对算法的性能产生很大的影响。一般常用的核函数如线性核、RBF核、多项式核等大多都基于欧氏距离来描述样本的不同,欧式距离只考虑各个特征量的绝对距离,往往忽视各特征量的相对距离。而卡方距离能够更有效地反映出各样本特征的相对距离变化,根据每个特征量对分类结果贡献的不同,给出卡方距离下的样本向量权重[22]。基于以上优点,笔者使用卡方核函数,提出了基于卡方核的正则化判别分析行人再识别算法。为了证明提出的卡方核效果好,选用线性核与其作了对比实验,使用的核函数具体其形式分别如下
1) 线性核(linear kernel)
| $ k\left( {x,y} \right) = {\mathit{\boldsymbol{x}}^{\rm{T}}}y。$ |
2) 卡方核(chi2 kernel)
| $ k\left( {x,y} \right) = 2\frac{{{\mathit{\boldsymbol{x}}^{\rm{T}}}y}}{{x + y}}。$ |
3) 径向基卡方核(RBF-chi2 kernel)
| $ k\left( {x,y} \right) = \exp \left( { - \frac{{{{\left( {x - y} \right)}^2}}}{{\left( {x + y} \right)\sigma }}} \right)。$ |
其中,σ为RBF核函数的参数。
3 实验及结果分析为了验证算法的有效性,选择在公共数据集VIPeR[23]、iLIDS[24]、CAVIAR[25]、3DPeS[26]上评测所提算法的效果。
实验中的特征提取及其他算法的参数设置参考文献[27]。实验随机选取p对行人图像作为训练集,余下的作为测试集,然后把以上产生训练集和测试集的过程重复10次,最后将10次实验结果的平均值作为最终实验结果。实验选择的核函数分别为linear、χ2和RBF-χ2。
实验中,为了与已有算法公正比较,采用CMC(cumulative match characteristic)曲线评价算法性能。CMC曲线描述的是在行人图像集中搜索待查询的行人,前r个搜索结果中找到待查询人的比率。第1匹配率Rank 1很重要,因为它表示完全正确的识别结果。当r取值较小时,前r个匹配率也较有现实意义。
3.1 VIPeR数据集VIPeR数据集包含632位行人的1 264张图像,每位行人有2张从不同摄像机拍摄的图像,每个图像尺寸都是128×48,在该数据集中同一个人的外观由于姿态、视角、光照和背景变化有很大差异。如图 1所示每一列中的行人图像为同一个人。实验中随机选取316对行人图像作为训练集,余下的316对行人图像作为测试集。

|
图 1 每列为来自2个摄像头下的同一个行人 Figure 1 The images from each column are captured from different cameras and belong to the same person |
表 1列出了该算法核映射前后的实验结果对比。从表 1可知,加入卡方核函数后,算法的识别率得到显著提升,尤其是基于RBF-χ2核函数算法的Rank1识别率比原始算法高出近10%。但是,其加入线性核函数后的算法识别率却比原始算法低,因为线性核函数是基于欧式距离来描述样本的不同,考虑的是各特征向量的绝对距离,而卡方核函数能够反映出各特征向量相对距离变化,根据每个特征量对分类结果贡献的不同,给出卡方距离下的样本向量权重,可有效提高算法的识别率。
| 表 1 核映射前后在VIPeR数据集上的实验结果 Table 1 Performance comparison between before and after the kernel map on the VIPeR dataset |
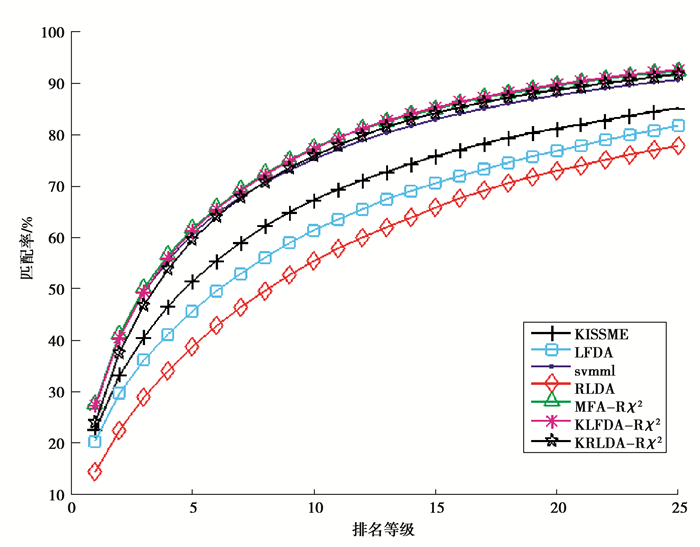
为了验证所提算法的有效性,将算法与当前主流的距离度量学习算法作对比实验,算法包括SVMML[28]、KISSME[29]、LFDA(local fisher discriminant analysis)[29]、MFA(marginal fisher analysis)[31]、KLFDA[27]。表 2列出了在VIPeR数据集上不同度量学习算法的实验对比结果,图 2给出了在VIPeR数据集上不同算法的CMC曲线。
|
图 2 在VIPeR数据集上不同算法的CMC曲线 Figure 2 CMC curves for different algorithms on the VIPeR dataset |
| 表 2 不同度量学习算法在VIPeR数据集上实验结果 Table 2 Experimental results of different algorithms on the VIPeR dataset |
从表 2可知,RLDA和KRLDA算法的识别率比MFA和KLFDA算法的要低,原因在于LDA在求解最佳投影矩阵时,很大程度会受到训练样本数量的影响。在VIPeR数据集上,由于每个行人的训练样本个数非常少,导致建立的散度矩阵不能很好地反映样本类内和类间变化,从而在很大程度上影响了算法性能,而MFA和KLFDA算法则保留了样本间的局部拓扑结构,通过构建样本间的局部邻近关系来获得最优投影矩阵,使样本在投影空间内具有更好的可分性,因此,其识别率要比本文算法的高。以下图表中的KLFDA、MFA和KRLDA算法的实验结果都是基于RBF-χ2核函数的。
3.2 iLIDS数据集iLIDS数据集包含119个行人的476张图像,每个行人拥有2到8张图像,由于该数据集是在机场收集,图像有严重的遮挡和光照变化问题,而且数据集中图像的尺寸也不一样,实验中把图像尺寸统一设置为128×48像素。实验中随机选择59对行人图像作为训练集,60对行人图像作为测试集。
表 3给出了算法核映射前后的实验结果对比,从表 3可知,在iLIDS数据集上经过核映射后基于χ2和RBF-χ2核函数的算法识别率整体上都得到明显提升,Rank1和Rank5最高提升了约5%和6%。
| 表 3 在iLIDS数据集上核映射前后实验结果 Table 3 Performance comparison between before and after the kernel map on the iLIDS dataset |
表 4给出了不同算法在iLIDS数据集上的实验对比结果,表中列出的KRLDA、MFA和KLFDA算法的实验结果都是基于RBF-χ2核函数。从表 4可知,所提的KRLDA算法的识别率更高,其Rank1比之前最好的算法提高了约2%。
| 表 4 不同算法在iLIDS数据集上的实验结果 Table 4 Experimental results of different algorithms on the iLIDS dataset |
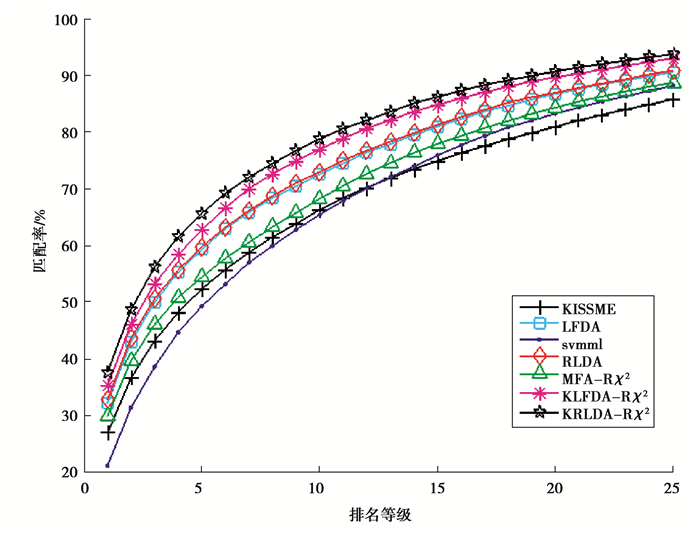
图 3给出了在iLIDS数据集上不同算法的CMC曲线图,如图所示,基于RBF-χ2核函数的KRLDA算法的整体效果要优于其他的算法。
|
图 3 在iLIDS数据集上不同算法的CMC曲线 Figure 3 CMC curves for different algorithms on the iLIDS dataset |
CAVIAR数据集由1 220张行人图像组成,包含72个行人,每个行人拥有10~20张图像。数据集中图像的尺寸不一致,实验时统一设置为128×48像素。实验中选择36对行人图像作为训练集,余下的36对行人图像作为测试集。
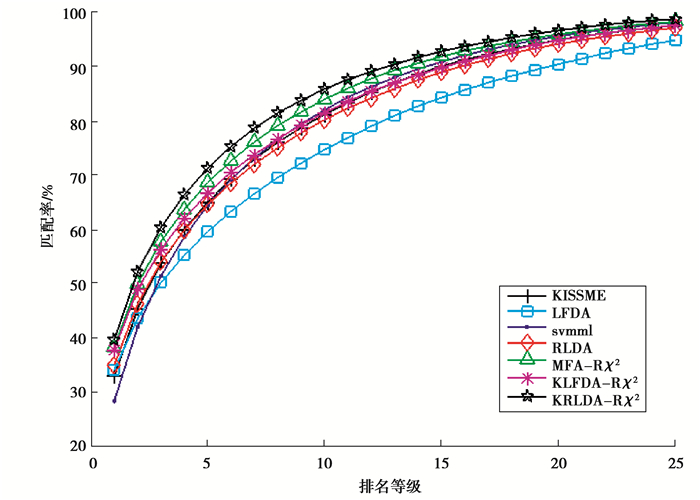
表 5给出了算法核映射前后的实验结果对比,基于RBF-χ2核函数的算法识别率比原始算法和基于线性核的算法高出约5%。表 6所示是在CAVIAR数据集上研究算法与其他算法的实验效果对比。图 4是在CAVIAR数据集上不同算法的CMC曲线图,如图所示,KRLDA算法优于其他的算法,表 6和图 4中的KLFDA、MFA和KRLDA算法的实验结果都是基于RBF-χ2核函数的。
|
图 4 在CAVIAR数据集上不同算法的CMC曲线 Figure 4 CMC curves for different algorithms on the CAVIAR dataset |
| 表 5 在CAVIAR数据集上核映射前后的实验结果 Table 5 Performance comparison between before and after the kernel map on the CAVIAR dataset |
| 表 6 不同算法在CAVIAR数据集上的实验结果 Table 6 Experimental results of different algorithms on the CAVIAR dataset |
3DPeS数据集是由8个非重叠的户外摄像头采集,包含192个行人的1 011张图像,每个行人有2~6张不等的图像。数据集中的图像尺寸不一致,实验中统一把图像尺寸设置为128×48像素。实验中随机选择97对行人图像作为训练集,余下的作为测试集。
表 7给出了算法核映射前后的实验结果对比,可以看出经过核映射后基于χ2和RBF-χ2核函数的算法识别率提升明显,其Rank1结果最高提升了约8%。
| 表 7 在3DPeS数据集上核映射前后的实验结果 Table 7 Performance comparison between before and after the kernel map on the 3DPeS dataset |
算法在3DPeS数据集上与其他算法的实验效果对比如下表 8,该算法在3DPeS数据集上的整体性能优于SVMML、KISSME、LFDA、RLDA和MFA算法,比KLFDA算法效果优但差距不明显。
| 表 8 不同算法在3DPeS数据集上的实验对比结果 Table 8 Experimental results of different algorithms on the 3DPeS dataset |
图 5表示在3DPeS数据集上不同算法的CMC曲线图,如图所示,KRLDA算法明显优于其他的算法,但与KLFDA算法效果接近。

|
图 5 在3DPeS数据集上不同算法的CMC曲线 Figure 5 CMC curves for different algorithms on the 3DPeS dataset |
在RLDA算法上加入了卡方核函数,提出了基于卡方核的正则化线性判别行人再识别算法(KRLDA)。该算法利用核函数将样本从线性不可分的原始特征空间映射到一个线性可分的高维特征空间,然后在高维空间中构造描述数据之间邻近关系的散度矩阵,利用正则化线性判别分析获得高维到低维空间的投影矩阵,使得数据在低维空间仍能够保持高维空间的可分性,从而提升行人再识别算法的识别率。
为了评价所提算法的性能,使用3个核函数(linear、χ2、RBF-χ2)并分别在VIPeR、iLIDS、CAVIAR、3DPeS 4个公共数据集上进行实验,而且,又分别与当前主流的行人再识别算法(KISSME、LFDA、KLFDA、SVMML、MFA)进行了比较实验。实验结果表明,卡方核函数较其他核函数识别率更高,经过卡方核映射后的识别率得到显著提升,而使用线性核函数后的识别率比原始算法略降低,并且在iLIDS、CAVIAR和3DPeS数据集上,基于RBF-χ2核算法的识别率要高于其他算法。但是,在VIPeR数据集上,由于训练样本个数非常少,采用保留样本间局部结构的算法(如KLFDA算法和MFA算法)识别率比研究算法更高。
| [1] |
Kviatkovsky I, Adam A, Rivlin E. Color invariants for person reidentification[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(7): 1622-1634. |
| [2] |
Yang Y, Yang J, Yan J, et al. Salient color names for person re-identification[C]//European Conference on Computer Vision. Switzerland: Springer, 2014: 536-551.
|
| [3] |
Rama V R, Wang G, Lu J. Learning invariant color features for person redentication[J]. IEEE Transactions on Image Processing, 2016, 25(7): 3395-3410. DOI:10.1109/TIP.2016.2531280 |
| [4] |
袁立, 田子茹. 基于融合特征的行人再识别方法[J]. 模式识别与人工智能, 2017, 30(3): 269-278. YUAN Li, TIAN Ziru. Pedestrian reidentification based on fusion feature[J]. Pattern Recognition and Artificial Intelligence, 2017, 30(3): 269-278. (in Chinese) |
| [5] |
杜宇宁, 艾海舟. 基于统计推断的行人再识别算法[J]. 电子与信息学报, 2014, 36(7): 1612-1618. DU Yuning, AI Haizhou. Pedestrian reidentification algorithm based on statistical inference[J]. Journal of Electronics & Information Technology, 2014, 36(7): 1612-1618. (in Chinese) |
| [6] |
Zheng W S, Gong S, Xiang T. Re-identification by relative distance comparison[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(3): 653-68. |
| [7] |
Chen D, Yuan Z, Hua G, et al. Similarity learning on an explicit polynomial kernel feature map for person re-identification[C]//Conference on Computer Vision and Pattern Recognition. USA: IEEE, 2015: 1565-1573.
|
| [8] |
Zhang Y, Li B, Lu H, et al. Sample-specific SVM learning for person re-identification[C]//Computer Vision and Pattern Recognition. USA: IEEE, 2016: 1278-1287.
|
| [9] |
Chen D, Yuan Z, Chen B, et al. Similarity learning with spatial constraints for person re-identification[C]//IEEE Conference on Computer Vision and Pattern Recognition. USA: IEEE, Computer Society, 2016: 1268-1277.
|
| [10] |
Farenzena M, Bazzani L, Perina A, et al. Person re-identification by symmetry-driven accumulation of local features[C]//Computer Vision and Pattern Recognition. USA: IEEE, 2010: 2360-2367.
|
| [11] |
Zheng W S, Gong S, Xiang T. Person re-identification by probabilistic relative distance comparison[C]//Computer Vision and Pattern Recognition. USA: IEEE, 2011: 649-656.
|
| [12] |
Zhao R, Ouyang W, Wang X. Unsupervised salience learning for person re-identification[C]//IEEE Conference on Computer Vision and Pattern Recognition. USA: IEEE Computer Society, 2013: 3586-3593.
|
| [13] |
Matsukawa T, Okabe T, Sato Y. Person re-identification via discriminative accumulation of local features[C]//201422nd Internationd Conference on Pattern Recognition. Stockholm, Sweden: IEEE, 2014, 43(3): 3975-3980.
|
| [14] |
Weinberger K Q, Saul L K. Distance metric learning for large margin nearest neighbor classification[J]. Journal of Machine Learning Research, 2009, 10(1): 207-244. |
| [15] |
Weinberger K Q, Saul L K. Fast solvers and efficient implementations for distance metric learning[C]//International Conference. Helsinki: ICML, DBLP, 2008: 1160-1167.
|
| [16] |
Davis J V, Kulis B, Jain P, et al. Information-theoretic metric learning[C]//International Conference on Machine Learning. USA: ICML, 2007: 209-216.
|
| [17] |
Guillaumin M, Verbeek J, Schmid C. Is that you? Metric learning approaches for face identification[C]//IEEE, International Conference on Computer Vision. Japan: IEEE, 2010: 498-505.
|
| [18] |
Friedman J. Regularized discriminant analysis[J]. Publications of the American Statistical Association, 2008, 84(405): 165-175. |
| [19] |
Chen L F, Liao H Y M, Ko M T, et al. A new LDA-based face recognition system which can solve the small sample size problem[J]. Pattern Recognition, 2000, 33(10): 1713-1726. DOI:10.1016/S0031-3203(99)00139-9 |
| [20] |
Hua Y, Jie Y. A direct LDA algorithm for high-dimensional data-with application to face recognition[J]. Pattern Recognition, 2001, 34(10): 2067-2070. DOI:10.1016/S0031-3203(00)00162-X |
| [21] |
Vapnik, Vladimir N. The nature of statistical learning theory[J]. Technometrics, 2002, 8(6): 1564-1564. |
| [22] |
Pele O, Werman M. The quadratic-chi histogram distance family[C]//European Conference on Computer Vision. Heraklion: Springer-Verlag, 2010: 749-762.
|
| [23] |
Gray D, Tao H. Viewpoint invariant pedestrian recognition with an ensemble of localized features[C]//Computer Vision-ECCV 2008. France: Springer Berlin Heidelberg, 2008: 262-275.
|
| [24] |
Zheng W S, Gong S, Xiang T. Associating groups of people[C]//British Machine Vision Conference. London, UK: BMVC, 2009: 1-11.
|
| [25] |
Dong S C, Cristani M, Stoppa M, et al. Custom pictorial structures for re-identification[C]//British Machine Vision Conference. Genova, UK: BMVC, 2011, 81: 1-11.
|
| [26] |
Baltieri D, Vezzani R, Cucchiara R. 3DPeS: 3D people dataset for surveillance and forensics[C]//Proceedings of the 2011 joint ACM workshop on Human Gesture and Behavior Understanding. USA: ACM, 2011: 59-64.
|
| [27] |
Xiong F, Gou M, Camps O, et al. Person re-identification using kernel-based metric learning methods[J]. Lecture Notes in Computer Science, 2014, 8695: 1-16. DOI:10.1007/978-3-319-10584-0 |
| [28] |
Li Z, Chang S, Liang F, et al. Learning locally-adaptive decision functions for person verification[C]//IEEE Conference on Computer Vision and Pattern Recognition. USA: IEEE Computer Society, 2013: 3610-3617.
|
| [29] |
Hirzer M. Large scale metric learning from equivalence constraints[C]//IEEE Conference on Computer Vision and Pattern Recognition. USA: IEEE Computer Society, 2012: 2288-2295.
|
| [30] |
Pedagadi S, Orwell J, Velastin S, et al. Local fisher discriminant analysis for pedestrian re-identification[C]//IEEE Conference on Computer Vision and Pattern Recognition. USA: IEEE Computer Society, 2013: 3318-3325.
|
| [31] |
Yan S, Xu D, Zhang B, et al. Graph embedding and extensions:A general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 29(1): 40-51. |
 2018, Vol. 41
2018, Vol. 41


