在智能电网的实时监测系统中，随着智能设备、智能表计和智能终端等广泛使用，细粒度测量使用户隐私泄露问题越加的严重^[1-2]。从传感器收集实时测量可以推断出用户的行为隐私，虽然细粒度的测量不能直接访问，但仍可以通过现有的差分攻击从实时聚合的动态序列中推断出详细测量。为了使用户隐私得到有效保护，一般采用加密和加噪2种方式实现^[3]，虽然加密方式可以有效实现数据的完整性和机密性，但机密性不等于隐私性且开销较高。因此，将采用更为高效，成本较低的加噪方式实现隐私保护。

Anandan B等人提出了一种简单的拉普拉斯噪声算法(SLN, simple laplacian noise algorithm)^[4]，该算法根据给定的全局敏感度来直接添加拉普拉斯噪声，通过噪声扰动的方式，使用户数据与噪声之间不易区分，有效避免了隐私泄露。但由于全局敏感度较高，使所添加的噪声幅度增大，导致隐私保护效用降低以及噪声方差增加。Geng Q等人提出一种均匀拉普拉斯噪声算法(ULN, uniform laplacian noise algorithm)^[5]，该算法具有等概率的噪声分布，即每个维度所添加噪声一致，有效实现了数据隐私保护，但其效能性依然无法达到最优。

在SLN算法和ULN算法研究基础上，提出一种基于多维分解的拉普拉斯噪声算法(MDLN, multi-dimensional laplacian noise algorithm)，该算法将原始测量值分解成多维数据，计算各维度的隐私敏感度，并根据相应的敏感度自适应决定需添加的拉普拉斯噪声幅度，针对高相关性和高度波动的时间序列数据，通过噪声扰动方式可以有效实现差分隐私。通过与SLN算法和ULN算法仿真相比较，MDLN算法的隐私保护强度较高，且效能更高。

1 模型建立 1.1 模型构建

在简单的拉普拉斯噪声算法中，由于给定的全局敏感度较高，使整体需添加的拉普拉斯噪声较大，从而导致噪声方差增加以及数据效能下降。因此，在满足差分隐私前提下，根据输出函数的各维度敏感度来自适应计算需添加的拉普拉斯噪声，以提高数据效能是至关重要的，即采用降低敏感度的方式来提高数据效能。

模型建立如下：在实时的监测系统中，传感器部署在用户端以完成数据采集监测，并将实时测量的数据传送到集中式服务器，服务器对接收到的数据进行统计分析，即针对个体用户的时间序列进行聚合^[6-7]。假设传感器仪表是值得信赖的设备，且传感器仪表与集中式服务器之间的通信通道安全可靠。现假定一个单变量的离散时间序列X={x_k}表示为时隙k的实时测量数据，且第t个时隙实时聚合表示为${r_\mathit{t}} = \sum {_{k = 1}^t} {x_\mathit{k}} $，即从第1时隙到t时隙的用户时间序列测量累积和。研究所使用的符号列于表 1如下所示。

1.2 差分隐私定义

差分隐私(DP，differential privacy)是一种基于数据失真的隐私保护技术，即通过随机噪声的添加使敏感数据失真，同时保持某些数据或数据属性不变，处理后的数据仍然具有一定的统计特性^[8]。

假设ε为指定的隐私保护预算，该参数通常用来控制算法在2个邻近数据集上获得相同输出的概率比值。通常情况下，ε取值较小^[9]，因为当ε减小时，隐私保护强度增加，当ε=0时，隐私保护强度达到最高，此时可以保证算法输出的任意相邻数据集都具有相同的概率分布。因此，ε—差分隐私可以保证具有相同输出的2个相邻数据集的概率非常接近，使概率扩展受到exp(ε)界限，以致于攻击者几乎不能通过操纵输出来推断单个数据记录^[10-11]。

为了实现ε—差分隐私，提出将正确校准的拉普拉斯噪声添加到输出值，使攻击者无法判断噪声与数据之间的差别。已知拉普拉斯噪声由具有概率密度函数${\rm{Lap(}}\mathit{\lambda }{\rm{) = }}\frac{1}{{2\mathit{\lambda }}}{\mathit{e}^{\mathit{ - }\left| x \right|/\lambda }}$的拉普拉斯分布所绘制，其中参数λ由全局敏感度GS_f和隐私预算ε决定，即λ=GS_f/ε^[12-13]。全局敏感度GS_f定义为2个相邻数据集输出的最大差值，是决定噪声量添加大小的参数，通常表示为实数值，若为浮点数，则可以转换为实数。

2 MDLN算法 2.1 算法分析

为了实现高隐私保护强度和高数据效能，提出一种多维分解的拉普拉斯噪声算法(MDLN)，算法将输出实数分解成有界数的几个加权维度，并根据给定的全局敏感度g，隐私保护预算ε和界值b，计算获得随机屏蔽噪声r，其算法流程如下所示

算法：多维分解拉普拉斯噪声算法MDLN

输入：全局敏感度g，界值b和隐私保护预算ε

输出：随机噪声r

1：计算维数$d = \left\lfloor {{{\log }_b}\mathit{g}} \right\rfloor + 1 $

2：if维数d=1 then

3：维度敏感度是s₁=g

4：else

5：指定低于d-1维度的敏感度为s_i=b-1(i=1, 2, …, d-1)，计算最高维度的敏感度为${s_\mathit{d}} = \left\lfloor {\frac{g}{{{b^d} - 1}}} \right\rfloor $

6：end if

7：根据具有参数s_i和ε的拉普拉斯噪声分布${\rm{Lap}}\left( {\frac{{{s_i}}}{\varepsilon }} \right) $产生d个独立噪声m_i(i=1, 2, …, d)

8：产生随机噪声r，即$r \leftarrow \sum {_{i = 1}^d} {m_i}{b^{i - 1}}$

根据以上算法流程，进一步说明如下

1) 根据给定的全局敏感度g、界值b(2≤b≤g)和隐私保护预算ε，自适应计算出维度d，计算公式为：$d = \left\lfloor {{{\log }_\mathit{b}}g} \right\rfloor + 1$。

2) 通过界值b可以指定多维度的权重：假设b=10，则可以看作是十进制分解；b=8，则为八进制分解；b=2，则是二进制分解，则第i维度的权重w_i=2^i-1。

3) 通过界值b引入d个维度中各维度的敏感度s_i(i=1, 2, …, d)，低于d-1维度的敏感度s_i=b-1(i=1, 2, …, d-1)，第d维度的敏感度${s_\mathit{d}} = \left\lfloor {\frac{g}{{{b^d} - 1}}} \right\rfloor $，且$\left\lfloor {\frac{g}{{{b^d} - 1}}} \right\rfloor < b - 1$。然后根据各维度的敏感度自适应调整需添加的拉普拉斯噪声幅度，并生成所有维度的屏蔽噪声r。

4) 根据所绘制的拉普拉斯分布${\rm{Lap}}\left( {\frac{{{s_i}}}{\mathit{\varepsilon }}} \right)$，决定各维度需添加的独立噪声m_i(i=1, 2, …, d)，在所有d维度上实现差分隐私。

5) 最后，将各维度的相应权重w_i=b^i-1与独立噪声m_i线性结合，得到整体掩蔽噪声$r = \sum {_{i = 1}^d} {m_i}{b^{i - 1}}$，掩蔽噪声r可用于实现总体差分隐私。

6) 当b≥g+1时，维度数d=1，则维度敏感度应为s₁=g。此时，MDLN算法降解为简单的拉普拉斯噪声算法SLN。

对于每个维度，基于拉普拉斯噪声机制计算添加的噪声m_i以实现差分隐私，根据平行组合定理，在不同维度的不相交子集上计算所有噪声，平行组合可以满足差分隐私^[14]。根据并行组合定理，所有独立维度的组合输出仍然可以保证相同水平的差分隐私。

2.2 MDLN隐私分析

针对MDLN算法的差分隐私进行分析，即定理如下

定理1：MDLN算法满足ε-差分隐私。

证明：将C表示为MDLN算法的多维分解，C_i表示第i维的分解输出，v表示为观察值，v_i表示每个维度的分解结果。根据MDLN算法，各维度输出C_i和v_i(i=1, 2, …, d-1)应在范围[0, b-1]内，C_d和v_d应在[0，s_d]内。每个维度通过添加校准拉普拉斯噪声${\rm{Lap(}}\mathit{\lambda }{\rm{) = }}\frac{1}{{2\lambda }}{\mathit{e}^{\mathit{ - }\left| x \right|/\mathit{\lambda }}}$来满足ε-差分隐私，其中λ=Δf/ε且Δf表示全局敏感度，噪声δ(x)与exp(-ε|x|/Δf)成比例。

在组合中，分解的维度具有不同的权重w_i=b^i-1，因此每个维度值应该被缩放为新的变量Y_i=b^i-1C_i(S)。则组合后的测量值S=Y₁+Y₂+…+Y_d的敏感度为$\Delta \mathit{f = }\sum {_{i = 1}^{d - 1}(\mathit{b} - 1)} {b^{i - 1}} + {s_d}{b^{d - 1}} = {b^{d - 1}} + {s_d}{b^{d - 1}} - 1 $。假设在d个维度上相邻测量值S′由d个独立测量Y′₁, Y′₂, …, Y′_d组成，可以得到Y′_i=w_iC_i(S′)。在每个维度上，第i维上的变量Y_i和Y′_i应该遵循关系$\mathit{Pr}{\rm{[}}{\mathit{Y}_\mathit{i}}{\rm{] = }}\mathit{Pr}{\rm{[}}\mathit{Y}_i^\mathit{'}{\rm{]}} \times {\rm{exp}}\left( {\frac{\mathit{\varepsilon }}{{\Delta \mathit{x}}}\left| {{Y_i} - Y_i^\mathit{'}} \right|} \right) = \mathit{Pr}{\rm{[}}\mathit{Y}_i^\mathit{'}{\rm{]}} \times \exp \left( {\frac{{{b^{i - 1}}}}{{\Delta f}}\left| {{C_i} - C_i^\mathit{'}} \right|} \right) $，应该注意的是|C_i-C_i^′|≤b-1以及|C_d-C_d^′|≤s_d。使用上述差分隐私的关系和定义，假设有2个测量值S和S′，通过MDLN算法分别分解为d个维度测量值Y_i=w_i·C(S)和Y_i^′=w_i·C(S′)，并且在每个维度添加噪声之后，S和S′将映射到具有d维度相同的测量值v和v_i，则

$\begin{array}{l} \mathit{\;\;\;\;\;\;\;\;Pr}{\rm{[}}\mathit{C}{\rm{(}}\mathit{S}{\rm{) = }}\mathit{v}{\rm{] = }}\prod\limits_{i = 1}^d {\mathit{Pr }} [{\mathit{Y}_\mathit{i}} = {\mathit{v}_\mathit{i}}] = \prod\limits_{i = 1}^d {\mathit{Pr}} [{\mathit{w}_\mathit{i}}{\mathit{C}_\mathit{i}}(\mathit{S}) = {\mathit{v}_\mathit{i}}] = \\ \prod\limits_{i = 1}^d {\mathit{Pr}} [{\mathit{w}_\mathit{i}}{\mathit{C}_\mathit{i}}(\mathit{S'}) = {v_i}] \times \prod\limits_{i = 1}^d {\exp \left( {\frac{\mathit{\varepsilon }}{{\Delta \mathit{f}}} \times {\mathit{w}_\mathit{i}}\left| {{C_i}(\mathit{S}) - {\mathit{C}_\mathit{i}}(\mathit{S'})} \right|} \right)} = \\ \prod\limits_{i = 1}^d {\mathit{Pr}{\rm{[}}{\mathit{w}_\mathit{i}}{\mathit{C}_\mathit{i}}{\rm{(}}\mathit{S'}{\rm{) = }}{\mathit{v}_\mathit{i}}{\rm{]}}} \times \prod\limits_{i = 1}^{d - 1} {\exp \left( {\frac{\mathit{\varepsilon }}{{\Delta f}} \times {b^{i - 1}}\left| {{C_\mathit{i}}\left( S \right) - {C_i}(\mathit{S'})} \right|} \right)} \times \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;exp}}\left( {\frac{\mathit{\varepsilon }}{{\Delta f}} \times {b^{d - 1}}\left| {{C_d}(\mathit{S}) - {\mathit{C}_\mathit{d}}(\mathit{S'})} \right|} \right) = \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}\prod\limits_{i = 1}^d {\mathit{Pr}} [{\mathit{w}_\mathit{i}}{\mathit{C}_\mathit{i}}(\mathit{S'}) = {\mathit{v}_\mathit{i}}] \times exp(\frac{\mathit{\varepsilon }}{{{b^{d - 1}} + {s_d}^{b - 1} - 1}} \times \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}\sum\limits_{i = 1}^{d - 1} {\left( {{b^{i - 1}}\left| {{C_\mathit{i}}(\mathit{S}) - {\mathit{C}_\mathit{i}}(\mathit{S'})} \right|} \right)} ) \times \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;exp}}\left( {\frac{\mathit{\varepsilon }}{{{b^{d - 1}} + {s_d}{b^{b - 1}} - 1}} \times {b^{d - 1}} + {s_d}{b^{d - 1}} - 1} \right) \le \prod\limits_{i = 1}^d {\mathit{Pr}\left[ {{\mathit{w}_\mathit{i}}{C_\mathit{i}}(\mathit{S'}) = } \right]{v_i} \times } \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;exp}}\left( {\frac{\mathit{\varepsilon }}{{{b^{d - 1}} + {s_d}{b^{d - 1}} - 1}} \times \left( {{b^{d - 1}} + {s_d}{b^{d - 1}} - 1} \right)} \right) = \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}\prod\limits_{i = 1}^d {\mathit{Pr}} \left[ {{\mathit{w}_\mathit{i}}{C_\mathit{i}}(\mathit{S'}) = {\mathit{v}_\mathit{i}}} \right] \times \exp (\varepsilon ) = {\rm{ }}\\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}\mathit{Pr}{\rm{[}}{\mathit{C}_\mathit{i}}\left( {\mathit{S'}} \right){\rm{ = }}\mathit{v}{\rm{]}} \times \exp \left( \mathit{\varepsilon } \right) \end{array} $

(1)

由以上可知，在MDLN算法中映射到相同测量v的2个测量S和S′是不可区分的。因此，MDLN算法满足ε—差分隐私。

2.3 MDLN效能分析

针对MDLN算法的效能进行分析，已知通过MDLN算法可以获得掩蔽噪声的分布特征。首先，对满足ε-差分隐私的SLN算法掩蔽噪声的方差表示为

${V_{{\rm{SLN}}}} = 2{\left( {\frac{g}{\mathit{\varepsilon }}} \right)^2}, $

(2)

其中全局敏感度g满足以下不等式

${b^{2\left( {d - 1} \right)}} \le {g^2} \le {\left( {{b^d} - 1} \right)^2}。$

(3)

然后，对MDLN算法中噪声的预期值和方差详细分析如下：首先，每个维度上所加噪声都遵循拉普拉斯分布，即m_i~Lap(s_i/ε)，且每个噪声的预期值为0，这些噪声彼此独立。因此，预期值为0的d个独立噪声线性组合后掩蔽噪声r的预期值仍为0。已知m_i~Lap(s_i/ε)，根据拉普拉斯分布特征，噪声方差为$2{\left( {\frac{{{s_i}}}{\mathit{\varepsilon }}} \right)^2} $。因为维度权重表示为b^i-1，则维度方差为${\mathit{v}_\mathit{i}} = {b^{2(i - 1)}} \times 2{\left( {\frac{{{s_i}}}{\mathit{\varepsilon }}} \right)^2}$。根据噪声的独立性，组合输出r的方差V应该是d个噪声值m_i的方差总和。可以得到

$V = \sum\limits_{i = 1}^d {{v_i}} = \sum\limits_{i = 1}^d {{b^{2\left( {i - 1} \right)}}} \times 2{\left( {\frac{{{s_i}}}{\mathit{\varepsilon }}} \right)^2} = \sum\limits_{i = 1}^d {{{\left( {{b^{(\mathit{i} - 1)}}{\mathit{s}_\mathit{i}}} \right)}^2}} \times 2{\left( {\frac{1}{\mathit{\varepsilon }}} \right)^2}, $

(4)

其中s_i≤b-1。

现定义有利比率(FR，favorable ratio)来显示MDLN算法与SLN算法相比的有效性，以及ULN算法与SLN算法相比的有效性，定义如下

定义1(有利比率)：当给定相同的全局敏感度g和隐私保护预算ε，计算MDLN算法比SLN算法输出较少的噪声方差的概率，以及ULN算法比SLN算法输出较少噪声方差的概率。现在对MDLN算法的效能分析描述如下

首先全局敏感度g满足以下不等式

$n{b^{d - 1}} \le g \le \left( {n + 1} \right){b^d} - 1, \ $

(5)

${n^2}{b^{2(\mathit{d} - 1)}} \le {g^2} < {\left( {n + 1} \right)^2}{b^{2d}}, \left( {n = 1, 2, \cdots , b} \right), $

(6)

且相应的方差表示为

$\begin{array}{l} {V_{{\rm{MDLN}}}} = \sum\limits_{i = 1}^d {{b^{2\left( {i - 1} \right)}}} \cdot 2{\left( {\frac{{{s_i}}}{\varepsilon }} \right)^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^{d - 1} {{b^{2\left( {i - 1} \right)}}} \cdot 2{\left( {\frac{{b - 1}}{\mathit{\varepsilon }}} \right)^2} + {b^{2(\mathit{d} - 1)}} \cdot 2{\left( {\frac{{{s_d}}}{\varepsilon }} \right)^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^{d - 1} {{b^{2\left( {i - 1} \right)}}} \cdot 2{\left( {\frac{{b - 1}}{\mathit{\varepsilon }}} \right)^2} + {b^{2\left( {d - 1} \right)}} \cdot 2{\left( {\frac{n}{\mathit{\varepsilon }}} \right)^2} \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\sum\limits_{i = 1}^d {{b^{2\left( {i - 1} \right)}}} } \right)2{\left( {\frac{{b - 1}}{\mathit{\varepsilon }}} \right)^2} \le 2{\left( {\frac{g}{\mathit{\varepsilon }}} \right)^2}, \end{array} $

(7)

其中MDLN算法的噪声方差远小于SLN算法，显示出更好的效能。

此外，将L和l分别定义为间隔[n²b^2(d-1), (n+1)²b^2d]和$\left[ {\frac{{\left( {b - 1} \right)\left( {{b^{2(d - 1)}} - 1} \right)}}{{b + 1}} + {n^2}{b^{2(d - 1)}},{{(n + 1)}^2}b2d} \right]$的长度，且定义比率l/L表示MDLN算法的有利比率。可以得到

$\mathop {\lim }\limits_{d - > \infty } fr\left( {b, d} \right) = \mathop {\lim }\limits_{d - > \infty } \frac{l}{L} = \frac{{{b^3} - 3}}{{\left( {b + 1} \right)\left( {{b^2} - 1} \right)}}, $

(8)

$\mathop {\lim }\limits_{d - > \infty } fr\left( {b, d} \right) = \mathop {\lim }\limits_{d - > \infty } \frac{l}{L} = 1\left( {b, d \in {N^ + }} \right)。$

(9)

从上式可以看出，MDLN算法的有利比率将随界值b和维度d的增长而增长，最终趋向于1，且界值b将增加时，维度d将减小。

3 仿真分析

为了验证相比ULN算法和SLN算法，MDLN算法在隐私保护强度和效能上达到最优，需对仿真参数进行设定。首先，假定一个智能计费系统场景，住宅智能电表将定期收集用户用电量的实时测量值，累计用户的用电量，并将实时汇总返回系统服务器进行结算^[15]。根据Richardson等人开发的模拟器生成的电量使用数据^[16]，随机选择了不同家庭大小，不同家用电器和不同占用模式的用户一天用电量数据进行仿真，所有测量值将被预处理为整数，浮点数也可以转换为整数。现设全局敏感度g的范围为1到2 000，差异隐私保护预算ε=2，参数b可取不同的值，

在仿真比较中，将采用噪声分布和数据相邻位的相对斜率来间接表示3种算法的隐私保护强度。相对斜率由相邻位之间频率比计算可得，即通过exp(ε)=1+ε反映隐私保护强度，相对斜率与1之间的最大绝对差即显示了隐私保护预算ε。当相对斜率为1时，表示ε=0且相邻位之间具有完全相同的隐私概率。当相对斜率比1大出(1+ε)或比1小出(1-ε)时，表示隐私保护强度较低。采用噪声方差和有利比率来间接表示3种算法的效能性, 见公式(7)-(9)。

1) 隐私保护强度分析

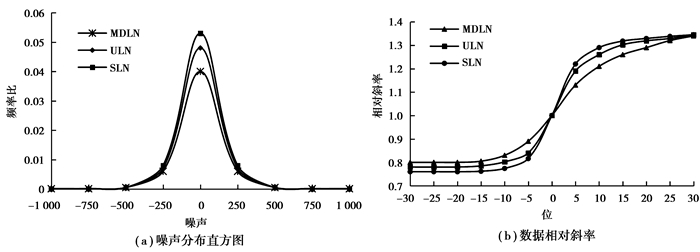
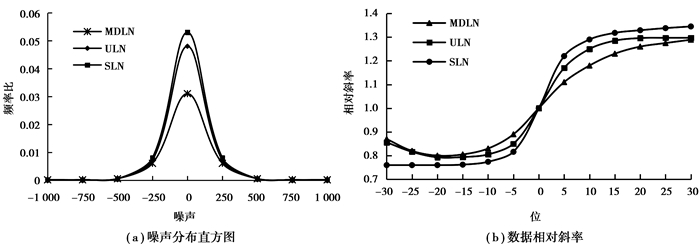
为了表征MDLN算法，ULN算法和SLN算法的隐私保护强度，采用噪声分布和数据相邻位的相对斜率间接表示。如图 1(a)和图 2(a)所示，显示了MDLN算法，ULN算法和SLN算法的噪声分布结果。从图中看出，相比SLN算法和ULN算法，MDLN算法的噪声分布更加紧凑，且频率比较低，表示该噪声具有更高的集中性和效能性。如图 1(b)和图 2(b)所示，显示了MDLN算法，ULN算法和SLN算法在数据相邻位的相对斜率。从图中看出，相比SLN算法和ULN算法，MDLN算法的相对斜率在负半轴中较大，在正半轴中较小，表示MDLN算法的相邻测量值之间的噪声差异较小。对比SLN算法和ULN算法，MDLN算法的隐私保护强度更好。

2) 效能分析

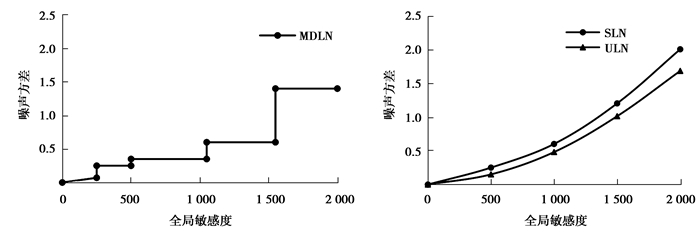
为了表征MDLN算法，ULN算法和SLN算法的效能性，采用噪声方差和有利比率来间接表示。如图 3所示，显示了MDLN算法，ULN算法和SLN算法噪声方差随全局敏感度的变化示意图。从图中可以看出，随着全局敏感度的增加，MDLN算法，ULN算法和SLN算法的噪声方差逐渐增加，且ULN算法的噪声方差小于SLN算法的噪声方差。对比SLN算法和ULN算法，MDLN算法的噪声方差达到最小。

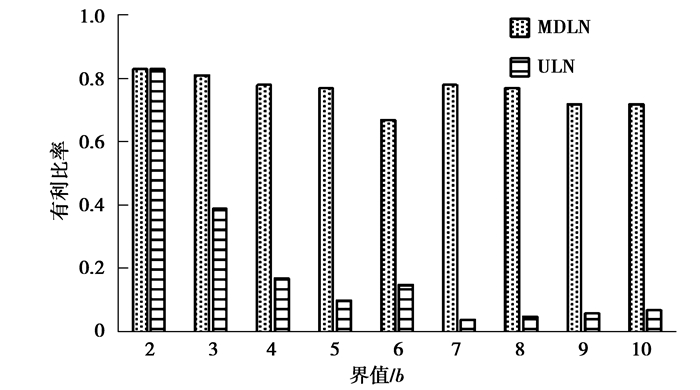
如图 4所示，显示了MDLN算法和ULN算法有利比率随界值b的变化示意图(g=2 000)。从图中可以看出，随着b值的增加，ULN算法的有利比率逐渐下降(波动是由界值b相对较小时，分解后维度d增大所引起)，而MDLN算法的有利比率均大于0.5。可以得出，当给定的界值b较大时，分解后的维度d下降，此时所有维度都具有更高效的噪声覆盖。在MDLN算法中，由于最高维度敏感度小于界值b，因此屏蔽噪声的效率更高。相比ULN算法，MDLN算法的数据效能性更高。

4 结论

为解决智能电网中用户隐私泄露问题，实现用户数据的完整性和强安全性，笔者提出一种基于多维分解的拉普拉斯噪声算法(MDLN)，该算法对用户的电能数据进行聚合，并根据给定的界值对聚合后的原始数据进行分解，计算分解后各维度的隐私敏感度，根据敏感度自适应添加拉普拉斯噪声，通过验证，该算法可以有效的实现差分隐私。仿真表明，与SLN算法和ULN算法相比较，MDLN算法的隐私保护强度较高，且效能更高。鉴于隐私特性，该算法同样适用于其它弱终端无线传感网的监测系统。