振动沉桩技术具有低噪音、低震感、机动性强等优点,不仅可以沉拔混凝土预制桩、各类型钢板桩,还可以用于振动沉拔大直径钢管桩的施工[1]。近年来,大直径管桩在实际工程中得到越来越广泛的应用[2]。但在实际工程中,大多是根据经验或半经验方法预测管桩贯入速率,所以,研究管桩振动贯入机理对于更好地预测管桩贯入速率,分析管桩的可打入性及贯入最大深度,实现管桩贯入施工控制,具有非常重要的实际意义。
为了分析打桩的能力、计算打桩的贯入速率、确定最终的贯入深度,多位学者利用理论解析方法进行了一系列振动打桩模型研究。Holeyman[3]提出“运动规律的积分模型”,该模型可分析单个循环周期内桩的加速率。Vanden[4]假定桩为刚体,将土体划分为系列同心轴的圆环柱体,提出了“Vipere模型”。通过模型计算结果与现场试验数据相比较,验证了“Vipere模型”在实际打桩工程应用中的可靠性。Salgado[5]在“Vipere模型”基础上,将土层划分为系列同心圆盘,分别建立桩侧、桩端与土体的接触模型,用于模拟桩的贯入过程。理论解析法存在较多局限性,如计算模型假设管桩与土体始终保持接触,不能考虑浅层土体沉陷的影响;打桩模型适用于均质土层,很难准确计算管桩贯入非均质土层的贯入速率。
除理论解析法外,国内外学者也进行了一系列的模型实验。Viking[6]对钢板桩高频振动贯入非粘性土进行大量现场足尺试验,分析了桩贯入速率的影响因素。王伟[7]对不同物理性质的土进行振动沉桩试验,研究土体相对密实度、饱和度与振动沉桩效率之间的关系。由于模型试验存在无法忽略的边界效应与扰动影响的问题,研究成本较高,不能广泛应用。
运用ABAQUS软件,建立大直径钢管桩振动贯入全过程的数值模型,对管桩贯入速率、贯入阻力进行了研究;同时,分析了静载力与动载力比值对贯入速率的影响,结论对管桩的设计和施工具有一定的参考价值。
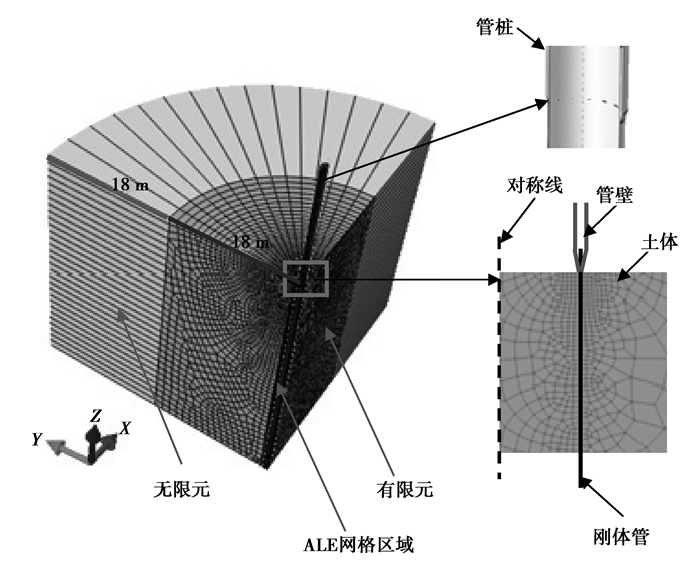
1 分析模型与方法 1.1 几何模型采用ABAQUS/Explicit建立钢管桩振动贯入砂土的数值模型。管桩长L=18 m,外径D=1 m,壁厚为2 cm。管桩与近场域土体采用有限元模拟,有限元网格采用8节点实体减缩积分单元。为了消除振动波反射的影响,远场域土体采用无限元模拟,无限元网格采用8节点实体无限单元,有限元分析模型网格如图 1所示。打入的管桩采用离散刚体单元模拟,不考虑管桩变形。为解决管桩高频振动贯入过程中管桩周围土体大变形和网格畸变等问题,管桩附近1 m范围内的土体单元采用任意拉格朗日-欧拉(ALE)自适应网格划分技术。参考文献[8]的建模方法,沿管桩壁建1个壁厚1 mm的刚体管(见图 1),建立管壁和土的接触。管桩贯入前,管桩与周围土体设为无摩擦;管桩贯入过程中,管桩沿刚体管滑动,土与刚体管分开。采用这种方法,可建立贯入管桩与周围土体之间的接触。管壁与土体的接触采用Coulomb摩擦接触模型,刚体管和土设为光滑硬接触。桩-土接触面间的摩擦系数μ与土体内摩擦角φ相关,摩擦系数公式[9]
|
图 1 有限元模型 Figure 1 Finite element model |
管桩振动贯入的激振力采用力控制模拟,其中,静态荷载F0=100 kN,动力荷载幅值Fc=2 700 kN,振动频率f=27.5 Hz,激振力Fd=F0+Fcsin(2πft)。
只研究机理性状,采用均质土层,土体有限元部分采用Mohr-Coulomb弹塑性模型。由于砂性土透水性强,极短时间内管桩周围土体的孔压消散完毕。管桩贯入过程中,周围土体主要处于静孔隙水压力状态。因此,有限元分析不考虑超孔隙水压力的问题,采用有效应力指标分析,具体参数见表 1。
| 表 1 砂土参数 Table 1 Parameters of sands |
材料阻尼的大小会影响管桩高频振动贯入过程中振动波的传播过程,阻尼越小,振动波衰减得越慢。ABAQUS提供的瑞利材料阻尼由质量比例阻尼αβ和刚度比例阻尼βR组成。由于有限元区域土体施加了边界约束,不会产生绝对运动,数值模型只需考虑刚度比例阻尼βR,其表达式为
| ${\mathit{\beta }_{\rm{R}}} = 2{\rm{ \mathit{ ξ} /}}{\mathit{\omega }_{\rm{1}}}, $ | (1) |
式中:ξ为阻尼系数;ω1为第一阶固有频率。土体ω1取1.23 Hz,阻尼系数选用Ekanayake[10]的推荐值ξ=2%,由公式(1)得βR=0.033。
1.3 模型验证将文中数值结果与现场实测结果进行比较,验证所建立的管桩振动贯入数值模型的可靠性。
拟建工程为某住宅小区,6幢14~16层住宅,采用框架剪力墙结构,总建筑面积为76 000 m2。采用直径1 000 mm全套管取土灌注桩,桩端持力层为中风化花岗岩,单桩竖向承载力特征值3 360 kN。场地土层自上而下分别为:1)杂填土,厚度为0.90~2.20 m;2)中砂,厚度为2.10~13.50 m,由于未获得砂土具体参数,砂土参数按表 1取值;3)全风化花岗岩,厚度为1.20~2.35 m;4)中风化花岗岩,厚度为3.60~7.10 m。采用美国APE200-6高频液压振动锤进行套管(即钢管桩)高频振动贯入,静态荷载F0为100 kN,动力荷载幅值Fc为2 700 kN,振动频率f为27.5 Hz。
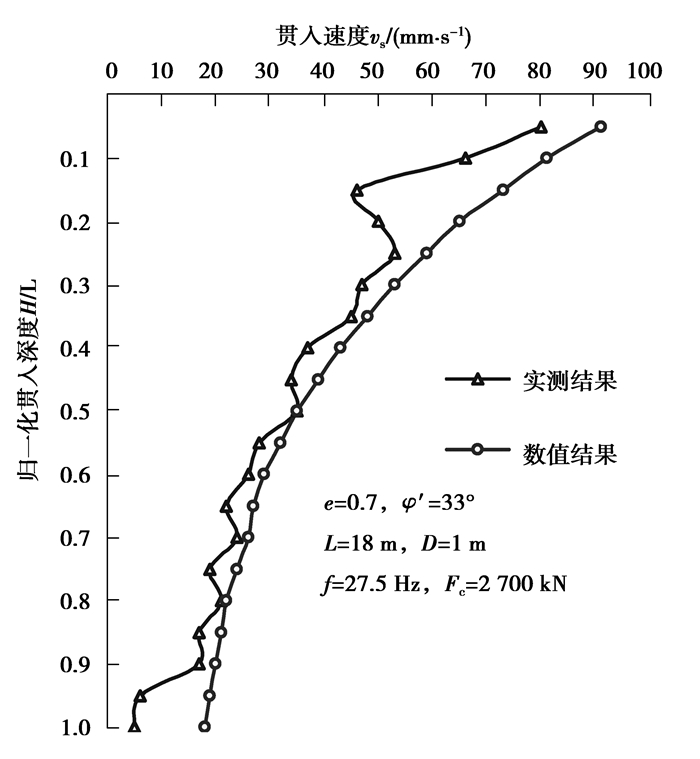
图 2为贯入速率的数值结果与实测结果比较。研究发现:1)管桩贯入深度较浅时,数值结果与实测结果存在较大误差,实测结果明显小于数值结果。产生这种误差的原因可能有2个:一是实测场地地表处存在1.3 m厚的杂填土,粒径5~10 cm的块石阻碍了管桩的贯入;二是在管桩贯入初期,为了确保孔位的准确性,通过人为控制减缓了管桩的贯入速率。2)管桩贯入深度较深时,实测结果与计算结果的误差相对减小,但仍存在一定的离散性。这主要是由于文中数值模型假设土体为均质砂土层,而实测场地深层土体为颗粒级配差的中砂层。3)管桩贯入后期,在土层分界面上,实测结果的贯入速率产生了突变,这是管桩贯入导致全风化花岗岩层的缘故。因此,当管桩贯入的砂土地基较为均质时,文中数值模型结果与实际贯入速率基本吻合。
|
图 2 贯入速率的实测结果与数值结果比较 Figure 2 Comparison between measured results and numerical results for the penetration speed |
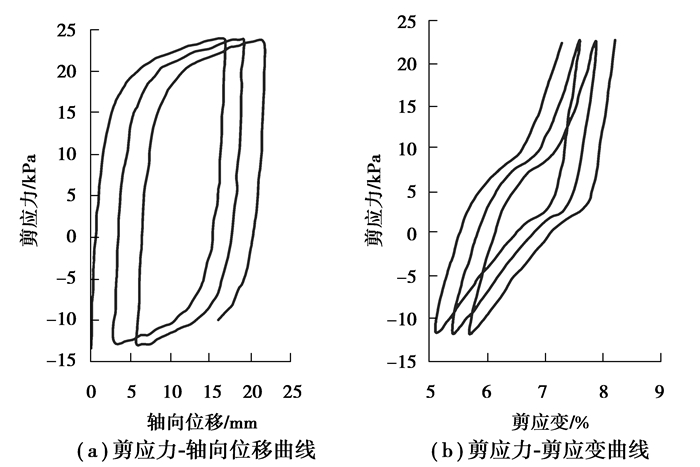
图 3为贯入深度9 m处管侧土体剪应力曲线。由图可知,1)管侧土体随着管桩的运动产生循环反复的剪切应力,与Lee等[11]试验得到的钢板桩振动贯入砂土过程中的桩侧土体剪应力轴向位移曲线规律一致;2)管侧土体剪应力剪应变滞回曲线为典型的“香蕉”形,与Vanden[4]的试验结果相似。除了第1个循环外,其余的循环均很好地形成了封闭回路。每个循环的滞回曲线均由2个剪胀阶段和2个剪缩阶段组成,能直观地反映出管壁与土体间的反复剪切作用。
|
图 3 管侧土体剪应力曲线(贯入深度9 m) Figure 3 soil shear stress curves (penetration depth is 9 m) |
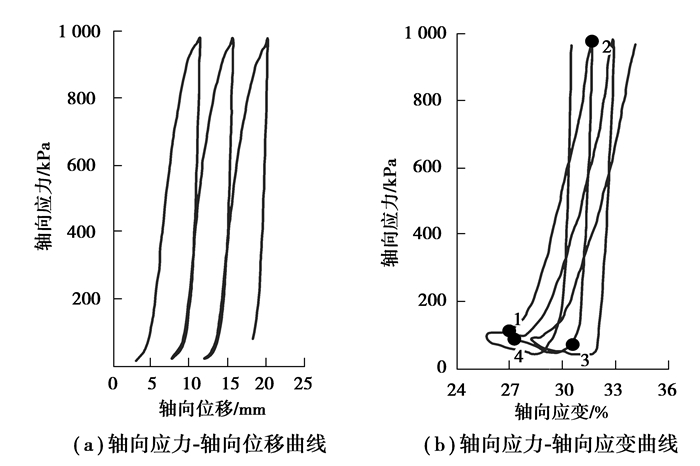
图 4为贯入深度9 m处管端土体轴向应力曲线。由图 4可知,1)管端土体在管桩的作用下处于循环反复的加卸载状态,与Cudmani等[12]模拟桩振动贯入砂土过程中桩端土体的轴向应力轴向位移曲线规律相似。2)管端土体轴向应力剪应变滞回曲线为典型的“镰刀”形,与Vanden[4]的研究结果相吻合。管端土体经历2个显著的压缩阶段和拉伸阶段。当管桩向下运动时,管端土体轴向应力迅速增加(1~2部分),当管桩的位移方向开始改变时(点2),管端土体轴向应力快速减小到一个低值(2~3部分),并且在接下来的压缩阶段和拉伸阶段基本保持不变。
|
图 4 管端土体轴向应力曲线(贯入深度9 m) Figure 4 soil axial stress curve (penetration depth is 9 m) |
不同贯入深度对应的时间和速率如图 5所示。贯入时间随着贯入深度的增加而不断增长,贯入深度与贯入时间呈现出指数型规律,与Viking[6]的试验研究结果一致。
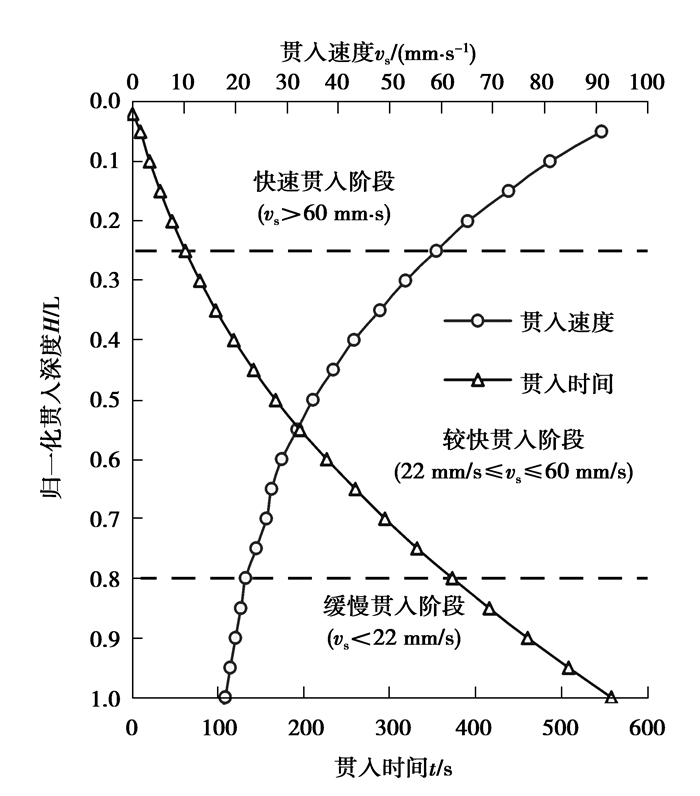
|
图 5 贯入速率分析 Figure 5 Penetration rate analysis |
Rao[13]根据桩的贯入速率,将桩的振动贯入过程分为快速贯入阶段、较快贯入阶段和缓慢贯入阶段,如表 2所示。从图 5可看出,管桩贯入初期,管桩贯入阻力小,管桩贯入速率沿贯入深度基本呈线性增长,管桩处于快速贯入阶段;当管桩贯入至0.25L处时,管桩贯入阻力明显增大,管桩从快速贯入阶段过渡到较快贯入阶段;当管桩贯入至0.8L处时,管桩从快速贯入阶段过渡到缓慢贯入阶段。
| 表 2 贯入速率 Table 2 Classification of penetration rate |
不同贯入阶段沉桩效率如表 3所示,由表可知,1)管桩振动贯入过程中,贯入总时间主要是由较快贯入阶段和缓慢贯入阶段控制;2)快速贯入阶段的贯入时间为总贯入时间的11%,但该阶段的贯入深度占总贯入深度的25%。进一步研究表明,快速贯入阶段平均贯入速率分别为较快贯入阶段、缓慢贯入阶段的2.3倍和3.8倍。由此可知,快速贯入阶段的沉桩效率明显高于较快贯入阶段和缓慢贯入阶段。
| 表 3 不同贯入阶段沉桩效率 |
许多学者开展了土体参数、桩型参数、振动频率和振动幅值对振动沉桩贯入速率影响的研究。Wong等[14]通过大比尺试验定量分析了沉桩阻力随砂土颗粒粒度、相对密实度的变化规律。Wang[15]和Lee[11]研究了桩的类型、形状、尺寸对贯入速率的影响。Whenham[16]基于大量试验数据,分析了桩、土等参数对振动沉桩性能的影响。Ghahramani[17]研究发现,存在最优振动频率,即桩在某一振动频率作用时,桩的贯入阻力显著减小,桩达到最大贯入速率。Denies[18]认为振动幅值对砂土中桩侧摩阻力影响是有限的,对于粘性土而言,当振动幅值超过临界值时,桩土间的粘聚力显著下降。
理论上增大静态荷载F0或动力荷载幅值Fc,将提高振动锤的激振力Fd,从而增加管桩的贯入速率。进一步研究静态荷载F0与动力荷载幅值Fc对贯入速率的耦合作用。
图 6给出了不同静载力与动载力比值F0/ Fc时的管桩贯入速率曲线。当静载力与动载力比值F0/Fc从0.04增长到0.44时,管桩贯入速率随着F0/Fc的增大而增大;当静载力与动载力比值F0/Fc=0.64时,管桩贯入速率开始减小,且贯入速率衰减速率增大;当静载力与动载力比值F0/Fc=0.84时,管桩贯入速率继续降低,导致管桩不能贯入至指定深度。因此,可以预测静载力与动载力比值F0/Fc在0.44~0.64之间存在一最优值,使得管桩贯入速率达到最大。
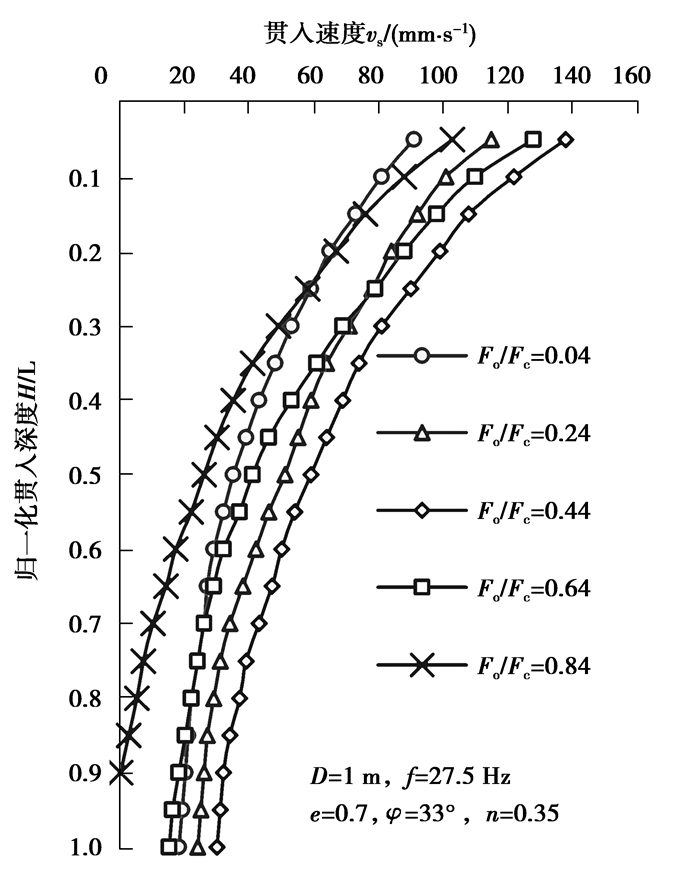
|
图 6 不同静载力与动载力比值时贯入速率曲线 Figure 6 Penetration rate curves at different F0/Fc |
进一步研究发现,当F0/Fc=0.5时,贯入速率达到峰值,即F0/Fc=0.5为最优值,如图 7所示。当0<F0/Fc≤0.5时,相同贯入深度处贯入速率随着F0/Fc的增大而增大;当F0/Fc>0.5时,相同贯入深度处贯入速率随着F0/Fc的增大而减小,甚至不能贯入至指定深度。

|
图 7 不同深度处贯入速率随静载力与动载力比值的变化 Figure 7 Variations of F0/Fc at different depth |
通过管桩的运动形式曲线(如图 8所示),可以解释F0/Fc存在最优值的现象。当0<F0/Fc≤0.5时,管桩在1个循环周期内的向上位移幅值zu等于向下位移幅值zd,此时,管桩上下反复运动的位移足够大,管桩能够与土体产生充分的剪切,降低侧摩阻力,提高贯入速率;当F0/Fc>0.5时,静载力F0超过动力荷载幅值Fc的一半,导致管桩回程时的上拔力不足,管桩在1个循环周期内的向上位移幅值zu小于向下位移幅值zd,且随着F0/Fc值的增大,管桩的向上振动运动逐渐减弱,管桩从高频振动贯入逐渐退化为静压贯入,导致贯入速率降低。
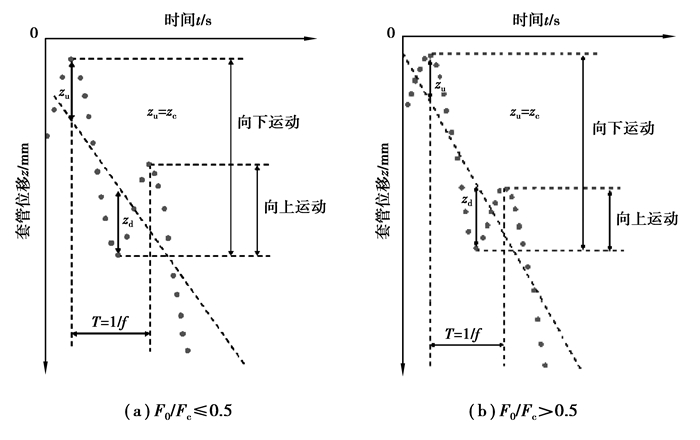
|
图 8 管桩运动形式曲线 Figure 8 Pipe pile movement form curve |
采用高频振动锤贯入管桩时,不能简单地认为通过增大静态荷载F0或动力荷载幅值Fc,就能够提高管桩贯入速率,应考虑到静态荷载F0与动力荷载幅值Fc的耦合关系,确保F0/Fc在0~0.5的范围内。
4 结论1) 管侧土体随着管桩的运动产生循环反复的剪切应力,管侧土体剪应力剪应变滞回曲线为典型的“香蕉”形,每个循环的滞回曲线均由2个剪胀阶段和2个剪缩阶段组成,能直观地反映出管壁与土体间的反复剪切作用。管端土体在管桩的作用下处于循环反复的加卸载状态,管端土体轴向应力剪应变滞回曲线为典型的“镰刀”形,管端土体经历2个显著的压缩阶段和拉伸阶段。
2) 管桩振动贯入过程中,贯入总时间主要是由较快贯入阶段和缓慢贯入阶段控制,而快速贯入阶段的沉桩效率明显高于较快贯入阶段和缓慢贯入阶段。
3) 采用高频振动锤贯入管桩时,不能简单地认为通过增大静态荷载F0或动力荷载幅值Fc,就能够提高管桩贯入速率,应该考虑到静态荷载F0与动力荷载幅值Fc的耦合关系,确保F0/Fc在0~0.5的范围内。
| [1] |
陈福全, 汪金卫, 李大勇, 等. 高频液压振动锤打桩的应用概况与研究进展[J]. 岩土工程学报, 2011, 33(S2): 224-231. CHEN Fuquan, WANG Jinwei, LI Dayong, et al. Application and advance of vibratory driving techniques using high-frequency hydraulic vibratory hammer[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S2): 224-231. (in Chinese) |
| [2] |
肖勇杰, 许万强, 陈福全. 全套管大直径振动取土灌注桩施工新技术[J]. 施工技术, 2015, 44(1): 61-64. XIAO Yongjie, XU Wanqiang, CHEN Fuquan. A new construction technology of large diameter cast-in-place piles with sleeves driven by vibratory hammers[J]. Construction Technology, 2015, 44(1): 61-64. (in Chinese) |
| [3] |
Holeyman A. An analytical model based computer program to evaluate the penetration speed of vibratory driven sheet piles[J]. Geotechnique, 1993, 43(18): 65-78. |
| [4] |
Vanden J F.Sand strength degradation within the framework of vibratory pile driving[D]. Louvain: Université Catolique De Louvain, 2001.
|
| [5] |
Salgado R, Loukidis D, Abou J G, et al. The role of soil stiffness non-linearity in 1D pile driving simulations[J]. Geotechnique, 2015, 65(3): 169-187. DOI:10.1680/geot.13.P.124 |
| [6] |
Viking K.Vibro-driveability-a field study of vibratory driven sheet piles in non-cohesive soils[D]. Stockholm: Royal Institute of Technology, 2002.
|
| [7] |
王伟.振动沉桩动力学分析和试验研究[D].石家庄: 河北科技大学, 2012. WANG Wei.Dynamic analysis and experimental study of vibrating pile sinking[D].Shijiazhuang: Hebei University of Science and Technology, 2012.(in Chinese) |
| [8] |
肖勇杰, 陈福全, 林良庆. 灌注桩套管高频振动贯入过程中挤土效应研究[J]. 岩土力学, 2015, 36(11): 3268-3274. XIAO Yongjie, CHEN Fuquan, LIN Liangqing. Study of squeezing effect due to sleeve for cast-in-place piles installation using high frequency vibratory hammers[J]. Rock and Soil Mechanics, 2015, 36(11): 3268-3274. (in Chinese) |
| [9] |
Helwany S. Applied soil mechanics with ABAQUS applications[M]. New Jersey: John Wiley & Sons, 2007.
|
| [10] |
Ekanayake S, Liyanapathirana D, Leo C. Influence zone around a closed-ended pile during vibratory driving[J]. Soil Dynamics and Earthquake Engineering, 2013, 53: 26-36. DOI:10.1016/j.soildyn.2013.06.005 |
| [11] |
Lee S H, Kim B I, Han J T. Prediction of penetration rate of sheet pile installed in sand by vibratory pile driver[J]. KSCE Journal of Civil Engineering, 2012, 16(3): 316-324. DOI:10.1007/s12205-012-1317-y |
| [12] |
Cudmani R, Sturm H. An investigation of the tip resistance in granular and soft soils during static, alternating and dynamic penetration[C]//International symposium on vibratory pile driving and on deep soil vibratory compaction, Paris, IEEE, 2006: 221-231.
|
| [13] |
Rao P M.Effect of pile geometry and soil saturation on the behavior of nondisplacement piles installed by vibration[D].Texas: University of Houston, 1993.
|
| [14] |
Wong D, Oneill M W, Vipulanandan C. Modelling of vibratory pile driving in sand[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1992, 16(3): 189-210. DOI:10.1002/(ISSN)1096-9853 |
| [15] |
Wang H K.Experimental study and finite element analysis of driveability and static behavior of various piles installed by vibratory driving[D]. Texas: Faculty of the Department of Civil and Environmental Engineering, University of Houston, 1994.
|
| [16] |
Whenham V.Power transfer and vibrator-pile-soil interactions within the framework of vibratory pile driving[D]. Louvain: Université Catholique De Louvain, 2011.
|
| [17] |
Ghahramani A.Vibratory pile driving uitimate penetration and bearing capacity[D]. Princeton: Princeton University, 1967.
|
| [18] |
Denies N, Canou J, Roux J N, et al. Sphere penetration experiments in vertically vibrated sand[C]//Proceedings of the fifth International Conference on Recent Advances in Geotechnical Earthquake Enginering and Soil Dynamics, San Diego, IEEE, 2010: 12-23.
|
 2018, Vol. 41
2018, Vol. 41


